| Issue |
JNWPU
Volume 38, Number 4, August 2020
|
|
|---|---|---|
| Page(s) | 755 - 765 | |
| DOI | https://doi.org/10.1051/jnwpu/20203840755 | |
| Published online | 06 October 2020 | |
Analyzing of Cooperative Locating Error and Formation Configuration of AUV Based on Geometric Interpretation
基于几何解释的集群AUV协同定位误差及编队构型分析
1
School of Marine Engineering, Northwestern Polytechnical University, Xi'an 710072, China
2
State Key Laboratory of Deep-Sea Manned Vehicles, China Ship Scientific Research Center, Wuxi 214082, China
Received:
29
July
2019
Because the evaluation of the location performance of AUVs with the lower bound of the Cramer-Rao inequality is not intuitive, the geometric interpretation method is proposed based on geometric ellipse. The Fisher information matrix is used to replace the Cramer-Rao inequality. The priori information matrix and the measurement information matrix are synthesized into the posterior information matrix through singular value decomposition. The geometric ellipse is used to geometrically represent the posterior information matrix. The posterior information ellipse area is used to establish the location performance evaluation function. By analyzing the performance evaluation function, the optimal formation configurations of single-master, dual-master and three-master AUVs are designed. The implementation of the special formation configuration for the three-master AUV formation proposed in the paper is easier, while the location performance of the optimal formation configuration is not much inferior. The simulation results verify that the optimal formation configuration has a higher location accuracy and that the special formation configuration is effective.
摘要
针对利用Cramer-Rao不等式下界评价集群AUV定位性能不直观的问题,基于几何椭圆提出了定位性能评价标准的几何解释方法。利用Fisher信息矩阵代替Cramer-Rao不等式,通过奇异值分解将先验信息矩阵与量测信息矩阵合成为后验信息矩阵,并利用椭圆对其进行几何表示,基于后验信息椭圆面积建立定位性能评价函数。通过分析性能评价函数,设计了单主、双主以及三主AUV集群的最优编队构型,并对三主AUV集群编队提出了特殊编队构型,其较最优编队构型的定位性能相差不大的情况下,更容易实现。仿真实验验证了最优编队构型具有更高的定位精度以及特殊编队构型的有效性。
Key words: autonomous underwater vehicles / information ellipse / cooperative location / formation configuration / location performance
关键字 : 集群AUV / 信息椭圆 / 协同定位 / 编队构型 / 定位性能
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
集群AUV协作系统执行能力和执行效率的显著提升, 都建立在AUV自身的精确定位基础之上。为了提高AUV的定位精度, 近年来, 利用AUV间的相对距离信息, 实现集群AUV的协同定位, 成为协同导航定位的重要研究方向[1-2]。
目前, 基于距离量测的协同导航定位技术的研究, 主要关注于定位算法的设计。张立川和杨建等[3-4]分别基于扩展卡尔曼滤波与容积卡尔曼滤波理论研究了多AUV协同导航定位算法, 主要融合内部和外部传感器信息, 并且显著提高集群中AUV的导航定位精度。文献[5]通过研究集群AUV协作系统的可观测性表明, 若系统可观测, 可以有效利用量测信息进行协同定位, 若不可观测, 协同定位误差将趋于发散。文献[6-8]研究表明通过改变控制输入(设计复杂航行路径)可增加系统的可观测性, 进而提高定位精度。文献[9]在可观测性分析的基础上, 对单主AUV编队进行可观测度分析, 研究表明控制相邻两时刻主从AUV之间角度的变化量, 可以提高协同定位系统的可观测度, 进而提高协同定位精度。
除此之外, 集群AUV的编队构型与定位性能的关系被少数学者所研究。AUV的定位过程可以看作是状态预测过程, 利用预测状态的协方差阵评价协同定位性能的优劣, Cramer-Rao不等式下界(CRLB, 其下界的倒数为Fisher信息量)从理论上给出了未知参数无偏估计的协方差矩阵下界, 文献[10]在未考虑先验信息的情况下, 利用此理论建立与编队构型参数有关的定位性能评价函数, 并得出双主AUV的最优编队构型。文献[11]将先验信息考虑在性能评价函数中, 对单主以及双主AUV的最优队形进行了讨论; 提出利用误差椭圆代替后验协方差阵, 并选取误差椭圆面积建立性能评价函数的思想, 但是没有对误差椭圆和融合观测量信息过程进行详细说明与几何解释, 实质依旧利用协方差矩阵的行列式建立性能评价函数。文献[12]研究了最优编队构型的敏感性问题。当集群AUV以最优编队构型进行运动时, 较小的角度值偏差不会对定位性能产生明显的影响。
可以看出, 对于评价协同定位性能的研究, 主要基于协方差阵建立的性能评价函数进行分析, 通过性能评价函数的最大化得到最优编队构型, 从而实现定位误差最小化。虽然此方法可以应用于评价定位误差优劣以及设计编队构型, 但是不能直观理解协同定位误差变化, 也不能作为编队构型的直观设计工具。针对这一问题, 本文基于CRLB/Fisher信息量对协同定位过程的误差变化进行了几何解释, 详细阐述了协方差阵转化为信息椭圆的过程, 基于信息椭圆解释了观测量对先验误差的影响, 分析得出集群AUV协同定位过程最优量测信息来源。除此之外, 本文以信息椭圆面积为基础, 建立性能评价函数, 对单主、双主以及三主集群AUV编队构型进行了深入研究, 并对相应编队构型的定位系统性能进行几何解释以及实验仿真分析。
1 基于距离量测的集群AUV协同定位系统
2 基于距离量测的协同定位原理
基于距离量测的协同定位方法是近年来发展起来的一种定位技术, 通过量测主从AUV之间相对距离信息对自身航位推算的状态信息进行修正, 原理如图1所示。协同定位系统中主AUV配备高精度惯性导航系统, 可以实现精确定位, 从AUV配备低精度航位推算系统、GPS与水声通信设备。为实现协同导航定位, 集群AUV协同定位系统往往配备一艘或几艘主AUV。执行任务前, 主、从AUV利用GPS进行时钟同步, 确保量测信息准确性; 航行过程中, 主AUV周期性发射声脉冲信号, 从AUV利用此信号解算两者相对位置, 并融合主AUV位置信息进行协同定位对从AUV位置误差进行校正。
图1为基于距离量测的协同导航定位原理示意图, 图中几何椭圆表示AUV的位置误差。当从AUV与主AUV进行距离量测后, 从AUV对自身的位置误差进行协同校正, 使得自身位置的不确定性减小。
对于在水中稳态航行的AUV而言, 求解其位置信息是一个三维问题。然而深度信息可以通过压力传感器精确测量, 并且AUV的俯仰角与横滚角变化较小, 进而将三维问题转化为二维问题。对于二维平面定位问题, 一般至少需要2个量测量确定从AUV的位置。对于多主AUV的协同定位系统, 已经满足2个量测量的要求, 但是对于单主AUV, 要满足此要求, 主要依据移动矢径原理并利用相邻两时刻的量测信息进行协同定位, 原理如图2所示。
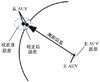 |
图1 基于距离量测的协同定位原理 |
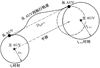 |
图2 基于移动矢径的协同定位原理 |
3 系统模型
建立从AUV的二维运动学方程
式中, uk, φk与Δt分别为从AUV在k时刻的前向航速、航向角与航位推算的采样时间。前向航速与航向角均受高斯白噪声干扰, 且系统噪声方差阵为Qk=diag[σμk2, σφk2]。
进而将从AUV的二维运动学方程进行简写
式中:xk=(xk, yk, φk)T为状态向量;f为非线性状态方程函数;uk=(uk, φk)T为输入向量;wk表示k时刻从AUV的过程噪声序列为高斯白噪声;Gk是过程噪声驱动矩阵。
建立主、从AUV的距离量测方程为
式中,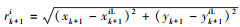 , 为k+1时刻第i个主AUV与从AUV的量测信息, i=1, …, m。其中上标iL表示第i个主AUV, vk为从AUV的量测噪声序列为高斯白噪声, Nk为量测噪声矩阵, h为非线性量测方程函数。
, 为k+1时刻第i个主AUV与从AUV的量测信息, i=1, …, m。其中上标iL表示第i个主AUV, vk为从AUV的量测噪声序列为高斯白噪声, Nk为量测噪声矩阵, h为非线性量测方程函数。
当i=1时, 即单主AUV协同定位系统, 量测距离信息为相邻两时刻的量测信息, 具体为
式中:rk与rk+1为相邻时刻量测量;Dxk, k+1与Dyk, k+1为从AUV由k至k+1时刻的移动矢径。
4 基于扩展卡尔曼的协同导航算法
集群AUV协作系统为非线性系统, 必须首先利用泰勒级数展开为线性系统, 随后利用卡尔曼滤波算法进行AUV状态的最优估计, 即为扩展卡尔曼的协同导航算法。具体步骤为:
状态一步预测
一步预测协方差阵
式中: Qk为系统噪声方差阵; Fk, k+1表示f关于xk的雅可比矩阵, 为f关于xk在点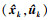 处的偏导数; Ck, k+1表示f关于uk的雅可比矩阵, 表示f关于uk在点
处的偏导数; Ck, k+1表示f关于uk的雅可比矩阵, 表示f关于uk在点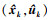 处的偏导数, 两者表示为
处的偏导数, 两者表示为
滤波增益矩阵
式中:Rk+1为量测噪声方差阵;Hk+1为距离量测方程的雅克比矩阵, 表示为
式中,θk+1i为k+1时刻第i个主AUV与从AUV的夹角。
单主AUV协同定位时, 利用相邻两时刻距离量测信息, 类比于从AUV与双主AUV的量测信息。对于量测方程的雅克比矩阵, 利用相邻两时刻从AUV与主AUV的夹角信息取代从AUV与双主AUV的夹角信息即可, 表示为
式中,θk与θk+1为相邻两时刻主从AUV的夹角, 分别取代了θk+11与θk+12。
状态与协方差阵更新为
通过(5)~(13)式, 对从AUV的状态信息进行最优估计。其中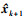 为协同定位估计的状态信息, Pk+1为衡量利用算法估计出的状态信息精度。为了更清楚地理解位置状态信息精度, 将(9)式代入(13)式, 并求逆可得
为协同定位估计的状态信息, Pk+1为衡量利用算法估计出的状态信息精度。为了更清楚地理解位置状态信息精度, 将(9)式代入(13)式, 并求逆可得
将(14)式利用Fisher信息矩阵表示
式中:Jk+1为后验信息矩阵;Jk, k+1为先验信息矩阵;Jk+1H为信息增益矩阵, 是对先验信息矩阵的修正。
对于位置状态信息的精度, 本文利用D-最优标准衡量, 即后验信息矩阵的行列式最大时, 定位性能最优
5 几何解释理论基础
6 信息椭圆
本文在考虑协方差阵时, 只考虑状态量x与y的误差, 并且其为正定矩阵。因而对于(15)式中信息矩阵, 可利用信息椭圆对其进行几何解释。本文以后验信息矩阵为例, 对其信息椭圆进行说明。首先为了方便, 可以将后验信息矩阵转化为对角阵
式中:a与b为后验信息矩阵的特征值(a>b);Pϕ为特征向量组成的旋转矩阵, 其定义为
因而, 定义后验信息椭圆为E(a, b, ϕ), a与b为椭圆长短轴参数, ϕ为旋转角, 具体如图3所示。
由于信息椭圆参数求解较为繁琐, 因而本文给出信息椭圆的长半轴、短半轴以及旋转角的直接计算形式。若后验信息矩阵如(19)式所示
则椭圆长短轴参数和椭圆长轴与x轴的夹角a, b, ϕ为
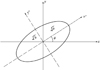 |
图3 后验信息椭圆示意图 |
7 协同定位误差的几何解释
由2.1节分析, 可以求得先验信息椭圆E1(a′, b′, ϕ′)与信息增益椭圆E2(μ, η, θ)的所有参数。进而可将(15)式利用椭圆参数表示为
对于后验信息椭圆参数, 可根据矩阵的奇异值分解得到, 具体为
式中:A=0.5(a′+b′+μ+η);B=(a′-b′)+(μ-η)cos(2(θ-ϕ′));C=(μ-η)·sin(2(θ-ϕ′))。
进而协同定位误差的几何解释, 如图4所示。
图4中点划线为信息增益椭圆, 虚线为先验信息椭圆, 实线为前两者合成的后验信息椭圆。对于D-最优标准而言, 后验信息椭圆面积越大, 定位性能越优, 进而可直观从后验信息椭圆面积确定协同定位性能的优劣, 并且从增加量可确定量测信息的优劣。根据(21)与(22)式对后验信息椭圆的面积进行分析, 为了简化分析, 定义其如(23)式所示
在先验条件已知的条件下, 根据(23)式可对观测信息进行选择或者对集群AUV的编队构型进行规划, 使得观测信息最优, 即确定角ϑ与椭圆面积S之间的关系, 最终使得估计状态信息最优。
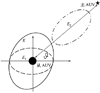 |
图4 协同定位误差的几何解释 |
8 集群AUV协同定位误差的几何解释及编队构型分析
根据(14)式可知, 后验信息矩阵由先验信息矩阵与信息增益矩阵组成, 然而根据(6)式可知, 先验信息由此时刻之前的所有后验信息和此时刻的状态信息组成, 难以确定具体的形式。为了更好地分析, 对后验信息矩阵进行简化, 其中R为量测噪声, 一般取常值, 可以忽略不计[13-14], 进而后验信息矩阵可定义为
根据(10)式, 可以得到
可根据(20)式, 求出若干主AUV的后验信息椭圆参数a, b与ϕ, 并进行几何解释。并根据(23)式, 定义协同定位性能的评价标准
9 单主AUV的协同定位分析
根据第一节分析可知, 对于基于距离量测的单主AUV协同定位系统, 从AUV主要通过移动矢径原理, 使用相邻两时刻量测信息对位置误差进行修正。结合(11)式与(25)式, 可以得到单主AUV协同定位的后验信息矩阵表达式为
进而根据(20)式可得到后验信息椭圆E(a, b, ϕ)的所有参数: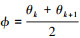 , a=2+2|cos(θk-θk+1)|, b=2-2|cos(θk-θk+1)|。
, a=2+2|cos(θk-θk+1)|, b=2-2|cos(θk-θk+1)|。
进而根据(26)式, 可定义单主AUV协同定位系统的性能评价标准为
进而对单主AUV协同定位系统的后验信息矩阵进行几何说明。对于椭圆面积而言, 若长轴与短轴的和为定值时, 当且仅当长轴与短轴相等时, 椭圆面积最大, 即性能指标Γ1最大。即2+2|cos(θk-θk+1)|=2-2|cos(θk-θk+1)|时, 定位性能最优, 信息椭圆的几何形状为圆。考虑到实际情况, 因此可得当θk-θk+1=±90o时, 定位性能最优, Γ1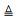 ab=4, 最优编队构型如图5所示, 几何解释如图6所示。图6中虚线表示后验信息椭圆, 实线表示最优后验信息椭圆。当量测信息最优时, 其几何形状变为半径为2的圆。为了证明几何分析的正确性, 对(28)式进行仿真, 取θk, θk+1∈[-180°, 180°], 如图7所示。由图7可知, 当相邻两时刻的量测夹角差的绝对值越接近90°, 定位性能越优, 反之, 定位性能越差。当相邻两时刻的量测夹角绝对值为90°时, 椭圆面积最大, 定位性能最优, 当相邻两时刻的量测夹角差为0°或±180°时, 椭圆面积最小, 定位性能最差。此分析结果与文献[9]基于可观测度分析结果一致, 即随着协同定位系统的可观测度越大, 定位性能越优, 并且当定位性能最差时, 相当于主从AUV的航行路径为不可观测路径, 从侧面证明了性能评价函数的正确性。
ab=4, 最优编队构型如图5所示, 几何解释如图6所示。图6中虚线表示后验信息椭圆, 实线表示最优后验信息椭圆。当量测信息最优时, 其几何形状变为半径为2的圆。为了证明几何分析的正确性, 对(28)式进行仿真, 取θk, θk+1∈[-180°, 180°], 如图7所示。由图7可知, 当相邻两时刻的量测夹角差的绝对值越接近90°, 定位性能越优, 反之, 定位性能越差。当相邻两时刻的量测夹角绝对值为90°时, 椭圆面积最大, 定位性能最优, 当相邻两时刻的量测夹角差为0°或±180°时, 椭圆面积最小, 定位性能最差。此分析结果与文献[9]基于可观测度分析结果一致, 即随着协同定位系统的可观测度越大, 定位性能越优, 并且当定位性能最差时, 相当于主从AUV的航行路径为不可观测路径, 从侧面证明了性能评价函数的正确性。
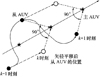 |
图5 单主AUV协同定位最优编队构型 |
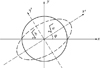 |
图6 单主AUV最优协同定位系统几何解释示意图 |
 |
图7 单主AUV协同定位性能评价仿真示意图 |
10 多主AUV集群的协同定位分析
对于二维平面的AUV协同定位, 从AUV仅使用单一时刻的量测信息不能进行状态预测, 至少需要2个量测信息对其位置进行无偏估计。此外, 已有研究表明在一定程度上, 主AUV数量的增加可以抑制协同定位误差的增长[15-16]。因此, 在设计协同定位系统时, 往往利用多主AUV达到状态预测的要求。根据1.3节的分析, 对于双主AUV的距离量测方程的雅克比矩阵, 只需要将从AUV与单主AUV相邻两时刻的量测信息转换成从AUV与双主AUV的量测信息, 双主AUV与单主AUV协同定位分析过程及结论一致, 此处不再进行推导。但是实际中, 单主AUV需要设计复杂的航行路径, 使从AUV的状态预测性能更优, 但是一般不能达到最优解。而对于双主AUV只需通过设计编队构型, 即可达到理论分析的最优解。本节主要讨论在2个量测信息基础上, 融合第3个量测信息的协同定位系统, 即对三主AUV集群协同定位误差进行几何解释与编队构型进行研究。
本文认为使用2个观测量的量测信息矩阵为先验量测信息, 当第3个量测信息被引入协同定位系统时, 其为后验量测信息。因而根据(24)式, 三主AUV协同定位的后验信息矩阵表示为
进而后验信息矩阵利用几何椭圆表示为
进而根据(22)式可得到三主AUV协同定位系统的后验信息椭圆E(a, b, ϕ)的特征值为
式中, θ1, θ2与θ3分别为三主AUV与从AUV的夹角, 并且对于后验量测信息椭圆而言, 椭圆短半轴为0, 定义为退化信息椭圆[17], 只能提供一个方向的信息量, 为实现后验信息椭圆面积最大化, 确定退化信息椭圆方向尤为重要。
根据(26)式, 定义三主AUV集群协同定位系统的性能评价标准为
对三主AUV集群协同定位系统的后验信息矩阵进行几何说明, 令其长轴与短轴相等, 椭圆面积最大, 即性能指标Γ3最大。求得三主AUV的最优量测信息角, 如表 1所示。
最优量测信息角
表 1中ϑ1,ϑ2与ϑ3分别为三主AUV的量测信息夹角, 定义为ϑ1=θ1-θ2, ϑ2=θ1-θ3, ϑ3=θ2-θ3并且ϑ1+ϑ2+ϑ3=360°。
对于此4种最优位置状态, 考虑实际情况, 后3种可归属为同一种编队构型。因此, 三主AUV集群协同定位系统最优的编队构型有2种, 如图8至9所示, 几何解释如图10所示。
图10中虚线表示先验量测信息椭圆, 实线表示最优后验信息椭圆。从图中可以看出, 此种情况相当于第3个观测量只使得先验量测信息椭圆的短轴增加, 而长半轴没有变化, 使其几何形状变为半径为3的圆。
此外, 对于(31)式及ϑ1+ϑ2+ϑ3=360°而言, 倘若3个主AUV中有2个主AUV的夹角差绝对值为90°时, 性能评价函数为恒值, Γ3 8, 几何解释如图11所示。
8, 几何解释如图11所示。
图11中虚线为表示最优的先验量测信息椭圆, 即3个主AUV中有2个主AUV的夹角差绝对值为90°, 其几何形状是半径为2的圆, 相当于双主AUV最优协同定位系统的后验信息椭圆。实线表示特殊编队构型的后验信息椭圆, 从图中可以看出, 其几何形状的一个方向的轴增加变为椭圆。对于圆形而言, 所有方向的轴长相等, 无论任何方向轴长增加, 其面积增加量将一致, 因此从几何角度证明了理论分析的正确性。
为了对此恒值Γ3 8, 更深入理解, 本文分2种实际情况进行讨论:
8, 更深入理解, 本文分2种实际情况进行讨论:
第1种:若2个主AUV的夹角绝对值已为90°, 在确定第3个主AUV在协同定位系统中的位置时, 则可以忽略具体位置, 只需考虑AUV之间避障, 从AUV的位置状态预测性能将一致。此情况的编队构型如图12所示。
第2种:若2个主AUV的夹角为任意值时, 在确定第3个主AUV在协同定位系统中的位置时, 只需使其与其他任意一个主AUV的夹角绝对值为90°, 从AUV的状态预测性能将达到一个较优的状态。此情况的编队构型如图13所示。
为了证明几何分析的正确性, 对(31)式进行仿真。根据(31)式可知, 椭圆面积只与两两主AUV的量测信息的夹角绝对值有关, 因此当定义一个主AUV与从AUV的夹角时, 对椭圆面积的评价函数没有影响。本文假定从AUV在原点, 主AUV1相对于从AUV的夹角θ1=10°时, 主AUV2与主AUV3相对于从AUV的夹角分别取θ2, θ3∈[0°, 360°], 仿真结果如图14至15所示。
由图14和15可知, 椭圆面积最大值为9, 最小值为0。当椭圆面积最大时, 位置状态预测性能最优, 如图15中黑点所示, 共有8个点, 代表 3个主AUV的8种不同位置状态, 具体如表 2所示。
最优位置状态
根据表 2的8种不同位置状态可知, 其与表 1分析的4种最优量测信息角相对应, 都对应着图8至9中2种编队构型, 验证了上文分析的正确性。
当椭圆面积最小时, 此位置状态预测性能最差, 如图15中菱形点所示, 共有4个点, 代表了3个主AUV 4种不同的位置状态, 具体如表 3所示。
最差位置状态
根据表 3中3个AUV的位置状况可知, 当三主AUV与从AUV的航行路径为同一直线时, 从AUV的预测位置状态将最差, 此情况类比于单主AUV的不可观测路径, 实际航行时, 应该避免此类编队构型。
对于3.2节分析的特殊情况,如图15中4条虚线所示, 其直线表达式分别为θ2=100°, θ2=280°, θ3=100°与θ3=280°, 椭圆面积恒为8。此4条虚线表示的实际情况为:对于基于三主AUV集群协同定位系统而言, 任意两主AUV的量测信息夹角差的绝对值为90°时, 无需考虑第3个领航艇的位置, 其椭圆面积始终为8。此情况较三主AUV的最优情况椭圆面积虽有减少, 但是此特殊情况只需要保证协同定位系统中的一个夹角差为90°, 较最优的编队构型少确定2个夹角差, 因而此编队构型将更容易实现。
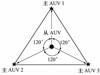 |
图8 三主AUV协同定位最优编队构型_1 |
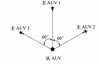 |
图9 三主AUV协同定位最优编队构型_2 |
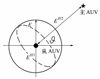 |
图10 三主AUV最优协同定位系统几何解释示意图 |
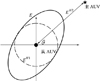 |
图11 三主AUV特殊协同定位系统几何解释示意图 |
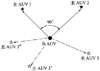 |
图12 三主AUV协同定位特殊编队构型_1 |
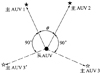 |
图13 三主AUV协同定位特殊编队构型_2 |
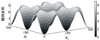 |
图14 三主AUV协同定位性能评价仿真示意图 |
 |
图15 三主AUV协同定位性能评价仿真平面图 |
11 数值仿真
基于扩展卡尔曼算法设计了3组仿真实验对不同状态的协同定位性能进行仿真比较分析。对于单主AUV与双主AUV可参考文献[9-11]对本文的理论结果进行验证。本节主要对三主AUV集群协同定位系统的理论分析结果进行仿真分析。
仿真过程中, 所有主、从AUV间的距离量测噪声为σr2=(5 m)2的零均值高斯白噪声; 从AUV的速度量测噪声为σu2=(0.4 m/s)2,与航向角量测噪声为σφ2=(2°)2的零均值高斯白噪声, 并且两者独立互不相关。采用蒙特卡洛法估算协同定位系统的从AUV的定位误差, 重复仿真计算100次, 取其统计平均值。
实验一 主AUV1、主AUV2、主AUV3与从AUV分别由(0, 500)m, (0, 1 000)m, (0, 1 500)m和(0, 0)m出发, 航向角均为90°并且沿同一直线航行, 航行速度均为2 m/s, 仿真实验的采样周期为1 s, 此情况为不可观测路径, 椭圆面积为0。图16给出了从AUV的航位推算与协同定位误差比较图, 协同定位误差随时间增大趋于发散, 协同导航算法失效。
实验二 三主AUV分别按照表 4的位置状态出发, 航向角均为90°并且沿平行直线航行, 航行速度均为2 m/s, 仿真实验的采样周期为1 s。并且表 4中给出了不同位置状态的椭圆面积及仿真后的平均定位误差。图17为主AUV在不同位置状态时, 从AUV的协同定位误差比较图。
三主AUV位置状态
根据表 4与图17可知, 随着椭圆面积的增大, 协同定位误差减小。
实验三 主AUV1、主AUV2、主AUV3与从AUV分别由(-707, 707)m, (707, 707)m, (0, 1 000)m和(0, 0)m出发, 航向角均为90°并且沿平行直线航行, 航行速度均为2 m/s, 仿真实验的采样周期为1 s。此情况的主AUV1与主AUV2的夹角为90°, 随后始终保持此两主AUV的位置不变, 通过改变主AUV3的位置, 使得其与另外两主AUV的夹角改变, 从而设置一系列实验, 验证理论分析正确性。表 5给出了主AUV3的不同位置状态, 椭圆面积及平均滤波误差值。图18给出了主AUV3在不同位置状态时, 从AUV的协同定位误差比较图。
主AUV3的不同位置状态
从表 5与图18中可以看出, 当两主AUV的量测信息夹角为90°时, AUV3位于不同位置时, 从AUV的协同定位误差基本一致。
因此, 在基于三主AUV集群协同定位时, 应避免不可观测路径, 并且可以通过本文中的后验信息椭圆面积计算公式(性能指标函数), 事先对协同定位误差有初步的了解。除此之外, 可以按照本文给出的最优编队构型设计AUV的具体位置, 并且在AUV的构型不能达到最优时, 给出了一种特殊情况, 只需要使2个主AUV的夹角差达到90°, 而不必考虑第3个主AUV的具体位置, 协同定位误差也能达到一个较优的等级, 但是其编队构型较最优编队构型更容易实现, 进而验证了理论分析的正确性。
 |
图16 从AUV定位误差图 |
 |
图17 从AUV定位误差图 |
 |
图18 从AUY定位误差图 |
12 结论
本文从Fisher信息矩阵角度研究了基于距离量测的集群AUV协同定位算法, 提出了协同定位误差的几何解释方法; 基于后验信息椭圆面积建立了编队构型的性能评价函数, 通过增大后验信息椭圆面积以降低协同定位误差, 从而估计最优的编队构型, 并指出当椭圆长短轴相等时, 编队构型最优。仿真结果表明, 通过最大化后验信息椭圆面积求取的最优编队构型, 相比其他编队构型, 定位性能有明显的提升。此外, 对于三主集群AUV协同定位系统, 以本文提出的特殊编队构型航行时, 定位性能较最优定位性能相差不大的情况下, 更容易实现。
References
- Liu Mingyong. Cooperative Navigation Technology for Underwater Vehicles[M]. Beijing:National Defence Industry Press, 2014:1-21 (in Chinese) [Google Scholar]
- Zhang Lichuan, Xu Shaofeng, Liu Mingyong, et al. Advances in Cooperative Navigation and Localization for Multi-UUV Systems[J]. Chinese High Technology Letters, 2016, 26(5): 475-482 [Article] (in Chinese) [Google Scholar]
- Zhang Lichuan, Xu Demin, Liu Mingyong, et al. Research on Cooperative Navigation of Multiple AUVs Using Moving Long Baseline[J]. Robot, 2009, 31(6): 581-585 [Article] (in Chinese) [Google Scholar]
- Yang Jian, Luo Tao, Wei Shile, et al. A Cooperation Localization Method of MUUVs Based on CKF[J]. Ship Electronic Engineering, 2018, 38(2): 53-57 [Article] (in Chinese) [Google Scholar]
- Papadopoulos G. Underwater Vehicle Localization Using Range Measurement[D]. Cambridge: Massachusetts Institute of Technology, 2010 [Google Scholar]
- Maurice F F, Papadopoulos G, John J L, et al. Cooperative AUV Navigation Using a Single Maneuvering Surface Craft[J]. The International Journal of Robotics Research, 2010, 29(12): 1461-1474 10.1177/0278364910380760 [CrossRef] [Google Scholar]
- Teck T Y, Chitre M. Single Beacon Cooperative Path Planning Using Cross-Entropy Method[C]//MTS/IEEE Oceans, Waikoloa, 2011: 1-6 [Google Scholar]
- Fang Xinpeng, Yan Weisheng, Li Junbing. An Effective Observability Analysis for the Leader-Follower Autonomous Underwater Vehicles(AUVs) Cooperative Localization Based on Range Measurements[J]. Journal of Northwestern Polytechnical University, 2012, 30(4): 547-552 [Article] (in Chinese) [Google Scholar]
- Xu Bo, Xiao Yongping, Gao Wei, et al. A Cooperative Navigation Approach and Its Verification of USVs with Leader[J]. Acta Armamentarii, 2014, 35(11): 1836-1845 [Article] (in Chinese) [Google Scholar]
- Ma Peng, Zhang Fubin, Xu Demin. Optimality Analysis for Formation of MAUV Cooperative Localization with Two Leaders Based on Range Measurements[J]. Control and Decision, 2018, 33(2): 256-262 [Article] (in Chinese) [Google Scholar]
- Fang Wang, Li Jianlong, Sun Chen. Study of Optimal Formations for AUV Cooperative Navigation with Range Measurements[J]. Control Engineering of China, 2018, 25(9): 1679-1685 [Article] (in Chinese) [Google Scholar]
- Fang Xinpeng, Yan Weisheng, Zhang Fubin, et al. Formation Geometry of Underwater Positioning Based on Multiple USV/AUV[J]. Systems Engineering and Electronics, 2014, 36(5): 947-951(in Chinese) [Google Scholar]
- Shen X, Varshney P K. Sensor Selection Based on Generalized Information Gain for Target Tracking in Large Sensor Networks[J]. IEEE Trans on Signal Processing, 2014, 62(2): 363-374 10.1109/TSP.2013.2289881 [CrossRef] [Google Scholar]
- Sonia Mart'lnez, Bullo F. On Optimal Sensor Placement and Motion Coordination for Target Tracking[J]. Automatica, 2006, 42(4): 661-668 10.1016/j.automatica.2005.12.018 [CrossRef] [Google Scholar]
- Roumeliotis S I, Rekleitis I M. Propagation of Uncertainty in Cooperative Multirobot Localization:Analysis and Experimental Results[J]. Autonomous Robots, 2004, 17(1): 41-54 10.1023/B:AURO.0000032937.98087.91 [CrossRef] [Google Scholar]
- Larsen T D, Andersen N A, Ravn O, et al. Incorporation of Time Delayed Measurements in a Discrete-Time Kalman Filter[C]//IEEE Conference on Decision & Control, Las Vegas, 2002 [Google Scholar]
- Win M Z, Shen Y, Wymeersch H. On the Position Error Bound in Cooperative Networks: a Geometric Approach[C]//IEEE International Symposium on Spread Spectrum Techniques & Applications Bologna, 2008 [Google Scholar]
All Tables
All Figures
 |
图1 基于距离量测的协同定位原理 |
| In the text | |
 |
图2 基于移动矢径的协同定位原理 |
| In the text | |
 |
图3 后验信息椭圆示意图 |
| In the text | |
 |
图4 协同定位误差的几何解释 |
| In the text | |
 |
图5 单主AUV协同定位最优编队构型 |
| In the text | |
 |
图6 单主AUV最优协同定位系统几何解释示意图 |
| In the text | |
 |
图7 单主AUV协同定位性能评价仿真示意图 |
| In the text | |
 |
图8 三主AUV协同定位最优编队构型_1 |
| In the text | |
 |
图9 三主AUV协同定位最优编队构型_2 |
| In the text | |
 |
图10 三主AUV最优协同定位系统几何解释示意图 |
| In the text | |
 |
图11 三主AUV特殊协同定位系统几何解释示意图 |
| In the text | |
 |
图12 三主AUV协同定位特殊编队构型_1 |
| In the text | |
 |
图13 三主AUV协同定位特殊编队构型_2 |
| In the text | |
 |
图14 三主AUV协同定位性能评价仿真示意图 |
| In the text | |
 |
图15 三主AUV协同定位性能评价仿真平面图 |
| In the text | |
 |
图16 从AUV定位误差图 |
| In the text | |
 |
图17 从AUV定位误差图 |
| In the text | |
 |
图18 从AUY定位误差图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


