Study on ultra short baseline positioning system based on improved quad array and extended Kalman filter

Xutao HE; Long XIE; Haining XU; Yuan LI; Lei ZHANG; Jianbo WANG

doi:10.1051/jnwpu/20254330592

All issues

Volume 43 / No 3 (June 2025)

JNWPU, 43 3 (2025) 592-599

Full HTML

Open Access

Issue		JNWPU Volume 43, Number 3, June 2025


Page(s)		592 - 599
DOI		https://doi.org/10.1051/jnwpu/20254330592
Published online		11 August 2025

JNWPU 2025, 43(3): 592–599

Study on ultra short baseline positioning system based on improved quad array and extended Kalman filter

基于改进四元基阵的超短基线定位系统研究

Xutao HE (何旭涛)¹^,2, Long XIE (谢龙)¹^,2, Haining XU (徐海宁)¹, Yuan LI (李渊)¹^,2, Lei ZHANG (张磊)¹^,2 and Jianbo WANG (王剑波)³

¹ State Grid Zhoushan Power Supply Company, Zhoushan 316021, China
² Zhejiang Zhoushan Marine Power Research Institute Co., Ltd., Zhoushan 316021, China
³ Shaanxi Hard Equipment Technology Co., Ltd., Xi'an 710086, China

Received: 21 November 2023

Abstract

Ultra-short baseline equipment has been widely used in underwater positioning because of its small size and flexible use. In order to eliminate the phase ambiguity in the long distance measurement of ultra-short baseline system, an improved four-element array is proposed, which solves the above-mentioned problem effectively and improves the positioning accuracy. At the same time, in order to improve the precision of the phase difference between the measured elements, the acoustic signal is denoised by using the extended Kalman filter. The simulation results show that comparing with the traditional matrix, the improved four-element matrix improves the positioning accuracy by nearly one order of magnitude, and effectively reduces the number of primitives comparing with the improved eight-element matrix.

摘要

超短基线设备由于尺寸小、使用灵活, 在水下定位时得到了广泛应用。为了消除超短基线系统长距离测距的相位模糊问题, 提出了一种改进传统的四元基阵, 有效地解决了相位模糊问题, 并提高了定位精度。同时, 为了提高测量的基元间相位差的精度, 通过扩展卡尔曼滤波对声波信号进行了降噪。仿真验证的结果表明, 相对于传统基阵, 改进的四元基阵将定位精度提升了将近一个数量级, 且相对于改进的八元基阵有效减小了基元数。

Key words: ultra short baseline system / underwater positioning / quaternion orthogonal array / extended Kalman filtering

关键字 : 超短基线系统 / 水下定位 / 四元正交基阵 / 扩展卡尔曼滤波

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

在水下环境进行作业时, 常需要对目标进行精确定位。然而，由于海洋等介质的性质, 电磁波信号会严重衰减，难以通过声波对水下物体进行定位, 相对于在空气中, 信号衰减较小。水声定位技术可以分为长基线(long base line, LBL)系统、短基线(short base line, SBL)系统和超短基线(ultra-short base line, USBL)系统[1]。相对于其他水声定位系统，超短基线系统有着体积小、灵活性高、操作方便的优点, 应用较为广泛。

然而, 超短基线系统在实际应用时, 往往会由于水下存在的各种噪声, 对水下物体的定位精度产生较大影响。为了提高水声系统的定位精度, 可以通过改进基阵, 提高采集的声波信号质量。文献[2]提出了一种新的八元基阵用于超短基线系统, 有效地解决了长程超短基线的相位模糊问题。文献[3]提出了一种基于平滑算法的交互多模型(IMM)算法, 并利用自适应鲁棒平方根容积卡尔曼滤波器提高了超短基线系统的深海定位精度。文献[4]针对海底噪声中的粗差, 采用抗差卡尔曼滤波有效地提高了超短基线系统的定位精度。本文主要对超短基线系统的基阵进行了改进, 为了减小基点之间相位差测量的误差, 提高了通过应答器所收声波信号的质量。文献[5-6]提高了相邻基元接收信号时延估计的精度。文献[7]将解模糊问题转化为对模糊数的分类识别, 对分类器的结果进行融合, 得到了无模糊观测条件。

水声定位系统的准确性不仅取决于基阵影响的定位精度, 还来自于安装基阵时对传感器自身和传感器之间的误差标定和修正。文献[8-11]分别对水声定位技术中的水下声速和声线弯曲进行了修正, 都较为有效地改善了定位系统的定位精度。文献[12]提出了一种小角度近似的超短基线安装误差标定算法, 并通过最小二乘法计算得到了安装误差, 较好地减小了定位系统误差。文献[13]通过一种改进的自适应卡尔曼滤波器, 将误差包含在校正模型中, 减小了系统误差对定位精度的影响。

本文提出了一种改进四元阵列的新型基阵, 有效地解决了超短基线系统进行长距离测量时产生的相位模糊问题, 同时有效提升了测量精度。为了保证相邻基元之间接收声波信号相位差的精度, 通过扩展卡尔曼滤波对声波信号进行了滤波。

1 超短基线水下定位技术

1.1 超短基线系统组成

水声定位系统是通过测定声波信号的传播时间或者不同声波信号的相位差来确定水下物体的位置。而超短基线具有结构简单、灵活性强、操作方便的优点。

超短基线系统由一个换能器、声学基阵以及水下应答器组成。其中换能器是将电信号转换成声信号对外发射声波信号, 应答器收到声波信号之后发射应答信号, 而声学基阵则是负责接收返回的声波信号[14]。

而在本文中, 因为要通过超短基线系统确定水下电缆的精确位置, 所以将应答器安装在水下电缆上, 而由换能器和声学基阵集成的声头则安装在带有GPS和姿态测量系统的船上。通过GPS和SINS组合定位确定船的精确位置[15], 由于它的定位精度较高, 本文不考虑定位误差。本文使用的超短基线水下定位技术示意图如图 1所示。

图1

超短基线水下定位系统的结构

1.2 超短基线定位原理

超短基线确定水下物体坐标的大致过程和长、短基线系统类似, 通过水下应答器和声头的斜距长度及其与以声头为原点的坐标系x, y, z轴夹角来计算水下应答器的坐标。其具体原理示意图如图 2所示。

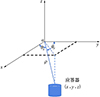图2

超短基线定位原理示意图

在图 2中, o为声头的中心, 同时其一般也是声学基阵的几何中心。在一般的工程中, 斜距ρ通过水下的声速和信号发出到收到之间的时延计算得到, 设时延为Δt, 水下的声速为c, 则斜距ρ的计算公式为

而θ_x和θ_y是斜距与x轴、y轴之间的夹角, 由于在水下中不方便测量, 通常通过测量信号到基阵中不同基元的相位差计算得到。水下物体的位置坐标可以表示为(x, y, z), 其计算公式为

由于高度的测量是通过水平测量的值计算得来的, 往往误差较大, 一般可以通过深度计来辅助测量[16]。因为超短基线基阵的尺寸很小, 所以可以近似其收到的声波信号为平行的。不同基元接收到声波信号的相位差如图 3所示。

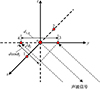图3

超短基线相位差示意图

由图 3可知, 基元3, 4之间的距离为d_{3, 4}=d, 设这一段水下声速为c, 声波到达同一坐标轴2个相邻基元的时间差为t, 则

设声波频率为f, 波长λ，则声速可以表示为

设ϕ为声波到达不同基元时的相位差，根据振动方程ϕ和频率f之间的关系, 时间差可以表示为

将c, t代入公式(3)中可得声波信号和坐标轴的夹角可以表示为

以基元1, 2为例分析传统超短基线系统的定位精度。基元1, 2接收信号的相位差ϕ_{1, 2}为

根据公式(7)可以得到目标x坐标的测量误差Δx为各个可能产生误差的部分求偏导之和

在只有ϕ_{1, 2}存在误差的情况下, x轴定位误差为

定位精度受到基元1, 2间距的限制, 最高为

因此，在未考虑其他误差的情况下, 当相位测量误差的单位为度时, 传统超短基线定位精度最高可达斜距的0.556%。这是传统超短基线阵面临的技术困难, 即由相位测量模糊导致系统的定位精度受到限制。

2 改进四元基阵超短基线定位系统

2.1 非等距四元基阵结构

针对传统超短基线定位精度低的问题, 采用阵形如图 4所示的八元超短基线阵解决传统超短基线定位精度低的问题。图 4所示八元阵是由2个十字正交的直线阵构成, 同轴上相邻最近的2个阵元间距d=0.4λ, 最大间距L=8d。通过采用同轴上最远的2个1, 4阵元和5, 8阵元对目标分别进行x轴及y轴方向的定位, 提高了定位精度。

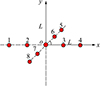图4

改进的八元基阵示意图

本文在此新型阵型的前提下进行改进, 减小了基元数量, 使得相邻基元不等距, 如图 5所示。

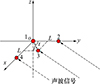图5

改进的四元基阵示意图

和八元基阵类似, 基元1, 2和基元1, 4之间的距离是基元1, 3之间的8倍, 即L=8l。由于基元1, 3之间的距离较短, 一般不会产生相位多值问题。假设基元1, 2或基元1, 4之间距离对应的相位差可以表示为2kπ+Δϕ₀, 其中k可以通过基元1, 3之间相位差确定, 具体的方法在下文中详细阐述。

2.2 改进四元阵列的位置解算

由公式(7)可以得到斜距ρ在x轴和在基元1, 3方向上的投影为:

由于基元1, 3之间的距离较短, 导致ϕ_{1, 3}不存在相位多值模糊。为了计算简便, 将声波信号投影到xoy平面上, 在这个平面上计算相位差和投影之间的关系。投影结果如图 6所示。

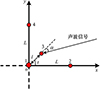图6

改进的四元基阵二维示意图

设基元1, 3和声波信号之间的夹角为α_{1, 3}, 则其在x, y轴上的投影相对于基元1, 4和基元1, 2的方位角分别为

x方向：有效间距d=l-cosπ/4, y方向：有效间距d=l-sinπ/4, 由公式(7)可得声波信号通过基元1, 3在x, y轴的相位差为

根据基元间的距离关系L=8l, 通过直接测量和间接计算得到α_{1, 2}≈α_{1, 3_x}, α_{1, 4}≈α_{1, 3_y}则声波信号分别通过基元1, 2和基元1, 4的相位差为

因为相位的测量区间为[-π, π], 所以当\begin{document}$\left|\phi_{1, 3_x}\right|>\frac{\pi}{8 \sqrt{2}}$\end{document}时, ϕ_{1, 2}即位于多值区间。此时ϕ_{1, 2}真实的测量值应该为

当ϕ_{1, 2}和\begin{document}$8 \sqrt{2} \phi_{1,3_x}$\end{document}的差值在[-π, π]之间时, 得到的ϕ_{1, 2}即为真实的测量值。这样, 便通过间接计算方式消除了相位多值模糊。

实际操作时可用(17)式对ϕ_{1, 2}和ϕ_{1, 4}进行相位补偿

公式(17)中, round( )为四舍五入取整运算, 此时ϕ_{1, 2_c}, ϕ_{1, 3_c}通过相位补偿后已无相位模糊问题。

因此, 在只有ϕ_{1, 2}存在误差的情况下, 根据新阵型的几何参数, 最高的定位精度为

同样, 对上述数值例子来说, 当相位测量误差的单位为度时, 在未考虑其他误差时, 新基阵定位精度最高能够达到斜距的0.069 5%, 定位精度改善程度与已有八元阵相同。

2.3 方位角度测量对相位误差影响分析

上述分析都是基于测量所得α_{1, 2}≈α_{1, 3_x}, α_{1, 4}≈α_{1, 3_y}无误差时的相位补偿, 对于角度α存在误差的情况分析如下。

当角度α存在Δα误差时, 由公式(15)可得

由三角关系变换, (19)式可变为

式中, α比较小, 所以sinα可以用α代替。

由公式(16)和公式(20)可得, 角度误差对基元3, 2间相位差影响为

由公式(22)可得\begin{document}$\bar{\phi}_{1, 2}$\end{document}额外相位差为

当Δα=1°时, 可得

由此可见, 在角度α存在误差Δα不大时, 通过公式(16)对基元1, 2进行相位补偿不会出现额外2π相位差模糊; 同理, 对基元3, 4也是一样的。

3 仿真验证

3.1 采样频率对定位精度的影响分析

采样频率相同时，不同的信噪比(SNR)会导致降噪效果不同；通常SNR越高，效果越好。但在系统噪声背景基本稳定的前提下，提升SNR需要相应增加发射功率。本文研究不同SNR下，系统的定位精度和信号处理所需时间。由此，可在维持特定噪声环境的条件下，为满足应用需求精度与时效配置最优发射功率提供依据。

本文将采样频率设置为2 kHz, 将信噪比(SNR)从16 dB调制至22 dB, 分别通过信号处理中常用的低通滤波器、自适应残差滤波和卡尔曼滤波在7个不同的采样频率下对信号进行降噪。本文在图 9中显示了3种方法在不同信噪比下的相位误差。

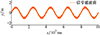图7

滤波前的声波信号

图8

滤波后的声波信号

图9

不同信噪比下不同方法相位误差

通过扩展卡尔曼滤波对声波信号进行降噪之后, 得到的声波信号如图 8所示。

从图 9和表 1中可以看出, 基于扩展卡尔曼滤波的定位系统在3种方法中具有最高的精度。相对于低通滤波和自适应残差滤波, 该方法可使定位精度提高。特别是当信噪比低于20时, 改善非常明显。所以在下面的仿真中, 以处理最小均方误差的规则作为最佳的估计标准, 并采用扩展卡尔曼滤波器, 以尽量减少声波中噪声的影响。

表1

不同滤波器在不同信噪比(SNR)的相位误差 %

3.2 改进四元基阵定位仿真

为了验证相对于传统基阵, 改进基阵测量所得基元间相位差的精度提升, 设计了如下的仿真实验。为了尽量实现测量船在多个角度的测量, 测量船以半径为r圆形的轨迹绕待测应答器运动, 实现了在0°~360°每隔角度Δγ测量应答器坐标。具体测量的示意图如图 10所示。

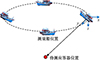图10

测量船的测量轨迹示意图

换能器发出的声波信号的频率为f₀, 长度为T_w。另外, 假设背景噪声为带宽f的高斯白噪声。假设在海洋中的声波速度不变, 为c, 采样率为f_s。声波信号通过扩展卡尔曼滤波降噪。与改进四元基阵对比的传统基阵基元之间的距离为d。仿真的相关参数如表 2所示。

设置信号的信噪比为15~30 dB, 对于每个信噪比, 分别采用改进四元基阵和传统基阵对应答器进行100次定位。为了实现2种基阵定位效果的对比, 通过控制变量法, 只考虑相位测量上的误差。测量船绕应答器1圈的测量位置和对应答器的定位结果如图 11所示。

图11

2种阵型定位结果

由2种基阵对应答器的定位结果可知, 改进四元基阵的定位误差低于传统基阵的定位误差, 且在不同的信噪比下, 定位精度均提升了近8倍。

加入改进八元基阵的定位结果, 在不同信噪比下的定位精度如表 3和图 12~15所示。可以得到改进四元基阵和改进八元基阵的定位精度大致相同。而通过不同信噪比的定位精度对比, 可以得出, 在超短基线定位系统基元阵型一样时, 提高声波信号的信噪比可以减小水下的定位误差, 如果在噪声不变的情况下, 可以通过提高声波信号的功率来实现。

信噪比为15 dB时的3种基阵定位误差

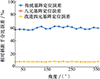信噪比为20 dB时的3种基阵定位误差

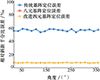信噪比为25 dB时的3种基阵定位误差

信噪比为30 dB时的3种基阵定位误差

仿真参数设计表

信噪比分别为15~30 dB时2种阵型定位误差 ‰

4 结论

针对超短基线系统在进行较远距离的定位时的相位模糊问题, 提出了一种改进新型四元基阵。该方法通过改变四元基阵中一个基元的位置, 有效地提高了基阵定位的精度, 减小了相位模糊问题。而针对接收到的声波信号由于噪声导致的相位差测量误差, 通过扩展卡尔曼滤波对信号进行了滤波, 有效地提升了相位差测量的精度。在仿真中, 利用最小二乘法解算出了应答器的准确位置, 作为对照, 将改进四元基阵与传统基阵和改进八元基阵的定位结果进行了对比, 得到的定位结果精度提升了将近一个数量级。

References

XU B, WANG X, ZHANG J, et al. Maximum current ropy delay Kalman filter for SINS/USBL integrated navigation[J]. ISA Transactions, 2021, 117: 274–287 [Google Scholar]
ZHAO Anbang, HE Wenxiang, DONG Haifang, et al. Deep sea ultra short baseline positioning algorithm with sound velocity distribution[J]. Journal of System Simulation, 2009, 21(15): 4763–4767 (in Chinese) [Google Scholar]
LIU H, WANG Z, SHAN R, et al. Research into the integrated navigation of a deep-sea towed vehicle with USBL/DVL and pressure gauge[J]. Applied Acoustics, 2020, 159: 107052 [Google Scholar]
LUO Caizhi, YANG Kun, XIN Mingzhen, et al. Robust Kalman filtering and its application in ultra short baseline underwater positioning[J]. Journal of Ocean Technology, 2020, 39(5): 46–52 (in Chinese) [Google Scholar]
DAJUN S, JIA G, JUCHENG Z, et al. Design of high accuracy ultra short baseline underwater acoustic position system[C]//2017 IEEE International Conference on Signal Processing, Communications and Computing, 2017: 1–4 [Google Scholar]
LEE H, KIM K, CHUNG T, et al. Deep learning-based ultra short baseline underwater positioning[C]//2023 International Conference on Artificial Intelligence in Information and Communication, 2023: 856–859 [Google Scholar]
WANG Yan, LI Qing, FU Jin, et al. Research on fusion classification and deblurring technology for ultra short baseline positioning systems[J]. Journal of Electronics and Information Technology, 2017, 39(6): 1348–1354 (in Chinese) [Google Scholar]
LI Haipeng, HAN Yunfeng, ZHENG Cui'e. Application of sound velocity correction technology in high-precision underwater positioning systems[J]. Journal of Navigation and Positioning, 2020, 8(3): 47–52. [Article] (in Chinese) [Google Scholar]
ZHANG Jucheng, ZHENG Cui'e, SUN Dajun. Adaptive layered method for acoustic line tracking and localization[J]. Journal of Harbin Engineering University, 2013, 34(12): 1497–1501 (in Chinese) [Google Scholar]
HUANG Jian, YAN Shenggang. Ultrashort baseline localization algorithm based on region partition adaptive particle swarm optimization[J]. Control and Decision, 2019, 34(9): 2023–2030. [Article] (in Chinese) [Google Scholar]
HUANG Minyan, YIN Feixing, LIU Bin. Research on the correction method of sound line bending error in ultra short baseline positioning system[C]//Proceedings of the 2016 National Acoustics Academic, 2016: 4 (in Chinese) [Google Scholar]
ZHANG Tao, WENG Chengcheng, LI Mohan, et al. A calibration algorithm for installation error of SINS/ultra short baseline integrated positioning system[J]. Journal of Inertial Technology of China, 2019, 27(3): 349–356. [Article] (in Chinese) [Google Scholar]
XIA M, ZHANG T, WANG J, et al. The fine calibration of the ultra-short baseline system with inaccurate measurement noise covariance matrix[J]. IEEE Trans on Instrumentation and Measurement, 2021, 71: 1–8 [Google Scholar]
LUO Yu, WANG Jingjing, SHI Jian. Overview of error calibration methods for ultra short baseline underwater acoustic positioning systems[J]. Industrial Innovation Research, 2022(10): 114–117 (in Chinese) [Google Scholar]
YU Baishi, WANG Zhanyong. Calibration method for ultra short baseline underwater acoustic positioning system based on least squares method[J]. Digital Ocean and Underwater Attack and Defense, 2020, 3(5): 408–415. [Article] (in Chinese) [Google Scholar]
JIN Bonan, XU Xiaosu, ZHANG Tao, et al. Ultra short baseline positioning technology and its application in ocean engineering[J]. Navigation, Positioning and Timing, 2018, 5(4): 8–20 (in Chinese) [Google Scholar]

All Tables

表1

不同滤波器在不同信噪比(SNR)的相位误差 %

仿真参数设计表

信噪比分别为15~30 dB时2种阵型定位误差 ‰

In the text

All Figures

	图1 超短基线水下定位系统的结构
In the text

	图2 超短基线定位原理示意图
In the text

	图3 超短基线相位差示意图
In the text

	图4 改进的八元基阵示意图
In the text

	图5 改进的四元基阵示意图
In the text

	图6 改进的四元基阵二维示意图
In the text

	图7 滤波前的声波信号
In the text

	图8 滤波后的声波信号
In the text

	图9 不同信噪比下不同方法相位误差
In the text

	图10 测量船的测量轨迹示意图
In the text

	图11 2种阵型定位结果
In the text

	图12 信噪比为15 dB时的3种基阵定位误差
In the text

	图13 信噪比为20 dB时的3种基阵定位误差
In the text

	图14 信噪比为25 dB时的3种基阵定位误差
In the text

	图15 信噪比为30 dB时的3种基阵定位误差
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] XU B, WANG X, ZHANG J, et al. Maximum current ropy delay Kalman filter for SINS/USBL integrated navigation[J]. ISA Transactions, 2021, 117: 274–287 [Google Scholar]

[2] ZHAO Anbang, HE Wenxiang, DONG Haifang, et al. Deep sea ultra short baseline positioning algorithm with sound velocity distribution[J]. Journal of System Simulation, 2009, 21(15): 4763–4767 (in Chinese) [Google Scholar]

[3] LIU H, WANG Z, SHAN R, et al. Research into the integrated navigation of a deep-sea towed vehicle with USBL/DVL and pressure gauge[J]. Applied Acoustics, 2020, 159: 107052 [Google Scholar]

[4] LUO Caizhi, YANG Kun, XIN Mingzhen, et al. Robust Kalman filtering and its application in ultra short baseline underwater positioning[J]. Journal of Ocean Technology, 2020, 39(5): 46–52 (in Chinese) [Google Scholar]

[5] DAJUN S, JIA G, JUCHENG Z, et al. Design of high accuracy ultra short baseline underwater acoustic position system[C]//2017 IEEE International Conference on Signal Processing, Communications and Computing, 2017: 1–4 [Google Scholar]

[6] LEE H, KIM K, CHUNG T, et al. Deep learning-based ultra short baseline underwater positioning[C]//2023 International Conference on Artificial Intelligence in Information and Communication, 2023: 856–859 [Google Scholar]

[7] WANG Yan, LI Qing, FU Jin, et al. Research on fusion classification and deblurring technology for ultra short baseline positioning systems[J]. Journal of Electronics and Information Technology, 2017, 39(6): 1348–1354 (in Chinese) [Google Scholar]

[8] LI Haipeng, HAN Yunfeng, ZHENG Cui'e. Application of sound velocity correction technology in high-precision underwater positioning systems[J]. Journal of Navigation and Positioning, 2020, 8(3): 47–52. [Article] (in Chinese) [Google Scholar]

[9] ZHANG Jucheng, ZHENG Cui'e, SUN Dajun. Adaptive layered method for acoustic line tracking and localization[J]. Journal of Harbin Engineering University, 2013, 34(12): 1497–1501 (in Chinese) [Google Scholar]

[10] HUANG Jian, YAN Shenggang. Ultrashort baseline localization algorithm based on region partition adaptive particle swarm optimization[J]. Control and Decision, 2019, 34(9): 2023–2030. [Article] (in Chinese) [Google Scholar]

[11] HUANG Minyan, YIN Feixing, LIU Bin. Research on the correction method of sound line bending error in ultra short baseline positioning system[C]//Proceedings of the 2016 National Acoustics Academic, 2016: 4 (in Chinese) [Google Scholar]

[12] ZHANG Tao, WENG Chengcheng, LI Mohan, et al. A calibration algorithm for installation error of SINS/ultra short baseline integrated positioning system[J]. Journal of Inertial Technology of China, 2019, 27(3): 349–356. [Article] (in Chinese) [Google Scholar]

[13] XIA M, ZHANG T, WANG J, et al. The fine calibration of the ultra-short baseline system with inaccurate measurement noise covariance matrix[J]. IEEE Trans on Instrumentation and Measurement, 2021, 71: 1–8 [Google Scholar]

[14] LUO Yu, WANG Jingjing, SHI Jian. Overview of error calibration methods for ultra short baseline underwater acoustic positioning systems[J]. Industrial Innovation Research, 2022(10): 114–117 (in Chinese) [Google Scholar]

[15] YU Baishi, WANG Zhanyong. Calibration method for ultra short baseline underwater acoustic positioning system based on least squares method[J]. Digital Ocean and Underwater Attack and Defense, 2020, 3(5): 408–415. [Article] (in Chinese) [Google Scholar]

[16] JIN Bonan, XU Xiaosu, ZHANG Tao, et al. Ultra short baseline positioning technology and its application in ocean engineering[J]. Navigation, Positioning and Timing, 2018, 5(4): 8–20 (in Chinese) [Google Scholar]