EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 582-591 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 582 - 591
DOI https://doi.org/10.1051/jnwpu/20254330582
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

未来战争逐渐趋向全球化作战方式, 高空长航程飞行器能在较短时间内跨越广阔的地理区域, 在减少人员直接参与的同时, 可以执行侦察、监测、干扰和精准打击等任务, 因此具有长航程飞行能力的飞行器将成为未来战场中的重要装备[1-2]。然而, 在处理长航程飞行器的航迹规划问题时, 地球表面近似为一个球面, 并非欧氏空间, 需要考虑地球曲率对航迹规划中航程计算的影响, 这提高了航迹规划的难度[3-4]。此外, 长航程飞行器需要在飞行过程中规避地球表面的障碍区, 如军事禁区、飞行限制区等, 需要在航迹规划算法中考虑障碍区约束以确保飞行安全性。

近年来, 针对复杂环境下的安全路径规划方法已有较多的研究成果, 主要有人工势场法、A*算法、Dijkstra方法以及随机快速搜索树(rapidly-exploring random tree, RRT)算法等[5-7]。其中Wang等[8]使用A*算法规划一条避开威胁的路径, 采用地形跟随/地形回避算法用于处理地形和威胁, 但是仅研究了圆形威胁区的情况, 针对复杂多边形威胁区没有给出相关结论。而Maini等[9]针对复杂的多边形障碍物, 采用改进的Dijkstra最短路径算法并结合Dubins轨迹得到满足动力学约束的飞行器航迹。在将合理避障作为研究重点的基础上, 杨萌等[10]针对传统人工势场法的局部震荡问题提出了解决方案, 对威胁区模型进行优化, 得到满足避障的最短航迹。但是该方法规划的航迹存在较大的拐点, 并不适合高速飞行器。传统的寻路算法或其改进方法只适用于二维或三维欧式空间, 而在球面空间中, 还需要针对曲率带来的影响进行深入研究。

为了处理球面空间中曲率对航迹规划方法的影响, 研究者们常采用投影方式先将球面坐标转换为平面坐标, 然后在平面坐标下进行航迹搜索。龚清萍等[11]提出了基于兰勃特等角投影的航迹投影方法, 应用等角条件将球面投影到圆锥面上, 然后沿母线展开得到兰勃特投影平面, 进而将航迹进行投影, 这种方法保持了地球上点之间的角度关系, 可视化效果好, 但会导致距离上的变形, 不太适用于大范围、纬度变化较大的航迹规划。冯朝晖等[12]针对曲面上的航迹规划问题, 提出了一种曲面趋平化算法(curved surfaced flattening algorithm, CSFA), 采用准均匀B样条曲面拟合算法对CSFA算法处理后的目标区域进行插值, 构建区域的自然环境地形模型, 但这种方法计算量过大。王兰等[13]采用降维映射的方法处理地球曲率对航迹规划的影响, 先用高斯投影将航迹规划空间投影到特定的高斯投影二维平面上, 之后根据高空长航时无人机的特性在降维后的二维高斯投影平面进行航迹规划。

综上所述, 目前针对长航程飞行器航迹的研究, 大多是通过投影方法将球面坐标转换到欧氏空间, 然后在二维或三维欧式空间中采用传统寻路方法进行路径搜索, 启发式函数仍然是通过欧式距离计算, 搜索得到的路径在球面上并不是最短路径[14]。因此, 为了在考虑曲率的同时消除规划场景范围对结果的影响, 需要在采用合理映射方法的基础上, 构建针对球面空间的寻路算法, 以构成高效、适用性强的长航程球面寻路搜索方法。

然而, 采用寻路方法获得的是非连续航迹点, 直接采用直线或者曲线连接并不具备速度的连续性, 无法用于航迹制导和跟踪。为解决这一问题, 近年来采用的方法主要有圆弧段串联法、平滑算子法、滤波法、B样条曲线法和Dubins曲线法等[15-16]。圆弧段串联法是针对存在尖锐夹角的相邻航迹段, 使用一系列相互连接的圆弧段, 将航迹进行曲线拟合[17-18]。李艳等[19]针对高速无人飞行器, 提出了结合遗传算法与Dubins轨迹的路径规划算法。郑昌文等[20]引入平滑算子来切除航迹中的尖锐夹角, 先随机选择某航迹点, 之后在与该航迹点相连的2个航迹段上, 分别插入1个新航迹点, 以此实现航迹的平滑。此外, 现有的路径搜索方法大多不考虑初末速度方向的约束, 获得的航迹结果对于整个飞行过程而言并不完整。

综上, 本文提出了DCS-Anya(Dubins-circle-spherical any-angle path-planning)的航迹规划方法, 可以在满足初末状态约束的基础上, 获得球面上的最短光滑连续航迹。

首先, 采用墨卡托投影建立栅格地图, 构建球面上多边形和圆形障碍区的描述方式; 其次, 使用地球大圆线劣弧长度作为启发式函数, 基于S-Anya算法设计了球面路径搜索算法, 并在此基础上, 采用几何曲线构建针对大圆航迹的航迹平滑方法, 形成CS-Anya方法; 然后, 采用Dubins方法构建临界切入/切出点的概念, 获取满足初末状态的局部最短航迹, 最后, 采用DCS-Anya方法获得满足初末状态和动力学约束的球面上光滑连续的最短大圆航迹。本文的主要贡献如下:

1) 基于S-Anya算法构建了球面上的DCS-Anya规划方法, 消除地球曲率给航迹规划带来的影响, 在满足初末状态约束的基础上, 获得球面上的光滑连续最短航迹。

2) 提出了一种针对大圆航线的航迹平滑方法, 构建了圆弧航迹和大圆航迹的平滑连接方式, 从而获得满足飞行要求的光滑连续航迹。

3) 提出采用Dubins方法满足初末状态约束, 并且根据大圆线的特点, 将初末状态的速度调整问题建模为在大圆线上寻找最优切入/切出点的寻优问题。

1 球面规划场景建模

本文采用球体墨卡托投影方法, 将地球表面投影为一个二维平面, 墨卡托投影是一种“等角正切圆柱投影”, 球体墨卡托投影(web Mercator projection)是墨卡托投影的变种[21], 该方法可在平面地图上保持方向和角度的正确, 广泛应用于航海与航迹图的绘制。在投影时为了简化计算, 将地球简化为半径为6 378.137 km的标准球体, 采用(1)式通过经纬度计算投影后坐标。

式中：R为地球近似半径；φ为纬度；λ为经度；λ0为参考点经度。球体墨卡托投影下, 投影坐标范围(单位: km)是

对应的地理坐标系下, 经度范围是[-180°, 180°]; 纬度范围是[-85.051 1°, 85.051 1°]。

地球上各类复杂障碍区可以分为不规则多边形和圆形障碍区, 由于球体墨卡托投影后的地图仍由经纬度坐标表示位置信息, 故原球面上障碍区的经纬度参数可以直接在投影后的地图上表示。以图 1所示的圆形障碍区为例, 通过圆心的经纬坐标及其半径, 可以计算圆形障碍区边界位置的经纬度, 根据所在栅格位置进行扩充, 即可得到投影地图下的障碍区。

thumbnail 图1

障碍区扩充示意图

由于在实际飞行过程中, 由于环境干扰和控制误差的存在, 飞行器通常无法严格按照规划的既定航迹飞行, 因此为保证整段航迹的安全性, 通过扩展障碍区范围的方式, 增加航迹的安全裕度[21]。如图 2所示, 以圆形和六边形为例, 在进行障碍区扩充之前设置安全裕度。

thumbnail 图2

安全区示意图

2 基于S-Anya算法的航迹规划方法

2.1 S-Anya算法

以经典A*寻路算法为例, 寻找后继节点时采取“八邻居制”, 通过欧氏距离计算启发函数的值。而Anya算法将每个节点定义成二元组(I, r), 其中r是根节点, I是从根节点r可达的最大区间, 从而获得任意角度的路径, 同时不受限于栅格地图的约束[22]。

大圆航线是地理航程最短的航线[23], 因此采用大圆线进行搜索过程得到的才是真正的最短航迹。S-Anya算法[24]是对Anya寻路算法的推广, 将寻路场景从二维扩展到三维球面, 采用大圆线进行前向探索, 并且计算任意两点间最短距离时采用大圆线距离。

S-Anya算法在寻路中的每个节点仍是二元组(I, r), 从起点出发, 沿经线逐层向终点方向搜索, 直至当前寻路节点(I, r)中的区间I包含终点坐标, 则停止寻路, 从终点返回航路点的经纬坐标, 通过大圆线连接获得完整航迹。S-Anya算法也是一种基于启发值的搜索类算法, 其启发值函数f的设计如下

式中，g=C(s, r1, r2, …, rcurrent)为起点到当前根节点的左右航路点之间的距离加和。h=C(rcurrent, t)根据当前节点的类型进行计算, 针对大圆曲线的特点, 讨论3种节点类型。

1) 平节点

根节点r与可达区间I(a, b)位于同一行, 如图 3所示, 此时算法启发值设置为

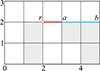thumbnail 图3

平节点示意图

2) 标准锥节点

根节点与可达区间不在同一行, 形成如图 4所示的“锥”形。

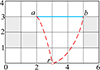thumbnail 图4

标准锥节点示意图

如图 5所示, 用大圆线连接r与点t, 该大圆线与区间I所在经线的交点记为p, 根据点p是否在区间I采用(5)式计算启发值。

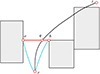thumbnail 图5

标准锥节点搜索方法

3) 伴随锥节点

如果当前节点在障碍区的边界上, 与标准锥节点类似, 如图 6所示, 用大圆线连接点r与点t, 该大圆线与区间I所在经线交点记为p, 根据点p是否在区间I采用(6)式计算启发值。

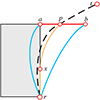thumbnail 图6

伴随锥节点搜索方法

式中，d-lat(r, a)表示纬线段ra的长度。

2.2 CS-Anya规划方法

通过S-Anya算法得到不连续的大圆航迹和离散航路点, 无法直接用于飞行器航迹制导与跟踪, 因此需要对搜索结果进行平滑处理, 获取光滑连续的飞行航迹。对于飞行器而言, 在既定轨迹的跟踪过程中, 曲率的连续变化会增大轨迹跟踪的难度[25], 因此很多研究者采用圆弧作为飞行器的轨迹, 即在满足动力学约束的基础上, 参考飞行器机动能力构建曲率为定值的圆弧航迹[26-28]。综上, 本文在S-Anya算法的基础上采用圆弧航迹进行航迹平滑方法设计, 形成可以获取动力学可行航迹的CS-Anya规划方法。

由于航迹段是大圆线, 无法直接计算切点获得圆弧航迹的起点, 并且大圆航线没有解析表达式, 难以构建函数关系进而求解切点, 因此, 采用直线连接圆弧航迹和大圆航迹。如图 7所示, 平滑后的航迹由三部分组成: 大圆航迹、直线段和圆弧航迹段。只需确定直线段和大圆航迹的交界点A1, A2、切点B1, B2以及圆弧航迹半径的大小, 就可以获得平滑后的航迹。

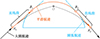thumbnail 图7

航迹平滑示意图

本文采用航迹平滑是为了获得可飞且能量损耗最小的航迹, 因此直线航迹和圆弧段航迹越短, 整体航迹的能量损耗就越小, 下面根据几何关系计算圆弧段和直线段的航迹长度, 首先定义A1, A2处切线的表达式为

式中, ki, bi(i=1, 2)为直线表达式的参数, 根据切线表达式和圆弧半径R, 计算圆弧段航迹对应圆心的位置(xc, yc)

通过求解(8)式, 获得圆心的位置(xc, yc)。其中, y=khx+bh为切线A1B1, A2B2角平分线的解析表达式, (xj, yj)为两直线的交点, 圆弧段的半径R根据飞行器的机动能力确定, 在获得了圆心位置后, 计算B1, B2的位置。

式中：i=1, 2分别对应B1, B2 2个切点；ki, bi为切线A1B1, A2B2的参数, 因此计算直线航迹的长度Ls为

圆弧段航迹长度Lc为

式中：d为2个切点的直线距离, 即圆的弦长; θ为弦长对应的圆心角, 过渡航迹的总长度Ltr为

综上可知, B1, B2的位置是在获取A1, A2后计算切线和圆弧切点获得的, 因此首先求解A1, A2的位置, Ai作为直线和大圆航线的过渡点, 必须在Bi之前。如图 8所示, 在圆弧航迹的半径确定的前提下, 如果Bi在Ai之后就没有合理的航迹解。

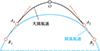thumbnail 图8

航迹平滑无解情况

下面构建无约束优化问题, 以最短过渡航迹为优化指标, 旨在寻找大圆航迹上A1, A2的最优位置, 通过构建代价函数描述Ai, Bi位置的约束条件。

式中：pA={xAi, yAi}(i=1, 2)代表A1, A2的位置信息；Pc代表大圆航迹上所有航迹点组成的向量空间, A1, A2要在该空间内找到最优值, JL是过渡段航程的代价函数, 通过(14)式计算。

式中, \begin{document}$L_{O A_1}^{\mathrm{c}}, L_{O A_2}^{\mathrm{c}}$\end{document}分别代表OA1, OA2段的大圆航线长度。Jp是航迹可行性的代价函数, w=[wL, wp]为权重系数。Jp通过计算航路点O和Ai, Bi的距离构建

式中，LA, LB分别为Ai, Bi和航路点O的距离, 当LB>LA时, 计算距离差值的平方作为代价函数, 当LB≤LA时, 满足可行性约束, 此时代价函数为0。通过求解(13)式中的优化问题, 获得最优的Ai, 进而实现航迹平滑。

2.3 满足初末状态约束的DCS-Anya方法

采用CS-Anya方法可以获得连续的最短航迹, 在此基础上, 本文采用Dubins方法对CS-Anya方法进行改进, 从而满足初末速度方向约束。

Pi和Pf分别表示一段Dubins航迹的起点和终点, 角度α和β分别表示起点和终点的方向角, 如图 9所示。Dubins规划方法可以在满足曲率半径约束的情况下, 找到从Pi到Pf的最短平滑航迹, 并满足初末速度方向约束[29]。

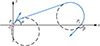thumbnail 图9

Dubins曲线起点和终点的方向角示意图

由于大圆航迹不具备解析表达式, 因此类比航迹平滑方法的设计思路, 采用直线作为圆弧轨迹和大圆航迹的过渡航迹。同时, 为保证全程航迹最短, 需要以最短的Dubins航迹实现速度方向的调整。在此, 建立临界切入点和临界切出点的解算方法, 分别对应起点附近调整速度方向后切入大圆航迹的切入点和终点附近由大圆航迹切出进行速度调节的点。

1) 临界切入点

临界切入点是起点附近调整速度方向后切入大圆航迹的切入点, 设计临界切入点是为了以最短的Dubins航迹实现速度方向的调整, 并将飞行器引导到由CS-Anya方法获取的球面最短航迹上。

如图 10所示, 采用Dubins方法可以在已知初末速度方向的基础上构建中间航迹, 而只有处于图 10中临界状态时才可以获得最短的Dubins航迹[29]。而当两圆相切时, 满足几何关系[30]

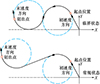thumbnail 图10

临界状态对比示意图

式中：R为转弯半径；d为Dubins航迹起终点间的欧氏距离。当满足上述条件后, Dubins航迹仅由两段圆弧组成, 形成最短航迹。当确定了初始速度方向后, 即确定了角度α。因此需要在已知α的基础上, 在大圆航线中寻找满足临界状态的点, 作为切入点。此外, 在进行速度调整后, Dubins航迹会与大圆航迹平滑相接, 构成整体的飞行航迹, 因此在考虑最短航迹时, 仅考虑Dubins航迹是不严谨的, 因此, 在采用Dubins方法后, 还需要考虑由起点开始第一段大圆航迹的剩余长度, 从而更加合理地获得全程的最短飞行航迹。因此构建以下优化问题

式中：U(xu, yu)为大圆航迹上的航迹点；yu=kuxu+bu代表在该航迹点处的切线, 不等式Ωu表示只有满足该条件, 才能保证Dubins方法有解并且仅采用圆弧航迹可以构成可行解。Lu为由起点开始第一段大圆航迹的剩余长度, λ1u和λ2u为权重系数。由于该问题的解空间对应大圆航迹上不等式Ωu范围内的离散点, 并且可行解的选取是从起点位置开始逐渐远离直到满足(18)式为止, 因此可以采用二分法[31], 在大圆航迹上进行搜索, 获得临界切入点。

2) 临界切出点

临界切出点的解算方式和临界切入点类似, 构建以下优化问题

式中：G(xg, yg)为大圆航迹上的航迹点；yg=kgxg+bg代表在该航迹点处的切线, 已知目标位置和速度末端方向后, 即已知β, 需要在大圆航迹中寻找合适的αg和dg。Lg为到达终点的最后一段大圆航迹的剩余长度, λ1g和λ2g为权重系数。与解算临界切入点相同, 采用二分法进行求解。

在获取了临界切入/切出点后, 采用圆弧-圆弧的形式构建满足速度方向约束的航迹。根据起点和临界切入点位置处飞行器的状态信息, 计算两侧机动圆的圆心坐标[30]。

2.4 DCS-Anya航迹规划算法总体流程

航迹规划算法流程如图 11所示。

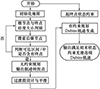thumbnail 图11

DCS-Anya航迹规划算法流程

2.5 DCS-Anya航迹规划算法伪代码

DCS-Anya算法伪代码如下所示：

1) 初始化地图(map, statei, statet)

2) map为含障碍物信息的地图矩阵, i表示初始点, t表示终点, root表示每一步探索根节点, state表示位置速度等状态信息, x表示经度, v表示经度搜索方向

3) while循环(xt∉I)

4) if(xroot>xt)

5) v<0, xnew=f(xroot, v), x=[x  xnew]

6) else if(xroot<xt)

7) v> 0, xnew=f(xroot, v), x=[x  xnew]

8) else

9) v=0, xnew=f(xroot, v), x=[x  xnew]

10) end while

11) 输出航迹转折点x

12) 无约束优化输出平滑后的过渡段圆弧轨迹

13) JL=Ltr-Lc=Ls+Lc-LcOA1-LcOA2为过渡段航程代价函数, Jp为航迹可行性代价函数

14) min(JL(pA)+Jp(pA))·w

15) 有约束规划生成临界切入点与切出点

16) 约束条件为初末状态, R为转弯半径, d为Dubins航迹起终点间的欧氏距离, 角度α和β分别为起点和终点的方向角

17) 输出满足初末状态约束光滑连续Dubins圆弧轨迹。

3 算法性能对比仿真验证

为进一步分析提出算法的规划效果, 将本文提出的DCS-Anya算法与A*搜索算法[32]对比, 验证DCS-Anya算法的性能和优点。在墨卡托投影后的二维平面上使用A*算法, 获得离散的航路点, 使用大圆航线连接所有离散点, 形成完整航迹。

1) 场景1

设定起点S经纬坐标为(44°, 47°), 目标点T经纬坐标为(12°, 22°), 设置2个多边形障碍区, 参数如表 1所示。为保证航迹的安全性, 对障碍区进行扩展处理, 边界向外延伸50 km, 采用半径150 km的圆弧曲线进行航迹平滑。

对比结果如图 12所示, CS-Anya算法和A*算法的寻路结果存在较大的差异, A*算法获得的航迹更加贴近障碍区, 在平滑圆弧航迹半径确定的情况下, 需要对障碍区设置更大的扩展范围, 以保证航迹的安全性。同时二者搜索到的最短路径不同, 分别从障碍区上下方绕过到达目标点。Anya算法获得的航迹更加平滑, 没有大的方向变化, 只和障碍区的点发生冲突, 不需要较大的扩展范围就可以保证航迹的安全性。

thumbnail 图12

场景1大圆航迹对比

对2种搜索方式同样采用大圆航线连接并进行航迹平滑后, CS-Anya获取航迹长度为4 280.794 km, A*算法航迹长度为4 484.396 km。相较于A*算法, Anya算法获得的航迹更短, 这是因为CS-Anya算法从“任意角度”以“大圆航线”向前探路, 并满足每次都找到最大可行区间, 因此得到的路径一定是球面上的最短路径。而A*算法则是受欧式距离启发值影响, 即便同样采用大圆航线连接A*算法寻到的航路点, 仍不是真正的最短航迹。

2) 场景2

本次场景考虑更多的障碍区, 设定起点S经纬坐标为(71°, 34.5°), 目标点T经纬坐标为(59°, 34°), 设置4个多边形障碍区, 参数如表 2所示。为保证航迹的安全性, 对障碍区进行扩展处理, 边界向外延伸20 km, 采用半径100 km的圆弧曲线进行航迹平滑。

对比结果如图 13所示, 2种算法都从障碍区中间穿过, 但是CS-Anya算法的离散航迹段更少, 航迹更加平滑, 只需要采用圆弧进行2次平滑过渡即可, 而A*算法需要4次平滑过渡。CS-Anya获取航迹长度为1 162.339 km, A*算法航迹长度为1 186.206 km。相较于A*算法, Anya算法获得的航迹更短, A*算法受欧式距离启发值影响, 并且算法特性更加贴近障碍区进行最短路径的搜索, 航迹的整体安全性也会受到影响。

thumbnail 图13

场景2大圆航迹对比

3) 场景3(初末状态约束场景)

通过上述场景的对比仿真验证, 可以看出所提出的CS-Anya算法可以获得球面的最短航迹, 并保证航迹安全性。为了进一步验证DCS-Anya方法在初末状态约束下的规划效果, 在场景中采用CS-Anya方法规划结果的基础上, 设置初末状态约束(初始方向-60°，末端方向60°，Dubins圆半径150 km), 进行仿真分析。

仿真结果如图 14所示, 在CS-Anya结果的基础上采用Dubins方法满足了初末状态约束, 并且采用Dubins方法构建圆弧轨迹和大圆航迹平滑连接, 满足了连续性要求。因此, 可以验证所建立的DCS-Anya方法可以实现满足初末状态约束的球面长航程规划, 得到满足安全要求的最短光滑连续航迹。

thumbnail 图14

场景3 DCS-Anya规划结果

表1

场景1障碍区设置

表2

场景2障碍区设置

4 结论

针对长航程飞行器的航迹规划问题, 本文提出了一种满足初末状态约束的DCS-Anya规划方法。首先, 通过墨卡托投影将规划球面投影成二维平面, 并给出了多种障碍区的描述方式, 通过扩展障碍区保证了平滑后航迹的安全性; 之后, 采用S-Anya算法进行寻路获取航路点, 采用大圆航线连接得到了真正的最短航迹; 接着, 基于几何曲线方法, 构建CS-Anya方法, 解决航迹段不连续的问题, 并在此基础上, 采用Dubins方法满足初末状态约束, 实现了圆弧航迹和大圆航迹的平滑连接, 从而获得满足飞行要求和初末状态约束的最优球面航迹。

与A*算法进行对比仿真实验, 结果表明, 本文提出的规划方法相比A*算法更加安全平滑, 并且得到的航迹更短。

本文构建的远距离航迹规划方法, 面临地图栅格精度和搜索步长的选取问题, 采用精度更高的栅格地图或采用更小的搜索步长, 可以提高搜索精度, 但是会增加算法的求解时间。针对本文所研究的远距离大范围规划方法, 合理降低地图精度和选择搜索步长不仅可以缩短规划时间, 还不影响规划结果的最优性。因此, 今后将进一步对所构建规划方法针对地图精度和搜索步长的自适应能力进行研究, 从而提升算法的灵活性和适应性。

References

  1. MA Dongli, ZHANG Liang, YANG Muqing, et al. Overview of key technologies for ultra long endurance solar unmanned aerial vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(3): 29–58. [Article] (in Chinese) [Google Scholar]
  2. WANG S. Flight strategy optimization for high-altitude long-endurance solar-powered aircraft based on Gauss pseudo-spectral method[J]. Chinese Journal of Aeronautics, 2019, 32(10): 2286–2298 [Google Scholar]
  3. TUZCU I, MARZOCCA P, CESTINO E, et al. Stability and control of a high-altitude, long-endurance UAV[J]. Journal of Guidance Control & Dynamics, 2007, 30(3): 713–721. [Article] [Google Scholar]
  4. DUAN H, FANG Y, ZHANG L. New thoughts on the development of a HALE UAV[J]. CAAI Trans on Intelligent Systems, 2012, 7(3): 195–199 [Google Scholar]
  5. ZOU Zhilong, ZHANG Liang. Simulation of missile battlefield penetration target trajectory planning[J]. Computer Simulation, 2019, 36(1): 97–101. [Article] (in Chinese) [Google Scholar]
  6. WEI Bowen, SHAO Changxu, WANG Maosen. Autonomous route planning of unmanned aerial vehicle group based on artificial potential field method[J]. Ordnance Industry Automation, 2018, 37(11): 84–88 (in Chinese) [Google Scholar]
  7. LI Zhaoying, OU Yiming, SHI Ruoling. Improved RRT path planning algorithm based on deep Q-network[J]. Air & Space Defense, 2021, 4(3): 17–23 (in Chinese) [Google Scholar]
  8. WANG H, LI Q, CHENG N. Real-time path planning for low altitude flight based on A* algorithm and TF/TA algorithm[C]//2012 IEEE International Conference on Automation Science and Engineering, 2012: 837–842 [Google Scholar]
  9. MAINI P, SUJIT P B. Path planning for a UAV with kinematic constraints in the presence of polygonal obstacles[C]//2016 International Conference on Unmanned Aircraft Systems, Arlington, VA, USA, 2016: 62–67 [Google Scholar]
  10. YANG Meng, WANG Yue. UAV avoidance trajectory planning based on improved artificial potential field method[J]. Navigation and Control, 2019, 18(1): 76–83 (in Chinese) [Google Scholar]
  11. GONG Qingping, XU Yu. Application of map projection in UAV route planning[J]. Avionics Technology, 2009, 40(2): 48–52 (in Chinese) [Google Scholar]
  12. FENG Zhaohui, HAN Liusheng, LI Qin. An improved method for three-dimensional trajectory planning of unmanned aerial vehicles[J]. Acta Geodaetica et Cartographica Sinica, 2021(3): 50–54 (in Chinese) [Google Scholar]
  13. WANG L, LI Y. A multi-objective optimization method based on dimensionality reduction mapping for path planning of a HALE UAV[C]//2019 Chinese Automation Congress, Hangzhou, China: 2019: 3189–319 [Google Scholar]
  14. IMADO F. A study on a missile guidance system against a randomly maneuvering air-to-surface missile[C]//Proceedings of the 2004 IEEE International Conference on Control Applications, 2004: 430–435 [Google Scholar]
  15. SINGH R. Trajectory planning and optimization for UAV communication: a review[J]. Journal of Discrete Mathematical Sciences and Cryptography, 2020, 23(2): 475–483 [Google Scholar]
  16. ZHANG H, LIN W, CHEN A. Path planning for the mobile robot: a review[J]. Symmetry, 2018, 10(10): 450–466 [CrossRef] [Google Scholar]
  17. WEI Qiao, ZHAO Yingjun, YU Qun, et al. Improved particle swarm optimization algorithm for cruise missile path planning[J]. Electronics Optics & Control, 2008, 15(3): 49–52. [Article] (in Chinese) [Google Scholar]
  18. MA Yunhong, ZHOU Deyun. Unmanned aerial vehicle path planning algorithm and simulation[J]. Fire Control & Command Control, 2007, 32(6): 33–36 (in Chinese) [Google Scholar]
  19. LI Yan, GUO Jifeng, LUO Rubin. Path planning of high-speed unmanned systems in multi obstacle environments based on genetic algorithm and Dubins theory[J]. Unmanned Systems Technology, 2021, 4(6): 37–45. [Article] (in Chinese) [Google Scholar]
  20. ZHENG Changwen, LI Lei, XU Fanjiang, et al. Multi route planning of unmanned aerial vehicles based on evolutionary computation[J]. Journal of Astronautics, 2005, 26(2): 223–227 (in Chinese) [Google Scholar]
  21. SATAI H A L, ZAHRA M M A, RASOOL Z I, et al. Bézier curves-based optimal trajectory design for multirotor UAVs with any-angle pathfinding algorithms[J]. Sensors, 2021, 21(7): 2460–2481 [Google Scholar]
  22. DANIEL H, ALBAN G, DINDAR Ö, et al. Optimal any-angle pathfinding in practice[J]. Journal of Articial Intelligence Research, 2016, 56(89): 89–118 [Google Scholar]
  23. WEINSTOCK R. Calculus of variations: with applications to physics and engineering[M]. New York: Courier Corporation, 1974 [Google Scholar]
  24. VOLODYMYR R, RUPERT S. Optimal any-angle path finding on a sphere[J]. Journal of Articial Intelligence Research, 2020, 1(15): 475–505 [Google Scholar]
  25. STEPHAN J, PFEIFLE O, NOTTER S, et al. Precise tracking of extended three-dimensional dubins paths for fixed-wing aircraft[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(12): 2399–2405. [Article] [Google Scholar]
  26. SONG X, HU S. 2D path planning with dubins-path-based A algorithm for a fixed-wing UAV[C]//2017 3rd IEEE International Conference on Control Science and Systems Engineering, Beijing, China, 2017: 69–73 [Google Scholar]
  27. SHANMUGAVEL M, TSOURDOS A, WHITE B, et al. Co-operative path planning of multiple UAVs using Dubins paths with clothoid arcs[J]. Control Engineering Practice, 2010, 18(9): 1084–1092. [Article] [Google Scholar]
  28. OWEN M, BEARD R W, MCLAIN T W. Implementing Dubins aircraft paths on fixed-wing UAVs[M]. VACHTSEVANOS G J, VALAVANIS K P. Handbook of unmanned aerial vehicles. Dordrecht: Springer, 2014: 1677–1701 [Google Scholar]
  29. DUBINS L E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents[J]. American Journal of Mathematics, 1957, 79(3): 497–516 [CrossRef] [Google Scholar]
  30. SHKEL A M, LUMELSKY V. Classification of the Dubins set[J]. Robotics and Autonomous Systems, 2001, 34(4): 179–202. [Article] [CrossRef] [Google Scholar]
  31. EIGER A, SIKORSKI K, STENGER F. A bisection method for systems of nonlinear equations[J]. ACM Trans on Mathematical Software, 1984, 10(4): 367–377 [Google Scholar]
  32. LIU X, GONG D. A comparative study of A* algorithms for search and rescue in perfect maze[C]//2011 International Conference on Electric Information and Control Engineering, 2011: 24–27 [Google Scholar]

All Tables

表1

场景1障碍区设置

In the text
表2

场景2障碍区设置

In the text

All Figures

thumbnail 图1

障碍区扩充示意图
In the text
thumbnail 图2

安全区示意图
In the text
thumbnail 图3

平节点示意图
In the text
thumbnail 图4

标准锥节点示意图
In the text
thumbnail 图5

标准锥节点搜索方法
In the text
thumbnail 图6

伴随锥节点搜索方法
In the text
thumbnail 图7

航迹平滑示意图
In the text
thumbnail 图8

航迹平滑无解情况
In the text
thumbnail 图9

Dubins曲线起点和终点的方向角示意图
In the text
thumbnail 图10

临界状态对比示意图
In the text
thumbnail 图11

DCS-Anya航迹规划算法流程
In the text
thumbnail 图12

场景1大圆航迹对比
In the text
thumbnail 图13

场景2大圆航迹对比
In the text
thumbnail 图14

场景3 DCS-Anya规划结果
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.