| Issue |
JNWPU
Volume 37, Number 1, February 2019
|
|
|---|---|---|
| Page(s) | 167 - 176 | |
| DOI | https://doi.org/10.1051/jnwpu/20193710167 | |
| Published online | 03 April 2019 | |
Numerical Simulation on Aerodynamics of Multi-Element Airfoil with Drooped Spoiler in Ground Effect
带扰流板下偏的多段翼型地面效应数值模拟
1
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
2
Department of Floating Platform, No. 38 Research Institute of CETC, Hefei 230088, China
3
Unmanned System Research Institute, Northwestern Polytechnical University, Xi’an 710072, China
4
AVIC Aerodynamics Research Institute, Sheng yang 110034, China
Received:
1
February
2018
By using the finite volume method and k-ω SST turbulence model to solve the Reynolds Average Navier-Stokes equation and using the slipping wall to simulate the relative movement of the ground, the ground effect on the aerodynamic characteristic of multi-element airfoil with drooped spoiler is investigated numerically, and the reason why the lift coefficient decreased in ground effect is analyzed. The results indicate that, with the reduction in ride height, the lift and the drag decrease and the lift-drag ratio increases for the multi-element airfoil; the amplitude of the reduction in the lift coefficient increases with the reduction in ride height and the increase in the angle of attack, the maximum of lift coefficient can be reduced by about 22%; with the effect of ground, the losses of suction at upper surface make the lift decrease, the increases of pressure at lower surface make the lift increase, the variation of the lift coefficient for the main wing caused by the former is more than three times that of the latter. Analyzing the reason why the lift coefficient decreases showed that:on the one hand, ground effect on the lift coefficient for clean airfoil is changed with the range of angle of attack. For the low-to-moderate angle of attack, the lift coefficient increases; for the high angle of attack, the lift coefficient decreases. But multi-element airfoil works in the takeoff and landing stage for the high angle of attack, which causes the reduction of the lift coefficient in ground effect. On the other hand, the increase of the lift coefficient caused by the deflection of spoiler decreases with the reduction in ride height and the maximum reduction can be about 50%, which illustrates that ground effect makes interaction of the front and back section for the multi-element airfoil weak, resulting in further decreasing the coefficient for the multi-element airfoil.
摘要
采用有限体积法和k-ω SST湍流模型求解雷诺平均N-S方程,使用运动壁面边界条件模拟地面的相对运动,研究了地面效应对带扰流板下偏的多段翼型气动特性的影响,并分析了地效影响下升力系数减小的原因。结果表明:随着离地高度的减小,多段翼型的升力和阻力减小,升阻比有所增大;升力系数的减小幅值随着离地高度的减小和迎角的增大逐渐增大,最大可以减小22%左右;地效影响下,主翼上表面吸力减小导致的升力系数减小幅值是下表面压力增大导致的升力系数增大幅值的3倍以上。升力系数减小原因分析表明:①地面效应对干净翼型升力系数的影响与迎角范围有关,在中小迎角下升力系数增大,在大迎角下升力系数减小,而多段翼型往往工作在大迎角下的起降阶段,故其升力系数在地效作用下减小;②扰流板下偏前后的升力系数增量随着离地高度的减小而减小,最大减小量可以达到50%左右,说明地面效应使得多段翼型前后部件之间的增升作用减弱,从而导致多段翼型的升力系数进一步减小。
Key words: multi-element airfoil / deflection of spoiler / ground effect / numerical simulation / CFD / high-lift devices / flow mechanism / aerodynamic characteristic / angle of attack / drag coefficient / flow fields / lift drag ratio / Mach number / turbulence models
关键字 : 扰流板下偏 / 多段翼型 / 地面效应 / 数值模拟 / 气动性能
© 2019 Journal of Northwestern Polytechnical University
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
增升装置气动性能的好坏对民机起降阶段整体性能的优劣起着关键性的作用。对于一架典型的双发喷气式民用运输机来说, 起飞时, 全机升阻比1%的增量可以转化为1 270 kg的商载; 着陆时, 在进场速度不变的条件下, 最大升力系数增加1%将多载22名乘客或近2 000 kg的货物[1-2]。新一代宽体客机, 如波音787及空客350客机均采用简单襟翼及定轴旋转机构, 以方便实现巡航阶段改变机翼的后缘弯度。然而, 简单襟翼的效率普遍会低于传统的富勒襟翼。因此为了保证起飞着陆阶段较好的气动性能, 需要下偏扰流板, 以保证良好的缝道参数, 提高增升装置效率[3-4]。
当飞机接近地面飞行时, 如起飞、着陆阶段, 迫使被其扰动的气流方向向平行于地面的方向改变, 作用在飞机上的气动力也发生改变, 这种现象被称作地面效应[5]。文献[6-7]指出地面效应对干净构型和增升构型的影响规律不同。例如普通干净构型的地效飞行器在近地飞行时, 升力增加, 可以获得较大的升阻比, 从而提高巡航效率。而文献[8]的研究表明地面效应使得多段翼型的升力系数减小, 这将直接影响飞机的起降性能。因此, 研究地面效应对带扰流板下偏的多段翼型气动性能的影响, 对于我国发展远程宽体客机具有重要的实际意义。
目前, 国内外学者对单段翼型地面效应已经进行了大量的研究, 而对多段翼型的研究工作较少。Hsiun等[9]通过数值模拟研究了弯度和厚度对二维翼型地面效应的影响, 发现下翼面与地面之间的气流通道决定了翼型的气动特性; Ahmed等[7]对迎角0°~10°范围内NACA4412翼型的地面效应进行了实验研究, 实验结果表明随着离地高度逐渐减小, 阻力逐渐增大, 但升力系数变化趋势取决于随迎角变化的翼型下表面与地面之间的气流通道形状; 屈秋林等[10]对NACA4412翼型在大范围迎角下的地面效应进行了数值模拟, 结果表明升力系数变化趋势取决于有效迎角减小导致的升力减小幅值和阻塞效应导致的升力系数增大幅值之间的相对大小, 中小迎角下, 前者小于后者, 升力系数增大; 大迎角下, 前者大于后者, 升力系数减小; 对于两段翼型, 屈秋林等[11]对带襟翼的NACA4412翼型进行了数值模拟, 结果表明迎角对两段翼型地面效应的影响与单段翼型类似。多段翼型地面效应的研究, 主要集中在对30p30n翼型的气动特性的计算[8, 12-13]。这些研究涉及的都只是升阻力特性和流场特性的简单分析, 都得到了与单段翼型升力特性不同的变化规律, 定性地说明了升力系数变化的原因, 但都没有对其进行详细定量地解释。
本文采用RANS方程结合k-ω SST湍流模型的CFD方法, 针对带扰流板下偏的多段翼型的地面效应进行数值模拟, 通过对升力系数、阻力系数、升阻比系数、压力分布和空间速度型的分析, 得到地面效应对多段翼型气动特性的影响规律, 并从迎角范围和增升作用两个角度细致地阐述了地效影响下升力系数减小的原因。
1 计算方法
1.1 数值方法
近些年来, 基于雷诺平均Navier-Stokes(RANS)方程的流场求解方法已在工程设计中的得到广泛应用[14], 其控制方程为:
连续方程
动量方程
能量方程
式中, ρ为密度, t为时间, ui为速度分量, xi为位置矢量, p为压强, e*为广义内能, τij为黏性应力张量分量, qj为热流分量。
本文基于ANSYS CFX软件并采用有限体积法进行RANS方程的离散, 空间离散格式为二阶迎风Roe格式, 该格式不仅能在求解精度与求解效率之间达到较好的平衡, 并在实际中得到了广泛运用, 而且其计算精度能满足对分离流等复杂流动现象的捕捉; 时间推进方式采用LU-SGS隐式时间推进算法。
1.2 湍流模型
为了封闭RANS方程, 本文采用Menter提出的k-ω SST湍流模型[15], 其具体方程式如下
式中, k和w分别为湍动能和湍流比耗散率, μ和μt分别为层流和湍流系数。生成源项P和函数F1的形式以及系数β*, γ, σk, σw和σw2的值可参考文献[15]。
k-ω SST湍流模型在边界层内部采用Wilcox k-ω模型, 在边界层边缘和自由剪切层采用高雷诺数Jones-Launder k-ε模型, 其间通过一个混合函数F1进行过渡, 属于积分到壁面的两方程涡黏性模型。该湍流模型充分利用了k-ω模型对逆压梯度流动具有较高的模拟精度以及k-ε模型对湍流初始参数不敏感的优点, 同时避免了两者的缺点。故该模型既适合计算附面层流动, 也适合计算分离流动离开物面之后在空间的发展。国内外的大量实践表明k-ω SST湍流模型能够比较准确地模拟航空航天领域的分离流、漩涡流等复杂流动现象[16]。
1.3 计算模型与边界条件
本文采用的多段翼型为某民用运输飞机着陆构型的kink位置剖面翼型, 由缝翼、主翼、扰流板和襟翼四部分组成, 其中缝翼偏转25°, 襟翼偏转38°, 扰流片下偏角度为10°, 襟翼的缝道宽度为2.08%, 搭接量为0.64%。计算状态为:Ma=0.2, 参考高度为海平面, 参考弦长c=6.523 3 m。计算构型如图 1所示, 坐标原点取在干净翼型1/4弦长处, 来流方向平行于地面, 迎角α通过偏转翼型得到, V∞为远场来流速度, h为多段翼型离地高度。
计算网格如图 2所示, 计算外区域选取为50倍弦长, 网格单元数为73 216。研究表明, 精心设计的多块结构网格较之非结构网格在模拟增升装置方面能够获得更为优秀的流场结果和计算精度[17]。为了尽量准确地捕捉流场细节, 本文提到的所有构型均采用多块结构网格, 并对流场参数梯度变化比较剧烈的区域(比如前缘、缝道、各部件之间的缝隙等)进行大量的加密。多段翼型表面满足无滑移边界条件, 运动地面满足如下边界条件(u, v)=(V∞, 0), ∂p/∂n=0, n为地面法向方向。
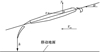 |
图1 多段翼型地面效应示意图 |
 |
图2 多段翼型地面效应计算网格 |
2 计算方法的可靠性验证
2.1 Tyrell-026反转翼型
为了验证本文计算地面效应采用的计算方法和边界条件的可行性, 采用有实验数据的反转赛车翼型Tyrrell-026进行流场数值模拟[18], 计算构型如图 3a)所示, 网格单元数为19 280。计算条件为风洞实验工况:V∞=30 m/s, Re=4.6×106, α=3.6°, h/c=0.224和h/c=0.671, 参考弦长c=0.223 4 m。计算得到的2个高度下的压力分布与实验结果的对比如图 3b)和图 3c)所示, 可以看出, 计算结果与实验结果吻合较好。该算例表明本文采用的计算方法可以适用于地面效应的数值模拟。
 |
图3 Tyrell-026构型及计算结果 |
2.2 二维L1T2构型算例
采用二维增升装置标模L1T2进行计算方法可信度的验证[19]。计算网格如图 4a)所示, 网格单元数为84 000。计算条件为风洞试验工况:Ma=0.197, Re=3.52×106。计算所得的升力系数曲线和阻力系数曲线与风洞实验结果对比分别如图 4b)和图 4c)所示, 从图中可以看出:①在失速迎角附近, 升力系数和阻力系数与实验结果差距明显, 这主要是因为k-ω SST湍流模型不能十分精确模拟分离区域造成的[14]; ②阻力系数在0°~8°攻角范围与实验值差距较为明显, 文献[20]的研究指出L1T2多段翼型阻力系数的精确预测是困难的, 因为网格的疏密和分布、转捩位置的预测精度、远场区域的大小和湍流模型的种类等都会对其造成不同程度的影响。需要说明的是, 本文重点关注线性段升力系数的变化, 所以此计算方法可以满足数值模拟的需求。
 |
图4 L1T2网格及计算结果 |
3 地面效应对气动特性的影响
采用上述数值方法对图 1所示的多段翼型进行地面效应的数值模拟, 计算迎角α=8°, 12°, 16°, 离地高度h/c=0.2, 0.4, 1.0, 2.0, 4.0, 10.0, 20.0, 50.0, 计算得到的不同迎角下气动力系数随离地高度的变化如图 5所示。从图中可以看出, 随着离地高度的减小, 3个不同迎角下的升力系数和阻力系数明显减小, 升阻比系数有所增大, 且越靠近地面(h/c < 1.0时), 升力系数损失速度越快, 且升力系数的减小幅值最大可以达到22%左右。
图 6为不同迎角下翼型表面压力系数分布随离地高度的变化。由图可知, 3个迎角下, 随着离地高度的减小, 前缘缝翼、主翼、扰流板和后缘襟翼上表面的吸力都明显减小, 而下表面的压力只是略有增加, 同时随着离地高度的降低, 下表面的压力分布趋于平缓。由Ahmed[7]和屈秋林[10]关于单段翼型地面效应的研究可知, 随着单段翼型距离地面高度的减小, 地面效应迫使绕过翼型的气流方向朝着平行与地面的方向改变, 从而使来流有效迎角减小, 上表面的吸力减小, 升力系数减小; 而翼型下表面由于阻塞作用, 压力增加, 升力系数增加; 上表面吸力减小幅值和下表面压力增加幅值的相对大小决定了升力系数增加还是减小。从图 6可以看出, 多段翼型下表面由于阻塞作用, 压力也是增加的。图 7给出了α=8°时主翼驻点处流线速度矢量角度β(速度矢量与x轴的夹角)随离地高度的变化, 由图可知, 随着离地高度的减小, 驻点处流线速度矢量角减小, 从而导致有效迎角减小, 反映在图 6b)中主翼上表面吸力的减小。
为了更加详细地说明主翼上表面吸力的减小的原因, 图 8给出了α=8°时不同离地高度下主翼上表面2个监测位置处的速度型对比。图 8a)为2个监测位置的示意图, 其中x/c=0.1位置在主翼头部附近, x/c=0.5处在主翼中部附近。图 8b)和图 8c)为2个位置处不同离地高度下的速度型对比, 图中横坐标为速度大小与远场来流速度大小的比值, 纵坐标为离开物面的法向距离与弦长的比值。从图中可以看出, 随着离地距离的减小, 在2个监测位置处距离物面相同距离处的速度逐渐减小, 即主翼上方压力增大, 吸力减小; 在x/c=0.5位置处, 当V/V∞=1时, 随着离地距离的减小, 距离物面的法向距离逐渐增大, 即附面层厚度逐渐增加, 从而在相同的逆压梯度下更容易产生分离。前缘缝翼、扰流板和后缘襟翼的变化规律与主翼相同。
 |
图5 地面效应下不同迎角的气动力系数 |
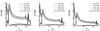 |
图6 翼型表面压力系数随离地高度的变化 |
 |
图7 α=8°时主翼驻点处流线速度矢量角随离地高度的变化 |
 |
图8 α=8°时不同离地高度下速度型测量位置和速度型对比 |
4 地效影响下升力系数减小原因分析
上一节计算结果分析表明, 随着距离地面高度的减小, 多段翼型的上表面吸力减小, 下表面压力增大, 而上表面吸力减小的幅值大于下表面压力增大的幅值, 从而使得升力系数减小。不同于单段翼型, 多段翼型存在前后各个部件的相互作用, 如襟翼后缘产生的环量对主翼的上洗作用使得主翼升力增加, 如果襟翼升力减小, 主翼升力损失较大, 即增升作用减弱。因此, 本节将从迎角范围和增升作用2个角度来详细地说明地效影响下多段翼型升力系数减小的原因。
4.1 迎角范围的影响
不同于地效飞行器接近地面巡航飞行时, 飞行迎角很小, 升力系数随离地高度的减小逐渐增大; 现代民用客机着陆时通常打开增升装置, 在较大飞行迎角下进行着陆, 升力系数随离地高度的减小逐渐减小。已有文献研究表明, 地面效应对升力系数的影响随迎角范围的变化截然不同。因此有必要研究地面效应在不同迎角范围内对单段翼型升力系数的影响规律, 并以此分析由多个单段翼型组成的多段翼型在较大迎角下升力系数随离地高度变化的原因。本文选取的单段翼型为图 1着陆构型对应的巡航构型, 如图 9所示, 计算状态与着陆构型保持一致, 计算迎角α=0°~12°, 间隔2°, 离地高度h/c=0.1,0.2,0.4,1.0,50.0。
为了更加直观地说明地面效应对上下表面升力系数的影响, 本文对升力系数和相关符号做了如下定义:
一个翼型的总升力系数定义如下:
式中, p为当地静压, p∞自由来流静压, Sup为翼型上表面的面积, 为翼型下表面的面积, n为翼型表面外法向单位矢量, τ为翼型表面的剪切应力, j为y方向的单位矢量。
一个翼型上表面的总升力系数定义如下
一个翼型下表面的总升力系数定义如下
总升力系数与上下表面升力系数关系
随着离地高度的变化, 总的升力系数和上下表面的升力系数相对h/c=50.0的差量定义如下
图 10给出了巡航翼型不同迎角下总的升力系数和上下翼面的升力系数随离地高度的变化趋势。图 11给出了巡航翼型不同迎角下总的升力系数差量和上下翼面的升力系数差量随离地高度的变化。
结合2幅图, 可以得出如下结论:
1) 在没有地面效应(h/c=50.0)时, 总的升力系数随迎角增大呈线性增长, 出现地面效应后(h/c≤1.0), 总的升力系数随迎角增大呈非线性的凸增长, 且离地距离越小, 凸增长的趋势越明显。因此, 出现地效的升力曲线与没有地效的升力曲线产生左右2个交点, 如图 10a)所示。
2) 在2个交点范围内的迎角下, 地面效应使总的升力系数增大; 在2个交点范围之外的迎角下, 地面效应使得总的升力系数减小。从图 11a)可以看出, 2个交点的迎角范围随离地距离减小而增大, 且都在迎角α=4°附近取得总的升力系数增量最大值, 但在大迎角α=12°时, 地面效应都使总的升力系数减小。
3) 从图 11a)可以看出, 出现地面效应的临界离地高度随迎角变化而变化。在迎角α=0°和2°时, 临界离地高度大约为1倍弦长; 在中大迎角α=4°~12°时, 临界离地高度明显大于1倍弦长。
4) 在所有的计算迎角下, 地面效应都使上表面升力系数减小, 且随着离地高度的减小和迎角的增大, 上表面升力系数减小的幅值一直单调增大; 在α=0°, h/c=0.1, 0.2时, 地面效应使得下表面升力系数减小, 在其余迎角和离地高度下, 地面效应都使下表面升力系数增大, 且在α=2°~8°的范围内, 下表面升力系数增大的幅值随迎角增大而增大, 在α=8°~12°的范围内, 下表面升力系数增大的幅值随迎角增大而减小, 。上表面升力系数减小幅值和下表面升力系数增大幅值的相对大小决定了总的升力系数增大还是减小, 因此, 在较大迎角(α≥10°)下, 上表面升力系数减小幅值随迎角一直增大, 而下表面升力系数增大幅值随迎角却逐渐减小, 从而使得总的升力系数减小。
图 12给出了多段翼型主翼不同迎角下总的升力系数差量和上下翼面的升力系数差量随离地高度的变化。从图中可以看出, 首先, 在计算迎角α=8°~16°范围内, 主翼总的升力系数随着迎角的增大和离地距离的减小一直减小, 且减小幅值越来越大, 例如h/c=1.0到h/c=0.4, α=8°, 主翼升力系数损失了5.66%, α=12°, 主翼升力系数损失增加到6.92%, α=16°, 主翼升力系数损失达到7.90%。其次, 上表面升力系数减小幅值随着迎角增大和离地距离减小一直增大, 而下表面升力系数幅值随着迎角增大和离地距离减小逐渐减小, 而在相同迎角和离地距离下, 主翼上表面升力系数减小幅值是下表面升力系数增大幅值的3倍以上, 例如α=12°, h/c=0.4时, |ΔCL, up|=0.685 3, |ΔCL, low|=0.109 8,前者是后者的6.24倍, 从而使得主翼总的升力系数大幅度减小。最后, 由于多段翼型绝大多数时候用在大迎角起飞着陆阶段, 而此时地面效应使得多段翼型总的升力系数明显减小, 因此有必要考虑多段翼型的工作状态, 以此分析地面效应对增升装置气动特性的影响。
 |
图9 巡航构型示意图 |
 |
图10 巡航翼型不同迎角下总的升力系数和上下翼面的升力系数随离地高度的变化 |
 |
图11 巡航翼型不同迎角下总的升力系数差量和上下翼面的升力系数差量随离地高度的变化 |
 |
图12 多段翼型主翼不同迎角下总的升力系数差量和上下翼面的升力系数差量随离地高度的变化 |
4.2 增升作用的影响
20世纪70年代, Smith[21]提出了在多段翼型绕流中缝道的5个主要有利影响。上游部件单元的环量会对其后方的单元诱导产生一个下洗影响, 比如缝翼产生的下洗会诱导一个与主翼来流方向相反的速度, 从而降低主翼的吸力峰值; 下游部件单元产生的环量会对前方单元诱导产生一个上洗影响, 比如襟翼产生的环量会对主翼后缘诱导产生一个上洗流动, 从而提高主翼的升力。而多段翼型在地面效应影响下, 各部件的升力都有所减少, 从而使得增升作用产生的升力增量减少, 例如地面效应使得襟翼升力的减小, 襟翼产生的环量减小, 对主翼的上洗作用减弱, 结果使得主翼的升力系数进一步减小。
从4.1节的巡航翼型和多段翼型主翼总的升力系数差量对比可以看出, 在相同迎角和离地距离下, 主翼升力系数减小幅值远远大于巡航翼型升力系数减小幅值, 例如, α=12°, h/c=0.4时, 巡航翼型升力系数减小0.124, 多段翼型主翼升力系数减小0.576, 后者远远大于前者, 故增升作用减弱导致的升力系数减小对于地面效应下的多段翼型总升力系数减小量来说是不容忽视的。因此, 本文选取图 13a)所示的扰流板不偏构型和图 1所示的扰流板下偏10°构型, 进行地面效应的数值模拟, 需要说明的是, 为了保持扰流板下偏前后缝道参数保持不变, 襟翼的位置有所变化, 但计算时保证2个构型的离地高度h是相同的。通过对比2个构型升力系数差量随离地高度的变化, 来定量地分析地面效应对增升作用的影响。
图 13b)和图 13c)分别给出了α=8°时扰流板不偏和下偏的多段翼型升力系数及其差量随离地高度的变化, 从图中可以看出, 首先, 在没有地效时(h/c=50.0), 扰流板下偏10°后, 相比于不偏构型, 升力系数增大了0.438, 即增大了20%左右, 这也验证了扰流板下偏作为一种流动控制技术, 可以达到增升的目的; 其次, 扰流板不偏和下偏2个构型的升力系数都随离地高度的减小而减小; 最后, 随离地高度的减小, 2个构型的升力系数差量明显减小, 即地面效应使得扰流板下偏的增升作用减弱, 例如, h/c=50.0到h/c=0.4, 升力系数差量从0.438减小到0.247, 减小了约43.6%。
 |
图13 α=8°时扰流板不偏和下偏的多段翼型升力系数及其差量随离地高度的变化 |
5 结论
本文通过数值模拟研究了地面效应对带扰流板下偏的多段翼型气动特性的影响, 并从迎角范围和增升作用2个角度细致地分析了升力系数减小的原因, 根据上述讨论, 可以得到如下结论:
1) 随着离地高度的减小, 多段翼型的升力系数和阻力系数明显减小, 升阻比系数有所增大。且升力系数的减小幅值随着离地高度的减小和迎角的增大逐渐增大, 最大可以减小22%左右。
2) 随着离地高度的降低, 地面效应使得来流有效迎角减小, 上表面吸力明显减小, 附面层变厚; 阻塞效应使得下表面压力略有增大。在相同迎角和离地距离下, 主翼上表面升力系数减小幅值是下表面升力系数增大幅值的3倍以上, 结果使得总升力系数明显减小。
3) 在中小迎角下, 巡航单段翼型随着离地高度的减小升力系数增大; 在大迎角下, 巡航单段翼型随着离地高度的减小而升力系数减小。由于多段翼型常工作在飞机起飞着陆的大迎角阶段, 因而地面效应使得多段翼型的升力系数减小。
4) 扰流板下偏前后的升力系数增量随着离地高度的减小而明显减小, 例如, h/c=50.0到h/c=0.4, 升力系数增量减小了约43.6%, 说明多段翼型前后部件之间的增升作用随着离地高度的减小逐渐减弱, 这也是多段翼型升力系数减小量远远大于相同情况下巡航翼型升力系数减小量的主要原因。
References
- Nakayama H, Kim H J, Matsushima K, et al. Aerodynamic Optimization of Multi-Element Airfoil[C]//AIAA Aerospace Sciences Meeting and Exhibit, 2006 [Google Scholar]
- Meredith P T. Viscous Phenomena Affecting High-Lift Systems and Suggestions for Future CFD Development[C]//Agard Conference Proceedings 515 High-Lift System Aerodynamics, 1993, 19: 1-8 [Google Scholar]
- Scholz P, Mahmood S, Casper M, et al. Design of Active Flow Control at a Drooped Spoiler Configuration[C]//AIAA Applied Aerodynamics Conference, 2006 [Google Scholar]
- Shen Guangchen, Bai Junqiang, Liu Nan, et al. Mechanical Simulation and Aerodynamic Analysis on a New Type of Wing Trailing Edge Variable Camber[J]. Journal of Northwestern Polytechnical University, 2016, 34(4): 578-586 (in Chinese) [Article] [Google Scholar]
- Rozhdestvensky K V. Aerodynamics of a Lifting System in Extreme Ground Effect[M]. Springer, Berlin Heidelberg, 2000 [CrossRef] [Google Scholar]
- Melvin A, Martinelli L. Aerodynamic Shape Optimization of Multi-Element Airfoils in Ground Effect[C]//AIAA Aerospace Sciences Meeting and Exhibit, 2008 [Google Scholar]
- Ahmed M R, Takasaki T, Kohama Y. Aerodynamics of a NACA4412 Airfoil in Ground Effect[J]. AIAA Journal, 2007, 45(1): 37-47 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Qin Xuguo, Liu Peiqing, Qu Qiulin, et al. Numerical Simulation and Analysis on Aerodynamics of Three-Element Airfoil in Ground Effect[J]. Journal of Aerospace Power, 2011, 26(4): 890-897 (in Chinese) [Article] [Google Scholar]
- Hsiun C M, Chen C K. Aerodynamic Characteristics of a Two Dimensional Airfoil with Ground Effect[J]. Journal of Aircraft, 1996, 33(2): 386-392 [Article] [CrossRef] [Google Scholar]
- Qu Q L, Wang W, Liu P, et al. Airfoil Aerodynamics in Ground Effect for Wide Range of Angles of Attack[J]. AIAA Journal, 2015, 53(4): 1-14 [Article] [CrossRef] [Google Scholar]
- Qu Q L, Wang W, Liu P, et al. Aerodynamics and Flow Mechanics of a Two-Element Airfoil in Ground Effect[C]//AIAA Aerospace Sciences Meeting, 2015 [Google Scholar]
- He Yuwei, Li Yalin, Zheng Longqian. Numerical Simulation on Aerodynamics of Three-Element Airfoil in Ground Effect[J]. China Science and Technology Review, 2012(9): 100-102 (in Chinese) [Article] [Google Scholar]
- Qu Q L, Huang L, Liu P, et al. Numerical Study of Aerodynamics and Flow Physics of the 30P30N Three-Element Airfoil in Dynamic Ground Effect[C]//AIAA Applied Aerodynamics Conference. 2016 [Google Scholar]
- Rumsey C L, Ying S X. Prediction of High Lift:Review of Present CFD Capability[J]. Progress in Aerospace Sciences, 2002, 38(2): 145-180 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Menter F R. Zonal Two-Equation K-W Turbulence Model for Aerodynamic Flows[R]. AIAA-1933-2906 [Google Scholar]
- Catalano P, Amato M. An evaluation of RANS Turbulence Modelling for Aerodynamic Applications[J]. Aerospace Science & Technology, 2003, 7(7): 493-509 [Article] [CrossRef] [Google Scholar]
- Eliasson P, Catalano P, Pape M C L, et al. Improved CFD Predictions for High Lift Flows in the European Project EUROLIFT Ⅱ[C]//AIAA Applied Aerodynamics Conference, 2007 [Google Scholar]
- Zerihan J, Zhang X. Aerodynamics of a Single Element wing in Ground Effect[J]. Journal of Aircraft, 2000, 37(6): 1058-1064 [Article] [CrossRef] [Google Scholar]
- Moir I R M. Measurements on a Two-Dimensional Aerofoil with High-Lift Devices: a Selection of Experimental Test Cases for the Validation of CFD Codes[R]. AGARD-AR-303, 1994 [Google Scholar]
- Fejtek I. Summary of Code Validation Results for a Multiple Element Airfoil Test Case[C]//European Conference on Information Systems, 2013: 422-432 [Google Scholar]
- Smith A M O. High-Lift Aerodynamic[J]. Journal of Aircraft, 1975, 12(6): 501-530 [Article] [CrossRef] [Google Scholar]
All Figures
 |
图1 多段翼型地面效应示意图 |
| In the text | |
 |
图2 多段翼型地面效应计算网格 |
| In the text | |
 |
图3 Tyrell-026构型及计算结果 |
| In the text | |
 |
图4 L1T2网格及计算结果 |
| In the text | |
 |
图5 地面效应下不同迎角的气动力系数 |
| In the text | |
 |
图6 翼型表面压力系数随离地高度的变化 |
| In the text | |
 |
图7 α=8°时主翼驻点处流线速度矢量角随离地高度的变化 |
| In the text | |
 |
图8 α=8°时不同离地高度下速度型测量位置和速度型对比 |
| In the text | |
 |
图9 巡航构型示意图 |
| In the text | |
 |
图10 巡航翼型不同迎角下总的升力系数和上下翼面的升力系数随离地高度的变化 |
| In the text | |
 |
图11 巡航翼型不同迎角下总的升力系数差量和上下翼面的升力系数差量随离地高度的变化 |
| In the text | |
 |
图12 多段翼型主翼不同迎角下总的升力系数差量和上下翼面的升力系数差量随离地高度的变化 |
| In the text | |
 |
图13 α=8°时扰流板不偏和下偏的多段翼型升力系数及其差量随离地高度的变化 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


