| Issue |
JNWPU
Volume 37, Number 4, August 2019
|
|
|---|---|---|
| Page(s) | 673 - 681 | |
| DOI | https://doi.org/10.1051/jnwpu/20193740673 | |
| Published online | 23 September 2019 | |
Relative Motion Dynamics Modeling and Control of DFP Vibration Isolation Spacecraft
基于螺旋理论的DFP隔振航天器相对运动动力学建模与姿轨耦合控制
1
School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China
2
National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China
Received:
10
September
2018
In order to better meet the future high precision task requirements, the DFP(Disturbance-Free Payload) spacecraft composed of non-contact PM(Payload Module)and SM(Support Module)is taken as the object to study the relative motion dynamics modeling and control between the two modules and verify the system vibration isolation performance. Firstly, the force and torque expressions of the two modules are derived by simplifying the configuration and analyzing the stress. In view of that couple effect, the relative motion dynamics equations between two modules of DFP spacecraft with high model accuracy, and simple and uniform format are established with the dual quaternions. Based on this, the PD control law is designed, and the relative motion of PM and SM could meet DFP spacecraft working requirements when the measurability of control quantity and the measurement error of sensors were taken into account. Simulation results verify the advantage of vibration isolation and attitude maneuverability of DFP spacecraft.
摘要
为更好满足未来高精度任务要求，以由无接触的有效载荷模块（payload module，PM）和支持模块（support module，SM）组成的DFP（disturbance-free payload）航天器为对象，开展两模块间的相对运动动力学建模与控制研究和系统隔振性能验证。首先通过简化构型、梳理受力情况，重点推导了两模块所受力和力矩表达式；其次考虑耦合效应，利用对偶四元数建立了模型精度更高且形式简洁统一的DFP航天器两模块间的相对运动动力学方程；在此基础上设计PD控制律，考虑控制量可测性及敏感器测量误差，使PM和SM的相对运动满足DFP航天器工作要求。仿真结果验证了DFP航天器的隔振优势和姿态机动性能。
Key words: DFP spacecraft / dual quaternions / relative motion dynamics modeling / PD control / vibration isolation / simulation / measurement error of sensors
关键字 : DFP航天器 / 对偶四元数 / 相对运动动力学建模 / PD控制
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
随着航天技术的发展, 一些太空任务对航天器的指向精度和运行稳定性提出了更高的要求。然而航天器上的活动部件(如飞轮、推力器等)和挠性部件(如太阳帆板、大型展开天线等)引发的平台干扰[1-2], 是制约指向精度的主要因素。虽然现阶段的隔振方案能在一定程度上抑制振动干扰, 但同时也充当了传播途径, 使振动隔而不绝[3]。而且发射成本较高, 当振源较多时, 效率低下。
洛克希德马丁公司于2003年提出了DFP系统的概念[4], 其核心思想是将航天器划分为有效载荷模块(payload module, PM)和支持模块(support module, SM)。具有高精度指向要求的设备(如空间相机、遥感设备等)安装于PM上, 构成超静平台; 对指向精度要求不高的设备和振源安装于SM上。通过其间的无接触执行机构控制PM完成高精度指向并隔离来自SM的振动, 同时为了满足无接触执行机构的工作要求, 也需SM快速跟踪PM运动。所以存在有两模块间的相互作用力和力矩, 动力学特性和控制回路显得更为复杂。因此有必要对DFP航天器模块间的六自由度相对运动建模与控制进行研究。
马明阳[1]根据DFP航天器原理, 设计了双体卫星的地面试验系统, 并对隔振效能进行了研究分析。张伟, 赵艳彬等[2]提出了一种振源与载荷在空间上完全隔离、对载荷舱进行主动控制, 服务舱跟随载荷舱从动控制的主从协同的卫星平台设计方法。杜超[3]以最大限度降低力执行器的静态耦合为原则, 设计了8个力执行器的空间分布方式, 进一步研究了控制力的分配问题和控制系统间的耦合问题。Nelson Pedreiro等[4-7]介绍了DFP航天器的概念及工作原理, 并通过系统级的硬件演示成功验证了其实施方案和性能。黄思萌[8]研究了基于DFP系统的航天器快速机动技术, 讨论了转动惯量存在不确定性时的控制问题及避免模块碰撞的策略。孔宪仁等[9]考虑立方构型的DFP接口, 建立两模块的相对运动动力学模型并通过比例微分控制方法设计了控制律, 仿真结果表明可以通过控制保证航天器的正常运行。
综上可以看出, 国内外研究都较多地集中于DFP航天器的性能验证及样机制造, 而关于PM相对于参考轨道坐标系、SM相对于PM的相对运动动力学模型的研究比较欠缺。即使有所涉及, 也都采用了传统的相对运动建模方法, 没有考虑相对姿态运动对相对平动的影响, 导致模型精度和控制精度较差。
本文以DFP航天器为对象, 考虑2个模块受到的作用力和力矩特性及其相对运动动力学的姿轨耦合特性, 进行建模与控制方法研究, 以期得到两模块间相对平动与相对姿态运动模型的统一表达式, 并实现存在测量、估计误差以及振动干扰的情况下姿轨耦合的精确控制。
1 构型简化和力学分析
1.1 坐标系定义
本文所涉及的研究对象包括PM、SM、对地定向时的参考以及惯性空间参考。故需给出对应的4个坐标系:地心惯性系坐标系OIXIYIZI、航天器轨道坐标系OLXLYLZL(可参考图 1)、PM本体坐标系OPXPYPZP和SM本体坐标系OSXSYSZS, 两本体系原点均位于模块质心, 三轴分别沿主惯量轴方向(可参考图 2)。
 |
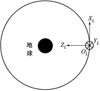图1 航天器轨道坐标系 |
1.2 构型简化
由于不讨论两模块的具体构型设计以及特殊构型(可表现为航天器惯性张量的变化)对运动特性的影响。因此为简便分析起见, 用2个圆柱体来近似表示PM和SM。采取3对六杆均匀分布, 且每对杆成正交关系的类立方Stewart平台式无接触执行机构空间布局[8](可参考图 2)。其中数字1~6表示无接触执行机构与PM铰接点的编号, 数字1′~6′表示无接触执行机构与SM铰接点的编号, hp和hs分别表示PM和SM的高, α为SM上2个铰接点1′, 2′(或3′, 4′或5′, 6′)与OS在SM上底面投影点连线的夹角。
设rP为PM半径, rS为SM半径, L0为无接触执行机构的标称长度, Γ0为两模块质心间的标称距离。则根据几何关系
用riP(i=1, 2, 3, 4, 5, 6)表示在PM本体系下描述的PM上各铰接点相对于PM质心的位置矢量, 用riS (i=1, 2, 3, 4, 5, 6)表示在SM本体系下描述的SM上各铰接点相对于SM质心的位置矢量, 则
1.3 受力分析
1.3.1 无接触执行机构的影响
DFP航天器中所使用的无接触执行机构一般为音圈电机, 其工作原理可参考文献[10]。这里可以不失合理性地将其看作一根可产生轴向无时延力的无接触直杆。
无接触执行机构长度矢量在PM本体系下表示为liP(i=1, 2, 3, 4, 5, 6), 其与PM本体坐标系、SM本体坐标系的空间位置关系如图 3所示。用L1S表示SM质心相对于PM质心在SM本体坐标系下描述的位置矢量, 则
式中，ASP表示由SM本体坐标系到PM本体坐标系的姿态转换矩阵。可以看出, 在各铰接点位置和两模块尺寸给出的情况下, 无接触执行机构长度矢量由PM和SM的相对位姿唯一确定。
设kiP为liP的单位矢量, 则PM与SM受到的无接触执行机构作用力和力矩在各自本体坐标系下可表示为
式中
均为6×6阶方阵; APS表示由PM本体坐标系到SM本体坐标系的姿态转换矩阵; fi(i=1, 2, 3, 4, 5, 6)为无接触执行机构轴向力的模值。
f=[f1 f2 f3 f4 f5 f6]T, 表示6个无接触执行机构产生的力矢量, (ri)×表示矢量ri的叉乘矩阵, 具体形式为
 |
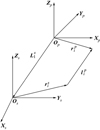图3 无接触执行机构长度矢量与PM/SM本体坐标系的空间位置关系 |
1.3.2 地球引力场的影响
作用在PM和SM上的地球引力和重力梯度力矩分别在各自本体坐标系下表示为
式中，mP, mS分别为PM和SM的质量; JP, JS分别为PM和SM的惯性张量矩阵; rgP, rgS分别为PM和SM质心到地心的位置矢量在各自本体坐标系下表示, 且rgS=APSrgP+L1S。
1.3.3 飞轮的影响
设SM的绝对角速度在其本体坐标系下表示为ωS/IS。飞轮惯性张量矩阵为JF, 相对于星体的转动角速度为ωFS, 则
式中, TW为外力矩矢量。
另考虑作用在SM上由飞轮动静不平衡引起的干扰力矩, 设3个方向的飞轮正交安装, 且参数相同, 飞轮轴线分别与SM本体坐标系的3个坐标轴重合。则干扰力矩表达式可写作[9]
式中, hk为第k个谐波频率与飞轮转速之比; K为谐波数; ωx, ωy和ωz分别为3个方向上飞轮的转速; Ck为动静不平衡系数; Tdx, Tdy和Tdz分别为3个方向上的干扰力矩。
2 相对运动动力学建模
传统建模方法虽然可以反映运动本质, 却是不甚精确的。而对偶四元数可以将姿轨方程统一表达, 展现了一定的优势。因此为了提高控制精度, 有必要对基于对偶四元数的相对运动动力学建模方法进行研究[11-13], 并将其用于建立DFP航天器相对运动模型。
1) 为了验证PM的姿态机动能力和对地定向能力, 建立PM相对于参考轨道坐标系的相对运动动力学方程, 并表示在PM本体坐标系中
式中
为PM的绝对对偶速度; 
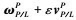为PM相对于航天器轨道坐标系的对偶速度; 
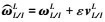为航天器轨道坐标系相对地心惯性坐标系的对偶速度; 
为PM本体坐标系相对于航天器轨道坐标系的对偶四元数;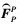 
为作用在PM上的对偶力, 包括对偶控制力、对偶重力和对偶干扰力。
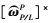为叉乘矩阵。
2) 为了验证SM对PM的跟随能力, 建立SM相对于PM的相对运动动力学方程, 并表示在SM本体坐标系中
式中
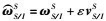为SM绝对对偶速度;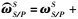 
为SM相对于PM的对偶速度; 
为SM本体坐标系相对于PM本体坐标系的对偶四元数;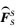 
为作用在SM上的对偶力, 包括对偶控制力、对偶重力和对偶干扰力。
为叉乘矩阵。
另可将(12)式写作
当不存在控制力偏心的情况下, (13)式中第一式不包含轨道参数, 相对平动对相对姿态运动没有影响。第二式包含ωS/IS, ωP/IS, ωS/PS的叉乘项, 说明PM和SM的绝对角速度以及两者的相对角速度均会对相对平动产生影响, 存在姿轨耦合; 如果发生控制力偏心, 那么在进行轨控时一方面会造成相对姿态的变化, 另一方面相对姿态变化也会通过叉乘项影响相对平动, 此时姿轨也会发生耦合。
3 PD控制系统设计
图 4所示控制系统包含3条回路:①PM姿态控制；②PM和SM相对姿态控制；③PM和SM相对平移控制。
用无接触执行机构进行PM姿态控制和相对平动控制, 用外部执行机构进行相对姿态控制。在这种情况下, 进行相对平动控制的无接触执行机构产生所需的过质心的力, 该力对PM力矩为零, 也就是说不影响PM姿态。通常可应用在对姿态控制要求远高于平动控制要求的情况中。基于以上分析, 从控制的实用性、简洁性以及可靠性角度出发, 设计了基于对偶四元数的PM相对于参考轨道坐标系、SM相对于PM的PD控制律。
 |
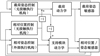图4 DFP航天器控制系统框图 |
3.1 PM相对于参考轨道坐标系的相对运动控制律
不考虑相对平动控制的情况下, 给出PM相对于参考轨道坐标系的相对运动控制律
kp1和kD1为控制参数; qe*和ωP/LP*为PM相对于参考轨道坐标系的期望四元数和角速度, 
和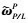
为实际测量得到的四元数和角速度。
3.2 SM相对于PM的相对运动控制律
为保持要求的相对位姿, 设计SM相对于PM的姿轨一体化相对运动控制律
kp2和kD2为控制参数; 
和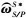
为SM相对于PM的期望对偶四元数和对偶角速度, 
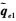和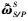
为测量估计的对偶四元数和对偶角速度; TYS为无接触执行机构对SM的干扰力矩。
根据(14)式可以得到无接触执行机构需对PM作用的合控制力矩; 根据(15)式可以得到无接触执行机构需产生的合控制力。将两者带入(6)式, 便能反解出无接触执行机构的力矢量。同时, (15)式也指示了为满足模块间相对姿态要求, 外部执行机构需产生的控制力矩。
3.3 PM和SM的相对运动信息估计
PM和SM间的相对运动信息必须通过无接触位移敏感器和无接触速度敏感器测量无接触执行机构长度的变化情况估计获得, 下面将详细介绍这一过程。
设PM本体坐标系与SM本体坐标系间某一时刻的相对姿态角分别为φ1(滚转角)、θ1(俯仰角)、ψ1(偏航角), 标称状态下的相对姿态角分别为φ0、θ0、ψ0。由于SM的快速机动性很好, 所以Δφ=φ1-φ0, Δθ=θ1-θ0, Δψ=ψ1-ψ0都可看作小量, 即
1) cosΔφ≈cosΔθ≈cosΔψ≈1
2) 二阶及二阶以上小量看作0。
所以PM本体系到SM本体系的姿态转换矩阵简化为
如果此时两模块的相对位置矢量为L1S=(L1xS L1yS L1zS), 则无接触执行机构对应时刻的长度
这是一个很难求解的非线性方程, 因此必须进行线性化。观察(17)式, 在无接触执行机构安装位置及PM、SM尺寸已知情况下, li(i=1, 2, 3, 4, 5, 6)是关于φ1, θ1, ψ1, L1xS, L1yS和L1zS的函数。将其在标称状态ϕ0=0, θ0=0, ψ0=0, L10S=(0 0 -Γ0)附近展开, 得到
共有6个方程, 6个未知数, 可以求解。最终得到估计的相对位置和相对姿态
对(17)式两边求导
由于相对姿态和相对位置已经估计出来, 意味着方程组(20)的系数矩阵也已知晓。6个方程6个未知量, 可求得
和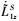
。进一步得到相对角速度和相对速度的估计量
由于用到泰勒公式进行方程的线性化, 忽略了二阶及以上小量, 故而会产生一部分估计误差。另外敏感器工作过程中存在的测量误差, 也会导致估值的不准确。
4 数值仿真
根据前面建立的相对运动动力学模型及控制律, 对DFP航天器的对地定向和姿态机动过程进行仿真。航天器结构参数如表 1所示, 控制参数如表 2所示, 初始状态参数如表 3所示。
考虑飞轮动静不平衡力矩时, 设3个飞轮初始转速均取600 rad/s。其他参数数值见表 4[9]。
航天器上搭载的各类敏感器测量误差数据在表 5中给出。
衡量仿真结果是否达到要求的指标主要有:
1) 观察PM的姿态是否达到并稳定在期望值附近;
2) SM和PM的相对位姿是否保持在标称状态附近;
3) 无接触执行机构的长度变化是否超出5 mm的正常工作范围。
DFP航天器结构参数
控制参数
初始状态参数
干扰力矩数学模型参数
各类敏感器测量误差
4.1 PM对地定向仿真
基于以上仿真参数, PM对地定向仿真结果如下:图 5表示对地定向时PM的姿态角变化曲线, 图 6表示PM与SM的相对姿态角变化曲线。可以看出存在飞轮干扰力矩的情况下, SM指向精度约为5.4×10-3/(°), PM指向精度约为5×10-5/(°), 高出SM指向精度2个量级, 说明两模块间的机械解耦设计非常有效地隔离了振动干扰。图 7展示了PM与SM的相对位置变化情况, 观察可知两者相对位置都很好地保持在标称附近, 偏差不超过0.04 mm。由图 8知, 无接触执行机构长度变化不超过0.04 mm, 保持在合理范围内。
 |
图5 PM姿态角 |
 |
图6 PM与SM相对姿态角 |
 |
图7 PM与SM的相对位置 |
 |
图8 无接触执行机构长度变化量 |
4.2 PM姿态机动仿真
基于以上仿真参数, PM姿态机动仿真结果如下:图 9展示了PM机动时的姿态变化, 经过30 s左右从初始状态改变为(0.1 0.2 -0.15)T rad。同时图 10给出了SM与PM的相对姿态变化, 3个相对姿态角均保持在10-3rad量级, 说明在PM机动的同时, SM也进行了相等幅度的快速机动, 这不仅验证了DFP航天器良好的机动性能, 也佐证了前面小角度假设的正确性。图 11给出了PM和SM的相对位置变化情况, 可以看出两者相对位置保持在(0 0 -445.2)T mm左右, 最大偏差不超过1.5 mm。图 12给出了无接触执行机构长度的变化情况, 可以看出, 最大偏差不到5 mm, 符合结构要求。
 |
图9 PM姿态角 |
 |
图10 PM与SM相对姿态角 |
 |
图11 无接触执行机构长度变化量 |
5 结论
本文针对传统动力学建模方法存在的模型不精确、姿轨方程形式不统一的问题, 利用对偶四元数建立了DFP航天器的PM相对于轨道坐标系、SM相对于PM的相对运动动力学模型。并在考虑测量、估计误差以及振动干扰的情况下, 设计姿轨一体的PD控制律, 通过仿真验证了DFP航天器优秀的隔振性能和姿态机动能力。充分说明更精确的相对运动建模方法对研究DFP航天器具有重要意义。为未来可能应用DFP航天器模式的先进航天器的设计过程提供了参考。
References
- Ma Yangming. The Design and Analysis on Vabration Isolation Efficiency of a Satellte Test System with Architecture of Disturbance Free Payload[D]. Habrbin, Harbin Institute of Technology, 2016 (In chinese) [Google Scholar]
- Zhang Wei, Zhao Yanbin, Liao He, et al. Design of Active-Quiet Isolated and Master-Slave Coordination Controlled Dual-Super Satellite Platform[J]. Aerospace Shanghai, 2014, 31(5): 7–11 [Article] (In chinese) [Google Scholar]
- Du Chao. Study on Dynamic Modeling and Controlling of a Satellite with a Architectrue of Disturbance Free Payload[D]. Harbin, Harbin Institute of Technology, 2015 (In chinese) [Google Scholar]
- Pedreiro N. Spacecraft Architecture for Disturbance Free Payload[J]. Journal of Guidance Control and Dynamics, 2002, 26(5): 794–804 [Article]">10.3969/j.issn.1006-1630.2014.05.002 [NASA ADS] [CrossRef] [Google Scholar]
- Pedreiro N, Carrier A, Lorell K, et al. Disturbance Free Payload Concept Demonstration[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, USA, 2002 [Article] [Google Scholar]
- Gonzales M, Pedreiro N, Brookes K, et al. Unprecedented Vibration Isolation Demonstration Using the Disturbance Free Payload Concept[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, USA, 2004 [Article] [Google Scholar]
- Pedreiro N, Gonzales M, Foster B, et al. Agile Disturbance Free Payload[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, USA, 2005 [Article] [Google Scholar]
- Huang Simeng. Research on Agile Technologies of Three-Rigid-Body Spacecraft Based on DFP System[D]. Harbin, Harbin Institute of Technology, 2016 (In chinese) [Google Scholar]
- Kong Xianren, Wu Chen, Liu Yuan, et al. Dynamic Modeling of Relative Motion for Disturbance-Free-Payload Spacecraft[J]. Journal of Astronautics, 2017, 38(11): 1139–1146 [Article] (In chinese) [Google Scholar]
- Zhang Dawei, Feng Xiaomei. The Technical Principle of Voice-Coil Actuator[J]. Journal of North University of China, 2006(3): 224–228 [Article] (In chinese) [Google Scholar]
- Liu Jian, Zhu Zhanxia, Ma Jiajin. Establishing Spacecraft's Relative Orbit and Attitude Coupling Dynamics Model Based on Screw Theory[J]. Journal of Northwestern Polytechnical University, 2013, 31(4): 590–595 [Article] (In chinese) [Google Scholar]
- Zhu Zhanxia, Ma Jiajin, Fan Ruishan. Coupling Analysis on Relative Motion of Spacecraft Attitude and Orbit Model Based on Dual Quaternion[J]. Journal of Northwestern Polytechnical University, 2015, 33(6): 887–891 [Article] (In chinese) [Google Scholar]
- Zhu Zhanxia, Ma Jiajin, Fan Ruishan. Synchronization Control of Relative Motion for Spacecraft with Screw Theory-Based Description[J]. Acta Aeronautical et Astronautica Sinica, 2016, 37(9): 2788–2798 [Article] (In chinese) [Google Scholar]
All Tables
All Figures
|
图1 航天器轨道坐标系 |
| In the text | |
 |
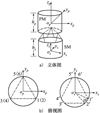图2 DFP航天器构型[8] |
| In the text | |
|
图3 无接触执行机构长度矢量与PM/SM本体坐标系的空间位置关系 |
| In the text | |
|
图4 DFP航天器控制系统框图 |
| In the text | |
|
图5 PM姿态角 |
| In the text | |
|
图6 PM与SM相对姿态角 |
| In the text | |
|
图7 PM与SM的相对位置 |
| In the text | |
|
图8 无接触执行机构长度变化量 |
| In the text | |
|
图9 PM姿态角 |
| In the text | |
|
图10 PM与SM相对姿态角 |
| In the text | |
|
图11 无接触执行机构长度变化量 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.