| Issue |
JNWPU
Volume 38, Number 5, October 2020
|
|
|---|---|---|
| Page(s) | 994 - 1000 | |
| DOI | https://doi.org/10.1051/jnwpu/20203850994 | |
| Published online | 08 December 2020 | |
Research on Dynamic Characteristic of Rudder Transmission System with Multiple Clearance Joints
含多个间隙铰的舵机传动系统动力学特性研究
1
Shaanxi Engineering Laboratory for Transmissions and Controls, Northwestern Polytechnical University, Xi'an 710072, China
2
China Academy of Launch Vehicle Technology, Beijing 100076, China
Received:
16
December
2019
In order to meet the characteristics including small clearance, heavy load and large contact area of joints existed in rudder transmission system, a new normal contact force model is established, which is suitable for the large-area contact process and considers the coefficient of nonlinear variable stiffness as well as the axial length of bearing. The applicability of this model is verified by simulations under some conditions with different clearance size, restitution coefficient, initial collision speed and bearing's axial length. Furthermore, through the user-defined subroutine interface in ADAMS software, this modified contact force model is compiled and linked into the dynamic model of the rudder transmission system. The simulation results show that the dynamic response of the system with multiple clearance joints is not a simple superposition of that with one single clearance, and the dynamic interaction between these joints intensifies the oscillation and nonlinear characteristics of the system. This study provides a theoretical reference for the structural optimization and control strategy design of aircraft with clearance joints.
摘要
为了满足舵机传动系统中铰链小间隙、大力载和大接触区域的特点,建立了一种适用于大面积接触碰撞过程且考虑非线性变刚度系数和轴承轴向尺寸的法向接触力模型。通过在不同间隙尺寸、恢复因数、初始碰撞速度和轴承轴向尺寸等各种工况下的仿真分析,验证模型的适用范围。进一步通过ADAMS软件中用户自定义子程序接口,将该接触力模型通过编译、链接嵌入舵机传动系统的动力学模型中,仿真结果表明:多个间隙铰下的系统动态响应并非单个间隙下响应的简单叠加,其相互耦合作用加剧了系统的振荡及非线性特性。该研究为含间隙铰飞行器的结构优化及控制策略设计提供理论参考。
Key words: rudder transmission system / clearance joint / nonlinear contact force model / dynamic interaction / simulation / ADAMS
关键字 : 舵机传动系统 / 间隙铰 / 非线性接触力模型 / 动力学相互作用
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
舵机传动系统目前广泛应用于飞机、运载火箭、导弹、卫星等飞行器控制领域,是一种高精度位置伺服系统,通常由舵机、传动机构、舵面及控制系统组成[1],舵机接受舵面偏转信号输出控制指令,经过传动机构改变舵偏角,控制飞行器的飞行姿态或飞行轨迹,使飞行器按照预定目标稳定地飞行。其中,传动机构可视作含多铰链间隙的非线性多体连接机构,其准确性和精密性直接影响了飞行器的飞行轨迹精度和动态品质。
实际工程中,由于动配合、材料变形、装配和磨损等原因,间隙是不可避免的,即使很小的间隙也会导致系统产生振动、噪音和磨损现象。Li等针对太阳帆板展开机构进行了建模、间隙-柔性耦合、间隙-热-结构耦合等研究,研究结果为含间隙铰航天器动态行为预测与控制奠定理论基础[2];Bai等研究了铰链间隙对卫星天线双轴定位机构运动学和动力学特性的影响,并提出一种优化设计方法以降低间隙对空间机构的冲击[3];闫绍泽等以空间可展机构为研究对象,研究了间隙、摩擦、重力、柔性等多参数对系统动态性能的影响[4]及间隙非线性等问题[5]。随着对飞行器性能要求的日益提高,研究间隙对舵面传动系统动力学行为的影响迫在眉睫。
由于建立合适有效的接触力模型对精确建模、分析含间隙铰多体动力学行为至关重要[6],因此本文以舵机传动系统为研究对象,鉴于其应用场合的特殊性,提出改进的法向接触力模型以模拟间隙铰的接触碰撞过程,并通过不同工况下的仿真分析验证该模型的适用范围。最后,综合分析了不同间隙铰数量对舵机传动系统动力学特性的影响规律,探究不同间隙铰间的动力学相互作用。
1 间隙铰数学模型
将旋转铰间隙引入多体系统动力学模型中是求解含间隙系统动力学的关键,通常通过间隙矢量模型来描述轴与轴承接触碰撞过程中的相对运动关系与相对位置变化。图 1表示多体系统中的旋转间隙铰模型, 其中e为间隙矢量, 其通过连接轴承中心CB与轴中心CJ表示
式中, rBO和rJO分别为轴承中心CB与轴中心CJ在广义坐标系XOY下的位置矢量。
间隙矢量e的大小可称为偏心距, 其表达式为
图 1b)为多体系统中间隙铰链处碰撞模型。当轴和轴承发生接触碰撞时, 碰撞点处的法向单位矢量可用间隙矢量表示为
碰撞点处的切向单位矢量t可由法向单位矢量逆时针旋转90°得到。
如图 1b)所示, 当多体系统间隙铰链处于接触碰撞状态时, 接触碰撞点处的弹性变形量矢量δ可表示为[6, 10]
式中, rBP和rJP分别为接触时轴承接触点PB和轴接触点PJ在广义坐标系下的位置矢量。
弹性变形量矢量δ的大小可以通过轴、轴承接触碰撞时的偏心距e和间隙c得到
接触点的法向碰撞速度vn和切向碰撞速度vt用以计算间隙铰链在接触碰撞过程中的能量损失, 可以表示为
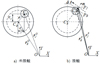 |
图1 多体系统中间隙铰模型 |
2 接触力模型
当轴与轴承发生接触碰撞时, 接触力Fc沿接触点的法向方向n和切向方向t分解为法向接触力Fn和切向接触力Ft(也称为摩擦力)。
2.1 法向接触力模型
由于舵机传动系统应用场合的特殊性, 其铰链具有小间隙、大力载、大接触区域的特点, 且接触刚度随接触深度的变化而时刻变化[7], 因此, 建立一种适用于舵机传动系统回转铰链的非线性法向接触力模型非常必要。
现有的含间隙铰链处法向接触力模型主要基于Hertz接触理论, 其中L-N模型应用最为广泛[8], 而Liu指出L-N模型仅适用于大间隙、小载荷工况下恢复因数接近1的非协调接触问题[9]。针对该模型的不足, 本文结合Gonthier模型适用于大面积接触碰撞过程的特点[10]和王旭鹏模型考虑非线性变刚度系数和轴承轴向尺寸的优势[11], 提出一种改进的非线性法向接触力模型, 其可以考虑触碰撞过程几何形状、材料特性、轴承轴向尺寸、碰撞过程能量损耗等因素, 且不受恢复因数限制并适用于大面积接触碰撞过程, 表达式为
式中:FN为接触力; δ为轴与轴承的相对接触深度; E*为等效弹性模量, 其表达式如(9)式所示; c为径向半径间隙; cr为恢复因数; (-)为初始碰撞速度; L为轴承轴向尺寸; n为非线性力指数, 对于金属材料通常取1.5。
式中:EB和EJ分别为轴承和轴的弹性模量; νB和νJ分别为轴承和轴的泊松比。
为了验证该模型的适用性, 以含间隙铰链中轴和轴承的一次碰撞为例, 分析改进的非线性接触力模型在不同间隙尺寸、不同恢复因数、不同初始碰撞速度和不同轴承轴向尺寸等各种工况下的有效性。轴承半径为10 mm, 轴和轴承材料相同, 弹性模量均为207 GPa, 泊松比均为0.3, 轴质量为1 kg。
1)不同间隙尺寸
分别取间隙尺寸为0.01 mm, 0.1 mm, 0.3 mm和0.5 mm, 初始相对碰撞速度为0.5 m/s, 恢复因数为0.7, 轴承轴向尺寸为15 mm进行仿真分析, 结果如图 2及表 1所示。结果表明:不同间隙尺寸下的接触力和接触深度在接触和分离的过程是非对称的, 且随着间隙尺寸的增大非对称性越明显; 间隙越大, 最大接触深度越大, 而最大接触力越小, 接触力达到最大时的时刻与接触深度达到最大时的时刻均增大; 不同间隙下的轴-轴承碰撞后分离速度不变, 且基于改进的非线性接触力模型所得到实际接触时的恢复因数与理想恢复因数的误差均为4.286%, 误差可控制在10%以内, 即表示该模型不受间隙大小的限制且恢复因数误差不受间隙大小的影响。
2) 不同恢复因数
分别取恢复因数为0.3~1, 间隙尺寸为0.1 mm, 初始相对碰撞速度为0.5 m/s, 轴承轴向尺寸为15 mm进行仿真分析, 结果如图 3及表 1所示。
结果表明:恢复因数越大, 最大接触深度越大, 接触力达到最大时的时刻与接触深度达到最大时的时刻越大, 其原因为:恢复因数越大, 系统能量损耗越小, 使得能量损耗较慢, 由图 3a)中接触和分离阶段包含的封闭环区域面积可看出这一现象, 从而达到最大接触力和最大接触深度的时间越长; 恢复因数越大, 碰撞恢复过程越快, 整体接触碰撞过程时间越短, 该现象由表 1中可看出; 基于改进的非线性接触力模型所得到不同恢复因数下的实际恢复因数与理想恢复因数的误差均控制在10%以内, 即表明该模型不受恢复因数大小的限制。
3) 不同初始碰撞速度
分别取初始碰撞速度0.5 m/s, 1 m/s, 3 m/s和5 m/s, 间隙尺寸为0.1 mm, 恢复因数为0.7, 轴承轴向尺寸为15 mm进行仿真分析, 结果如图 4及表 1所示。
结果表明:初始碰撞速度越大, 最大接触深度和最大接触力越大, 达到最大接触力和最大接触深度的时间越短, 而完成一次接触碰撞过程所需时间越少; 不同初始碰撞速度下的系统实际恢复因数相同, 即系统恢复因数不受初始碰撞速度影响, 与恢复因数为系统固有属性且仅与碰撞体材料相关这一特点相符。
4) 不同轴承轴向尺寸
分别取不同轴承轴向尺寸为5 mm, 10 mm, 15 mm和20 mm, 间隙尺寸为0.1 mm, 初始碰撞速度0.5 m/s, 恢复因数为0.7进行仿真分析, 结果如图 5及表 1所示。
结果表明:不同轴承轴向尺寸下的系统接触碰撞过程不同; 轴承轴向尺寸越大, 最大接触深度越小, 最大接触力越大, 达到最大接触力和最大接触深度的时间越短, 完成一次接触碰撞过程所需时间越少; 不同轴承轴向尺寸下的系统实际恢复因数相同, 且控制在10%内, 即该非线性接触力模型可较好地考虑碰撞体的轴向尺寸影响。
 |
图2 不同间隙尺寸仿真结果 |
不同工况仿真数据
 |
图3 不同恢复因数仿真结果 |
 |
图4 不同初始碰撞速度仿真结果 |
 |
图5 不同轴承轴向尺寸仿真结果 |
2.2 切向接触力模型
Coulomb摩擦模型是描述干接触表面之间最简单的摩擦模型。然而, 该摩擦模型可能导致数值积分上的困难。为了避免该问题, 众多学者对Coulomb摩擦模型进行了修正, 其中Ambrósio摩擦模型[12]被广泛应用
式中:cf为摩擦因数; cd为与切向速度vt相关的动态修正因数, 其表达式为
式中, v0和v1为给定的切向速度误差值。
3 数值计算
图 6为舵机传动系统动力学仿真模型, 包含4处铰链:作动杆-辅助摇臂(编号A)、辅助摇臂-辅助连杆(编号B)、辅助摇臂-轴承座3(编号C)和辅助连杆-摇臂(编号D)。基于用户自定义子程序模板, 在VS2010中修改接触力表达式, 并通过编译、链接等步骤生成动态链接库文件。通过Solver settings-Executable-Library将该动态链接库文件嵌入Adams中, 既避免了大型机构编程的复杂性, 且为后续实现刚柔耦合、刚-柔-热耦合等建模分析奠定基础。各构件材料如表 2所示, 仿真参数如表 3所示。仿真初始状态为摇臂中线垂直于地面90°, 仿真结果均为机构达到稳定状态后。
如图 7所示为考虑不同间隙铰个数时的舵轴角加速度曲线。不同工况下, 舵轴角加速度均围绕理想曲线上下波动, 不同之处在于当仅考虑A处铰链间隙时舵轴输出光滑波动, 而当考虑多个间隙铰时, 甚至是只有2个间隙时, 舵轴输出呈脉冲式响应; 随间隙铰个数增加, 舵轴输出曲线波动幅值急剧增加, 波动峰值分别为902.487 1°/s2, 2 482.806 7°/s2, 2 695.047 5°/s2和4 063.383 1°/s2, 其中工况2(考虑A, B处间隙)的波动峰值大于工况1(仅考虑A处间隙)波动峰值的2.5倍, 这也表明, 考虑2个间隙的系统响应并非只是含1个间隙时系统响应的简单叠加, 多个间隙铰间的相互作用使得系统响应愈发偏离理想输出, 该现象由图 8可进一步验证, 间隙铰之间的相互作用致使舵机传动系统动态响应的非线性特性愈发明显, 系统朝着混沌方向发展。
由图 7b)和图 7c)可分析得:工况2与工况3的舵轴角加速度曲线差别较小, 其原因在于C处铰链中的组成构件轴承座3固定于地面, 但由图 8b)和8c)仍可以观察到即使存在固定构件, 系统非线性特性仍随间隙铰个数增加而变强。由图 7中各种工况下的舵轴角加速度局部放大图可知, 每一次大脉冲下伴随多次小脉冲, 且随着间隙铰个数的增加, 小脉冲的次数增多, 即表明多个间隙铰间的相互作用加剧了轴与轴承间碰撞的强度和持续时间。
 |
图6 舵机传动系统动力学仿真模型 |
各构件材料参数
仿真参数
 |
图7 含不同间隙铰个数的舵轴角加速度 |
 |
图8 含不同间隙铰个数的舵轴角速度-角加速度相图 |
4 结论
为了满足舵机传动系统中回转铰链小间隙、大力载和大接触区域的特点,本文建立了一种可以考虑接触碰撞过程几何形状、材料特性、轴承轴向尺寸、碰撞过程能量损耗等因素,且不受恢复因数限制并适用于大面积接触碰撞过程的改进的非线性法向接触力模型。基于该改进模型,以舵面传动系统为研究对象,进行了不同间隙铰个数下的动力学仿真。研究结果表明:
1) 改进的非线性接触力模型适用于不同间隙尺寸、恢复因数、初始碰撞速度和轴承轴向尺寸等工况下的接触碰撞,误差均控制在10%以内,可以有效地描述铰链间隙对机构动态特性的影响;不同工况下的接触力和接触深度在接触和分离的过程是非对称的,且均是先达到最大接触力再达到最大接触深度;碰撞体在接触碰撞过程中的实际恢复因数与间隙尺寸、初始碰撞速度和轴承轴向尺寸无关。
2) 随着间隙铰数量的增多,舵轴角加速度波动幅值变大,响应呈脉冲式,且脉冲强度和持续时间增大;间隙铰间的相互作用加剧了系统的非线性特性,使系统趋于混沌。
References
- Arriola D, Thielecke F. Model-Based Design and Experimental Verification of a Monitoring Concept for an Active-Active Electromechanical Aileron Actuation System[J]. Mechanical Systems and Signal Processing, 2017, 94: 322–345 [Article] [CrossRef] [Google Scholar]
- Li Yuanyuan, Wang Cong, Huang Wenhu. Rigid-Flexible-Thermal Analysis of Planar Composite Solar Array with Clearance Joint Considering Torsional Spring, Latch Mechanism and Attitude Controller[J]. Nonlinear Dynamics, 2019, 96: 2031–2053 [Article] [CrossRef] [Google Scholar]
- Bai Zhengfeng, Zhao Jijun, Chen Jun, et al. Design Optimization of Dual-Axis Driving Mechanism for Satellite Antenna with Two Planar Revolute Clearance Joints[J]. Acta Astronautica, 2018, 144: 80–89 [Article] [CrossRef] [Google Scholar]
- Li Junlan, Yan Shaoze, Guo Feng, et al. Effects of Damping, Friction, Gravity, and Flexibility on the Dynamic Performance of a Deployable Mechanism with Clearance[J]. Journal of Mechanical Engineering Science, 2012, 227(8): 1791–1803 [Article] (in Chinese) [Google Scholar]
- Yan Shaoze. Development and Problems of Nonlinear Dynamics of the Mechanisms with Clearances for Spacecrafts[J]. Journal of Dynamics and Control, 2004, 2(2): 48–52 [Article] (in Chinese) [Google Scholar]
- Tan Haiyan, Hu Yujin, Li Li. A Continuous Analysis Method of Planar Rigid-Body Mechanical Systems with Two Revolute Clearance Joints[J]. Multibody System Dynamics, 2017, 40: 347–373 [Article] [CrossRef] [Google Scholar]
- Li Zhonghong. Dynamic Modeling and Analysis of Transmission Mechanism with Joint Clearances for Air Rudder[D]. Harbin, Harbin Institute of Technology, 2015(in Chinese) [Google Scholar]
- Lankarani H M, Nikravesh P E A Contact Force Model with Hysteresis Damping for Impact Analysis of Multibody Systems[J]. Journal of Mechanical Design, 1990, 112: 368–376 [Article] (in Chinese) [CrossRef] [Google Scholar]
- Liu C S, Zhang K, Yang R. The FEM Analysis and Approximate Model for Cylindrical Joints with Clearances[J]. Mechanism and Machine Theory, 2007, 42: 183–197 [Article] [CrossRef] [Google Scholar]
- Li Bo, Wang Sanmin, Yuan Ru, et al. Dynamics Analysis of Planar Linear Array Deployable Structures under the Coupling Action of Clearance Joints[J]. Journal of Northwestern Polytechnical University, 2017, 35(3): 455–461 [Article] (in Chinese) [Google Scholar]
- Wang Xupeng, Liu Geng, Ma Shangjun. Dynamic Analysis of Planar Mechanical Systems with Clearance Joints Using a New Nonlinear Contact Force Model[J]. Journal of Mechanical Science and Technology, 2016, 30(4): 1537–1545 [Article] [CrossRef] [Google Scholar]
- Ambrósio J A C. Impact of Rigid and Flexible Multibody Systems:Deformation Description and Contact Models[J]. Virtual Nonlinear Multibody Systems, 2002, 103: 57–81 [Article] (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 多体系统中间隙铰模型 |
| In the text | |
 |
图2 不同间隙尺寸仿真结果 |
| In the text | |
 |
图3 不同恢复因数仿真结果 |
| In the text | |
 |
图4 不同初始碰撞速度仿真结果 |
| In the text | |
 |
图5 不同轴承轴向尺寸仿真结果 |
| In the text | |
 |
图6 舵机传动系统动力学仿真模型 |
| In the text | |
 |
图7 含不同间隙铰个数的舵轴角加速度 |
| In the text | |
 |
图8 含不同间隙铰个数的舵轴角速度-角加速度相图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


