| Issue |
JNWPU
Volume 42, Number 3, June 2024
|
|
|---|---|---|
| Page(s) | 531 - 539 | |
| DOI | https://doi.org/10.1051/jnwpu/20244230531 | |
| Published online | 01 October 2024 | |
Study on multi-state of meshing-impacting dynamic characteristics of spur gear systems considering friction under localized tooth breakage
局部破损下考虑摩擦的直齿轮系统多状态啮合-碰撞动态特性研究
School of Mechanical Engineering, Lanzhou University of Technology, Lanzhou 730050, China
Received:
30
April
2023
Localized tooth breakage is one of the common failures of spur gears, which affects the smooth and safe operation of spur gear transmission systems. The tooth collision cannot be neglected, and it is especially important to reveal the meshing-impacting dynamic characteristics of the gear system under localized tooth breakage to improve the safe and stable operation of the gear system. Based on the gear meshing principle and the dissipative collision contact force model, the drive-side tooth meshing model and back-side tooth impacting model are established with considering the transient nature of tooth back-side contact. The tooth surface meshing model and tooth back collision model under partial breakage are established. According to the contact state and force environment of the gear pair, the multi-state meshing-impacting behaviour under local breakage is classified, and the discrete meshing-impact dynamics model of an involute spur gear system under local breakage is established to explore the influence of local breakage on the meshing stiffness and load distribution. The mechanism of contact force under partial tooth breakage is revealed, and the influence of load coefficient and meshing frequency on the nonlinear dynamics is studied by defining two Poincaré maps. It is found that local tooth breakage affects the contact force of single-and double-tooth meshes and reduces gear load carrying capacity. Larger loads inhibit back-side impact, and smaller loads induce the coexistence behaviour and back-side impact. Larger or smaller meshing frequency induce back-side impact behaviour. The coexistence of chaotic and periodic motions induces back-side impact behaviour, and localized tooth breakage affects the coexistence phenomenon and aggravates the complexity of the dynamic behaviour. The dynamic model of gear system considering energy dissipation and nonlinear vibration under the presence of local tooth breakage of the pinion is explored, and the conditions of back-side impact are studied. This research provides new methods and ideas for nonlinear dynamic modelling and analysis of faulty gear systems.
摘要
局部破损是直齿轮常见的故障之一, 影响齿轮传动的平稳、安全运行。轮齿碰撞不可忽略, 揭示局部破损下齿轮系统啮合-碰撞动态特性对提高齿轮系统安全稳定运行尤为重要。基于齿轮啮合原理和能量耗散碰撞接触力模型, 考虑齿背接触的瞬时性, 建立局部破损下齿面啮合模型和齿背碰撞模型。根据齿轮副接触状态及受力环境, 对局部破损下多状态啮合-碰撞行为进行分类, 建立局部破损下渐开线直齿轮系统啮合-碰撞离散动力学模型, 探讨局部破损对齿轮系统啮合刚度和载荷分配的影响特征。分析局部破损下接触力变化机理, 定义Poincaré映射截面, 研究载荷系数和啮合频率变化下系统混沌、分岔特性。研究发现, 局部破损影响接触力单双齿啮合区域, 降低齿轮局部承载能力; 较大载荷抑制齿背碰撞, 较小载荷诱发周期运动共存现象和齿背碰撞; 较大和较小啮合频率诱发齿背碰撞; 混沌运动和周期运动共存现象诱发齿背碰撞, 局部破损影响多周期共存现象, 加剧系统运动的复杂性。揭示主动轮局部破损下考虑能量耗散的齿轮系统动力学模型及非线性振动机理, 探究齿背碰撞发生条件。研究成果为故障齿轮系统非线性动力学建模和分析提供了新的方法和思路。
Key words: gear system / localized tooth breakage / back-side impact / multi-state meshing / nonlinear dynamics
关键字 : 齿轮系统 / 局部破损 / 齿背碰撞 / 多状态啮合 / 非线性动力学
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
齿轮能够高效地传递动力和运动, 被广泛应用于各种机械装备。轮齿轻微局部破损带病运行的现象普遍存在, 且影响齿轮系统的平稳性和寿命。齿轮系统在高速、轻载等工况下出现拍击现象, 研究局部破损下直齿轮系统啮合-碰撞特性, 对提高齿轮系统传动性能和健康、稳定运行具有重要意义。
针对齿轮故障, 目前大多数学者主要关注裂纹和磨损等对齿轮系统的影响, Thirumurugan等[1–2]用有限元法研究了载荷对齿轮裂纹扩展路径的影响; 刘杰等[3]建立了太阳轮裂纹故障下行星齿轮系统动力学模型; 周亚田等[4]基于Hertz接触理论和Archard公式建立齿轮系统磨损模型; 马锐等[5]考虑轮齿折断, 建立了齿轮系统动力学模型; Yang等[6]建立了齿尖崩坏下齿轮时变啮合刚度模型。Park[7]建立了一种改进的齿尖崩裂故障下直齿轮系统模型。但上述模型没有考虑多状态啮合及局部破损故障对齿轮系统动力学特征的影响。齿侧间隙诱发齿轮脱啮、齿背接触等多状态啮合行为[8]; 尹桩等[9]建立了考虑齿面冲击和摩擦的齿轮系统动力学模型; Shi等[10–11]建立了考虑时变间隙的齿轮系统多状态啮合模型。Huang等[12]建立了非对称齿轮系统动力学模型。高建设等[13]讨论了齿轮-轴承系统中擦边碰撞对系统动力学性能的影响。金花等[14]分析了多吸引子共存下齿轮系统共存吸引子的演化规律。但这些研究大多针对正常或健康齿轮, 忽略局部破损下的动态特征和齿背接触的瞬时性。
本文引入Hu等[15]建立的连续接触力模型, 定义齿背接触为齿背碰撞。针对主动轮一个轮齿局部破损故障, 讨论局部重合度的变化, 对局部破损下齿轮系统多状态啮合-碰撞行为进行分类; 建立局部破损下单级齿轮系统动力学模型; 讨论局部破损对时变因子和接触力的影响; 定义2种Poincaré映射截面, 利用变步长的四阶Runge-Kutta法求解齿轮系统动力学模型, 结合系统分岔图、碰撞力周期图、相图、Poincaré截面图等, 研究局部破损下直齿轮系统随载荷和啮合频率变化的啮合-碰撞特性, 并与健康齿轮系统随载荷变化的运动迁移过程进行对比。得到的结果为齿轮系统参数设计和局部破损故障预测提供理论参考。
1 局部破损下直齿轮系统动力学建模
假设齿轮副为刚性支撑, 仅考虑齿背碰撞, 其简化的啮合-碰撞物理模型如图 1所示。
该模型中, cg为啮合阻尼, 为齿侧间隙一半, μ为摩擦因数, e(t)=Eaωhcos(ωht)为动态传递误差, Ea为误差波动系数, ωh为啮合频率, km(t)为时变啮合刚度, R为碰撞恢复系数, Tj, θj, Ii和Rbj分别为转矩、转动角位移、转动惯量和基圆半径(j=p, g分别代表主、从动轮, 相关几何参数见表 1)。
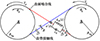 |
图1 齿轮系统啮合-碰撞物理模型 |
齿轮几何参数
1.1 局部破损齿轮副啮合表征与时变重合度计算
图 2为齿轮啮合线细节图, AD为正常齿轮副实际啮合线, AB或CD为双齿啮合区, BC为单齿啮合区。局部破损轮齿在D1点提前退出啮合, BB1或DD1由原来的双齿啮合区变为单齿啮合区, 即AB1或CD1为双齿啮合区, B1C为单齿啮合区。εm为健康齿轮副重合度, εb为局部破损下齿轮副重合度, 1 < εb < εm < 2, 经推导εb由(1)式得到。
式中:pb为基圆齿距;lAD1为啮合线AD1的长度, 可由(2)式计算得到。
式中:Rab和αab分别为破损轮齿齿顶圆半径和压力角;Rag为从动轮齿顶圆半径。
 |
图2 啮合线细节示意图 |
1.2 局部破损齿轮多状态啮合-碰撞行为分类
令轮齿相对位移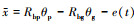 , 运动时间
, 运动时间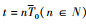 , 啮合周期
, 啮合周期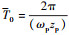 , 假设局部破损影响第nb个啮合周期, 其余第nf周期均为健康啮合周期, S={ nb mod(n, zp)=1}, P={nf}, S∪P=N, 根据
, 假设局部破损影响第nb个啮合周期, 其余第nf周期均为健康啮合周期, S={ nb mod(n, zp)=1}, P={nf}, S∪P=N, 根据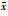 与
与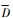 的关系, 齿轮副啮合-碰撞行为分为以下5种类型。
的关系, 齿轮副啮合-碰撞行为分为以下5种类型。
1) 双齿齿面啮合, 边界条件为
 , 当啮合点在区域AB1或CD1时, εs=εb, n=nb, 为破损双齿齿面啮合; 当啮合点在区域AB或CD时, εs=εm, n=nf, 为健康双齿齿面啮合;
, 当啮合点在区域AB1或CD1时, εs=εb, n=nb, 为破损双齿齿面啮合; 当啮合点在区域AB或CD时, εs=εm, n=nf, 为健康双齿齿面啮合;
2) 单齿齿面啮合Ⅰ(区域BC), 边界条件为
3) 单齿齿面啮合Ⅱ, 局部破损引起双齿啮合区变为单齿啮合区(区域B1B或D1D), 边界条件为
4) 轮齿脱啮(区域AD), 边界条件为
5) 齿背碰撞(理论上在区域AD任意位置), 边界条件为: 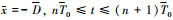 。
。
1.3 啮合-碰撞动力学建模
1) 双齿齿面啮合
图 3为双齿齿面啮合受力分析图, 该状态2个轮齿对同时啮合, 对应图 2中的AB和CD或AB1和CD1区域。根据牛顿第二定律, 主、从动轮绝对转动方程如(3)式所示, 针对健康和破损齿轮副, 其边界条件不同, 分别用εm和εb来表征。
式中: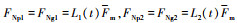 ;总动态啮合力
;总动态啮合力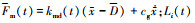 为第i(i=1, 2)对啮合轮齿的载荷分配系数;kmd(t)为双齿齿面啮合刚度。第i对啮合轮齿主、从动轮所受的摩擦力Ffpi, Ffgi见(4)式。
为第i(i=1, 2)对啮合轮齿的载荷分配系数;kmd(t)为双齿齿面啮合刚度。第i对啮合轮齿主、从动轮所受的摩擦力Ffpi, Ffgi见(4)式。
式中, μdi和λdi(t)分别为第i(i=1, 2)对啮合轮齿的干摩擦因数和摩擦力方向系数。
(3) 式中, Sdpi(t), Sdgi(t)为第i(i=1, 2)对啮合轮齿的主、从动轮摩擦力臂, 可由(5)式计算得到, 且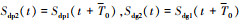 。
。
考虑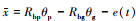 , (3)式可化简为
, (3)式可化简为
式中:me为等效质量; gdi(t)为第i(i=1, 2)对啮合轮齿对的等效摩擦力臂;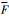 为总负载;
为总负载;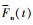 为齿轮副内部误差激励,且有
为齿轮副内部误差激励,且有
2) 单齿齿面啮合Ⅰ
单齿齿面啮合Ⅰ为健康单齿啮合, 仅一对轮齿参与啮合, 对应图 2中BC区域, 动力学方程为
式中, kms(t)为单齿齿面啮合刚度, 单齿齿面啮合Ⅰ对应的刚度为kms1(t)。
3) 单齿齿面啮合Ⅱ
图 4为单齿齿面啮合Ⅱ受力分析图, 主动轮轮齿局部破损导致同时啮合轮齿对减少, 对应图 2齿面啮合线B1B或D1D区域。其动力学方程同(7)式, 差异性表现为边界条件及kms(t), 单齿齿面啮合Ⅱ刚度为kms2(t), 详细计算见第2.1节。
4) 轮齿脱啮
轮齿脱啮时两齿轮相互分离, 齿面法向啮合力和齿面摩擦力均为零, 其运动方程如下
5) 齿背碰撞
令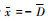 时, 发生齿背接触, 其碰撞方程为
时, 发生齿背接触, 其碰撞方程为
式中: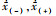 为碰撞前、后的相对速度, 根据文献[15], 最大碰撞力Fc可由(10)式计算得到。
为碰撞前、后的相对速度, 根据文献[15], 最大碰撞力Fc可由(10)式计算得到。
式中: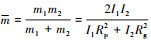 为等效质量;kc(t)为时变齿背接触刚度;Rp和Rg分别为主、从动轮分度圆半径。
为等效质量;kc(t)为时变齿背接触刚度;Rp和Rg分别为主、从动轮分度圆半径。
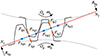 |
图3 双齿齿面啮合受力分析示意图 |
 |
图4 单齿齿面啮合Ⅱ受力分析示意图 |
1.4 归一化处理
根据齿面啮合条件, 引入啮合力函数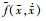 和啮合状态函数
和啮合状态函数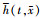 , 齿面啮合动力学方程为
, 齿面啮合动力学方程为
式中,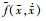 和
和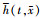 见(12)~(13)式。
见(12)~(13)式。
式中: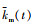 为综合时变啮合刚度;cg为系统阻尼。
为综合时变啮合刚度;cg为系统阻尼。
式中: 和
和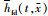 为正常单、双齿齿面啮合状态方程;
为正常单、双齿齿面啮合状态方程;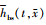 和
和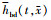 为破损单、双齿齿面啮合状态方程。正常和破损单、双齿啮合状态函数仅为边界条件的差异, 形式上相同。单、双齿齿面啮合状态方程见(14)~(15)式。
为破损单、双齿齿面啮合状态方程。正常和破损单、双齿啮合状态函数仅为边界条件的差异, 形式上相同。单、双齿齿面啮合状态方程见(14)~(15)式。
系统固有频率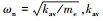 为平均啮合刚度, 无量纲时间τ=ωnt, 无量纲啮合频率ω=ωn/ωh, ωh为啮合频率。引入特征尺寸Dc, 系统无量纲参数如下:
为平均啮合刚度, 无量纲时间τ=ωnt, 无量纲啮合频率ω=ωn/ωh, ωh为啮合频率。引入特征尺寸Dc, 系统无量纲参数如下: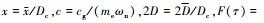
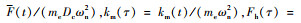
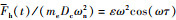 , 则(13)式可无量纲化为
, 则(13)式可无量纲化为
式中: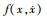 为无量纲动态啮合力函数;h(τ, x)为无量纲状态函数, 见(17)~(18)式。
为无量纲动态啮合力函数;h(τ, x)为无量纲状态函数, 见(17)~(18)式。
式中:T0为无量纲啮合周期;hfs(τ, x), hfd(τ, x)为健康单、双齿齿面啮合无量纲状态方程; hbs(τ, x), hbd(τ, x)为破损下单、双齿齿面啮合无量纲状态方程, 详细计算见(19)~(20)式。
综上, 局部破损下直齿轮系统啮合-碰撞非线性动力学模型无量纲归一化方程可表示为
式中: 分别表示齿背碰撞前、后的无量纲相对速度, 无量纲综合动态接触力见(22)式。
分别表示齿背碰撞前、后的无量纲相对速度, 无量纲综合动态接触力见(22)式。
2 时变参数计算
根据文献[6, 12]等的研究, 该模型主要研究局部破损对时变接触刚度和时变载荷分配系数的影响, 将啮合阻尼和齿侧间隙等效为恒定参数, 研究局部破损下齿轮系统非线性啮合-碰撞动态特性。
2.1 时变刚度计算
假设无量纲齿面啮合刚度km(τ)和齿背接触刚度kc(τ)相等, 由(23)式计算得到。
式中:kh为时变赫兹接触刚度[3], 弯曲刚度kbji, 轴向压缩刚度kaji, 剪切刚度ksji, 基体刚度kf(j=p, g分别表示主、从动轮, i=1, 2分别表示单、双齿齿轮副接触)详细计算见文献[10–12]。
局部破损下齿面啮合时变刚度如图 5所示。km为综合时变啮合刚度(双齿齿面啮合、单齿齿面啮合Ⅰ、Ⅱ的刚度分别为kmd, kms1, kms2), km1和km2为双齿啮合第1, 2轮齿对啮合刚度。阴影部分为齿轮局部破损受到影响的啮合周期, 与健康啮合周期相比, 轮齿局部缺失, 部分双齿啮合变为单齿啮合, 双齿啮合区减小, 单齿啮合区增大, 对应时变啮合刚度减小, 轮齿局部承载能力减弱。
 |
图5 局部破损下时变啮合刚度 |
2.2 时变载荷分配系数计算
根据文献[12]的研究, 局部破损下齿面啮合载荷分配系数L(ξ)可由(24)式计算得到。
式中:ξA和ξD分别表示啮合点A和D的齿廓参数;ξD1为点D1的齿廓参数;ξC(t)为AD上任意啮合点的齿廓参数, 见(25)式。
图 6为局部破损下时变载荷分配系数。Li为第i对啮合轮齿的载荷分配系数(i=1, 2), 同正常周期相比, 破损周期中双齿啮合区部分变为单齿啮合区(单齿啮合Ⅱ区), 导致双齿啮合区减小, 单齿啮合区增大, 载荷作用在一对轮齿上。可见, 轮齿局部破损使其邻近轮齿局部过载, 加剧疲劳。
 |
图6 局部破损下时变载荷分配系数 |
3 啮合-碰撞非线性动力学特性研究
为分析局部破损下齿轮系统多状态啮合-碰撞行为机理, 定义2种不同的Poincaré映射截面, 频闪映射截面βn和齿背接触映射截面βc。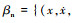
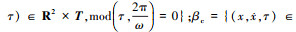
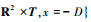 。
。
结合相图、Poincaré截面图、动态接触力、时间历程图等分析齿轮系统啮合-碰撞特性。通过相图(x≥D, 系统为齿面啮合; -D < x < D, 系统为轮齿脱啮; x=-D, 系统为齿背碰撞)和Poincaré截面图辨识齿轮系统多状态啮合-碰撞行为及运动周期; 结合齿轮系统多初值分岔图与Fc周期图, 讨论系统随啮合频率和载荷变化的啮合-碰撞特性。
3.1 局部破损下接触力变化规律
取系统参数: c=0.01, μd1=μd2=0.15, ε=0.05, F=0.05, D=1.0, ω=1.1, R=0.85。图 7a)为局部破损下Fm时间历程图, Fm>0, Fm=0和Fm < 0呈周期变化规律, 系统为齿面啮合-轮齿脱啮-齿背碰撞交替, 齿面啮合转迁为轮齿脱啮时(区域B), Fm>0突变为Fm < 0又突变为Fm=0;图 7b)为图 7a)区域A局部放大图, T1和T2为健康单、双齿齿面啮合周期, Tb1, Tb2为局部破损下齿轮单、双齿啮合周期, 可以看出Tb1>T1, Tb2 < T1, T1+T2=Tb1+Tb2=T0, 破损轮齿使得单齿啮合周期增大, 双齿啮合周期减小, 且变化量相同, Tb1-T1=T2-Tb2=(εm-εb)T0。局部破损使得部分区域Fm减小, 动力传输能力降低。
 |
图7 动态接触力时间历程图 |
3.2 载荷系数的影响
其他参数不变, ω=1.2, F∈(0, 0.15]作为参数变量, 图 8为局部破损下齿轮系统随F递减的多初值分岔图和Fc周期变化图, 图 8a)为βn截面的分岔图; 图 8b)为βc截面的Fc周期图。F较大, 系统为周期1运动, 其相图和Poincaré截面图见图 9a), 齿面啮合-轮齿脱啮交替; 随F减小, 在A点周期1运动一部分初值下突变为混沌后立即退化为周期4运动, 另一部分初值下转迁为周期2运动, 导致周期2和周期4运动共存, 其相图和Poincaré截面图见图 9b), 周期4运动的拓扑结构远大于周期2运动, 意味着周期4运动的振动强于周期2;在B点周期2运动在部分初值下激变为混沌运动, 周期4运动保存不变, 导致周期4和混沌运动共存; 在C点周期4运动退化为周期2运动, 导致周期2和混沌运动共存, 其相轨迹和Poincaré截面图如图 9c)所示; 在D点混沌运动在一部分初值下退化为周期6运动, 另一部分初值下仍保持周期2运动, 导致周期2和周期6运动共存, 其相图和Poincaré截面图如图 9d)所示, 周期2运动的拓扑结构大于周期6, 意味着周期2运动的振动强于周期6;在E点, 周期6运动退化为周期3运动, F点周期2运动消失, 周期共存现象消失, 导致周期2和周期3运动共存; 周期3运动经G点跳跃转迁为周期6运动, 后在H点突变为长周期或非周期运动。
综上所述, F较大时, 系统为稳定的周期运动且无齿背碰撞, 随F减小, 出现混沌运动及周期共存现象以及齿背碰撞行为, F较小时, 齿背碰撞依然存在, 但周期共存现象消失。较大载荷抑制齿背碰撞, 较小载荷、混沌运动和多周期共存现象诱发齿背碰撞。在齿轮系统参数设计、优化时, 诱发齿背碰撞的载荷范围应尽可能避免, 实际工作中可以调节初值来改善齿轮运动状态。
 |
图8 局部破损下齿轮系统随载荷变化的多初值分岔图和碰撞力周期变化图 |
 |
图9 不同载荷系数对应的相图和Poincaré截面图 |
3.3 啮合频率的影响
令F=0.11, ω∈[0.1, 2.5], 局部破损下齿轮系统随ω递增的多初值分岔图和Fc周期变化图如图 10所示。图 10a)为βn截面的分岔图; 图 10b)为βc截面的Fc周期图。随着ω的增大, 混沌运动在I点退化为周期1运动, 齿背碰撞消失, 混沌运动的相轨迹如图 11a)所示。在J点周期1在一部分初值下转迁为周期2运动, 在另一部分初值下持续存在, 导致周期1与周期2的共存, 相轨迹和Poincaré截面图见图 11b), 周期2运动为齿面啮合-轮齿脱啮交替, 周期1运动仅表现为齿面啮合, 周期2运动的振动明显强于周期1。在K点一部分初值下由周期1运动跳跃为周期3运动, 另一部分初值下仍表现为周期2运动, 导致周期2和周期3运动共存。在L点一部分初值下由周期3运动转迁为周期8运动, 另一部分初值下仍表现为周期2运动, 导致周期2和周期8运动共存, 相轨迹和Poincaré截面图见图 11c), 两种周期运动均为齿面啮合-轮齿脱啮交替, 周期8运动的振动明显强于周期2。在M点周期8运动消失, 系统均表现为周期2运动, 后在N点周期2在一部分初值下经边界激变进入混沌, 并出现齿背碰撞, 另一部分初值下仍保持周期2运动并进行一系列演化: 在N和O之间, 混沌和周期2运动共存; P和Q之间, 混沌和周期1运动共存; Q和R之间, 混沌和周期4运动共存; A和T之间, 混沌和周期3运动共存。在T点, 混沌运动消失, 系统退化为周期3运动, 相轨迹和Poincaré截面图见图 11d), 齿面啮合-轮齿脱啮-齿背碰撞交替。
由上可见, 当ω较小时, 系统为混沌运动, Fc随ω增大而减小, 且混沌运动退化为周期运动, 齿背碰撞消失, 系统经过一系列演化, 再次激变为混沌运动, 齿背碰撞行为和共存现象再次出现; ω较大时, 系统表现为齿面啮合-轮齿脱啮-齿背碰撞交替行为。齿轮系统在ω较大或较小时均出现混沌, 并诱发齿背碰撞行为。避免系统在ω较大或较小的区间运行, 能够一定程度避免齿背碰撞, 保证齿轮系统的健康、平稳运行。
 |
图10 局部破损下齿轮系统随啮合频率变化的多初值分岔图和碰撞力周期变化图 |
 |
图11 不同啮合频率对应的相图和Poincaré截面图 |
3.4 局部破损与健康齿轮系统对比
系统参数同3.2节, 健康齿轮系统随载荷系数递减的多初值分岔图见图 12。图 12a)为βn截面对应的分岔图; 图 12b)为βc截面对应的Fc周期图。在A′点右侧, 系统为周期2和周期1运动共存, 且无齿背碰撞行为, 周期1运动在A′点激变为混沌运动, 后在B′点退化为周期6运动, 并在C′点再次进入混沌, 周期2运动在B′点突变为混沌运动。在A′和B′之间, 混沌和周期2运动共存; B′和C′之间, 混沌和周期6运动共存; 在D′点, 混沌运动退化为周期6运动, 并在E′点突变为周期3运动, 后经F′点跳跃转迁为周期6运动。
对比图 8和图 12发现: 样本参数下, 轮齿局部破损影响齿轮系统混沌、分岔特性和周期运动共存现象。F较大时, 局部破损影响齿轮系统周期运动共存, 但仍抑制齿背碰撞行为; 随着F减小, 局部破损影响下, 系统提前出现齿背碰撞并出现周期共存, 加剧系统动力学行为的复杂程度; 较小载荷下, 局部破损对系统的影响逐渐较小, 但可能出现长周期运动, 影响系统稳定性, 加剧系统振动。
 |
图12 健康齿轮系统随载荷系数变化的多初值分岔图和碰撞力周期变化图 |
4 结论
本文建立了主动轮局部破损下直齿轮系统啮合-碰撞动力学模型, 研究了齿轮系统分岔、混沌和啮合-碰撞特性, 具体结论如下:
1) 局部破损轮齿提前退出啮合, 影响齿轮副重合度和单、双齿啮合区域(双齿啮合区减小, 单齿啮合区增大), 引起了齿轮系统接触刚度、载荷分配和动态接触力变化, 降低邻近轮齿局部承载力。
2) 引入碰撞恢复系数, 建立考虑能量耗散的局部破损齿轮系统啮合-碰撞模型, 该模型一定程度上反映了齿轮传动实际过程, 为齿轮系统参数设计、优化及局部破损故障检测与维护提供参考, 为齿轮系统动力学建模和分析提供新的方法和思路。
3) 随啮合频率和载荷系数的变化, 系统动力学响应发生演化: 啮合频率较大或较小时, 系统出现混沌或齿背碰撞, 系统运动性能较差; 较大载荷下, 系统运动较为稳定且无齿背碰撞行为。混沌和周期运动共存均诱发齿背碰撞, 加剧系统运动的复杂性, 实际工作中可通过调节初值来改善系统运动状态, 进而提高齿轮传动的平稳性。
4) 对比局部破损和健康齿轮系统, 不同载荷条件下, 局部破损对系统运动状态产生不同程度影响。较小载荷下, 局部破损可能引发高周期运动; 随载荷增大, 局部破损诱发周期运动共存现象, 加剧系统运动复杂性, 并诱发齿背碰撞; 较大载荷下, 局部破损影响周期运动共存, 但仍抑制齿背碰撞。为保证齿轮在较大载荷下运行, 可通过调整初值改善齿轮系统的动态特性, 能够一定程度降低局部破损对齿轮系统造成的不利影响。
References
- THIRUMURUGAN R, GNANASEKAR N. Influence of finite element model, load-sharing and load distribution on crack propagation path in spur gear drive[J]. Engineering Failure Analysis, 2020, 110: 104383. [Article] [CrossRef] [Google Scholar]
- THIRUMURUGAN R. Study on the quality and tooth root load carrying capacity of the high contact ratio asymmetrical gear tooth machined using WCEDM process[J]. Materials and Manufacturing Processes, 2020, 35(12): 1352–1361. [Article] [CrossRef] [Google Scholar]
- LIU Jie, ZHANG Lei, ZHAO Siyu, et al. Dynamic characteristic of wind turbine planetary set with crack in sun gear[J]. Acta Energiae Solaris Sinica, 2019, 40(1): 192–198. [Article] (in Chinese) [Google Scholar]
- ZHOU Yatian, ZHANG Ruiliang, WANG Tie, et al. Influence of tooth surface wear on contact load of spur gears[J]. Machinery Design & Manufacture, 2021, 365(7): 58–61. [Article] (in Chinese) [Google Scholar]
- MA Rui, WANG Hui. Dynamics analysis of the gear system with tooth breakage fault[J]. Journal of Mechanical Transmission, 2017, 41(3): 147–150. [Article] (in Chinese) [Google Scholar]
- YANG S, HU N, TANG J, et al. Dynamic analysis for a spur geared rotor system with tooth tip chipping based on an improved time-varying mesh stiffness model[J]. Mechanism and Machine Theory, 2021, 165: 104435. [Article] [CrossRef] [Google Scholar]
- PARK C I. Dynamic behavior of the spur gear system with time varying stiffness by gear positions in the backlash[J]. Journal of Mechanical Science and Technology, 2020, 34(2): 565–572. [Article] [CrossRef] [Google Scholar]
- SHI Jianfei, GOU Xiangfeng, ZHU Lingyun. Dynamic modeling and analysis of involute spur gear transmission system considering friction and multi-state meshing conditions[J]. Journal of Northwestern Polytechnical University, 2020, 38(2): 401–411. [Article] (in Chinese) [CrossRef] [EDP Sciences] [Google Scholar]
- YIN Zhuang, GOU Xiangfeng, ZHU Lingyun, et al. Dynamic modeling and analysis of single-stage gear system considering tooth surface impact and friction[J]. Journal of Vibration Engineering, 2018, 31(6): 974–983. [Article] (in Chinese) [Google Scholar]
- SHI J, GOU X, ZHU L. Modeling and analysis of a spur gear pair considering multi-state mesh with time-varying parameters and backlash[J]. Mechanism and Machine Theory, 2019, 134: 582–603. [Article] [CrossRef] [Google Scholar]
- SHI J, GOU X, ZHU L. Generation mechanism and evolution of five-state meshing behavior of a spur gear system considering gear-tooth time-varying contact characteristics[J]. Nonlinear Dynamics, 2021, 106(3): 2035–2060. [Article] [CrossRef] [Google Scholar]
- HUANG Q, TANG W, LU R, et al. Influence of system-inherent phase in spur gear multi-state mesh based on nonlinear dynamics[J]. Mechanical Systems and Signal Processing, 2022, 172: 108749. [Article] [CrossRef] [Google Scholar]
- GAO Jianshe, CUI Bingqi, DING Shunliang. Dynamic characteristics analysis of grazing impact of gear-bearing transmission system[J]. Journal of Vibration and Shock, 2022, 41(13): 1–7. [Article] (in Chinese) [Google Scholar]
- JIN Hua, LYU Xiaohong, ZHANG Zihao, et al. Discontinuous bifurcations of coexisting attractors for a gear transmission system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(1): 203–212. [Article] (in Chinese) [Google Scholar]
- HU S, GUO X. A dissipative contact force model for impact analysis in multibody dynamics[J]. Multibody System Dynamics, 2015, 35(2): 131–151. [Article] [Google Scholar]
All Tables
All Figures
 |
图1 齿轮系统啮合-碰撞物理模型 |
| In the text | |
 |
图2 啮合线细节示意图 |
| In the text | |
 |
图3 双齿齿面啮合受力分析示意图 |
| In the text | |
 |
图4 单齿齿面啮合Ⅱ受力分析示意图 |
| In the text | |
 |
图5 局部破损下时变啮合刚度 |
| In the text | |
 |
图6 局部破损下时变载荷分配系数 |
| In the text | |
 |
图7 动态接触力时间历程图 |
| In the text | |
 |
图8 局部破损下齿轮系统随载荷变化的多初值分岔图和碰撞力周期变化图 |
| In the text | |
 |
图9 不同载荷系数对应的相图和Poincaré截面图 |
| In the text | |
 |
图10 局部破损下齿轮系统随啮合频率变化的多初值分岔图和碰撞力周期变化图 |
| In the text | |
 |
图11 不同啮合频率对应的相图和Poincaré截面图 |
| In the text | |
 |
图12 健康齿轮系统随载荷系数变化的多初值分岔图和碰撞力周期变化图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


