Studies on meshing clearance of thread pairs of planetary roller screw mechanism in different directions

Wei CAI; Xiaojun FU; Shangjun MA; Xin LI; Geng LIU

doi:10.1051/jnwpu/20244230540

All issues

Volume 42 / No 3 (June 2024)

JNWPU, 42 3 (2024) 540-549

Full HTML

Open Access

Issue		JNWPU Volume 42, Number 3, June 2024


Page(s)		540 - 549
DOI		https://doi.org/10.1051/jnwpu/20244230540
Published online		01 October 2024

JNWPU 2024, 42(3): 540–549

Studies on meshing clearance of thread pairs of planetary roller screw mechanism in different directions

不同方向上行星滚柱丝杠螺纹副啮合侧隙研究

Wei CAI (蔡威), Xiaojun FU (付晓军), Shangjun MA (马尚君), Xin LI (李欣) and Geng LIU (刘更)

Shaanxi Engineering Laboratory for Transmissions and Controls, Northwestern Polytechnical University, Xi'an 710072, China

Received: 16 May 2023

Abstract

The helix surface model of planetary roller screw mechanism (PRSM) is established by utilizing the parametric equations of space surface according to the structural features of screw, roller and nut. The helix surface model of PRSM is improved in consideration of the PRSM assembly relationship. The normal vector equations of helix surfaces are obtained based on the helix surface model. The meshing clearance models of PRSM in axial, radial and circumferential directions are built considering the movement direction of parts utilizing surface meshing conditions. The influence of structural parameters on the meshing clearance of PRSM is also analyzed. The results show that the meshing points between the roller and the screw in three directions are not in the middle diameter. The meshing points in the three directions of the roller and the nut are in the middle diameter of the roller. The pitch, tooth angle and tooth thickness of the thread all have an influence on the meshing clearance of PRSM. Only by increasing the tooth thickness of the thread can the meshing clearance in the three directions be reduced at the same time. The pitch and tooth angle should be selected properly to meet the practical requirements.

摘要

根据丝杠、滚柱以及螺母结构特征, 利用空间曲面参数方程分别建立了行星滚柱丝杠各个零件的螺旋曲面模型, 并结合行星滚柱丝杠装配关系, 得到行星滚柱丝杠空间啮合曲面方程。在此基础上, 获得螺旋曲面法向量, 基于曲面啮合条件, 考虑零件运动方向, 建立了行星滚柱丝杠在轴向、径向以及周向上的啮合侧隙模型, 并讨论了结构参数对行星滚柱丝杠啮合侧隙的影响规律。结果表明, 滚柱与丝杠侧在3个方向上的啮合点均不在螺纹中径, 滚柱与螺母侧3个方向上的啮合点均在滚柱螺纹中径位置; 螺距、牙侧角以及螺纹牙厚均对行星滚柱丝杠啮合侧隙有影响, 只有增大螺纹牙厚才能同时减小3个方向上的啮合侧隙, 螺距和牙侧角应根据实际需要选择合适的参数。

Key words: planetary roller screw mechanism / thread pairs / different directions / meshing clearance /

关键字 : 行星滚柱丝杠 / 螺纹副 / 曲面方程 / 不同方向 / 啮合侧隙

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

行星滚柱丝杠(planetary roller screw mechani-sm, PRSM)是一种利用螺纹结构将旋转运动转化成直线运动的螺旋传动机构[1]。PRSM内部含有多个滚柱, 呈现多个螺纹牙同时啮合, 具有大推力、高精度、长寿命以及高可靠性等优势[2–3], 逐渐应用在航空航天[4]、机器人[5]、医疗器械[6]和精密机床[7]等领域。

国内外针对PRSM的研究主要是在载荷分布[8–9]、摩擦效率[10–11]、热特性[12]、运动学[13–14]以及故障诊断[15]等方面。现有研究表明, PRSM啮合点位置对其承载性能、运动特性均有较大影响。不同螺纹牙型参数导致其啮合点位置以及啮合侧隙发生变化, 使滚柱在丝杠、螺母内部浮动区域发生变化, 进而影响到PRSM承载能力、传动精度以及寿命等性能。

在PRSM啮合特性方面, 赵英等[16]在螺纹重叠区域划分网格, 分别针对丝杠、滚柱、螺母计算其网格节点上轴向坐标差值, 差值最小即为轴向间隙, 差值最小处节点即为啮合点。Jones等[17]基于Frenet坐标系建立PRSM啮合模型, 利用螺纹中径处螺旋升角代替啮合点处螺旋升角, 推导得到PRSM啮合点位置。付晓军等[18]根据曲面连续相切原理, 建立PRSM轴向啮合方程, 得到轴向啮合点以及侧隙。Sandu等[19]针对不同形状的螺纹截面建立了螺旋曲面方程, 计算得到不同螺纹截面轮廓下的啮合点位置。陈士云等[20]将PRSM螺旋曲面进行离散处理, 通过计算离散点在轴向上的坐标差, 可得到PRSM轴向侧隙。刘靖楠等[21]考虑了PRSM在加工以及装配过程中可能产生的各种误差, 基于刚体欧拉定理, 建立了一种考虑误差的PRSM啮合模型。上述文献计算了PRSM啮合点位置以及侧隙, 但其计算分析过程仅仅考虑轴向啮合特性, 未能深入研究径向以及周向啮合特性。不同方向上啮合点位置均会对PRSM工作性能产生影响, 尤其是不同装配条件以及工况条件会导致PRSM沿着不同方向接触, 从而影响PRSM运行效率、工作寿命等。因此, 需要充分考虑PRSM实际工作状态, 深入探究PRSM在不同方向下啮合特性以及啮合侧隙影响规律。

本文推导了PRSM螺纹曲面方程, 利用空间曲面啮合原理, 建立了PRSM在轴向、径向、周向上啮合侧隙模型, 计算了3个方向上的啮合点位置, 并探究结构参数对PRSM啮合侧隙的影响规律。

1 PRSM结构

PRSM主要有标准式、反向式、循环式、轴承环式以及差动式等多种结构形式, 其中最为常用的是标准式PRSM, 结构形式如图 1所示。标准式PRSM主要由丝杠、滚柱、螺母、内齿圈、保持架、弹性挡圈等组成。丝杠和螺母分别采用相同头数的外梯形螺纹和内梯形螺纹结构, 滚柱则采用单头圆弧牙型轮廓外螺纹结构, 并且三者螺距相等, 旋向相同。此外, 滚柱两侧端部采用轮齿结构, 从而实现螺纹副和齿轮副同时啮合。

在PRSM运动过程中, 丝杠做旋转运动, 通过滚柱与丝杠、滚柱与螺母之间螺纹啮合将其转化成螺母的直线运动。在螺纹传动过程中, 多个滚柱在保持架的作用下均匀分布在螺母与丝杠之间。滚柱在与丝杠、螺母啮合的同时, 通过端部轮齿与安装在螺母内部的内齿圈啮合, 从而实现其绕着丝杠中心轴公转, 又绕着自身旋转中心做自转运动, 进一步实现了与螺母之间无相对轴向位移。为了防止保持架脱落, 弹性挡圈被放置在螺母端部内齿圈内部凹槽中。

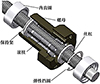图1

PRSM结构组成

2 PRSM螺纹曲面方程

本文以右旋螺纹结构的PRSM为例, 推导其丝杠与滚柱、螺母与滚柱之间的啮合侧隙, 该过程同样适用于其他旋向PRSM啮合侧隙求解问题。

丝杠、滚柱、螺母上螺纹结构均是螺纹牙轮廓绕着空间螺旋曲线旋转形成的三维空间曲面, 如图 2所示。其中O_i-x_iy_iz_i表示零件坐标系, O′_i-u_iv_iw_i表示螺纹牙轮廓坐标系, 下标i=s, r, n分别代表丝杠、滚柱以及螺母, θ_i⁰表示螺纹起点位置与x_i轴的夹角, λ_i表示对应零件螺纹齿根处螺旋升角。

丝杠、滚柱、螺母螺纹截面如图 3所示, 图中a_i表示对应零件螺纹小径到中径之间的距离; b_i表示对应零件螺纹牙厚; β_i表示对应零件螺纹牙侧角; θ_i⁰表示对应零件螺纹初始点与零件坐标系x_i轴夹角; r_i^m表示对应零件名义半径; h_i表示对应零件螺纹全齿高; r_tr表示滚柱螺纹曲面曲率半径为

因此, 在截面坐标系中, 丝杠、滚柱、螺母各自螺纹牙轮廓曲线坐标方程为

(2)~(4)式中, ζ_s, ζ_r, ζ_n分别表示丝杠、滚柱以及螺母螺纹牙上、下曲线, 取值为1时, 表示上曲线，取值为-1时, 表示下曲线。

根据空间坐标转换关系, 可将螺纹截面坐标系向零件坐标系变换, 其转换关系为

式中, H为变换矩阵，具体可表示为[21]

式中, r_i^f表示对应零件螺纹齿根圆半径，有

由(2)~(7)式可得, 在零件坐标系中, 丝杠、滚柱以及螺母螺纹牙轮廓曲面方程为[18]

PRSM在全局坐标系O-xyz中位置关系如图 4所示, 其中, m_r, m_s, m_n分别表示滚柱、丝杠以及螺母螺纹起点, 螺母、丝杠零件坐标系应与全局坐标系重合, 滚柱零件坐标系应与全局坐标系平行。

根据PRSM装配关系, 丝杠螺纹起点与螺母螺纹起点相差角度为π/n_n。所以, 螺母螺纹起点初始角度为

式中, n_n表示螺母螺纹头数。

根据滚柱在运动过程中既公转又自转的运动原理, 在装配过程中, 可根据公转角度和自转角度确定滚柱螺纹起点位置, 从而实现丝杠与滚柱、螺母与滚柱装配关系。滚柱螺纹起点初始角度为

式中, n_s表示丝杠螺纹头数。

综上, 结合PRSM装配关系, 丝杠、滚柱以及螺母在全局坐标系螺旋曲面坐标方程为

(13)~(15)式中, 零件螺纹齿根处螺旋升角λ_i满足如下关系

式中：p表示螺纹螺距；n_i表示螺纹头数。

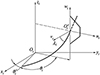图2

PRSM零件坐标系和螺纹牙轮廓坐标系

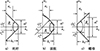图3

PRSM螺纹牙轮廓

图4

PRSM在全局坐标系位置关系

3 PRSM螺纹副啮合侧隙

PRSM螺纹副啮合间隙对其传动性能有一定的影响。因此, 基于空间曲面啮合条件, 建立PRSM螺纹副啮合侧隙模型, 精确计算螺纹副啮合侧隙能够为PRSM工程设计提供理论基础。

3.1 空间曲面啮合条件

空间曲面位置关系如图 5所示, Λ₁, Λ₂为两不重合的空间曲面, Ω₁, Ω₂分别为Λ₁, Λ₂切平面, n₁, n₂表示Λ₁, Λ₂空间曲面法向量, n₁₂表示曲面Λ₁或Λ₂移动方向, Q₁, Q₂表示两空间曲面沿着n₁₂方向移动一定距离后相切, 此时的切点位置, 即在n₁₂方向上的啮合点。

基于空间曲面之间最短距离理论, 两空间曲面之间存在距离最短的两点, 同时两点之间的连线必然与空间曲面上该点的法向量方向相同或者相反。但当空间曲面沿着任意方向移动后相切, 其最短距离方向应与移动方向相同或者相反, 可得

式中: μ, τ表示长度系数; τ=0, 表示两空间曲面相切; τ>0, 表示两空间曲面相离; τ < 0, 表示两空间曲面相交。

曲面Λ₁, Λ₂啮合点之间位移为

式中, x_Q₁, y_Q₁, z_Q₁, x_Q₂, y_Q₂, z_Q₂分别表示Q₁, Q₂点空间位置坐标。

由(18)~(20)式, 可求出空间曲面Λ₁, Λ₂在 n₁₂方向上的啮合点位置, 并且曲面沿着该方向移动最短距离为

图5

空间曲面位置关系

3.2 PRSM啮合侧隙

3.2.1 PRSM螺旋曲面法向量

通过PRSM螺旋曲面参数方程(13)~(15)式分别对r_i, θ_i求偏导, 可得螺旋曲面切向量为

利用螺旋曲面切向量, 可以得到丝杠、滚柱以及螺母在任一点处法向量为[2]

式中: ε_i为常数1或-1, 外螺纹值取1;内螺纹值取-1。

3.2.2 PRSM轴向侧隙

PRSM轴向侧隙是指装配后的PRSM在轴向上移动的最大距离。在全局坐标系中, PRSM移动方向向量为

以丝杠和滚柱为例, 轴向移动, 丝杠上螺旋曲面和滚柱下螺旋曲面接触, ζ_s, ζ_r分别为1, -1。丝杠和滚柱都是外螺纹, 所以ε_s, ε_r均为1, 并代入到(14)~(15)式及(24)式。

根据空间曲面啮合原理, 结合丝杠、滚柱空间曲面坐标方程以及法向量, 可以得到其轴向啮合点满足如下关系

通过(26)式可求解出丝杠侧啮合半径r_s1^a、啮合角θ_s1^a以及滚柱侧啮合半径r_rs1^a、啮合角θ_rs1^a。进一步, 可求得丝杠上螺旋曲面和滚柱下螺旋曲面轴向啮合侧隙为

同理将ζ_s, ζ_r分别取-1, 1, 代入到(26)式中, 可以求解得到丝杠下螺旋曲面和滚柱上螺旋曲面啮合时丝杠侧啮合半径r_s2^a，啮合角θ_s2^a以及滚柱侧啮合半径r_rs2^a，啮合角θ_rs2^a, 并得到其啮合侧隙为

因此, 丝杠与滚柱轴向啮合侧隙为

在求解螺母与滚柱啮合点时, 螺母为内螺母, ε_n为-1, 并结合(15)~(16)式, (24)~(25)式, 可得到螺母、滚柱啮合方程为

将ζ_n, ζ_r取-1, 1代入(30)式中, 得到螺母下螺旋曲面与滚柱上螺旋曲面啮合侧隙为

式中: r_n1^a, r_rn1^a分别表示螺母侧、丝杠侧啮合半径; θ_n1^a, θ_rn1^a分别表示螺母侧、丝杠侧啮合角。

ζ_n,ζ_r取1, -1代入(30)式中, 式中, 得到螺母上螺旋曲面与滚柱下螺旋曲面啮合侧隙为

式中：r_n2^a, r_rn2^a分别表示螺母侧、丝杠侧啮合半径；θ_n2^a, θ_rn2^a分别表示螺母侧、丝杠侧啮合角。

因此, 螺母与滚柱轴向啮合侧隙为

3.2.3 PRSM径向侧隙

PRSM径向侧隙是指丝杠、滚柱以及螺母沿着径向移动的最大距离。因此, 移动方向向量为

丝杠与滚柱径向啮合侧隙与轴向侧隙推导相似, 结合(13)~(14)式, (24)式及(34)式, 并将ζ_s, ζ_r为1, -1, ε_s, ε_r均为1代入, 可得径向啮合点满足如下关系

根据(13)~(14)式及(35)式可得丝杠与滚柱径向啮合侧隙为

式中: r_rs^r, r_s^r表示滚柱侧、丝杠侧啮合半径; θ_rs^r, θ_s^r表示滚柱侧、丝杠侧啮合角。

将ζ_n, ζ_r为-1, 1, ε_s, ε_r均为1代入(14)~(15)式，(24)式及(34)式, 可得径向啮合点满足如(37)式所示关系。

同理可得螺母与滚柱径向啮合侧隙为

式中: r_rn^r, r_s^r表示滚柱侧、丝杠侧啮合半径; θ_rn^r, θ_s^r表示滚柱侧、丝杠侧啮合角。

3.2.4 PRSM周向侧隙

丝杠或者螺母绕自身中心线转动一定角度后与滚柱啮合, 此时转动的角度即为PRSM周向侧隙。在计算丝杠与滚柱侧周向侧隙时, 与PRSM轴向侧隙、径向侧隙求解过程不同, 将周向侧隙δ_sr^t直接代入(13)~(14)式及(24)式, 可得

将ζ_s, ζ_r分别为1, -1, 代入到(39)式中, 可得到丝杠上螺旋曲面与滚柱下螺旋曲面啮合时周向侧隙δ_sr1^t。此外, 将ζ_s，ζ_r为-1，1同样代入到(39)式中, 可得到丝杠下螺旋曲面与滚柱上螺旋曲面啮合时周向侧隙δ_sr2^t。所以, 滚柱与丝杠周向侧隙为

同理, 可得螺母与滚柱之间的周向侧隙满足关系为

先后将ζ_n, ζ_r为1, -1以及ζ_n, ζ_r为-1, 1代入(41)式, 分别得到螺母上螺旋曲面与滚柱下螺旋曲面啮合时周向侧隙δ_nr1^t和螺母下螺旋曲面与滚柱上螺旋曲面啮合时周向侧隙δ_nr2^t。所以, 滚柱与螺母周向侧隙为

4 模型验证与讨论

4.1 模型验证

为了验证本文基于空间曲面啮合原理计算的啮合侧隙准确性, 采用文献[18]的结构参数, 如表 1所示。基于表 1结构参数，本文方法与文献[8]方法计算的侧隙对比结果如表 2所示。

表 2中文献[18]和本文计算轴向啮合点与轴向啮合侧隙均吻合, 验证了本文模型的正确性。此外, 表 2中列出了PRSM径向啮合点、啮合侧隙以及周向啮合点、啮合侧隙。

根据表 2得到丝杠与滚柱、螺母与滚柱在轴向、径向以及周向上啮合点位置关系图, 如图 6~7所示, 图中点划线表示滚柱侧、丝杠侧及螺母侧螺纹中径, 虚线和实线分别表示滚柱侧、丝杠侧及螺母侧螺纹大径和小径。图 6~7中不同形状的点分别表示滚柱与丝杠、滚柱与螺母在不同方向上的啮合点。

从图 6中可明显看出滚柱和丝杠啮合点均会偏离螺纹名义半径, 同时沿着不同方向移动或转动后啮合点位置发生一定变化。

由图 7可得滚柱与螺母啮合时, 滚柱侧3个方向上的啮合点均在滚柱螺纹中径处, 丝杠侧3个方向上的啮合点位置会发生一定变化。图 6~7说明PRSM在运动过程中其啮合点并不在一个固定位置上, 而是随着运动方向的变化而改变, 从而对PRSM运动学特性、传动效率等产生影响, 甚至导致部分螺纹牙脱啮。

PRSM结构参数

轴向啮合点位置与间隙对比结果

丝杠与滚柱侧啮合点位置

螺母与滚柱侧啮合点位置

4.2 结构参数对啮合侧隙的影响

由于不同的结构参数会改变PRSM螺纹牙轮廓, 进而对其啮合侧隙产生一定影响。下文基于本文建立的PRSM啮合侧隙模型, 探究PRSM螺距、牙侧角、螺纹牙厚等基本结构参数对啮合侧隙的影响规律。

4.2.1 螺距

不同螺距参数对PRSM轴向、径向、周向侧隙的影响规律, 如图 8~10所示。

图 8中, 丝杠侧轴向啮合侧隙先增大后减小, 螺母侧轴向啮合侧隙与螺距呈现线性关系, 并且随着螺距增大而增大。从图 9可以看出, 螺距对PRSM径向侧隙的影响规律与图 8中轴向侧隙相似, 并且对比图 8~9可以发现, 丝杠侧、螺母侧轴向侧隙均为径向侧隙的2倍。图 10中, 螺母侧周向侧隙为固定值, 说明螺距对螺母侧周向侧隙没有影响, 丝杠侧周向侧隙与螺距呈现线性关系, 随着螺距增大而减小。通过图 8~10可以看出, 减小螺距会降低轴向侧隙和径向侧隙, 但是会增大周向侧隙。因此, 在设计PRSM过程中, 应根据侧隙设计要求, 合理选择螺纹螺距。

图8

螺距对PRSM轴向侧隙影响

图9

螺距对PRSM径向侧隙影响

图10

螺距对PRSM周向侧隙影响

4.2.2 牙侧角

图 11~13为不同牙侧角对PRSM啮合侧隙的影响。图 11中, 牙侧角对螺母侧轴向间隙没有影响, 增大牙侧角会使丝杠侧周向侧隙增大。在图 12中, 丝杠侧径向侧隙与螺母侧径向侧隙呈相反趋势, 并且在牙侧角大于90°时, 丝杠侧径向侧隙几乎不再变化。图 13中, 牙侧角对螺母侧周向侧隙没有任何影响, 但会增大丝杠侧周向侧隙。因此, 在PRSM设计过程中, 应综合考虑牙侧角对啮合侧隙的影响, 牙侧角不应过小也不应过大。

图11

牙侧角对PRSM轴向侧隙影响

图12

牙侧角对PRSM径向侧隙影响

图13

牙侧角对PRSM周向侧隙影响

4.2.3 牙厚

图 14~16为螺纹牙厚对PRSM轴向、径向以及周向侧隙的影响。从图 14~16可以看出螺纹牙厚越大, 滚柱与丝杠侧及螺母侧在轴向、径向及周向3个方向的啮合侧隙均在减小。可以通过增大滚柱、丝杠及螺母上螺纹牙厚降低啮合侧隙, 甚至实现无侧隙啮合, 但是过大的螺纹牙厚可能会导致三者无法装配，应根据实际需要设计。因此, 适当增大螺纹牙厚有利于降低PRSM啮合侧隙。

图14

螺纹牙厚对PRSM轴向侧隙影响

图15

螺纹牙厚对PRSM径向侧隙影响

图16

螺纹牙厚对PRSM周向侧隙影响

5 结论

本文对行星滚柱丝杠在不同方向上啮合特性进行分析, 基于空间曲面接触条件和螺纹曲面方程, 推导了PRSM在轴向、径向以及周向上啮合点位置和啮合侧隙, 并分析了结构参数等对PRSM不同方向上啮合特性的影响规律, 得出了以下结论:

1) 滚柱与丝杠侧在轴向、径向以及周向上的啮合点均不在名义中径处, 滚柱与螺母侧在3个方向上的啮合点均在滚柱名义中径位置, 但只有轴向、周向上的啮合点在螺母名义中径位置。

2) 随着零件螺距的增大, 丝杠侧轴向、径向侧隙均增大, 周向侧隙减小; 螺母侧轴向、径向侧隙先增大后减少, 周向侧隙不变。适当增大或者降低螺距, 能够有效减小PRSM啮合侧隙。

3) 增大零件螺纹牙侧角, 会增大丝杠侧轴向、周向侧隙, 然而径向侧隙先增大后基本不变; 对于螺母侧, 降低其径向侧隙, 不改变轴向、周向侧隙。

4) 螺纹牙厚增大时, 丝杠侧、螺母侧在轴向、径向以及周向啮合侧隙均下降, 可通过增大牙厚实现PRSM无侧隙啮合, 这对PRSM设计具有一定的指导意义。

References

YAO Q, ZHANG M, LIU Y , et al. Multi-objective optimization of planetary roller screw mechanism based on improved mathematical modelling[J]. Tribology International, 2021, 161: 107095. [Article] [CrossRef] [Google Scholar]
QIAO Guan, LIU Geng, MA Shangjun. Principal curvature calculation and contact characteristics analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Engineering, 2020, 56(21): 140–148. [Article] (in Chinese) [CrossRef] [Google Scholar]
MENG J J, DU X, LI Y M, et al. A multiscale accuracy degradation prediction method of planetary roller screw mechanism based on fractal theory considering thread surface roughness[J]. Fractal and Fractional, 2021, 5(4): 1–20 [Google Scholar]
GRUSZECKI J, GRZYBOWSKI J, RZUCIDLO P. Electro-mechanical actuators for general aviation fly-by-wire aircraft[J]. Aviation, 2005, 9: 19–25 [CrossRef] [Google Scholar]
LIU Y Q, WANG J S, CHENG H X. Kinematics analysis of the roller screw based on the accuracy of meshing point calculation[J]. Mathematical Problems in Engineering, 2015, 2015: 303972 [Google Scholar]
ANDRADE A, NICOLOSI D, LUCCHI J, et al. Auxiliary total artificial heart: a compact electromechanical artificial heart working simultaneously with the natural heart[J]. Artificial Organs, 1999, 23: 876–880. [Article] [CrossRef] [Google Scholar]
ZHOU G W, ZHANG Y H, WANG Z Z, et al. Analysis of transient mixed elastohydrodynamic lubrication in planetary roller screw mechanism[J]. Tribology International, 2021, 163: 107158. [Article] [CrossRef] [Google Scholar]
ABEVI F, DAIDIE A, CHAUSSUMIER M, et al. Static load distribution and axial stiffness in a planetary roller screw mechanism[J]. Journal of Mechanical Design, 2016, 138: 012301. [Article] [CrossRef] [Google Scholar]
DU X, CHEN B, ZHENG Z. Investigation on mechanical behavior of planetary roller screw mechanism with the effects of external loads and machining errors[J]. Tribology International, 2021, 154: 106689. [Article] [CrossRef] [Google Scholar]
AUREGAN G, FRIDRICI V, KAPSA P, et al. Experimental simulation of rolling-sliding contact for application to planetary roller screw mechanism[J]. Wear, 2015, 332/333: 1176–1184. [Article] [CrossRef] [Google Scholar]
LI L J, FU Y L, ZHENG S C, et al. Friction torque analysis of planetary roller screw mechanism in roller jamming[J]. Mathematical Problems in Engineering, 2020(12): 1392380 [Google Scholar]
QIAO G, LIU G, MA S J, et al. Thermal characteristics analysis and experimental study of the planetary roller screw mechanism[J]. Applied Thermal Engineering, 2019, 149: 1345–1358. [Article] [CrossRef] [Google Scholar]
LI X, LIU G, FU X J, et al. Review on motion and load-bearing characteristics of the planetary roller screw mechanism[J]. Machines, 2022, 10(317): 1–15 [Google Scholar]
VELINSKY S A, CHU B, LASKY T A. Kinematics and efficiency analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Design, 2009, 131: 011016. [Article] [CrossRef] [Google Scholar]
CAI W, LIU G, MA S J, et al. A dynamic separable convolution RCNN for lubrication condition identification of planetary roller screw mechanism[J]. Advances in Mechanical Engineering, 2022, 14(4): 1–15 [Google Scholar]
ZHAO Ying, NI Jie, LYU Lina, et al. Mesh calculation of roller screw pair[J]. Journal of Machine Design, 2003, 20(3): 34–35. [Article] (in Chinese) [Google Scholar]
JONES M H, VELINSKY S A. Contact kinematics in the roller screw mechanism[J]. Journal of Mechanical Design, 2013, 135: 051003. [Article] [CrossRef] [Google Scholar]
FU Xiaojun, LIU Geng, MA Shangjun, et al. Studies on meshing mechanism of helical surfaces in planetary roller screw mechanism[J]. Journal of Mechanical Engineering, 2016, 52(3): 26–33. [Article] (in Chinese) [Google Scholar]
SANDU S, BIBOULET N, NELIAS D, et al. An efficient method for analyzing the roller screw thread geometry[J]. Mechanism and Machine Theory, 2018, 126: 243–264. [Article] [CrossRef] [Google Scholar]
CHEN Shiyun, FAN Yuanxun, LEI Jianjie. Mesh calculation and interference elimination of the planetary roller screw[J]. Modular Machine Tool and Automatic Manufacturing Technique, 2018(8): 4–7. [Article] (in Chinese) [Google Scholar]
LIU Jingnan, FAN Yuanxun. Study on load meshing model of planetary roller screw considering errors[J]. Mechine Building and Automation, 2021, 50(6): 143–147. [Article] (in Chinese) [Google Scholar]

All Tables

PRSM结构参数

轴向啮合点位置与间隙对比结果

All Figures

	图1 PRSM结构组成
In the text

	图2 PRSM零件坐标系和螺纹牙轮廓坐标系
In the text

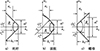	图3 PRSM螺纹牙轮廓
In the text

	图4 PRSM在全局坐标系位置关系
In the text

	图5 空间曲面位置关系
In the text

	图6 丝杠与滚柱侧啮合点位置
In the text

	图7 螺母与滚柱侧啮合点位置
In the text

	图8 螺距对PRSM轴向侧隙影响
In the text

	图9 螺距对PRSM径向侧隙影响
In the text

	图10 螺距对PRSM周向侧隙影响
In the text

	图11 牙侧角对PRSM轴向侧隙影响
In the text

	图12 牙侧角对PRSM径向侧隙影响
In the text

	图13 牙侧角对PRSM周向侧隙影响
In the text

	图14 螺纹牙厚对PRSM轴向侧隙影响
In the text

	图15 螺纹牙厚对PRSM径向侧隙影响
In the text

	图16 螺纹牙厚对PRSM周向侧隙影响
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] YAO Q, ZHANG M, LIU Y , et al. Multi-objective optimization of planetary roller screw mechanism based on improved mathematical modelling[J]. Tribology International, 2021, 161: 107095. [Article] [CrossRef] [Google Scholar]

[2] QIAO Guan, LIU Geng, MA Shangjun. Principal curvature calculation and contact characteristics analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Engineering, 2020, 56(21): 140–148. [Article] (in Chinese) [CrossRef] [Google Scholar]

[3] MENG J J, DU X, LI Y M, et al. A multiscale accuracy degradation prediction method of planetary roller screw mechanism based on fractal theory considering thread surface roughness[J]. Fractal and Fractional, 2021, 5(4): 1–20 [Google Scholar]

[4] GRUSZECKI J, GRZYBOWSKI J, RZUCIDLO P. Electro-mechanical actuators for general aviation fly-by-wire aircraft[J]. Aviation, 2005, 9: 19–25 [CrossRef] [Google Scholar]

[5] LIU Y Q, WANG J S, CHENG H X. Kinematics analysis of the roller screw based on the accuracy of meshing point calculation[J]. Mathematical Problems in Engineering, 2015, 2015: 303972 [Google Scholar]

[6] ANDRADE A, NICOLOSI D, LUCCHI J, et al. Auxiliary total artificial heart: a compact electromechanical artificial heart working simultaneously with the natural heart[J]. Artificial Organs, 1999, 23: 876–880. [Article] [CrossRef] [Google Scholar]

[7] ZHOU G W, ZHANG Y H, WANG Z Z, et al. Analysis of transient mixed elastohydrodynamic lubrication in planetary roller screw mechanism[J]. Tribology International, 2021, 163: 107158. [Article] [CrossRef] [Google Scholar]

[8] ABEVI F, DAIDIE A, CHAUSSUMIER M, et al. Static load distribution and axial stiffness in a planetary roller screw mechanism[J]. Journal of Mechanical Design, 2016, 138: 012301. [Article] [CrossRef] [Google Scholar]

[9] DU X, CHEN B, ZHENG Z. Investigation on mechanical behavior of planetary roller screw mechanism with the effects of external loads and machining errors[J]. Tribology International, 2021, 154: 106689. [Article] [CrossRef] [Google Scholar]

[10] AUREGAN G, FRIDRICI V, KAPSA P, et al. Experimental simulation of rolling-sliding contact for application to planetary roller screw mechanism[J]. Wear, 2015, 332/333: 1176–1184. [Article] [CrossRef] [Google Scholar]

[11] LI L J, FU Y L, ZHENG S C, et al. Friction torque analysis of planetary roller screw mechanism in roller jamming[J]. Mathematical Problems in Engineering, 2020(12): 1392380 [Google Scholar]

[12] QIAO G, LIU G, MA S J, et al. Thermal characteristics analysis and experimental study of the planetary roller screw mechanism[J]. Applied Thermal Engineering, 2019, 149: 1345–1358. [Article] [CrossRef] [Google Scholar]

[13] LI X, LIU G, FU X J, et al. Review on motion and load-bearing characteristics of the planetary roller screw mechanism[J]. Machines, 2022, 10(317): 1–15 [Google Scholar]

[14] VELINSKY S A, CHU B, LASKY T A. Kinematics and efficiency analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Design, 2009, 131: 011016. [Article] [CrossRef] [Google Scholar]

[15] CAI W, LIU G, MA S J, et al. A dynamic separable convolution RCNN for lubrication condition identification of planetary roller screw mechanism[J]. Advances in Mechanical Engineering, 2022, 14(4): 1–15 [Google Scholar]

[16] ZHAO Ying, NI Jie, LYU Lina, et al. Mesh calculation of roller screw pair[J]. Journal of Machine Design, 2003, 20(3): 34–35. [Article] (in Chinese) [Google Scholar]

[17] JONES M H, VELINSKY S A. Contact kinematics in the roller screw mechanism[J]. Journal of Mechanical Design, 2013, 135: 051003. [Article] [CrossRef] [Google Scholar]

[18] FU Xiaojun, LIU Geng, MA Shangjun, et al. Studies on meshing mechanism of helical surfaces in planetary roller screw mechanism[J]. Journal of Mechanical Engineering, 2016, 52(3): 26–33. [Article] (in Chinese) [Google Scholar]

[19] SANDU S, BIBOULET N, NELIAS D, et al. An efficient method for analyzing the roller screw thread geometry[J]. Mechanism and Machine Theory, 2018, 126: 243–264. [Article] [CrossRef] [Google Scholar]

[20] CHEN Shiyun, FAN Yuanxun, LEI Jianjie. Mesh calculation and interference elimination of the planetary roller screw[J]. Modular Machine Tool and Automatic Manufacturing Technique, 2018(8): 4–7. [Article] (in Chinese) [Google Scholar]

[21] LIU Jingnan, FAN Yuanxun. Study on load meshing model of planetary roller screw considering errors[J]. Mechine Building and Automation, 2021, 50(6): 143–147. [Article] (in Chinese) [Google Scholar]