| Issue |
JNWPU
Volume 41, Number 4, August 2023
|
|
|---|---|---|
| Page(s) | 670 - 678 | |
| DOI | https://doi.org/10.1051/jnwpu/20234140670 | |
| Published online | 08 December 2023 | |
Study on the meshing theory of the ring-shaped roller screw mechanism
环形牙滚柱丝杠啮合机理研究
Received:
1
September
2022
Based on the structural characteristics of ring-shaped roller screw mechanism (RRSM), helical equations of the screw, roller and nut are derived. Meshing equations at the screw-roller and nut-roller interfaces are developed, which can be used to calculated contact positions of thread teeth. The equations of axial clearances in the RRSM are also derived and zero-clearance design values of the thread thicknesses are given. By comparing the contact positions and clearances obtained from a previously published numerical model, the feasibility of the proposed model is validated. The influence of structural parameters on the meshing characteristics of the RRSM is analyzed. When the nominal radius of the screw is increased or that of the roller is decreased, the contact point at the screw-roller interface will move towards to the tangential-point of pitch circles. The difference between the value of the screw flank angle and that of the screw flank angle has great influence on contact positions. When the values of the nut and roller flank angles are equal, the contact points will lie on the tangential-point of pitch circles and the zero-clearance design value of the thread thickness at the nut-roller interface is equal to the half of the screw pitch. The radius of the roller thread profile has little influence on the zero-clearance design values of thread thickness.
摘要
基于环形牙滚柱丝杠结构特点, 推导了丝杠、滚柱和螺母的曲面方程, 建立了计算丝杠和滚柱以及螺母和滚柱之间接触位置的啮合方程, 给出了环形牙滚柱丝杠的轴向间隙计算公式和零间隙牙厚设计量。通过与现有数值模型接触位置和间隙计算结果的对比, 验证了所建模型的正确性, 分析了结构参数对环形牙滚柱丝杠啮合特性的影响规律。分析结果表明: 较大的丝杠名义半径和较小的滚柱名义半径有利于接触点接近两零件中径切点位置; 丝杠和滚柱的接触位置对两零件的牙侧角差值十分敏感; 当螺母和滚柱牙侧角相同时, 接触点位于两者的中径切点且零间隙牙厚设计量等于螺距的一半; 滚柱牙型轮廓半径对丝杠和滚柱的零间隙牙厚设计量几乎无影响。
Key words: roller screw mechanism / ring-shaped tooth / helical surface / contact position / clearance
关键字 : 滚柱丝杠 / 环形牙 / 螺旋曲面 / 接触位置 / 间隙
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
环形牙滚柱丝杠(ring-shaped roller screw mechanism, RRSM)是一种通过具有环形凸牙的滚柱与具有环形凹牙的螺母和多头丝杠啮合将旋转运动转化为直线运动的螺旋传动机构。由于采用滚柱作为丝杠和螺母的传力零件, RRSM具有与行星滚柱丝杠相同的高承载、长寿命和高精度优点。此外, 因为采用环形牙结构, 保证了滚柱相对螺母无轴向运动, 且滚柱直径无需随着丝杠直径的增加而增加。因此, 在重载工况下, RRSM与行星滚柱丝杠相比具有更小的径向尺寸与质量。RRSM在重型车辆、大型船舶、海洋装备和冶金机械等领域有着广阔的应用前景。
现有研究多以行星滚柱丝杠为对象进行, 主要集中于承载特性[1-2]、运动学分析[3-4]、动力学分析[5-6]和摩擦润滑[7]等。在啮合机理研究方面, Blinov等[8]通过在丝杠和滚柱以及螺母和滚柱轴向重叠区域中划分多个网格, 将曲面啮合问题转化为计算大量网格节点处轴向距离的数值问题, 讨论了滚柱名义半径增加对接触位置和轴向间隙的影响规律。Jones等[9]利用螺旋曲线的Frenet坐标系推导了计算丝杠、滚柱和螺母之间接触位置的啮合方程, 并分析了螺纹牙型参数对接触特性的影响规律。结果表明, 增加滚柱牙型轮廓半径能够有效提高行星滚柱丝杠的接触强度。使用中径螺旋升角代替接触点处螺旋升角, Liu等[10-11]给出了计算接触位置的啮合方程, 并对比了滚柱牙型轮廓曲线分别为圆弧、椭圆和抛物线时行星滚柱丝杠的接触位置。徐强等[12]根据啮合区域的空间几何关系, 建立了差动式行星滚柱丝杠的空间啮合模型。Fu等[13]基于丝杠、滚柱和螺母的螺旋曲面方程, 推导了能够考虑制造和装配误差的行星滚柱丝杠啮合方程, 并分析了零件偏斜对接触位置和间隙的影响规律。刘佳等[14]采用类似Blinov模型[8]的数值方法计算了行星滚柱丝杠螺纹牙的接触位置和在接触区域附近的间隙变化。Xing等[15]利用螺纹螺旋曲面方程计算了丝杠和滚柱以及螺母和滚柱接触位置, 并研究了结构参数对行星滚柱丝杠磨损特性的影响。上述数值模型计算效率低, 解析模型中的啮合方程仅适用于特定结构滚柱丝杠的啮合特性分析, 缺乏面向RRSM结构和啮合特点的啮合机理研究。然而, 通过啮合机理研究所获得RRSM接触位置和间隙计算结果, 是进一步实现该传动机构结构参数匹配设计、强度刚度计算、运动学与动力学分析和寿命预估的基础。
本文根据RRSM的结构和啮合特点, 建立丝杠、滚柱和螺母的螺旋曲面方程。推导了用于计算丝杠和滚柱以及螺母和滚柱之间接触位置的啮合方程。根据啮合方程, 提出了保证RRSM正确啮合的结构参数约束条件。给出RRSM轴向间隙以及零间隙牙厚设计量的计算公式。对比了本文解析公式和现有数值模型的接触位置和轴向间隙计算结果。分析了结构参数对RRSM啮合特性的影响规律。
1 结构组成和曲面方程
1.1 结构组成
RRSM的结构组成如图 1所示, 主要由外环形滚柱(见图 2a))、内环形螺母(见图 2b))、多头螺纹丝杠、内齿圈和保持架组成。多个滚柱被保持架分隔, 且均匀分布在丝杠周围。滚柱环形凸牙同时与丝杠螺纹和螺母环形凹牙相啮合。当丝杠旋转时, 滚柱在螺母内部做纯滚动运动; 丝杠螺旋曲面与滚柱环形曲面相啮合, 驱动滚柱和螺母沿轴向移动。
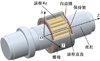 |
图1 环形牙滚柱丝杠的结构组成 |
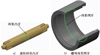 |
图2 环形牙结构 |
RRSM取消了滚柱和螺母的螺纹结构, 所以滚柱始终和螺母无相对轴向运动。因此, 螺母名义半径rN和滚柱名义半径rq之间无需满足rN=nSrq的比例关系约束, 其中nS为丝杠头数。同时, 丝杠名义半径rS和滚柱名义半径rq之间也无需满足rq=rS/(nS-2)的比例关系约束。因此, 在RRSM中, 滚柱名义半径可远小于丝杠名义半径, 从而能够极大地缩小整个传动机构的径向尺寸并减轻其质量。为了描述丝杠、滚柱和螺母之间的相对位置, 建立如图 1所示的固定坐标系O-XYZ。Z轴与丝杠轴线重合, X轴与滚柱#q的轴线相交, q=1, 2, …, nroller, nroller表示滚柱的数量。螺母为如图 2b)所示的环形凹牙结构, 磨削时无需考虑砂轮轴倾斜角问题。螺母磨削难度不随丝杠螺纹头数的增加而增加。
图 3a)~3b)分别给出了RRSM在丝杠和滚柱以及螺母和滚柱之间通过接触点的剖面。ΠSU和ΠSB表示丝杠螺纹的上下螺旋曲面; ΠqU和ΠqB分别表示滚柱环形牙的上下曲面; ΠNU和ΠNB分别表示螺母环形牙的上下曲面。如图 3a)所示, 丝杠与滚柱接触点将偏离两者轴线所形成的平面。如图 3b)所示, 螺母与滚柱接触点位于两者轴线所形成的平面内。依据受力方向的不同, 螺母所受的外部负载能够通过ΠNU→ΠqB→ΠqU→ΠSB或者ΠNB→ΠqU→ΠqS→ΠSU路径传递给丝杠。
 |
图3 丝杠和滚柱以及螺母和滚柱的接触点剖面 |
1.2 曲面方程
丝杠、滚柱和螺母的轴截面分别如图 4a)~4c)所示。oi-xiyizi为零件坐标系, i=S, N, q表示丝杠、螺母或滚柱#q。ri, ci和βi(i=S, N, q)分别表示零件的名义半径、半牙厚和牙侧角。P表示丝杠螺距或滚柱和螺母的环形牙牙距。设图 4a)中xS轴与丝杠第1条螺纹相交, 则丝杠第j条螺纹在坐标系oS-xSySzS中的螺旋曲面方程为
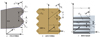 |
图4 丝杠、滚柱和螺母的轴截面 |
式中, j=1, 2, …, nS, nS为丝杠头数; uS和θS为曲面坐标; ξS=1或-1分别表示曲面ΠSU或ΠSB; ϑj为第j条螺纹的相位角
图 4b)中, kq表示第kq个滚柱环形牙, kq=1, 2, …, nT, nT为环形牙数量。rTq为牙型圆弧半径。设xq轴穿过第1个滚柱环形牙的中心, 则滚柱#q的第kq个环形牙在坐标系oq-xqyqzq中的曲面方程为
式中:uq和θq为曲面坐标; ξq=1或-1分别表示曲面ΠqU或ΠqB, uTq和wTq分别表示为
图 4c)中, kN表示第kN个螺母环形牙, kN=1, 2, …, nT, nT为环形牙数量。螺母环形牙在坐标系oN-xNyNzN中的曲面方程为
式中:uN和θN为曲面坐标; ξN=1或-1分别表示曲面ΠNU或ΠNB。
丝杠、螺母和滚柱零件坐标系oi-xiyizi(i=S, N, q)在固定坐标系O-XYZ中的位置如图 5所示。零件坐标系oi-xiyizi向固定坐标系O-XYZ的变换矩阵为
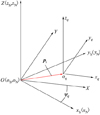 |
图5 零件坐标系与固定坐标系的位置关系 |
式中
式中, ψq为滚柱#q的相位角。
由(1)、(3)、(6)和(7)式可知, 丝杠, 螺母和滚柱曲面方程在固定坐标系O-XYZ可分别表示为
2 啮合方程
丝杠和滚柱之间接触点在XOY平面内的投影点OSq如图 6所示。rSq和rRsq分别表示丝杠和滚柱的啮合半径; ϕSq和ϕRsq分别表示丝杠和滚柱的啮合偏角。由(11)式和图 6可得, 丝杠接触点在固定坐标系O-XYZ中的位置向量可表示为
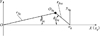 |
图6 丝杠和滚柱之间的接触位置 |
式中: zSq为丝杠接触点的Z轴坐标值; ζSq为丝杠接触点所对应的相位角
假设滚柱沿Z轴移动δSq距离后, 丝杠和滚柱相接触。由(13)式和图 6可得, 滚柱的丝杠侧接触点在固定坐标系O-XYZ中的位置向量为
式中, zRsq为滚柱未移动前所对应的接触点Z坐标值。当ξS=1时, 表示丝杠上曲面ΠSU和滚柱下曲面ΠqB相接触; 当ξS=-1时, 表示丝杠下曲面ΠSB和滚柱上曲面ΠqU相接触。
由(11)式和(14)式可得, 丝杠曲面在接触点处的外法线向量为
式中
由(13)和(16)式可得, 滚柱曲面在接触点处的外法线向量为
式中
由曲面相切接触条件可知, 丝杠和滚柱在接触点处具有相同的位置向量且外法线向量共线。由(14)~(19)式可得, 丝杠和滚柱的啮合方程为
求解(21)式能够获得丝杠和滚柱#q(q=1, 2, …, nroller)的啮合半径和啮合偏角。
为了保证RRSM的正确啮合条件, 各个滚柱应具有相同的啮合偏角和啮合半径, 即
将(22)式代入(21)式中可得
将(2)式和(10)式代入(23)式中可得
由(14)、(16)和(23)式可得, 丝杠和滚柱之间的间隙量为
当丝杠和滚柱半牙厚之和为cS+cq=c′Sq, 两者的间隙量等于δSq=0。定义c′Sq为丝杠和滚柱的零间隙牙厚设计量。由(25) 式可得
螺母和滚柱之间接触点在XOY平面内的投影点ONq如图 7所示。rNq和rRnq分别表示螺母和滚柱的啮合半径; ϕNq和ϕRnq分别表示螺母和滚柱的啮合偏角。
 |
图7 螺母和滚柱之间的接触位置 |
采用推导丝杠和滚柱啮合方程相同的方法, 可得滚柱和螺母之间的啮合方程为
式中
求解(27)式能够获得螺母和滚柱#q(q=1, 2, …, nroller) 的啮合半径和啮合偏角。由(27)式可知, 若使得螺母和滚柱的接触点位于两零件中径的切点处, 则螺母和滚柱需满足如下结构关系
将(29)~(30)式代入(27)式可得
由(3)、(6)和(31)~(33)式可得, 螺母和滚柱之间的间隙量δNq为
当螺母和滚柱半牙厚之和为cN+cq=c′Nq, 两者的间隙量δNq=0。定义c′Nq为螺母和滚柱的零间隙牙厚设计量。由(34) 式可得
3 模型验证
Blinvo等[8]在丝杠和滚柱螺纹牙轴向重叠区域内划分多个网格, 通过计算大量网格节点处滚柱曲面与丝杠曲面的zPq坐标差的最小值, 进而获得丝杠和滚柱之间的接触位置和轴向距离。虽然Blinvo等仅计算了行星滚柱丝杠的啮合特性, 但该方法也适用于RRSM的啮合特性分析。
一组RRSM的基本结构参数如表 1所示。采用本文模型和Blinvo模型[8]计算得到的丝杠和滚柱以及螺母和滚柱之间的接触位置和间隙量如表 2所示。Δu和Δθ分别表示Blinvo模型网格的径向增量和周向增量。在表 2中给出了每次分析的计算时间(CPU型号: Intel(R) Xeon(R) Gold 6230R)。本文模型的计算时间为0.031 s。当网格划分的精度逐步提高时, Blinvo模型计算结果将趋近于本文模型的计算结果。于此同时, Blinvo模型的计算时间也在大幅增加。当Δu=10-2 mm, Δθ=(10-2)°时, Blinvo模型的计算时间为0.514 s; 当Δu=10-3 mm, Δθ=(10-3)°时, 该模型计算时间达到了47.687 s。因此, 本文模型能够实现RRSM啮合特性的快速准确计算。
RRSM基本结构参数
不同啮合模型的计算结果和计算时间
4 结构参数对啮合特性的影响
4.1 丝杠名义半径和头数
当rS=20, 30和40 mm时, 丝杠和滚柱在不同丝杠头数下的接触位置变化如图 8a)~8c)所示。由螺母和滚柱之间的啮合方程(27)式可知, 当螺母的名义半径始终满足(29)式且螺母和滚柱具有相同牙侧角时, 不论丝杠中径rS如何变化, 螺母和滚柱之间的接触点始终位于两零件的中径切点位置。
 |
图8 当rS=20, 30和40 mm时, 丝杠和滚柱在不同丝杠头数下的接触位置 |
由图 8可得, 丝杠曲面ΠSU上的接触点位于坐标系xPqoPqyPq的第一象限。曲面ΠSB上的接触点位于第四象限, 且和曲面ΠSU的接触点关于xPq轴对称。因此, 在不考虑误差状态下, 丝杠两曲面ΠSU和ΠSB所对应的接触点具有相同的啮合半径和啮合偏角。在图 8a)中, 坐标(20, 0)为滚柱和丝杠中径的切点位置。当丝杠名义半径rS不变且丝杠头数nS增加时, 接触点近似沿着yPq轴远离切点位置(20, 0)。对比图 8a)~8c)可得, 若丝杠头数不变且其名义半径增加时, 接触点逐渐接近丝杠和滚柱中径的切点位置。
当rS=20~50 mm, 丝杠头数nS=6, 13, 18和21时, 丝杠和滚柱之间的零间隙牙厚设计量如图 9所示。虚线代表丝杠头数无限制下的数据值。由(35)式可知, 不考虑加工和装配误差时, 螺母和滚柱之间的零间隙牙厚设计量始终等于丝杠螺距或者螺母牙距P的一半, 即c′Nq=P/2。
 |
图9 当rS=20~50 mm时, 丝杠和滚柱在不同丝杠头数下的零间隙牙厚设计量 |
由图 9可知, 在RRSM中, 当滚柱名义半径rq不变时, 丝杠头数的最大值将受到装配空间的限制。丝杠和滚柱之间的零间隙牙厚设计量c′Sq始终小于丝杠螺距P的一半。当丝杠中径增加时或丝杠头数减小时, c′Sq的值随之增加。
4.2 滚柱名义半径和牙型轮廓半径
当滚柱名义半径rq=5, 7.5, 10 mm且滚柱牙型轮廓半径rTq∈[5, 85]mm时, 滚柱和丝杠之间的接触点位置如图 10所示。图中同时绘制了不同滚柱名义半径所对应的中径曲线。当滚柱名义半径rq增加时, 接触点将沿着yPq轴偏离丝杠和滚柱中径的切点处(30, 0)。当滚柱牙型轮廓半径rTq增加时, 接触点将沿着xPq轴向丝杠牙底圆缓慢偏移。
 |
图10 当rq=5, 7.5, 10 mm时, 丝杠和滚柱在不同滚柱螺纹牙轮廓半径下的接触位置 |
当rq=5, 7.5, 10 mm且rTq=5~85 mm时, 滚柱和丝杠之间的零间隙牙厚设计量c′Sq如图 11所示。滚柱牙型轮廓半径对c′Sq几乎没有影响。当滚柱名义半径rq增加时, c′Sq随之减小。因此, 在RRSM设计过程中应尽量选择较小的滚柱名义半径。同时, 可通过增大滚柱牙型轮廓半径rTq来增加接触点处的曲率半径值。
 |
图11 当rq=5, 7.5, 10 mm时, 丝杠和滚柱在不同滚柱螺纹牙轮廓半径下的零间隙牙厚设计量 |
4.3 丝杠和滚柱的牙侧角
由螺母和滚柱之间的啮合方程(27)式可知, 为了保证接触点始终位于两零件的切点处, 螺母和滚柱需具有相同的牙侧角。当滚柱牙侧角βq=30°, 45°和60°且ΔβSq=-2°, -1°, 0°, 1°和2°时, 丝杠和滚柱的接触位置如图 12所示。ΔβSq表示丝杠和滚柱的牙侧角差值, ΔβSq=βS-βq。
 |
图12 当βq=30°, 45°和60°且ΔβSq=-2°, -1°, 0°, 1°和2°时, 丝杠和滚柱之间的接触位置 |
由图 12可得, 当滚柱牙侧角βq增加时, 接触点将沿着yPq轴靠近丝杠和滚柱中径的切点处。当ΔβSq<0时, 接触点将随着ΔβSq的减小向丝杠牙顶圆快速偏移; 当ΔβSq>0时, 接触点将随着ΔβSq的增加向滚柱牙顶圆快速偏移。当ΔβSq=0时, 丝杠和滚柱的接触位置位于两者中径附近。
当滚柱牙侧角βq=30°, 45°和60°且ΔβSq=-2°~2°时, 丝杠和滚柱之间的零间隙牙厚设计量c′Sq如图 13所示。当滚柱和丝杠牙侧角同时增加时, 将引起c′Sq的增加。当两零件的牙侧角差值增加时, c′Sq将随之减小。因此, 在RRSM的设计中应使得滚柱和丝杠具有相同的牙侧角。
 |
图13 当βq=30°, 45°和60°且ΔβSq=-2°~2°时, 丝杠和滚柱的零间隙牙厚设计量 |
5 结论
1) 本文根据环形牙滚柱丝杠的结构特点, 推导了计算丝杠和滚柱以及螺母和滚柱之间接触位置的啮合方程, 给出了轴向间隙和零间隙牙厚设计量的计算方程, 提出了保证环形牙滚柱丝杠正确啮合的设计条件。通过与现有数值模型的接触位置和间隙计算结果相对比, 验证了本文解析方程的正确性。
2) 分析了结构参数对环形牙滚柱丝杠接触位置和轴向间隙等啮合特性的影响规律。结果表明, 较大的丝杠名义半径和较小的滚柱名义半径有利于接触点接近两零件的中径切点位置; 相比于滚柱名义半径, 滚柱牙型轮廓半径对接触位置的影响较小; 丝杠和滚柱之间的接触位置对两零件的牙侧角差值十分敏感。当螺母和滚柱牙侧角相同时, 两零件的接触点位于中径切点位置。
3) 不考虑加工和装配误差时, 螺母和滚柱之间的零间隙牙厚设计量等于丝杠螺距的一半。丝杠和滚柱之间的零间隙牙厚设计量小于丝杠螺距的一半。丝杠名义半径增加、滚柱名义半径减小或丝杠和滚柱牙侧角同时增加时, 两零件之间的零间隙牙厚设计量随之增加。滚柱牙型轮廓半径对零间隙牙厚设计量几乎无影响, 而丝杠和滚柱牙侧角的差值对其有着显著的影响。
References
- FU X J, LI X, MA S J, et al. A multi-roller static model of the planetary roller screw mechanism considering load sharing[J]. Tribology International, 2022, 173(2022): 107648-1–15 [Google Scholar]
- DU X, Chen B K, ZHENG Z D. Investigation on mechanical behavior of planetary roller screw mechanism with the effects of external loads and machining errors[J]. Tribology International, 2021, 154(2021): 106689-1–12 [Google Scholar]
- FU X J, LIU G, MA S J, et al. Kinematics model of planetary roller screw mechanism with run-out and position errors[J]. ASME Journal of Mechanical Design, 2018, 140(1): 032301-1–10 [Google Scholar]
- JONES M H, VELINSKY S A. Kinematics of roller migration in the planetary roller screw mechanism[J]. ASME Journal of Mechanical Design, 2012, 134(6): 061006-1–6 [Google Scholar]
- JONES M H, VELINSKY S A, LASKY T A. Dynamics of the planetary roller screw mechanism[J]. ASME Journal of Mechanisms and Robotics, 2016, 8(1): 014503-1–6 [Google Scholar]
- FU X J, LIU G, LI X, et al. Dynamic modeling of the double-nut planetary roller screw mechanism considering elastic deformations[J]. ASME Journal of Computational and Nonlinear Dynamics, 2021, 16(2021): 051003-1–13 [Google Scholar]
- ZHOU G W, ZHANG Y H, WANG Z Z, et al. Analysis of transient mixed elastohydrodynamic lubrication in planetary roller screw mechanism[J]. Tribology International, 2021, 163(2021): 107158-1–12 [Google Scholar]
- BLINOV D S, RYAKHOVSKY O A, SOKOLOV P A. Numerical method of determining the point of initial thread contact of two screws with parallel axes and different thread inclinations[J]. Scientific Journal of Murmansk State Technical University, 1996(3): 93–97 [Google Scholar]
- JONES M H, VELINSKY S A. Contact kinematics in the roller screw mechanism[J]. ASME Journal of Mechanical Design, 2013, 135(5): 051003-1–10 [Google Scholar]
- LIU Y Q, WANG J S, CHENG H G, et al. Kinematics analysis of the roller screw based on the accuracy of meshing point calculation[J/OL]. (2015-05-09)[2023-07-14]. https://www.hindawi.com/journals/mpe/2015/303972/ [Google Scholar]
- LIU Y Q, SHANG Y, WANG J S. Mathematical analysis of the meshing performance of planetary roller screws applying different roller thread shapes[J]. Advances in Mechanical Engineering, 2017, 9(5): 1–11 [Google Scholar]
- XU Qiang, WANG Shuiming, ZHAO Guoping, et al. The analysis of meshing interference and elimination of PWG planetary roller screw[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015(9): 107–109 [Article] (in Chinese) [Google Scholar]
- FU X J, LIU G, MA S J, et al. A comprehensive contact analysis of planetary roller screw mechanism[J]. ASME Journal of Mechanical Design, 2017, 139(1): 012302-1–11 [Google Scholar]
- LIU Jia, PENG Hang, LUO Ying, et al. Research on contact shape function and contact model of planetary roller screw drive pair[J]. Nuclear Power Engineering, 2021, 42(2): 180–182 [Article] (in Chinese) [Google Scholar]
- XING M C, ZHANG B H, DENG P, et al. A novel wear prediction model for planetary roller screw based on universal sliding distance model[J]. Tribology International, 2022, 175(2022): 107851-1–11 [Google Scholar]
All Tables
All Figures
 |
图1 环形牙滚柱丝杠的结构组成 |
| In the text | |
 |
图2 环形牙结构 |
| In the text | |
 |
图3 丝杠和滚柱以及螺母和滚柱的接触点剖面 |
| In the text | |
 |
图4 丝杠、滚柱和螺母的轴截面 |
| In the text | |
 |
图5 零件坐标系与固定坐标系的位置关系 |
| In the text | |
 |
图6 丝杠和滚柱之间的接触位置 |
| In the text | |
 |
图7 螺母和滚柱之间的接触位置 |
| In the text | |
 |
图8 当rS=20, 30和40 mm时, 丝杠和滚柱在不同丝杠头数下的接触位置 |
| In the text | |
 |
图9 当rS=20~50 mm时, 丝杠和滚柱在不同丝杠头数下的零间隙牙厚设计量 |
| In the text | |
 |
图10 当rq=5, 7.5, 10 mm时, 丝杠和滚柱在不同滚柱螺纹牙轮廓半径下的接触位置 |
| In the text | |
 |
图11 当rq=5, 7.5, 10 mm时, 丝杠和滚柱在不同滚柱螺纹牙轮廓半径下的零间隙牙厚设计量 |
| In the text | |
 |
图12 当βq=30°, 45°和60°且ΔβSq=-2°, -1°, 0°, 1°和2°时, 丝杠和滚柱之间的接触位置 |
| In the text | |
 |
图13 当βq=30°, 45°和60°且ΔβSq=-2°~2°时, 丝杠和滚柱的零间隙牙厚设计量 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


