| Issue |
JNWPU
Volume 38, Number 3, June 2020
|
|
|---|---|---|
| Page(s) | 619 - 626 | |
| DOI | https://doi.org/10.1051/jnwpu/20203830619 | |
| Published online | 06 August 2020 | |
Online Fault Detection of Fixed-Wing UAV Based on DKPCA Algorithm with Multiple Operation Conditions Considered
基于DKPCA的固定翼无人机多工况在线故障诊断
1
School of Ordnance Sergeant, Army Engineering University, Wuhan 430075, China
2
School of Electrical Engineering and Automation, Wuhan University, Wuhan 430072, China
Received:
2
August
2019
The mission execution process of a fixed-wing UAV has multiple phases and multiple operation conditions. Its parameters are nonlinear and dynamic. These characteristics make its online fault detection rather complicated. To carry out the fault detection, this paper selects nine key parameters of the transverse, longitudinal and velocity control loops of the UAV to characterize its real-time conditions. The core parameters are dynamically preprocessed to construct an augmented matrix so as to describe the dynamic characteristics of the UAV. Then, the improved k-mediods* algorithm is used to cluster the operation conditions of the UAVs by means of augmented dimensions. Neural networks are used to achieve the online matching of operation conditions. To overcome the nonlinearity of the UAV, the fault detection is performed by using the DKPCA algorithm; the fault monitoring is conducted through constructing the compound indexes of SPE and T2, notated as FAI. Furthermore, the fault separation algorithm is proposed to specify the variables of fault from the augmented high-dimensional data set. In order to deal with the erroneous reporting of faults due to measurement errors, the paper conducts the wavelet denoising of FAI, the compound indexes of the DKPCA algorithm. Finally, the data set collected from a real UAV flight is used to verify the effectiveness of the DKPCA algorithm for operation condition clustering and matching, fault detection and wavelet denoising.
摘要
固定翼无人机（UAV）执行任务过程包含多个阶段，体现出多工况特征，且UAV参数具有动态性和非线性，导致UAV在线故障诊断复杂化。本文选取UAV横向、纵向和速度控制回路的9个核心参数来表征无人机实时状态，通过动态预处理构建增广矩阵以描述UAV的动态特征；采用改进k-mediods*算法对UAV扩维数据进行工况聚类，并采用神经网络完成在线工况匹配。针对UAV非线性特征，采用了DKPCA算法进行故障诊断，基于SPE和T2构建合成指标FAI用于故障监测，并提出了分离算法从高维数据定位故障变量；为了应对测量误差带来的故障误报，还对DKPCA合成指标FAI进行了小波去噪处理。最后，以某UAV的实飞数据为对象，呈现以上算法的结果，验证了工况聚类、工况匹配、故障诊断及小波去噪等算法的有效性。
Key words: fixed-wing UAV / fault detection / DKPCA algorithm / operation condition clustering / multiple operation conditions
关键字 : 固定翼无人机 / 动态核主元分析 / 聚类 / 多工况 / 故障诊断
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
近年来, 随着技术的发展和市场需求的扩张, 固定翼无人机(Fixed wing unmanned aerial vehicle, 以下简称UAV)在全球军民两用领域得到了快速发展。UAV结构复杂、造价昂贵、安全飞行的影响因素多, 一旦因故障坠机将会造成重大的经济损失和难以估量的政治、军事、社会影响, 故UAV可靠性一直是研究热点问题之一。UAV系统配套有故障自检和预警功能模块, 但仅适用于对本体健康状态作定性描述, 无法定位故障源, 更不能发现UAV非器质性隐性故障。为此, 国内外学者从定量分析的角度围绕UAV故障诊断作了大量研究, 文献[1]使用卡尔曼滤波器更新神经网络权值, 并将其用于UAV传感器和执行机构在线故障检测。文献[2]将基于模型的FDI故障诊断技术用于UAV导航系统故障检测和隔离。文献[3]在主元分析故障诊断方法的基础上采用自适应阈值以解决无人机机动情况下的暂态虚警问题。文献[4]提出一种基于小波变换与等价空间结合的方法并用于无人机执行机构故障检测。通过引入平稳小波变换对残差进行多尺度滤波, 有效降低了等价空间阶数。文献[5]使用动态核主元分析方法对单一工况UAV传感器和执行机构故障进行监测, 利用重构贡献图的方法实现了故障分离。
文献调研表明, 基于定量分析的故障诊断在UAV稳态\准稳态过程中可获得较好效果, 但在动态状态下难以取得满意结果。实际上, UAV执行任务全流程包含起飞、巡航、遂行任务、返航、回收等多个阶段, 属于典型的多工况过程。多工况间UAV各传感器和执行机构工作状态差异较大, 若使用单一的模型描述UAV多工况问题必然会导致故障错报。故开展UAV多工况在线故障诊断研究具有重要的现实意义和实用价值。
为解决以上问题, 同时考虑不依赖先验知识, 本文将基于非监督学习的改进型k-中心值(k-mediods*)聚类分析、神经网络模式识别、小波去噪与动态核主元分析(dynamic kernel principal component analysis, DKPCA)算法结合, 提出UAV在线故障诊断解决方案。该方案能够在线匹配UAV工况模型, 监控UAV各工况下工作状态, 输出故障贡献图, 定位故障源。
1 UAV状态表征及多工况分析
1.1 UAV状态及动态预处理
UAV的核心控制回路包括纵向控制、横向控制和速度控制。本文从这3个核心控制回路中选取6个传感器和3个执行器信号为关键数据, 用于后续工况分析和故障诊断。这9维数据分别是:升降舵偏角(δZ)、左副翼舵偏角(δX1)、右副翼舵偏角(δX2)、航向角(Ψ)、俯仰角(θ)、倾斜角(Φ)、高度(H)、空速(V)和缸温(T)。这9维数据涵盖了UAV核心参数, 可充分描述UAV状态。将一次数据采样构成向量, 记作x=[δz, δX1, δX2, Ψ, θ, Φ, H, V, T]∈R9；令采样次数为n, 则UAV飞行数据矩阵可记作X=[x1, x2, …, xn]∈Rn×9。
从控制系统角度看, UAV状态转移与时间有关, 属于动态系统。若直接用飞行数据矩阵X进行模型训练, 则模型无法反映样本之间的时间属性和UAV的动态特征, 属于静态模型。只有当UAV进入稳态或准稳态时, 静态模型才适用。为了体现采样的时间相关性, 反映UAV的动态性, 本文将对原始数据采样矩阵X进行动态预处理, 通过扩维构建增广矩阵
式中：D为扩维后的增广矩阵; L∈n+为扩维因子, 扩维后的数据维度为9×(L+1);T∈n+为时滞因子, 反应各变量的时延特征; xt+T+1表示取从t采样时刻起间隔T个采样后的数据。
1.2 UAV多工况分析
UAV飞行状态包含多个工况, 且工况数量不能提前获知。若以某一变量为主导对UAV进行工况划分, 则不同的变量会得到不同的结果。从图 1中可以看出, UAV的一个完整任务过程按高度变化可分为爬升、平飞、俯冲3种工作状态; 按倾斜角变化可分为左倾斜、右倾斜和直飞3种工作状态, 且这些工作状态交替出现, 导致UAV工况复杂化。例如, 从高度来看, UAV在数据帧(F)6 000~10 000 F区间保持平飞, 但倾斜角在左倾斜、右倾斜、直飞3个工况间反复切换, 考虑到UAV核心参数涉及9个变量, 仅以某一变量或少数几个变量为主导对UAV工况进行组合式划分, 会丢失大量的工况信息造成误判, 并且也不符合应用实际。
聚类是数据挖掘的一种常用方法, 能够根据数据中描述对象及其关系的信息, 将数据分成不同的簇, 适合用来对UAV多工况进行分析。k-mediods聚类是一种常用的非监督聚类算法, 该算法首先随机选取簇中心点, 再通过迭代处理更新簇中心, 直至簇中心点不再改变[6]。传统k-mediods中距离度量方式为欧氏距离, 难以处理UAV此类变密度数据, 需要进行适应性改进。本文将共享近邻距离(shared nearest neighbor distance, SNN_dis)与k-mediods进行结合, 替换k-mediods中的距离计算, 改进后的算法记作k-mediods*。SNN_dis只依赖于2个对象共享的近邻个数, 而不是这些近邻之间的实际距离, 能够基于点的密度自动进行缩放[7], 故改进算法k-mediods*将更加适合处理UAV数据的变密度特征。
UAV被有效划分为多个工况后, 在线故障诊断首先要完成工况匹配。由于UAV各维度数据与类别标签之间呈非线性关系, 传统基于模板的匹配方法很容易导致模型失配[8]。本文选用神经网络作为分类器对UAV进行工况匹配。将k-mediods*聚类结果作为含标签训练数据, 训练神经网络分类器模型; 使用该模型对测试数据进行在线工况匹配, 输出工况标签, 将该测试数据及工况标签存入聚类对应数据库, 更新模型。重复以上过程即可实现UAV在线工况匹配。
 |
图1 UAV飞行曲线 |
2 基于DKPCA的UAV故障诊断
PCA是用主成分表征原始数据空间的有效手段, 广泛应用于降维、故障诊断、图像压缩、模式识别、信号处理等多个领域[9], 但PCA无法处理数据的非线性关系。KPCA[10]引入了核空间概念, 将低维线性不可分问题通过核函数映射到高维空间使之线性可分, 故KPCA可有效应对非线性问题。本文使用KPCA算法对前文构建的动态增广矩阵D进行故障诊断和分离, 定义为DKPCA。
2.1 基于DKPCA的UAV故障诊断方法
通过对UAV实飞数据的特征分析, 取动态预处理参数为T=5, L=4;则UAV增广矩阵表示为D=[d1, d2, …, dn-T-L]=[c1, c2, …, c45]∈Rm×45, 这里m=n-L-T。为消除各维度数据的幅值差异, 需要按(2)式对原数据进行标准化。
式中：E(ci)为ci均值；δi为ci标准差。
定义非线性函数φ(·)将输入数据从原始数据空间映射到高维特征空间F。使用径向基核函数, 可计算映射后特征空间的内积[5, 11]。
式中：K为由Kij组成的核矩阵；K需要按(4)式进行中心化处理[12]。
式中：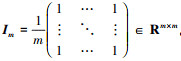
。
求解(5)式关于核矩阵K的特征方程。按照(6)式归一化特征向量v。
式中：vk为核矩阵第k个特征向量；λk为第k个特征值。
主元个数可以按照累计贡献率pCPV来确定, pCPV为核矩阵特征值累计和的百分比[11], 即
式中，λi按升序排列。一般来说, 当p个主元的CPV达到85%~95%的时候, 就认为包含了原数据的绝大部分信息。
φ(d)在特征向量vk上的映射为
式中, vik为核矩阵第k个特征值对应特征向量的第i个系数。
采用Hotelling T2和ESPE统计量来度量是否发生故障, T2及其控制限Tn2可分别由(9)至(10)式获取[13]。
式中, Λ-1为由降序排列的前p个特征值构成的对角矩阵的逆矩阵。Fp, m-p, a为p和m-p个自由度, 置信水平为1-a的F分别临界值。
ESPE及其控制限δa2可由(11)~(12)式获取。
式中: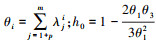 
; ca为标准正态分布在置信水平a下的阈值; p为主元个数。
实际应用中, 使用一个将ESPE和T2控制限合成的指标FFAI将更加便捷。(13)式实现了2个度量指标的融合
式中,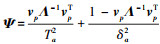 
, vp由核矩阵的前p个特征向量组成。
FFAI的控制限ζ2利用近似分布方法获得
式中,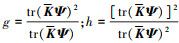 
。
以上通过合成指标FFAI实现了对故障的检测, 一旦检测到故障还需要迅速分析故障的原因, 定位导致故障的变量。KPCA算法中未指定显式的非线性变换函数, 故类似PCA的贡献图方法无法使用, 文献[14]提出了一种适合KPCA的贡献图求解过程, 其中, 测试数据矩阵各变量的故障贡献量按(15)式计算
式中：p为KPCA主元空间的主元个数；ti为第i个非线性主元；cj为D标准化后的第j个原始测量变量。具体到UAV, 其CContj为动态扩维后变量的贡献量, 尚需要将其映射到实际变量才能完成最终的故障分离。在动态预处理阶段, UAV的原始九维数据扩展为9×(L+1)维, 因此CContj中包含了(L+1)个九维原始数据的贡献量。记R为原始数据各维度故障贡献率, 用(16)式计算
式中, O_Contj为第i个九维原始数据的贡献量。DKPCA故障分离算法的伪代码如表 1所示。
DKPCA故障分离算法
2.2 统计量小波阈值去噪
过程量的测量误差会给PCA/KPCA统计量带来噪声, 对测试数据的统计量进行去噪可以有效降低故障诊断的误报率[15]。本文将采用小波去噪算法对DKPCA统计量进行处理, 提高其在UAV故障诊断中的适应性。小波阈值去噪是以小波变换为基础的一种信号处理方式。含噪信号在经过小波分解后, 不同尺度上低频信号(近似分量)与高频信号(细节分量)表征了原始信号的特征。使用合理的阈值处理方式去除各细节分量中对噪声贡献较大的成份并重构信号, 即可完成对原始信号的去噪处理[16], 得到去噪后的信号FAI′(t)。
2.3 基于DKPCA的UAV故障诊断步骤
2.3.1 故障诊断流程
基于DKPCA的故障诊断流程分为离线建模和在线诊断2个阶段。离线建模以数据预处理、扩维和聚类分析后得到的各工况下UAV无故障飞行状态数据为样本, 通过学习建立各工况的DKPCA故障诊断模型, 获取对应工况统计量的控制限。在线故障诊断阶段, 获取实时数据并完成数据预处理后, 再用训练好的神经网络分类器进行工况匹配, 提取对应工况的训练模型数据, 计算实时统计量FAI。将FAI进行小波去噪处理后与对应工况控制限ζ2进行比对。若发生故障, 则触发故障分离程序, 并定位故障源, 算法流程如图 2所示。
 |
图2 UAV故障诊断算法流程 |
2.3.2 离线建模
在离线建模阶段完成的主要步骤如下:
S1:采样数据预处理。
S2:在平行分析的基础上确定时滞因子T和扩维因子L, 构建训练样本增广矩阵D。计算D各维度均值、方差并按(2)式将数据标准化。
S3:使用k-mediods*聚类算法分析D数据, 得到各工况数据。
S4:使用聚类结果训练神经网络分类器。
S5:按(3)式计算各工况的核矩阵K, 并按(4)式中心化, 得到K。
S6:对K特征分解, 按(6)式归一化特征向量。
S7:计算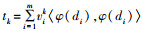
。
S8:按(14)式计算各工况下FAI阈值ζ2, 将结果按工况类标存入数据库。
2.3.3 在线故障诊断
UAV故障的在线诊断步骤如下:
S1:测试数据预处理。
S2:使用相同时滞因子T和扩维因子L, 构建测试样本增广矩阵, 使用训练样本均值和方差按(2)式对数据标准化。
S3:使用神经网络分类器判断工况归属。
S4:按(13)式计算在线FAI值。
S5:对FAI值进行小波去噪。
S6:将去噪后的FAI值与对应工况的控制阈值ζ2对比, 若FAI>ζ2, 按表 1故障分离算法计算各维度故障贡献率, 定位故障源。
3 试验验证
3.1 试验数据
为了对本文提出的算法进行验证, 从某型UAV的数据链获取了一次完整实飞数据, 共计14 757组样本。将获得的样本构成数据矩阵X, 按(1)式构建增广矩阵D, 其中T=5且L=4。
3.2 工况分类与匹配
使用k-mediods*算法对动态扩维后矩阵D进行聚类分析, 最终获得4种工况, 如图 3所示。图 3中横轴为变量数目(扩维后为45维), 纵轴为采样数, 竖轴为归一化后的变量幅值。对比图 3各子图可以发现各工况内数据高度相似且工况间数据差异较大, 表明k-mediods*算法在UAV动态数据工况划分中获得了满意结果。
从4种工况集中分别随机抽取535, 450, 500, 500组样本数据, 将其按工况1至4顺序排列构建测试数据。在测试数据的指定变量和位置刻意加入5%的正向偏移构成带故障的测试数据集fault_testdata, 如表 2所示。
带故障测试数据
将4种工况中除测试数据外的所有数据用来训练基于神经网络的工况匹配器和DKPCA模型, 再用fault_testdata验证训练好的神经网络分类器。工况分类器的输出如图 4(上)所示, 分类器成功完成了fault_testdata数据集分类, 正确率为100%。可见, 基于神经网络的工况匹配器具有一定泛化能力。
 |
图3 基于k-mediods*的UAV工况聚类 |
 |
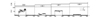图4 工况识别及故障监测结果 |
3.3 故障检出效果
按照图 2算法流程对fault_testdata进行在线故障监测, 首先使用神经网络分类器对在线测试数据工况进行匹配, 计算测试数据在适配模型下的FAI值, 并与对应工况的控制限ζ2进行对比。fault_testdata包含4种工况, 共计1 985个测试样本, 故障监测对比曲线如图 4(下)所示。结合表 2与图 4可以发现, 文章所提出的算法能够以100%的准确率检出预设故障。
为降低故障错报率, 设置当图 4(下)曲线中连续3次以上采样检测到FAI>ζ2时才触发故障报警, 之后按照表 1算法计算各维度实时故障率。图 5为工况1某时刻的故障检测指标及故障分离结果, 其中图 5a)为指标曲线, 图 5b)为故障分离结果。
为了方便观察故障分离总体效果, 将各工况分离结果按照各维度取均值, 得到各维度平均故障贡献率, 如图 6所示。对照表 2可知, 文章提出的算法能够以最大故障贡献率凸显故障变量, 能够准确定位故障维度。
 |
图5 各维度实时故障(以工况1为例) |
 |
图6 各维度平均故障贡献率 |
3.4 小波去噪
图 5还表明, FAI指标存在噪声, 体现为FAI曲线有一定波动成分, 这些波动会造成故障的误报。例如, 在图 7b)1 517采样点, UAV无故障但FAI曲线也越过了控制限。为了应对此故障误报问题, 本文采用小波阈值去噪算法对FAI进行处理, 如图 7所示。
算法参数设置如下:小波基函数选用sym5, FAI分解层数为3层, 阈值方式为软阈值, 阈值估计方式为Minimaxi[16]。在故障工况下, FAI曲线明显高于其控制限, 噪声不会对故障判断结果造成影响, 去噪后FAI曲线更加光滑且能基本保持数据原貌, 如图 7a)所示。在无故障工况下, 噪声会影响故障检出效果, 小波去噪法能起到“平滑”数据的作用, 可以防止故障误报情况发生, 如图 7b)所示。可见, 小波去噪法可降低故障误报率, 从而提高故障诊断的正确率。
 |
图7 FAI小波去噪 |
4 结论
在线故障诊断是提升固定翼UAV性能的重要手段。UAV具有动态、非线性及多工况特征, 导致在线故障诊断问题复杂化。本文以UAV3个控制回路的9个核心变量来表征UAV实时状态, 并通过动态预处理来描述UAV动态特征。针对UAV多工况特征, 采用k-mediods*聚类算法进行工况聚类并采用神经网络完成工况匹配。在在线故障诊断中采用了DKPCA以适应UAV的非线性特征, 并采用小波去噪处理FAI指标以提升算法应对测量噪声的能力。以某UAV实飞数据为对象对算法进行了验证, 结果表明:k-mediods*聚类算法将UAV实飞数据聚类为4种工况且取得了较好的聚类性能; 基于神经网络的匹配器可100%成功匹配4种工况; 在故障测试数据集上, DKPCA模型可利用合成指标FAI成功检出故障, 且提出的故障分离算法可准确定位故障; 小波去噪可有效消除测量误差对FAI指标的影响, 充分降低故障误报率。
References
- Abbaspour A, Aboutalebi P, Yen K K, et al. Neural Adaptive Observer-Based Sensor and Actuator Fault Detection in Nonlinear Systems:Application in UAV[J]. ISA Transactions, 2017, 67: 317– 329 [Article] [CrossRef] [Google Scholar]
- Lee J, Shin H, Kim T. Optimal Combination of Fault Detection and Isolation Methods of Integrated Navigation Algorithm for UAV[J]. International Journal of Aeronautical and Space Sciences, 2018, 19 (3): 694– 710 [Article] [CrossRef] [Google Scholar]
- Qiu Zongjiang, Liu Huixia, Xi Qingbiao, et al. UAV PCA Fault Detection and Diagnosis Techniques[J]. Computer Engineering and Applications, 2013, 49 (4): 262– 266 [Article](in Chinese) [Google Scholar]
- Xue Ting, Zhong Maiying, Li Gang. Wavelet Transform and Parity Space Based Actuator Fault Detection for Unmanned Aerial Vehicle[J]. Control Theory & Applications, 2016, 33 (9): 1193– 1199 [Article](in Chinese) [Google Scholar]
- Li Minghu, Li Gang, Zhong Maiying. Application of Dynamic Kernel Principal Component Analysis in Unmanned Aerial Vehicle Fault Diagnosis[J]. Journal of Shandong University, 2017, 47 (5): 215– 222 [Article](in Chinese) [Google Scholar]
- Minjuan Z. Finding Good XML Fragments Based on k-Medoid Cluster Number Optimization and Ranking Model for Feedback[C]//2013 International Conference on Information Technology and Applications, 2013: 333–337 [Google Scholar]
- Guo J, Zhao Y, Li J. A Multi-Relational Hierarchical Clustering Algorithm Based on Shared Nearest Neighbor Similarity[C]//Sixth International Conference on Machine Learning and Cybernetics, 2007: 3951–3955 [Google Scholar]
- Tang Dongming. Study on Clustering Algorithm and Its Applications[D]. Chengdu: University of Electronic Science and Technology of China, 2010(in Chinese) [Google Scholar]
- Zhang Shirong, Cheng Qin, Zhang Fangfang. Fault Detection of Motor Bearings Based on Detection Coils and KPCA Algorithm[J]. Electic Machines & Control Application, 2018, 45 (4): 98– 104 [Article](in Chinese) [Google Scholar]
- Ge Z, Yang C, Song Z. Improved Kernel PCA-Based Monitoring Approach for Nonlinear Processes[J]. Chemical Engineering Science, 2009, 64 (9): 2245– 2255 [Article] [CrossRef] [Google Scholar]
- Jaffel I, Taouali O, Harkat M F, et al. Moving Window KPCA with Reduced Complexity for Nonlinear Dynamic Process Monitoring[J]. ISA Transactions, 2016, 64: 184– 192 [Article] [CrossRef] [Google Scholar]
- Hoffmann H. Kernel PCA for Novelty Detection[J]. Pattern Recognition, 2007, 40 (3): 863– 874 [Article] [CrossRef] [Google Scholar]
- Zhang Y, Li S, Teng Y. Dynamic Processes Monitoring Using Recursive Kernel Principal Component Analysis[J]. Chemical Engineering Science, 2012, 72: 78– 86 [Article] [CrossRef] [Google Scholar]
- Deng Xiaogang, Tian Xuemin. Nonlinear Process Fault Diagnosis Method Using Kernel Principal Component Analysis[J]. Journal of Shandong University, 2005, 35 (3): 103– 106 [Article](in Chinese) [Google Scholar]
- Zhang S, Tang Q, Lin Y, et al. Fault Detection of Feed Water Treatment Process Using PCA-WD with Parameter Optimization[J]. ISA Transactions, 2017, 68: 313[J]. 326 [Article] [CrossRef] [Google Scholar]
- Cen Yigang. The Construction of a Sort of the Scalar(Multi) Wavelet and Wavelet Signal Processing[D]. Wuhan: Huazhong University of Science and Technology, 2006(in Chinese) [Google Scholar]
All Tables
All Figures
|
图1 UAV飞行曲线 |
| In the text | |
|
图2 UAV故障诊断算法流程 |
| In the text | |
|
图3 基于k-mediods*的UAV工况聚类 |
| In the text | |
|
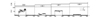图4 工况识别及故障监测结果 |
| In the text | |
|
图5 各维度实时故障(以工况1为例) |
| In the text | |
|
图6 各维度平均故障贡献率 |
| In the text | |
|
图7 FAI小波去噪 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.