Modeling and Analysis of Deformed Parafoil Recovery System

Yiming Guo; Jianguo Yan; Xiaojun Xing; Cihang Wu; Xiaoran Chen; Fenghao Li

doi:10.1051/jnwpu/20203850952

All issues

Volume 38 / No 5 (October 2020)

JNWPU, 38 5 (2020) 952-958

Full HTML

Open Access

Issue		JNWPU Volume 38, Number 5, October 2020


Page(s)		952 - 958
DOI		https://doi.org/10.1051/jnwpu/20203850952
Published online		08 December 2020

JNWPU 2020, 38(5): 952–958

Modeling and Analysis of Deformed Parafoil Recovery System

变形翼伞回收系统的建模与分析

Yiming Guo (郭一鸣), Jianguo Yan (闫建国), Xiaojun Xing (邢小军), Cihang Wu (吴慈航), Xiaoran Chen (陈潇然) and Fenghao Li (李丰浩)

School of Automation, Northwestern Polytechnical University, Xi'an 710072, China

Received: 25 November 2019

Abstract

The aerodynamic calculation of parafoil is the key technology of the parafoil recovery system modeling. In order to further improve the model accuracy, the lift coefficient and drag coefficient under the various states are obtained via fluid structure coupling method by considering the influence of the aerodynamic deformation and trailing edge deviation. Then, the least square method is used to identify the quantitative relationship among the aerodynamic coefficient, deflection, and deformation so as to improve the 6-DOF parafoil recovery system model. The results show that the structure of parafoil considering deformation and deflection is not only similar to the actual parafoil, but also the obtained aerodynamic parameters are more close to the wind tunnel test, which proves that the present method has certain significance for precisely modeling the parafoil recovery system.

摘要

翼伞的气动力计算是研究翼伞回收系统建模的关键技术问题。为了进一步提高建模精度，同时考虑了翼伞充气变形和后缘下偏量的影响，通过流固耦合方法获得各个状态下的升力系数、阻力系数。然后使用最小二乘法辨识获得气动系数和下偏量及变形之间的量化关系，改进翼伞回收系统的六自由度模型。研究表明，考虑变形及下偏情况的翼伞不仅结构和实际翼伞类似，且获得的气动参数与风洞试验更加接近，证明新方法对于翼伞回收系统精确建模的研究有一定的意义。

Key words: parafoil / fluid structure coupling / trailing edge deflection / inflatable deformation / dynamic model

关键字 : 翼伞 / 流固耦合 / 后缘下偏 / 充气变形 / 动力学模型

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

随着我国航天事业日益发展，运载火箭的发射次数不断增加。但是，由于火箭一子级分离体的落区不可控，给安全保障带来极大的困难。近年来，我国已经在长征二号丙火箭上实现了栅格舵控制，控制火箭落点在1公里范围内。然而在近地区域且速度小于1马赫数时，栅格舵控制效果微乎其微，很难进一步提高精度。因此，研究人员提出采用翼伞作为低空低速段的控制装置。

目前，国内外对翼伞动力学模型本身的研究相对成熟，但翼伞气动力计算是一个难点。飞行试验耗资巨大，因此一般采用风洞试验[1-4]及数值计算[5-8]获取翼伞气动特性。1971年NASA兰里研究中心对翼伞进行风洞试验[1]，为翼伞气动数值结果验证提供大量数据；Bergeron等[2]在DFAN亚音速风洞中，对比刚性机翼不同前缘及后缘的气动系数，为翼伞构型设计提供研究基础；邬婉楠等[5]综合考虑前缘切口及后缘下偏的影响，计算了不同切口翼伞的气动系数; 陶金等[8]采用辨识法获得翼伞不同下偏时气动参数函数，建立模型。但以上研究人员均未考虑翼伞充气变形导致的参数变化。对此，Fogell、Peralta、张思宇等[9-11]基于LS-DYNA采用显式积分算法进行翼伞变形研究，为翼伞变形提供了思路；张春等[12]基于ANSYS平台实现翼伞弱耦合变形，但缺乏进一步的参数获取。

基于以上研究工作，本文综合考虑充气变形及后缘下偏对气动系数的影响。假定翼伞有初始形状，基于ANSYS平台通过流固耦合法对稳态翼伞进行充气变形，获取各个情况下的气动系数，最后基于SIMULINK平台建立翼伞回收系统模型。

1 翼伞回收系统模型

1.1 气动模型

根据需求，设计的翼伞回收系统的初始形状及相对位置如图 1所示。

图中, 翼伞剖面采用Clark-Y的开口翼型, c为气动弦长, b为展长, R为伞绳长度, γ为展向弯曲弧度, 有12个气室组成, 每个气室相隔的肋片上开有气孔保证压力平衡; 火箭箭身长度为H, 火箭的直径为d。具体参数取值如表 1所示, m_p表示翼伞真实质量，m_r表示系统真实质量。此外, 基于欧美坐标系下, 火箭重心位置O_r相对翼伞重心位置O_p的距离为(0.53, 0, 10.6)^T。

本文采用下拉操纵绳的方法改变翼伞气动特性。一般地, 翼伞下偏会以弦长3/4处为轴偏折, 尾部1/4处发生明显偏转[5]。设置后缘偏转的程度δ和下折角度ϕ满足关系式

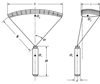图1

翼伞回收系统初始模型

表1

翼伞回收系统模型参数

1.2 动力学模型

对翼伞回收系统进行建模时, 需考虑到翼伞气动力、重力、附加质量力以及火箭气动力、重力的影响。由于稳定状态下的翼伞回收系统内部相对运动较少, 可采取常规六自由度模型进行描述。

根据动量矩定理, 得到翼伞系统的动力学方程[5]如下

式中:v, ω代表翼伞系统的速度和角速度; A代表翼伞系统质量及附加质量相加的总质量矩阵; M_a代表附加质量的矩阵; I_r和I_a分别代表真实质量和附加质量的转动惯量; L_b-p^×代表翼伞系统中心到翼伞附加质量中心的旋转矩阵; F_aero^p及M_aero^p代表翼伞部分的气动力及力矩, F_aero^r及M_aero^r代表火箭部分的气动力及力矩, F_nl及M_nl代表耦合力和力矩, F_g代表系统的总重力。其中, 翼伞部分气动力F_aero^p计算是决定建模的关键因素。

传统方法计算气动力时, 往往不考虑变形和偏转对气动系数C_L, C_D的影响, 限制了建模精度。因此, 本文综合考虑变形以及偏转, 将气动方程修正如下

式中:δ_a代表单侧下偏量; δ_e代表双侧下偏量; f_Ls(α, δ_e, δ_a)和f_Ds(α, δ_e, δ_a)代表变形修正函数

该问题转换成20个气动参数的辨识问题。此外, 由于翼伞伞衣为展向弧形翼而非平直翼, 所以伞衣气动系数呈展向椭圆分布[13], 需用微元法建立修正因子模型。首先通过CFD方法测算翼伞的修正因子, 分片从里到外对应编号1~6, 如表 2所示。

在此基础上, 将翼伞伞面微分成气动力大小均匀、方向一致的翼伞块, 如图 2所示。

采用多项式法拟合修正因子与分片位置角度γ的函数, 得到升阻力系数修正曲线为

分别计算各翼面块受到的气动力, 再对分量积分得到气动合力, 如下

式中：T_γ-o是各翼伞块基于自身压心的体坐标系与翼伞坐标系之间的变换矩阵。

综上所述, (10)、(11)式为建立系统动力学模型的翼伞气动力方程。其中, 气动系数C_L、C_D通过流固耦合变形和气动辨识相结合的方法得到。

表2

气动系数修正因子

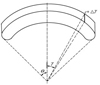图2

微元法翼伞受力示意图

2 翼伞流固耦合变形

根据飞行试验[14]可知, 翼伞在滑翔时会维持稳定形状不改变。因此, 可以采用单向流固耦合方法进行充气变形, 如图 3所示。

通过有限体积法得到初始形状翼伞在流场中的压力分布后, 采用有限元法得到翼伞的变形体, 最后再次使用有限体积法得到变形体的气动参数。

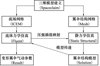图3

单向流固耦合翼伞充气变形架构

2.1 流场及结构设置

翼伞回收系统由翼伞、火箭、伞绳三部分组成, 其中, 伞绳体积较小, 在流场中可以忽略, 因此只需考虑翼伞和火箭2个扰动源。流场区域尺寸为16c×10c×16c。其中, 靠近扰动源的区域采用5c×5c×7.2c的密度盒进行网格加密, 如图 4所示。流场左侧边界为速度入口, 前后上下边界为自由滑移壁面, 右侧边界为自由流动出口。流体为不可压缩空气, 来流速度设置为30 m/s。

流场计算采用simple控制算法及二阶迎风的离散发, 提高计算精度。由于系统雷诺数在4.1×10⁶以上, 可采用标准k-ε湍流模型。控制方程如下

式中:k为湍流动能; ε为耗散率; G_k表示平均速度梯度造成的k衍生项; C_1ε^*为经验修正系数; 且有

固体部分的翼伞采用Shell 181单元建模, 材料选用1 mm的MIL-C-7020III纤维材料[15], 密度为533.8 kg·m^-3, 弹性模量为4.308×10⁸ Pa, 泊松比为0.14。采取曲率三角形划分法, 获得翼伞结构网格单元数约为5万, 节点数约为3万。

将伞衣作为耦合面, 伞衣表面压力差进行插值映射传递。由于流体和固体网格划分不同, 因此插值前后的结果略有不同。通过修改网格参数, 可将最终的加载误差降低到4%以内。

图4

流场计算网格

2.2 翼伞变形分析

选取迎角为6°时的伞衣内外表面压力差作为映射数据, 肋片为固定装置。

图 5为翼伞受到的最大主应力云图。可见, 翼伞能维持较好的刚性, 前中部区域变形较明显, 形成“鼓包”。测得上伞衣沿z轴最大变形约0.07 m, 下伞衣沿z轴最大变形约0.05 m。可见, 上下伞衣前缘区域受力较大, 且上伞衣受到的最大主应力区域明显多于下伞衣。但由于变形时将肋片作为固定约束, 弱化了变形情况。而实际情况下肋片也会发生适度弹性变形, 导致整体变形情况更加明显。

翼伞变形势必会导致翼伞升阻系数发生变化。将初始模型作为模型一, 变形模型作为模型二, 进行翼伞气动参数测量。

图5

模型受压的最大应力云图

2.3 风洞试验对比

模型一、模型二和风洞试验对比的结果如图 6所示。相较于模型一, 模型二的气动参数更接近于风洞试验测试结果。

图6

CFD仿真和风洞试验对比

2.4 气动参数辨识

CFD仿真的气动系数结果无法直接用于翼伞回收系统建模, 需采用最小二乘法进行参数辨识, 估算公式如下

式中: 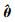为待辨识的参数矩阵; Φ代表输入矩阵; Y代表气动系数矩阵。辨识结果如表 3所示。

将辨识出的参数代入(7)~(8)式中, 获得翼伞气动系数函数, 然后建立动力学模型。

表3

气动系数辨识结果

3 仿真结果分析

3.1 后缘下偏分析

假定2个模型下偏时弯折的角度和位置类似, 对比它们在1/3, 2/3偏转程度下, 单侧或双侧下偏时的伞衣表面压力云图, 如图 7~10所示。

对比两模型压力分布, 可知由于翼伞受压突起产生的“鼓包”, 导致上翼面流动复杂化, 且在各个气室相交处产生负压极值, 前缘压力分布不均匀; 下伞衣由于变形较小, 压力分布区别较小。

单侧下偏时, 上下伞衣表面压力会发生不对称, 在下偏一端的弯折处, 上伞衣会产生负压区, 下伞衣会产生较大的正压, 伞衣的不对称性导致翼伞发生翻滚和偏航, 控制系统的横侧向运动。双侧下偏时, 上下伞衣对称且下偏端与单侧下偏时产生的现象一致, 控制系统的纵向运动。

取迎角范围为-4°~14°, 进一步对比不同情况下单、双侧下偏气动参数, 如图 11、12所示。

由图可知, 在相同的条件下, 等量双侧下偏比单侧下偏对应的气动系数变化更明显。此外, 从变化趋势来看, 两模型的阻力系数基本随偏转增大发生规律性增长; 模型一的升力系数呈现先上升后稳定的趋势, 模型二呈现先上升后下降的趋势, 模型二的失速迎角小于模型一。

单侧下偏1/3伞衣压力分布

单侧下偏2/3伞衣压力分布

双侧下偏1/3时伞衣压力分布

双侧下偏2/3时伞衣压力分布

单侧下偏气动参数对比

双侧下偏气动参数对比

3.2 动力学仿真结果

翼伞回收系统初始状态设定在高度8 000 m, 速度为30 m/s左右。采用模型二的气动参数, 在稳定滑行25 s时, 使用控制器拉动伞绳, 获得单侧下偏和双侧下偏仿真结果如图 13~14所示。除图 13d)外, 其余仿真时间为50 s。因为单侧下偏为横侧向控制输入, 双侧下偏为纵向控制输入, 所以图 13、14仅展示与当前控制相关且变化明显的状态变量。

根据仿真结果, 单侧下偏时, 翼伞回收系统会进行盘旋下降运动, 随着单侧后缘下偏量增大, 伞衣左右压力不对称现象更加明显, 进而导致滚转角增大, 偏航角变化率增大, 盘旋圆周变小; 双侧下偏时, 系统会发生减速运动, 随着两侧后缘下偏量增大, 翼伞后倾的幅度随之增大, 进而导致迎角增加, 俯仰角增大, 系统速度减小, 高度下降变慢。

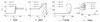图13

系统单侧下偏横侧向仿真

图14

系统双侧下偏纵向仿真

4 结论

1) 本文先将具有初始形状的翼伞回收系统进行流固耦合分析, 得到翼伞在稳态飞行中会发生一定的变形, 且伞衣前中部的区域变形明显, 沿z轴的最大变形位移可达到18%, 获得变形模型;

2) 结合后缘下偏的影响, 将初始模型和变形模型进行压力云图及气动参数对比, 可见“鼓包”会导致翼伞上伞衣压力分布不均匀, 升阻力系数上升, 升阻比下降; 单侧后缘下偏时翼伞伞衣压力分布不对称, 导致滚转和偏航。和风洞试验对比可知, 考虑变形以及后缘下偏的模型气动参数更加准确;

3) 基于变形模型的气动参数, 建立翼伞回收系统六自由度模型, 在此基础上进行了下偏仿真, 与可信度较高的参考文献仿真结果[16]以及空投试验[14]对比, 本文仿真情况趋势与之接近。因此, 采用本文的方法, 综合考虑变形及后缘下偏可以提高建模精度, 对于今后基于模型设计控制律有重要意义。

References

Nicolaides J D. Parafoil Wind Tunnel Tests[R]. Notre Dame Univ in Dept of Aerospace and Mechanical Engineering, 1971 [CrossRef] [Google Scholar]
Dowling M, Costello M. Feasibility Study of Embedded Wind Energy Harvesting System for Parafoil-Payload Aircraft[J]. Journal of Aircraft, 2018, 55(5): 2127–2136 [Article] [CrossRef] [Google Scholar]
Bergeron K, Seidel J, McLaughlin T E. Wind Tunnel Investigations of Rigid Ram-Air Parachute Canopy Configurations[C]//23rd AIAA Aerodynamic Decelerator Systems Technology Conference, 2015 [Google Scholar]
Uddin M N, Mashud O M, Waliullah T, et al. Effect of Introducing Large Scale Roughness through Static Curvature Modifications on the Low Speed Flow over an Airfoil[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, 2013 [Google Scholar]
Wannan W, Qinglin S, Mingwei S, et al. Modeling and Control of Parafoil Based on Computational Fluid Dynamics[J]. Applied Mathematical Modelling, 2019(70): 378–401 [Article] (in Chinese) [Google Scholar]
Tao J, Liang W, Sun Q L, et al. Modeling and Control of a Powered Parafoil in Wind and Rain Environments[J]. IEEE Trans on Aerospace and Electronic Systems, 2017, 53(4): 1642–1659 [Article] [CrossRef] [Google Scholar]
Ghoreyshi M, Bergeron K, Lofthouse A J, et al. CFD Calculation of Stability and Control Derivatives for Ram-Air Parachutes[C]//AIAA Atmospheric Flight Mechanics Conference, 2016 [Google Scholar]
Tao J, Sun Q L, Liang W, et al. Computational Fluid Dynamics Based Dynamic Modeling of Parafoil System[J]. Applied Mathematical Modelling, 2018(54): 136–150 [Article] (in Chinese) [CrossRef] [Google Scholar]
Fogell N, Sherwin S J, Cotter C J, et al. Fluid-Structure Interaction Simulation of the Inflated Shape of Ram-Air Parachutes[C]//27th AIAA Aerodynamic Decelerator Systems Conference, 2013 [Google Scholar]
Peralta R, Johari H. Geometry of a Ram-Air Parachute Canopy in Steady Flight from Numerical Simulations[C]//23rd AIAA Aerodynamic Decelerator Systems Technology Conference, 2015 [Google Scholar]
Zhang Siyu, Yu Li, Liu Xing. Numerical Simulation of Parafoil Inflation Process Based on Fluid-Structure Interaction Method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(6): 1108–1115 [Article] (in Chinese) [Google Scholar]
Zhang Chun, Cao Yihua. Numerical Simulation of Parafoil Aerodynamics and Structural Deformation Based on Loose Coupled Method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 605–609 [Article] (in Chinese) [Google Scholar]
Slegers N, Costello M. Aspects of Control for a Parafoil and Payload System[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(6): 898–905 [Article] [CrossRef] [Google Scholar]
Sun Qinglin, Liang Wei, Tao Jin, et al. Dynamic Modeling of Parafoil Based on CFD Simulation and Least Square[J]. Trans of Beijing Institute of Technology, 2017, 37(2): 157–162 [Article] (in Chinese) [Google Scholar]
Longfang W, Weiliang M. Analytical Study on Deformation and Structural Safety of Parafoil[J]. International Journal of Aerospace Engineering, 2018, 16: 1–7 [Article] (in Chinese) [Google Scholar]
Omprakash N A. Modeling and Simulation of 9-DOF Parafoil-Payload System Flight Dynamics[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2006 [Google Scholar]
Liu Yuan, Yan Jianguo, Li Mingjun, et al. Research on Aerodynamic Performance of Ram-Air Parafoil[J]. Flight Dynamics, 2017, 35(3): 24–27 [Article] (in Chinese) [Google Scholar]

All Tables

翼伞回收系统模型参数

气动系数修正因子

气动系数辨识结果

All Figures

	图1 翼伞回收系统初始模型
In the text

	图2 微元法翼伞受力示意图
In the text

	图3 单向流固耦合翼伞充气变形架构
In the text

	图4 流场计算网格
In the text

	图5 模型受压的最大应力云图
In the text

	图6 CFD仿真和风洞试验对比
In the text

	图7 单侧下偏1/3伞衣压力分布
In the text

	图8 单侧下偏2/3伞衣压力分布
In the text

	图9 双侧下偏1/3时伞衣压力分布
In the text

	图10 双侧下偏2/3时伞衣压力分布
In the text

	图11 单侧下偏气动参数对比
In the text

	图12 双侧下偏气动参数对比
In the text

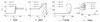	图13 系统单侧下偏横侧向仿真
In the text

	图14 系统双侧下偏纵向仿真
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Nicolaides J D. Parafoil Wind Tunnel Tests[R]. Notre Dame Univ in Dept of Aerospace and Mechanical Engineering, 1971 [CrossRef] [Google Scholar]

[2] Dowling M, Costello M. Feasibility Study of Embedded Wind Energy Harvesting System for Parafoil-Payload Aircraft[J]. Journal of Aircraft, 2018, 55(5): 2127–2136 [Article] [CrossRef] [Google Scholar]

[3] Bergeron K, Seidel J, McLaughlin T E. Wind Tunnel Investigations of Rigid Ram-Air Parachute Canopy Configurations[C]//23rd AIAA Aerodynamic Decelerator Systems Technology Conference, 2015 [Google Scholar]

[4] Uddin M N, Mashud O M, Waliullah T, et al. Effect of Introducing Large Scale Roughness through Static Curvature Modifications on the Low Speed Flow over an Airfoil[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, 2013 [Google Scholar]

[5] Wannan W, Qinglin S, Mingwei S, et al. Modeling and Control of Parafoil Based on Computational Fluid Dynamics[J]. Applied Mathematical Modelling, 2019(70): 378–401 [Article] (in Chinese) [Google Scholar]

[6] Tao J, Liang W, Sun Q L, et al. Modeling and Control of a Powered Parafoil in Wind and Rain Environments[J]. IEEE Trans on Aerospace and Electronic Systems, 2017, 53(4): 1642–1659 [Article] [CrossRef] [Google Scholar]

[7] Ghoreyshi M, Bergeron K, Lofthouse A J, et al. CFD Calculation of Stability and Control Derivatives for Ram-Air Parachutes[C]//AIAA Atmospheric Flight Mechanics Conference, 2016 [Google Scholar]

[8] Tao J, Sun Q L, Liang W, et al. Computational Fluid Dynamics Based Dynamic Modeling of Parafoil System[J]. Applied Mathematical Modelling, 2018(54): 136–150 [Article] (in Chinese) [CrossRef] [Google Scholar]

[9] Fogell N, Sherwin S J, Cotter C J, et al. Fluid-Structure Interaction Simulation of the Inflated Shape of Ram-Air Parachutes[C]//27th AIAA Aerodynamic Decelerator Systems Conference, 2013 [Google Scholar]

[10] Peralta R, Johari H. Geometry of a Ram-Air Parachute Canopy in Steady Flight from Numerical Simulations[C]//23rd AIAA Aerodynamic Decelerator Systems Technology Conference, 2015 [Google Scholar]

[11] Zhang Siyu, Yu Li, Liu Xing. Numerical Simulation of Parafoil Inflation Process Based on Fluid-Structure Interaction Method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(6): 1108–1115 [Article] (in Chinese) [Google Scholar]

[12] Zhang Chun, Cao Yihua. Numerical Simulation of Parafoil Aerodynamics and Structural Deformation Based on Loose Coupled Method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 605–609 [Article] (in Chinese) [Google Scholar]

[13] Slegers N, Costello M. Aspects of Control for a Parafoil and Payload System[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(6): 898–905 [Article] [CrossRef] [Google Scholar]

[14] Sun Qinglin, Liang Wei, Tao Jin, et al. Dynamic Modeling of Parafoil Based on CFD Simulation and Least Square[J]. Trans of Beijing Institute of Technology, 2017, 37(2): 157–162 [Article] (in Chinese) [Google Scholar]

[15] Longfang W, Weiliang M. Analytical Study on Deformation and Structural Safety of Parafoil[J]. International Journal of Aerospace Engineering, 2018, 16: 1–7 [Article] (in Chinese) [Google Scholar]

[16] Omprakash N A. Modeling and Simulation of 9-DOF Parafoil-Payload System Flight Dynamics[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2006 [Google Scholar]

[17] Liu Yuan, Yan Jianguo, Li Mingjun, et al. Research on Aerodynamic Performance of Ram-Air Parafoil[J]. Flight Dynamics, 2017, 35(3): 24–27 [Article] (in Chinese) [Google Scholar]