| Issue |
JNWPU
Volume 41, Number 1, February 2023
|
|
|---|---|---|
| Page(s) | 180 - 187 | |
| DOI | https://doi.org/10.1051/jnwpu/20234110180 | |
| Published online | 02 June 2023 | |
A calculation method of soft soil pressure bearing mathematical model under repeated load
重复载荷下软土承压模型的计算方法研究
School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China
Received:
15
April
2022
The soft soil pressure bearing mathematical model under repeated normal load is established and its program is implemented. The relationship of soft soil between pressure and settlement under repeated load is solved. Taking the settlement volume, contact area and loading times as independent variables and soil deformation force as dependent variables, the calculus equation of soil deformation force at the arbitrary position is deduced. The soil is discretized section by section in the settlement direction, and the bearing coefficient of the corresponding section is applied. During the unloading-loading period, the calculation formulas of the corresponding stable point and the stiffness of the soil rebounding line are given, and the load settlement program of soft soil is compiled. The soil stiffness value is substituted into the calculus equation, and the Adams software is redeveloped with C/C++language to obtain the load settlement curve. On the soft soil terrain, three kinds of flat plates with diameters of 6, 8, and 10 cm are used to carry out the pressure penetration test to obtain the corresponding pressure-settlement curve. The error between the simulation and experimental results of the mathematical model is no more than 10%.
摘要
对重复法向载荷下的软土承压模型进行数学建模及程序实现, 求解重复加载下软土的压力沉陷关系。以沉陷量、接触面积及加载次数为自变量, 土壤变形力为因变量, 推导任意位置土壤变形力的微积分方程。沿沉陷方向将土壤分段离散, 施加对应分段的分段承载系数, 并在卸载-加载期间, 给出对应的稳定点计算公式和土壤反弹线刚度, 编制松软土壤的载荷沉陷程序。将土壤刚度值代入微积分方程, 利用C/C++语言对Adams进行二次开发, 获得载荷沉陷曲线。在软土地形上, 利用直径为6, 8, 10 cm的3种平板, 实施压板贯入试验获得对应的压力-沉陷曲线, 模型的仿真与试验结果误差不超过10%。
Key words: repeated load / calculation model / mathematical modeling / load-settlement curve / soil settlement
关键字 : 重复加载 / 计算模型 / 数学建模 / 载荷-沉陷曲线 / 土壤沉陷
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
星球车在火星或月球表面运动, 地表土壤受压沉陷。若外加载荷减小, 土壤高度会出现微小反弹。当星球车直线行驶时, 多轮依次碾压同一土壤, 随外加负载变化, 土壤高度会出现连续改变。试验表明土壤在多次受压沉陷过程的压力沉陷行为相同[1]。
目前, 星球车移动系统常用结构为六轮驱动主副摇臂悬架结构。若不发生侧倾, 两侧悬架承受相同力和力矩。受车体步态调整及悬架自身结构影响[2], 同一侧悬架的前后驱动轮承重不同。此外, 星球表面存在大量岩石导致星球车刚轮表面出现破损[3]。因此, 轮下土壤会在不同负载下因重复碾压而出现不同深度沉陷。火星及月球表面土壤十分松软, 车轮的重复碾压易造成土壤沉陷量不断增大, 最终成为静观测平台。为延长车体使用寿命, 星球车运动速度一般较低, 毅力号火星车最大速度约为240 m/h, 祝融号火星车运动速度约为40 m/h。
通过对Apollo14~16, 20号探测器所携带月壤样本的分析, Carrier团队[4]以及郑永春团队[5]获得月壤孔隙比及其最大最小值。根据月壤孔隙比, 哈尔滨工业大学丁亮[6]得到月壤相对密实度为0.856, 0.707, 0.608, 0.669, 据此提出车轮碾压后的土壤仍存在一定的反弹变形能力。Wong和Reece[7]提出土壤反弹发生在轮壤相互作用的离去角区域, 并给出相应离去角区域的土壤力和力矩计算公式。
载荷-沉陷模型是分析重复加载下软土压力沉陷关系的基础。自Bernstain提出沉陷量与接地载荷的近似简化表达式, Bekker[8]总结莱多石涅夫引入土壤抗变形强度系数以及土木工程中微小下陷量与压力呈线性关系的成果, 提出适合越野车辆的经典载荷沉陷公式, 之后又提出重复加载下的压力沉陷公式, 但该公式不能体现沉陷的累加性。通过对车轮在同一地形进行多次碾压试验, Holm[9]提出车轮碾压后地形特性会发生改变, 且地形变化与车轮滑移有关, 但Holm模型参数计算复杂, 不易展开仿真建模分析。黄祖永[10]提出软土的重复加载沉陷模型, 其中, 卸载和重新加载阶段的压力沉陷关系近似为一条直线的结论已被众多学者认同[11-12]。但该模型沿接触面的法向应力是不严格遵循下沉单调趋势的分段函数, 因此, Wong模型求解困难[13]。若能对Wong的重复加载模型分析, 提出适合于机器语言的计算模型, 则可以将其应用于求解车轮多次碾压同一土壤的沉陷问题。
本文提出一种基于Wong重复加载下求解软土承压模型的计算方法, 将Wong模型进行数学建模, 编制算法程序。其中考虑了: ①多次加载后地形点位置变化; ②随土壤深度增加, 其承载能力增加; ③卸载后的土壤会产生微小反弹等3种情况, 进而推导出描述重复加载下软土任意位置点承压特性的微积分模型。该模型反映了随加载次序和载荷大小变化, 地形高度和沿土壤沉陷方向的力学特性发生改变的现象。将该计算模型编制成仿真程序, 以3组不同直径的平板实施载荷沉陷仿真和压板试验, 验证建模方法的有效性。
1 载荷沉陷模型研究
1.1 Bekker承压模型
无限大均质软土地形上, 对平板施加法向载荷, 平板下方土壤发生下陷。土壤沉陷量与其承压特性及外加载荷有关。如图1所示, W为所施加的外加法向载荷, r为平板的曲率半径, z为沉陷量, p为对应产生的土壤压力。
针对无限大的均质土壤, Bekker承压模型[8]
式中:kc为土壤黏聚变形模量, N/cmn+1;kϕ为土壤摩擦变形模量, N/cmn+2;n为土壤变形指数;p为平板上的法向压力, N/cm2, z为沉陷量, cm。
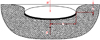 |
图1 土壤压力沉陷示意图 |
1.2 重复性法向加载响应
星球车一般为多轮轴形式, 车体下方土壤微元经前轮碾压后, 土壤会发生沉陷。若后续车轮在该微元上进行再次碾压, 载荷会重新施加其上。多轮通过时, 该土壤微元会循环经历加载-卸载-再加载的过程。
Bekker给出车辆重复经过摩擦性土壤时, 车轮沉陷的最大深度。假设车辆载荷pi递增, 对于经过同一车辙的每个低压充气轮胎和履带的实际沉陷可以近似表示为
式中,i为加载序号。当i=1时, zi-1为0, z′1= , 车辙的最大深度为
, 车辙的最大深度为
但Bekker理论不能表示重复加载时沉陷量累加的现象。根据重复加载后压力沉陷试验结果, Wong认为软土在卸载和重新加载过程中, 压力沉陷关系可以近似为一条直线, 如图2所示。
图2中, 土壤承受连续不间断的载荷时, 压力沉陷关系可以由1.1节中的Bekker承压公式来近似描述, 即
对于卸载-再加载过程, 压力沉陷关系可以采用公式(5)描述[10]
式中:pv和zv分别是卸载开始时的压力和下沉量; kv是回弹刚度, 表示卸载-再加载过程, 即土壤反弹线的平均斜率。kv是zv的函数, 其关系可以描述为
式中,u和c为土壤参数, 两者数值均为定值, 由试验得到。Wong测得试验土壤为沙子时的土壤参数u为0, c为50 300 kN/m4。
2 计算模型
求解重复加载下软土受压沉陷的实际问题时, Wong模型从理论角度分析了压力沉陷关系, 但用于计算时, 由于Wong模型是一个不严格遵循下沉单调的分段曲线, 因此需要对模型进行适应性修正, 以获得适合求解的计算模型。模型修正包括2个方面: ①将连续加载段进行分段, 分段提供承载力; ②提出新的卸载-再加载段的土壤刚度计算公式。
通过分析Bekker、Wong的载荷沉陷模型及其重复加载沉陷模型, 推导出重复法向载荷下土壤沉陷的计算模型。
推导过程如下:
在无限大的塑型均质土壤上, 有:
假设若第i+1次加载载荷小于等于第i次载荷, 且将其重复作用于同一土壤微元时, 不会对沉陷量产生影响。
在重复载荷作用下, 面积为A的平板在软土上发生z′大小的沉陷。对面积A进行微分, 每个微小土壤单元的面积为ΔA, 同时对沉陷量z′微分, 每一小段的沉陷量为Δz′。
对于平板下第j(j=1, 2, 3, …)个面积为ΔA的土壤单元进行分析:
第i(i=1, 2, 3, …)个Δz′处的土壤压力为
式中, pi-1为第i-1个Δz′处的土壤压力, 且p0=0, k′为土壤承压参数, k′=kc/b+kϕ, ki为分段承载系数。相同土壤条件下, 分段承载系数ki主要受沉陷量影响, 其值可以由压板试验获得。令分段承载曲线刚度k′i=ki·k′, 如图3所示。
对于第j个土壤单元, 由于重复加载, 导致地形高度不断降低。若第(m-1)次加载后的地形高度为hm-1·Δz(h=0, 1, 2, 3…), 且h0=0, 则第m(m=1, 2, 3, …)次加载时, 第i个Δz′的土壤压力为
那么, 面积为A′的土壤在沉陷量为z′处对m次加载后的平板所施加的作用力为
式中, z′=(i-1)Δz′+z, ΔAi=dA。由于式中pi-1为常数, 因此有
对于沉陷量z的计算, 地形初始点z0m为
式中: z′max为(m-1)次加载时土壤沉陷的最大高度; (Wmax-mplateg)/ku为第(m-1)次土壤反弹高度; mplate为压板质量。
Wong的重复加载模型在程序计算时比较复杂, 其原因为: 地形表面的所有位置点需要储存其变形信息, 包括u和c等土壤参数, 才能计算回弹刚度kv。鉴于此, 通过对试验数据分析, 卸载-再加载段的土壤反弹线刚度kv可以由(12)式计算
式中, km-1, zm-1为第(m-1)次加载后, 卸载起始时的所在分段土壤刚度和总沉陷量, a为土壤修正参数, 由试验和仿真拟合确定。(12)式与(6)式虽然在形式上相似, 但具体参数含义完全不同。(12)式的参数是与卸载开始时的沉陷和所在承载段的斜率有关的变量, 程序可以自动调用初始输入对应分段的刚度值。而(6)式中的参数是完全由试验得到的计算值, u和c是与卸载点斜率无关的定值。
图4中, zi, pi, ki分别为对应分段i上土壤沉陷位置、土壤压力以及土壤刚度。加载过程为: 当法向载荷第一次加载于压板上, 压板下方土壤的压力沉陷关系沿分段承载曲线o-a-c变化。假设当压板稳定时, 压板下方土壤位于c点处。此时撤去压板上的外加法向载荷, 土壤位置沿线段c-d上升。由于压板自身重力的存在, 土壤位置最终会停在k点, 土壤反弹高度为kk′, 若压板自身质量被逐渐平衡, 直到压板被撤去, 压板下方土壤将沿kd线反弹至d处。此时, 土壤的沉陷量为z′2, 土壤反弹高度为dh。当压板在原位置再次加载, 压板下方土壤的压力沉陷关系沿线段dd′变化, 直到d′点处, 土壤刚度由kv变成k2。若再次加载, 压板下方土壤的压力沉陷关系继续沿相应分段曲线进行变化。
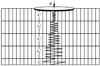 |
图3 土壤分段刚度模型示意图 |
 |
图4 重复加载压板的载荷-沉陷曲线 |
3 模型程序实现
3.1 程序说明
为了程序便于后续使用, 需对其中的重要部分进行适当说明。
1) 当对同一土壤微元进行重复加载时, 需要区分第i次和第(i+1)次加载的分界点。此处规定: 不计土壤承载力, 若对土壤施加的合外力的法向分力大小或方向发生变化, 则认为第i次加载结束, 第(i+1)加载开始。
2) 产生新的土壤反弹线需要具备2个条件: ①土壤沉陷点在分段承载曲线上; ②第(i+1)次加载载荷大于前i次加载载荷的最大值。
3) 若土壤因卸载进入土壤反弹线, 需要施加大于卸载点处载荷的外加载荷才能保证土壤重新进入分段承载曲线。
4) 土壤承载力计算与加载顺序、外加载荷大小方向存在直接关系, 两者会影响土壤承载力进入加载阶段或者卸载-再加载阶段。
3.2 程序结构分析
图5为程序总体流程图, 描述了程序求解研究对象(压板或者车轮)在受载过程中的土壤承载力计算过程。
由图5可知, 判断受载土壤位置决定土壤承载力由土壤分段承载曲线对应函数或土壤反弹线对应函数计算。
如图6所示, F为对土壤施加的第i次外加载荷, Fyuan为第(i-1)次外加载荷, Fmax为前(i-1)次施加的载荷中的最大值, P为受载土壤位置, Pf1为卸载点位置, Pf2为土壤稳定点位置。图中,“==”表示判断符号两侧数值是否相等;“=”表示右侧数值向左侧变量赋值;“!=”判断符号两侧数值是否不相等;“≤”“≥”分别表示数学上的小于等于及大于等于含义。
根据flag9, flag10, flag11等参数值的交叉组合, 获得土壤承载力的计算公式。其中:
1) 若flag9为2, 则存在土壤反弹曲线, 之后土壤承载力计算均在土壤反弹曲线上, 直到有新的外加载荷出现, 使其跳出土壤反弹曲线。
2) 若flag9为1, flag11为2, P<Pf2, 则土壤承载力为0, 此时, 悬空。
3) 若flag9为1, flag11为2, P>Pf1, 则土壤承载力计算在土壤分段承载曲线上。
4) 若flag9为1, flag11为2, Pf2≤P≤Pf1, 则土壤承载力计算在土壤反弹曲线上。
5) 若flag9为1, flag11为1, 则土壤承载力计算在分段承载曲线上。
 |
图5 程序总体流程图 |
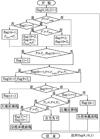 |
图6 判断土壤位置程序流程图 |
相关参数含义
4 压板试验
4.1 压板仿真
在Adams中建立压板虚拟模型, 并在压板质心处添加GFORCE单元[14-16], 以模拟压板-土壤相互作用时产生的土壤支持力。在动力学软件Adams中, 对GFORCE单元进行二次开发, 将图5仿真程序代入开发的GFOSUB子程序中, 在对应工况下进行压板贯入试验。
仿真条件: 试验中所采用的土壤为沙壤, 因此模型中使用的相关参数为与沙壤的相关参数。对直径为10 cm的压板做试验, 绘制载荷-沉陷图, 对数据点进行拟合, 获得拟合曲线。对拟合曲线分段, 求解对应节点上的分段承载系数, 拟合曲线图如图7所示。
将图7中的拟合点数据代入(13)式中, 获得分段承载系数ki, ki=1 N/cm, (i=1, 2, 3, …)。
式中:W为载荷值;A为压板面积;k′为土壤承压参数;Δz为分段长度, 相关参数设置如表2所示。
仿真中使用的压板直径为6, 8, 10 cm, 压板质量为0.21 kg。根据《地面-车辆系统导论》及《地面车辆原理》, 本文压板直径的选取考虑了2个方面: ①与所研究星球车车轮宽度接近, Bekker指出压板直径与车轮尺寸越接近, 对轮壤接触的模拟效果越好; ②2组及以上数量压板试验基本可说明土壤的承压性能。通过对试验数据进行多次拟合分析, 得到卸载-再加载段的土壤修正系数a为200 N/cm。
 |
图7 压板载荷沉陷图 |
土壤力学参数
4.2 压板试验
为验证模型和程序的有效性, 需要做重复加载下的压板试验。图8为压板装置示意图, 压板试验装置由配重1, 压力传感器2, 固定环3, 拉绳传感器4, 压杆5, 压板6, 土槽7, 固定台8, 加载台9, 龙门架10, 步进电机11, 滚珠丝杆12, 提升杆13组成。试验用软土采用干沙, 因其物理性质最接近火星土壤。干沙的沙粒直径小于2 mm, 土槽内干沙厚度为40 cm。加载台上放置配重块, 通过压杆对其下方压板施加恒定压力。拉绳传感器固定在固定台上, 由绳线获取压板沉陷量, 并通过压力传感器获得对应沉陷位置处压杆的压力值。
压板试验装置实物图如图9所示。
试验用压力传感器的型号为PSD-S1,精度为0.001 kg,适用范围为0~100 kg;位移传感器的型号为MPS拉绳传感器,精度为0.01 mm,适用范围为0~100 mm;步进电机型号为J-5718HB6401;滚珠丝杆为GX80,精度为0.03 mm,适用范围为0.01~100 mm。
加载过程为: 对压板进行加载, 待压板稳定, 记录沉陷高度; 继续加载, 待压板稳定, 记录沉陷高度; 逐渐撤去压板上配重, 直到配重为零, 记录此卸载过程中的沉陷量及对应负载。此时, 缓慢加载, 直到重新到达卸载位置, 记录再加载过程的沉陷量和负载变化。重复上述过程, 最后将对应载荷和沉陷位置按加载顺序排列, 获得载荷-沉陷图像。
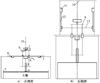 |
图8 压板试验装置 |
 |
图9 压板试验装置 |
4.3 结果及讨论
通过动力学软件MSC.Adams和压板试验装置对直径为10, 8, 6 cm的压板分别进行仿真和试验, 获得如图10~12所示的3种压板的载荷-沉陷图像。虚线为仿真得到的加载段数据, 由分段承载曲线表示, 点划线为仿真得到的卸载-再加载段数据, 由土壤反弹曲线表示, 星号表示试验得到的持续加载段数据, 小圆圈表示试验得到的卸载-再加载段数据。压板试验和仿真的沉陷量范围为0~4 cm, 该范围为星球车正常运行时常用的沉陷量范围。通过分析图10~12, 可以得到如下结论:
1) 为了说明三图中加载段沉陷量与载荷点对应仿真值和试验值的相符性, 采用相对误差概念描述两者的误差大小:
式中: η为相对误差; a为理论值; b为实际值。
对于直径为10 cm平板, 相对误差η≤6%, 对于直径为8 cm平板, 相对误差η≤9%, 对于直径为6 cm平板, 相对误差η≤8%。分段承载系数是由直径10 cm的平板得到, 因此, 数据的拟合结果比直径为8 cm和6 cm的平板更好。相对误差在10%以内, 说明分段承载曲线具有一定的有效性。
2) 卸载-再加载段的仿真和试验结果的相对误差小于10%, 说明土壤在卸载-再加载段的刚度与卸载点的刚度和沉陷量具有一定关系。该结论与Wong模型中(6)式以及Holm模型得出的结果相似, 验证了所提出模型的有效性。
3) 对比仿真和试验中分段承载曲线和卸载-再加载曲线的斜率时, 可以得到: 卸载-再加载段的土壤刚度比土壤承受连续加载时的土壤刚度要大。这是由于土壤本身的塑性特性造成了卸载-再加载的土壤反弹阶段, 土壤高度变化很小。这也进一步说明了土壤具有塑性和弹性性质, 但塑性性质占主要部分。这一现象与丁亮博士使用月壤的相对密实度得到的结论一致, 虽然土壤存在一定的反弹能力, 但反弹量很小。因此即使完全卸载, 土壤微元也不会重新回到起始点, 产生的沉陷量也不会完全消失。
4) 由图10~12对比可知, 直径10 cm的分段曲线斜率>直径8 cm的分段曲线斜率>直径6 cm的分段曲线斜率, 这意味着土壤载荷是与压板和土壤的有效接触面积有关。
 |
图10 直径10 cm平板 |
 |
图11 直径8 cm平板 |
 |
图12 直径6 cm平板 |
5 结论
针对于同一软土土壤重复加载的压力沉陷求解问题, 使用Wong的重复加载模型作为理论模型, 获得如下结论:
1) 针对于Wong重复加载模型的应用问题, 即接触面压力的求解是一个不严格遵循单调的分段函数, 分析了土壤受载下陷过程中压力沉陷量的变化。
2) 提出了一种适用于求解车轮多次碾压同一土壤等土壤重复加载问题的计算模型, 沿土壤深度方向分段, 给对应分段施加分段刚度系数, 提出卸载-再加载过程中土壤反弹线的修正公式。对Wong重复加载模型重新进行数学建模, 并将获得的计算模型编制成可以供用户调用的仿真程序。
3) 将该程序用于压板试验中, 对比压板试验和仿真的结果验证模型及程序的正确性, 验证结果显示,压板仿真与试验误差不超过10%。
References
- WONG J Y, GARBER M, PRESTON-THOMAS J. Theoretical prediction and experimental substantiation of the ground pressure distribution and tractive performance of tracked vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Transport Engineering, 1984, 198(4): 265–285. [Article] [CrossRef] [Google Scholar]
- ZHENG Junqiang. Research on wheel-step mobile system and wriggling crawl strategy of a six wheeled rocker type mars rover[D]. Harbin: Harbin Institute of Technology, 2019 (in Chinese) [Google Scholar]
- PAN Dong, JIA Yang, YUAN Baofeng, et al. Design and verification of the active suspension mobility system of the the Zhurong Mars rover[J]. Scientia Sinca Technologica, 2022, 52: 278–291. [Article] (in Chinese) [CrossRef] [Google Scholar]
- HEIKEN G H, VANIMAN D T, FRENCH B M. Lunar sourcebook: a user's guide to the moon[M]. London: Cambridge University Press, 1991: 475–567 [Google Scholar]
- ZHENG Yongchun, OUYANG Ziyuan, WANG Shijie, et al. Physical and mechanical properties of punar pegolith[J]. Mineralogy and Petrology, 2004(4): 14–19. [Article] (in Chinese) [Google Scholar]
- DING Liang. Wheel-soil interaction terramechanics for lunar/planetary exploration rovers: modeling and application[D]. Harbin: Harbin Institute of Technology, 2010 (in Chinese) [Google Scholar]
- WONG J, REECE A R. Prediction of rigid wheel performance based on the analysis of soil-wheel stresses. Part Ⅱ: performance of towed rigid wheels[J]. Journal of Terramechanics, 1967, 4(2): 7–25. [Article] [Google Scholar]
- BEKKER M G. Introduction to terrain-vehicle systems. Part Ⅰ: the terrain[D]. Ann Arbor: Universtity of Michigan, 1969 [Google Scholar]
- HOLM I C. Multi-pass behaviour of pneumatic tires[J]. Journal of Terramechanics, 1969, 6(3): 47–71. [Article] [CrossRef] [Google Scholar]
- WONG Joyung. Theory of ground vehicles[M]. 4th ed. Beijing: China Machine Press, 2018 (in Chinese) [Google Scholar]
- HE R, SANDU C, MOUSAVI H, et al. Updated standards of the international society for terrain-vehicle systems[J]. Journal of Terramechanics, 2020, 91: 185–231. [Article] [Google Scholar]
- SALMAN N D, KISS P. A study of pressure-sinkage relationship used in a tyre-terrain interaction[J]. International Journal of Engineering and Management Sciences, 2019, 4(1): 186–199. [Article] [Google Scholar]
- SENATORE C, SANDU C. Off-road tire modeling and the multi-pass effect for vehicle dynamics simulation[J]. Journal of Terramechanics, 2011, 48(4): 265–276. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- AZIMI A. Wheel-soil interaction modelling for rover simulation and analysis[D]. Montreal: McGill University, 2014 [Google Scholar]
- GHOTBI B, GONZÁLEZ F, KÖVECSES J, et al. Mobility evaluation of wheeled robots on soft terrain: effect of internal force distribution[J]. Mechanism and Machine Theory, 2016, 100: 259–282. [Article] [CrossRef] [Google Scholar]
- ZHANG Bowen, TENG Baoyi, HUANG Tieqiu. Design and research co-simulation platform of navigation and dynamics on planetary rovers[J]. Journal of Northwestern Polytechnical University, 2019, 37(6): 1184–1190. [Article] (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 土壤压力沉陷示意图 |
| In the text | |
 |
图2 软土对重复法向载荷的响应曲线[10] |
| In the text | |
 |
图3 土壤分段刚度模型示意图 |
| In the text | |
 |
图4 重复加载压板的载荷-沉陷曲线 |
| In the text | |
 |
图5 程序总体流程图 |
| In the text | |
 |
图6 判断土壤位置程序流程图 |
| In the text | |
 |
图7 压板载荷沉陷图 |
| In the text | |
 |
图8 压板试验装置 |
| In the text | |
 |
图9 压板试验装置 |
| In the text | |
 |
图10 直径10 cm平板 |
| In the text | |
 |
图11 直径8 cm平板 |
| In the text | |
 |
图12 直径6 cm平板 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


