| Issue |
JNWPU
Volume 41, Number 5, Octobre 2023
|
|
|---|---|---|
| Page(s) | 932 - 941 | |
| DOI | https://doi.org/10.1051/jnwpu/20234150932 | |
| Published online | 11 December 2023 | |
A fatigue crack quantification model for metallic structure based on strain monitoring data
基于应变监控数据的金属结构疲劳裂纹量化模型研究
1
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China
2
Department of Strength Design, AVIC the First Aircraft Institute, Xi'an 710089, China
3
School of Aeronautic Engineering, Air Force Engineering University, Xi'an 710038, China
Received:
14
October
2022
Obtaining the real-time fatigue crack length of a metallic structure is the prerequisite of the fatigue life monitoring and residual life estimation for an aircraft. This paper proposed a metallic structure's fatigue crack prediction model using strain monitoring data based on deep learning method. A cycle consistent adversarial network was developed to map the strain monitoring data from experimental measurement with those from finite element modeling. A crack size classification model and a crack length quantification model were proposed to classify the crack size range and identify the exact crack length, respectively. The proposed model was applied to predict the fatigue crack growth in centeral hole metallic plates subjected to random loading spectrum. The results showed that the prediction is effective and accurate.
摘要
实时获取金属结构的疲劳裂纹长度是开展飞机单机寿命监控和剩余寿命估算的基础。采用深度学习方法, 提出了一种基于应变监控数据的金属结构疲劳裂纹长度预测模型, 通过构造循环对抗网络模型、裂纹尺寸的分类模型和裂纹长度的量化模型, 分别实现了含裂纹结构的应变试验数据与有限元模型数据的映射、裂纹尺寸范围的准确分类、裂纹长度的精确量化。将上述方法应用于中心带孔金属板在随机载荷谱下的疲劳裂纹监测, 有效实现了疲劳裂纹长度的实时预测。与试验结果对比表明, 单孔板的孔边疲劳裂纹长度预测误差小于1 mm, 满足工程实际的需求。
Key words: fatigue crack / strain monitoring / deep learning / data driven model / fatigue crack prediction
关键字 : 疲劳裂纹 / 应变监测 / 深度学习 / 数据驱动模型 / 疲劳裂纹预测
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
近年来, 先进飞行器的研制和制造成本急速攀升, 对飞行器结构的耐久性、可靠性、经济性等提出了挑战[1]。掌握飞行器结构在服役过程中的损伤数据, 是开展飞行器结构健康状态评估的基础, 也是实施其寿命消耗计算、检修维护时机确定、延寿等寿命工作的基础[2-3]。
基于物理模型的结构寿命预测方法被广泛用于飞机结构寿命评定工作, 尤其是损伤容限设计思想指导下的结构扩展寿命评定时, 主要采用断裂力学相关方法工具, 通过求解结构裂纹尖端应力强度因子, 并结合裂纹扩展速率公式, 可实现结构裂纹扩展过程的预测。经典的裂纹扩展速率公式包括Paris公式[4]、Walker公式[5]、Forman公式[6]等, 在工程实际上得到了广泛应用。
采用裂纹传感器直接获取结构服役过程中的疲劳裂纹信息, 是目前实现结构健康监控的重要手段。按照是否可以在服役过程中实时得到裂纹信息, 可分为在线检测方法与离线检测方法[7]。在线检测方法是指通过永久布置在结构上的传感器网络, 实现对结构状态的实时、连续、长期评估[8], 是未来飞行器实现自感知、自诊断等智能化发展的主要方向[9]。
目前常用的裂纹长度在线检测技术有: 主动Lamb波方法、涡流阵列传感器检测法、压电阻抗法、光纤传感器检测法等[10]。主动Lamb波在结构中被激励时, 随着裂纹扩展, Lamb波响应信号会发生变化, 通过分析响应信号与裂纹尺寸的规律, 可实现复杂结构的裂纹长度与位置的检测[10]; 涡流阵列传感器由一个或多个感应线圈构成, 对涡流检测输出信号进行分析, 得出裂纹长度信息; 压电阻抗法通过检测传感器在工作环境下的电阻抗性而推断结构裂纹扩展情况[11]; 光纤传感器的反射光会随着外界应力梯度的变化而变化, 通过测量应力场的变化, 进而推断结构裂纹信息。上述裂纹在线监测方法为先进飞行器的服役与维护提供了很好的基础, 但其拓展至工程应用时还面临较多困难, 主要原因是新式传感器的可靠性、使用寿命、轻量化、空地一致性等还需要进行大量工程验证。设计一种精度高、响应快、成本低的结构疲劳裂纹在线检测方法, 对飞机结构健康监控技术的发展具有重要意义[12]。
结构应变的飞行采集, 是当前飞机飞行测试技术中较成熟的测试手段, 通过在结构表面粘贴应变计(如电阻式应变片、光纤光栅传感器等), 获得飞机在飞行过程中结构表面应变的实时变化, 进而获得载荷变化历程, 计算得到结构疲劳损伤的累积和寿命消耗量。因此, 实时采集的应变数据常被用于单机寿命监控。
当结构出现裂纹时, 结构刚度、载荷传递路径等会发生改变, 使得结构某些位置的局部应变值发生显著变化。基于该原理, 有学者尝试将结构表面应变值与其裂纹特征建立关联, 进而根据实测采集的应变值推断出裂纹的长度、方向、形式等信息。Deans等[13]建立了紧凑拉伸试件裂纹长度与试件背面应变和试件载荷之间关系, 进而从载荷与应变测量结果推断出裂纹长度。Crocombe等[14]建立了粘接结构背侧应变与损伤之间的关系, 进而通过应变实测数据推断出粘接结构疲劳损伤演化。这种方法较方便、简易, 可准确得到结构损伤信息, 但对于几何形式较复杂的结构, 裂纹长度与应变、载荷之间关系较难建立, 可能并非一一映射关系, 且应变测量位置如何确定成为主要难点。Newman等[15]进一步考虑紧凑拉伸试件的厚度, 并且引入更多的非线性参数拟合裂纹长度与试件背面应变、载荷之间关系, 精度进一步提高, 但没有提出如何解决其他类型试件裂纹长度预测的应变测量位置问题, 并且拟合方程只适用紧凑拉伸试件, 无法做进一步推广。
机器学习方法近年来被广泛用于结构寿命研究[16-18], 该方法可准确建立输入、输出数据之间的非线性关系。庞杰[19]提出了基于机器学习的裂纹识别方法,实现了裂纹长度、位置、形状等信息的准确预测。王珲玮[20]使用BP(back propagation)神经网络对导弹模型的飞行载荷进行识别, 使用速度、高度、迎角等飞行参数作为输入, 输出关键截面的载荷。Trivailo等[21]使用神经网络对飞机尾翼的疲劳载荷进行预测, 利用应变片获取的应变值预测尾翼的载荷。郑星等[22]采用分段线性回归方法实现了基于实测应变数据的结构疲劳裂纹检测, 取得了较准确的结果。
综上所述, 传统的基于物理模型裂纹预测方法容易受到结构服役过程与试验过程之间不一致性的影响, 而现有的裂纹传感器在工程实用上尚有差距。本文提出一种基于应变监控数据的疲劳裂纹深度学习实时预测方法, 将实时采集的应变数据输入建立的裂纹量化模型中, 可得到当前裂纹长度, 该方法解决了因试验与服役偏差带来的裂纹长度预测不准确的问题, 为飞机的检修与维护、寿命管理、寿命监控等提供理论依据。
1 基于应变监控数据的结构疲劳裂纹量化模型
1.1 方法原理
本文提出了一种结构疲劳裂纹量化模型方法。建立测点应变与裂纹长度的关系, 通过实时采集应变数据, 输入模型中, 得到裂纹长度的预测值。该方法建立试验数据与有限元模拟数据之间的映射, 从而减小试验数据与有限元模拟数据之间因试验过程、试验设备、有限元建模等因素导致的偏差; 将结构裂纹尺寸分类, 不同尺寸的裂纹分别建立裂纹量化模型, 提高裂纹长度的预测精度。
该模型建立方法流程如图 1所示, 涉及4个主要内容: 确定应变监控部位、建立循环生成对抗网络[23](cycle-consistent adversarial networks, CycleGAN)、建立裂纹尺寸的分类模型(classifying model, CM)、建立裂纹长度的量化模型(quantifying model, QM)。
通过建立含裂纹结构的有限元分析(finite element analysis, FEA)模型, 采用1.2节方法确定出应变监控部位, 依据计算结果获得监控部位的有限元分析应变数据(finite element analysis strain data, FSD)。进入训练步, 用FSD训练CycleGAN、CM、QM模型, 判断3个模型的精度是否满足要求, 当不满足要求时重新选择应变监控部位, 直到满足精度要求, 结束训练步。进入预测步, 首先通过CycleGAN将试验数据映射为“假”FSD数据(fake finite element analysis strain data, Fake-FSD)输入到CM中得到裂纹尺寸范围的预测, 再将Fake-FSD输入到符合裂纹尺寸范围预测的裂纹长度量化子模型(quantifying sub-model, sub-QM)中, 得到裂纹长度的量化预测。判断量化预测是否达到可接受的精度要求, 若没有, 则需重新选择应变监控部位后进入训练步, 若可接受, 则结束模型的训练。训练完成的模型可用于实时裂纹预测, 将实时采集的监控点应变数据经过预测步输入模型得到当前裂纹长度的预测。
上述3类机器学习模型的主要作用为:
1) CycleGAN模型建立试验数据与FSD之间的映射关系。由于试验与FEA计算过程不可避免地存在偏差, 为增加裂纹预测模型的准确性, 将试验实测的应变数据输入CycleGAN的生成器(generator), 得到与FSD相似的Fake-FSD, 实现FSD与试验数据的映射, 减小试验数据与FSD差异对模型精度的影响。
2) CM模型基于人工神经网络(artificial neural network, ANN), 用于对结构裂纹的尺寸进行分类。模型输入为经过1.2节方法处理后的Fake-FSD, 输出为裂纹尺寸范围的判断, 当裂纹尺寸较短时应变值对裂纹长度的变化不敏感, 为增强短裂纹预测能力, 需要减少长裂纹应变数据干扰。根据裂纹扩展范围设置阈值并划分裂纹尺寸范围, 通过CM模型对裂纹尺寸分类。
3) QM模型基于ANN, 用于预测结构裂纹长度。模型输入为经过1.2节方法处理后的Fake-FSD, 输出为裂纹量化预测, QM含有多个用于裂纹长度量化的sub-QM, 根据建立CM过程中裂纹扩展范围设置的阈值, 可分别建立用于预测不同尺寸范围的sub-QM, 将CycleGAN得到的Fake-FSD代入符合CM裂纹尺寸范围判断的sub-QM中, 得到裂纹长度量化的预测值。
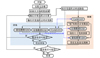 |
图1 基于应变监控数据的结构疲劳裂纹量化模型方法流程图 |
1.2 数值分析数据的预处理方法
机器学习模型的建立依赖于大量的数据, 若仅依靠试验获得这些数据, 其成本无法接受。随着数值模拟方法的不断完善, 采用FEA可实现结构疲劳裂纹扩展的高保真计算。通过建立FEA模型可快速获得大量与试验结果相似的模拟数据, 大大降低成本。为获得大量的用于机器学习模型训练数据, 可建立待预测结构的FEA模型, 通过更改FEA模型裂纹长度、位置、方向等变量, 形成用于训练的数据源。
根据结构形式和受载特点, 判断可能出现的裂纹具有的形式及位置特点, 推断裂纹可扩展范围。假设某条裂纹长度范围ai ~ aj, 步长d=Δa, 则该裂纹可能出现的长度有n种, n=|aj-ai|/Δa; 若结构上可能有m条裂纹, 且每条裂纹的变量个数相同, 则共需要建立nm个FEA模型。
将建立的所有FEA模型表面应变数据全部输出, 计算相同应变监控点位置在不同FEA模型中应变值的方差。当方差较大时, 可认为该位置对裂纹敏感度高, 则应变数据隐含的裂纹信息(如裂纹长度、裂纹方向等)较多, 应变监控点优先设置在敏感度较高的位置。根据结构自身状况以及应变采集方式, 确定应变采集位置及个数; 应变采集位置应避免相互干扰, 采集方式与位置应避免干扰裂纹扩展过程。
为了增强模型预测能力, 提高模型的鲁棒性, 从FEA结果提取应变数据时, 应主动引入应变采集位置偏差和角度偏差, 分别对应了在实际粘贴应变片时可能存在的位置偏差与角度偏差。假设应变片粘贴位置 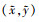 符合正态分布, 其均值为预定位置(x, y), 方差分别为σx, σy, 即
符合正态分布, 其均值为预定位置(x, y), 方差分别为σx, σy, 即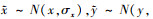 σy); 类似地, 粘贴角度
σy); 类似地, 粘贴角度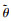 也符合正态分布, 均值为预定角度θ, 方差为σθ, 即
也符合正态分布, 均值为预定角度θ, 方差为σθ, 即 。根据具体结构应变片粘贴情况设置σx, σy与σθ。按照概率分布随机选取l组应变监控点位置和角度的组合, 即
。根据具体结构应变片粘贴情况设置σx, σy与σθ。按照概率分布随机选取l组应变监控点位置和角度的组合, 即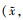
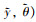 , 采集每组对应的应变值, 最终输出l×nm组FSD。
, 采集每组对应的应变值, 最终输出l×nm组FSD。
由于应变片实测采集时存在零漂现象, 应变片采集的应变值与实际应变值可能存在偏差, 若直接采用应变片采集的应变值作为输入时, 模型的鲁棒性较差。此外, 应变值与外载荷大小有关, 应变值不同的2组数据可能对应相同的裂纹长度, 这导致模型所需训练数据增多、预测精度降低等问题。为解决上述问题, 本文提出一种基于测点应变之间关系的等效应变法。
采用裂纹尖端小范围屈服假设, 应变监控点的应变值与外载荷呈线性关系。对于给定的监控点k(如图 2所示), 定义其等效应变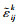 为
为
式中: ΔFa表示载荷Fa的变化值(a=1, 2);Δεijk表示ΔFa引起监控点k的应变变化(i, j∈(1, 2)), p是应变监控点的总个数。
由(1)式可知, 对于任意给定的含裂纹结构, 当裂纹没有发生扩展, 外载变化ΔFa时, 若Δεijk/ΔFa不变, 则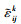 不变, 消元后结果显示
不变, 消元后结果显示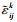 仅与应变监控点Δεijk有关, 而与ΔFa无关。
仅与应变监控点Δεijk有关, 而与ΔFa无关。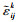 消除了载荷绝对量的影响, 仅体现了由于裂纹长度变化引起不同监控点之间应变数据变化的关系。
消除了载荷绝对量的影响, 仅体现了由于裂纹长度变化引起不同监控点之间应变数据变化的关系。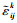 是用于训练机器学习模型的输入数据。
是用于训练机器学习模型的输入数据。
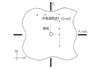 |
图2 含裂纹结构的应变监控示意图 |
1.3 基于循环对抗网络方法的裂纹量化模型修正方法
为了解决实际结构试验结果与FEA数值计算结果之间存在偏差, 采用CycleGAN模型实现试验结果与模拟计算结果之间的映射[24]。CycleGAN常用于实现图像风格转换功能的生成对抗网络(generative adversarial networks, GAN), 本文借鉴CycleGAN网络架构处理有限元数值计算应变数据与试验数据, 建立两者映射关系。在实时预测的过程中, 通过CycleGAN修正模型将试验数值映射为有限元数值计算结果, 将此结果输入到CM、QM, 从而提高模型的预测精度。
CycleGAN用于训练2个生成器G, 以及2个判别器D, 并实现2种数据相互的转换, CycleGAN结构如图 3所示。
从图中可以看出CycleGAN含有2个生成器(generator, G), 其中生成器X2Y(GX2Y)将X生成为Y, 生成器Y2X(GY2X)将Y生成为X; 2个判别器(discriminator, D), 其中判别器X(DX)判别X, 判别器Y(DY)判别Y。XI是X的数据集, 通过GX2Y生成假的Y数据集(YF), YF通过GY2X生成新的X数据集并定义为XCycle。将XI和YF分别代入DX以及DY, 训练判断结果分别为真实(1)和假(0)。同理, YI是Y的数据集, 通过GY2X生成假的X数据集(XF), XF通过GX2Y生成新的Y数据集并定义为YCycle。将YI和XF分别代入DY以及DX中判断, 训练判断结果分别为真实(1)和假(0)。
本文CycleGAN采用的损失函数L如(2)式所示, 共包括LGAN, LCycle, Lsimilarity三部分, 其中α和β为超参数, 是调整LCycle和Lsimilarity占总损失函数值的权重系数, 一般在模型训练时进行试凑, 以最终输出的XF与XI、YF与YI相似原则为标准确定出最佳值, 通常α, β均采用大于10的值。
从图 3可知, 判别器D可以分辨真假数据, 尽可能将真实输出判别成1, 假数据判别成0;生成器G目的是生成尽可能与另一种数据相似的假数据, 并且可以骗过判别器的判断。XCycle和YCycle要尽可能与输入的XI和YI相似。通过上述过程可实现XI和YI数据之间的转化。进而得出损失函数各部分的目的如下:
1) LGAN包括LGAN-X和LGAN-Y, 其目的是保证生成器和判别器相互进化, 进而保证生成器可以产生更真实的另一种数据集以及判别器可以准确判断是否为真实数据, 如(3)~(5)式所示
式中:LGAN-X(GX2Y, DY, X, Y)表示XI转化为YI的损失值;pdata(y)表示数据YI的数据样本分布;Ey~pdata(y)[logDY(y)]表示满足YI数据样本分布的logDY(y)分布函数期望值, 其余函数含义同理。
2) LCycle目的是满足生成的XCycle和YCycle尽可能与XI和YI相似, 即GY2X(GX2Y(XI))≈XI, GX2Y(GY2X(YI))≈YI, 如(6)式所示
3) 为增强生成器生成的假数据与真数据的相似性, 本文提出增加一个损失函数为相似损失函数Lsimilarity。由于拥有与试验数据相同裂纹长度的FEA模型, 可从FSD随机选取与试验裂纹长度相同的数据进行匹配, 计算相似损失函数, 如(7)~(8)式(M表示为均方误差损失函数, 如(7)式所示, 可求得共有N组数据的yi, 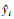 的M)
的M)
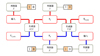 |
图3 CycleGAN结构图 |
1.4 基于神经网络的裂纹尺寸分类方法与裂纹长度量化方法
由于当裂纹较短时, 应变数据对裂纹长度的变化不敏感, 应减小裂纹较长时的应变训练数据的干扰, 通过采用不同裂纹长度范围的应变值训练多个模型, 可以提高整体裂纹长度的预测能力。为此, 有必要将结构裂纹尺寸划分范围。本文建立CM用于对裂纹尺寸进行分类,如图 4所示。
首先初步训练一个裂纹长度量化模型, 观测预测结果与实际结果的偏差, 找到预测结果距实测结果偏差较大的实测裂纹长度, 在此处设置裂纹长度阈值a0, 可设置多个阈值以增强裂纹长度的预测。本文只设置一个阈值, 当裂纹长度均小于a0时判断为短裂纹, 反之则为长裂纹, 并定义长裂纹时输出为1, 短裂纹则为0。采用1.2节方法对应变数据进行预处理, 获得的等效应变作为输入, 裂纹长度范围值(0或1)作为输出, 据此建立CM模型, 中间神经元采用ReLu激活函数, 其结果用Sigmoid激活函数激活, 进而得到[0, 1]的数值, 当结果大于0.5被判断为长裂纹, 反之被判断为短裂纹。其损失函数采用交叉熵损失函数(见(9)式)。
裂纹量化模型(QM)含有多个子模型(sub-QM), 子模型个数比CM设置的阈值个数多一个, 最终将多个sub-QM组合形成QM。本文采用了2个子模型, 分别为短裂纹长度量化模型(short cracks sub-QM, s-sub-QM)与长裂纹长度量化模型(long cracks sub-QM, l-sub-QM)。
采用基于神经网络的机器学习方法, 将等效应变中符合短裂纹条件的数据进行训练, 以建立s-sub-QM, 符合长裂纹条件的数据进行训练, 以建立l-sub-QM, 并用ReLu激活函数激活来解决回归问题。当裂纹尺寸范围被CM分类后, 将等效应变代入符合裂纹尺寸范围分类的sub-QM, 进而得到预测裂纹长度。
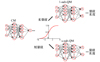 |
图4 CM与QM关系图 |
2 中心带孔板裂纹长度实时预测
目前中心带孔板研究较成熟, 在试验过程中可实现对其他因素的有效控制, 所以中心带孔板常作为材料性能、力学方法探究的对象, 本文采用中心带孔板作为方法验证的对象。
2.1 有限元模型的建立
本文实例采用的带孔板长300 mm, 宽60 mm, 厚2 mm, 其中孔的直径6 mm, 如图 5所示。带孔板材料为LY12-CZ, 弹性模量71 000 MPa, 泊松比0.33。定义中心孔的两侧分别预制长为a1和a2的裂纹。对比了2类裂纹长度组合: ①对称裂纹(symmetric crack, SC): a1=a2=1 mm; ②非对称裂纹(non symmetric crack, NSC)a1=1 mm, a2=3 mm。
设a1∈[1, 20], a2∈[1, 20], d=1, 则裂纹长度共有400种可能的组合, 依次建立这些组合下的FEA模型。为加速模型的计算, 将结构简化为平面应力模型, 典型网格及边界条件如图 6所示, 模型两端均用多点约束(multi-point constraints, MPC)的梁约束在左右2个参考点上, 对左侧端点施加固支约束, 右侧端点施加简支约束并施加结构长度方向上1 kN的载荷。在模型距孔心较远处划分网格尺寸为2 mm的稀疏网格, 在距孔心较近时用网格尺寸为0.5 mm的密集网格, 裂纹尖端网格类型为六节点二次三角形单元(CPS6), 其余网格类型为八节点二次四边形单元(CPS8)。
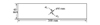 |
图5 中心带孔板试件示意图 |
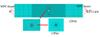 |
图6 有限元模型示意图 |
2.2 有限元模型表面应变对裂纹灵敏度分析
在模型可能产生裂纹的位置, 选取其附近区域作为应变对裂纹长度敏感度的考察区, 用于确定应变监控点位置, 如图 7所示。定义孔心为(0, 0)点, 模型长度方向为x轴, 宽度方向为y轴。当应变监控点距孔心较远时, 应变对裂纹长度变化不敏感, 因此仅需分析距孔较近区域。
输出每个模型的表面应变, 并用相同位置、不同模型的x方向应变分量计算方差, 当方差较大时, 说明该点较敏感。不同位置应变方差的等高图如图 7所示。
由图 7可以看出, 靠近裂纹位置的敏感度较高, 远离裂纹位置的敏感度较低。由此, 可总结得出应变监控点的选取原则: ①应变监控点个数越少越好; ②应变值对裂纹长度的改变较敏感; ③应避免应变监控点相互干扰, 且应避开裂纹扩展路径。
根据应变对裂纹敏感度分析, 可以看出在Y=±9与±20附近出现波峰, 应尽可能选取这些位置。
为增加模型的鲁棒性, 应变监控点的位置 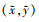 满足统计分布特征, 即
满足统计分布特征, 即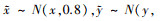 0.8);应变采集角度满足统计分布特征
0.8);应变采集角度满足统计分布特征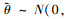 1)。每个FEA模型输出60组数据, 共24 000组数据, 采用基于测点应变之间关系的处理方法(见(1)式)对数据进行处理, 得到等效应变, 选20%作为验证数据, 80%作为训练数据进行模型训练。
1)。每个FEA模型输出60组数据, 共24 000组数据, 采用基于测点应变之间关系的处理方法(见(1)式)对数据进行处理, 得到等效应变, 选20%作为验证数据, 80%作为训练数据进行模型训练。
最终隐藏层设置为[1 240, 640, 320, 160], 采用Adam优化器优化, 并采用MSE损失函数作为模型预测强度的评判标准。通过表 1最终选定(6, -20), (6, -9), (6, 0), (6, 9), (6, 20)应变监控点组合进行训练和试验。
 |
图7 模型应变对裂纹长度方差分析图 |
应变监控点组合与对应损失值
2.3 试验结果处理与分析
采用PLD-100疲劳试验机(±100 kN)开展单孔板试件的疲劳试验, 试件监控点粘贴BX120-3AA应变片, 并用DH-5921动态应力应变测试分析系统记录实时应变数据。试件背面粘贴标尺, 借助数码显微镜直读裂纹长度, 记录裂纹出现时间, 如图 8所示。为了体现复杂载荷下的模型预测能力, 试验采用图 9所示的随机载荷谱。
应变值测量会有零漂现象, 且随着时间的推移, 零漂现象较严重, 如果直接采用应变的绝对量会产生较大误差, 采用应变值变化的相对量会显著减小误差。因此, 本文将应变变化量作为应变输入。典型的监控点应变与时间变化关系如图 10所示(其中每一个时间刻度是1/20 s, 图中A, B, C, D, E均为应变监控点)。
 |
图8 试验试件 |
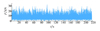 |
图9 中心孔板疲劳裂纹扩展试验载荷谱 |
 |
图10 带孔板疲劳试验应变监控点结果(截取) |
2.4 模型修正分析
基于测点应变之间关系处理有限元模拟数据与试验数据, 建立CycleGAN模型, 其2个生成器分别用于由试验数据生成FSD, 以及由FSD生成试验数据; 2个判别器分别用于判别试验数据和FSD是否真实。
本实例模型所采用的机器学习模型参数如表 2所示, 所有模型均采用Adam优化器加速收敛。CycleGAN模型采用Leaky ReLu激活函数来加快收敛, 在损失函数(2)式中令参数α=10, β=15, 训练CycleGAN模型需要的试验数据来源于中心带孔板试验, 数值计算数据来源于有限元模型计算结果, 为了增加模型鲁棒性, 每次迭代更新时, 均需要重新随机选取裂纹长度相等的数值计算数据与试验数据。
CycleGAN中的判别器与CM最后一层采用Sigmoid激活, 输出[0, 1]的数值, 判别器输出1代表为真。CM输出1代表是长裂纹。学习率为0.000 1训练20次接近收敛, 最终准确度约为93%, 且对较小裂纹尺寸分类准确度较高。QM共有2个子模型, 长裂纹模型(l-sub-QM)与短裂纹模型(s-sub-QM), 学习率均设置为0.000 1, 训练50次接近收敛, 最终l-sub-QM的MSE损失值为0.000 444 5, s-sub-QM的MSE损失值为0.001 245, 长裂纹预测精度略高于短裂纹预测精度。
模型训练完成后, 将SC, NSC各2个试件进行试验并定义试件编号分别为SC_1、SC_2、NSC_1、NSC_2。实时采集监控点的应变值, 做等效应变值处理后输入到模型中, 得到当前裂纹长度预测结果并进行分析。
绘制SC、NSC试件经过CycleGAN模型修正的预测数据(prd.data)、未经过CycleGAN模型修正的预测数据(un-prd.data)以及相应的试验数据(exp.data),如图 11~12所示。图中以孔心为原点, 横轴沿板宽方向, 表示裂尖到孔心的距离; 纵轴为循环谱块数。从两图中可以看出未修正的预测在裂纹较长时较为准确, 但裂纹较短时精度较低。CycleGAN模型修正可有效地提高短裂纹长度范围的预测精度。对称裂纹模式的应变变化简单, 应变含有的裂纹信息较少, 其裂纹预测精度比非对称模式的裂纹预测精度稍差。模型精度误差在1 mm之内, 本文方法在带孔板裂纹长度预测中取得了较高的精度。然而, 值得注意的是, 即使对机器学习模型进行了修正, 短裂纹情况下的预测准确性不足, 其主要原因是当裂纹较短时, 应变监控点采集的应变数据含有的裂纹信息不足, 无法准确地反映短裂纹下的裂纹长度。针对该问题, 可在后续研究中探索采取增加应变片数量、在训练数据中增加裂纹扩展方向信息等措施以解决。
机器学习模型结构参数
 |
图11 预制对称裂纹(SC)试件裂纹长度的实测值、预测值与循环谱块数的关系 |
 |
图12 预制非对称裂纹(NSC)试件裂纹长度的实测值、预测值与循环谱块数的关系 |
3 结论
本文建立了基于深度学习的结构疲劳裂纹量化模型, 在外载未知情况下, 仅通过应变监控数据可以较为准确地实现裂纹长度的实时预测。通过借鉴CycleGAN网络结构建立了修正模型, 实现了试验数据与数值计算数据的映射, 减小了因两类数据之间存在偏差造成的误差; 同时, 建立了裂纹尺寸的分类模型, 对不同分类的裂纹, 分别建立了预测其裂纹长度的量化模型子模型, 并组成最终的量化模型, 进而实现了裂纹尺寸的精确预测。与试验结果对比表明, 裂纹长度预测误差小于1 mm; 裂纹长度预测精度与裂纹长度范围存在关系, 当裂纹较短时精度略差于长裂纹情况, 可通过增加应变监控点数量的方式提高。本文提出的模型和方法可实现裂纹长度的实时在线预测, 为飞机的检修与维护、寿命管理、寿命监控等提供理论依据。
References
- CHEN Zhiming, TANG Ning, FAN Huafei. Flight load modeling method optimized for complex structures[J]. Advances in Aeronautical Science and Engineering, 2022, 13(2): 45–50. [Article] (in Chinese) [Google Scholar]
- YANG Zhichun, YU Zhefeng Progress of damage detection for structural health monitoring Advances in Mechanics 2004 342 215 223 [Article] (in Chinese) [Google Scholar]
- CHANG Qi, YANG Weixi, ZHAO Heng, et al. A multi-sensor based crack propagation monitoring research[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(2): 226–237. [Article] (in Chinese) [Google Scholar]
- PARIS P, ERDOGAN F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4): 528–533. [Article] [CrossRef] [Google Scholar]
- WALKER K. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum[J]. Effects Environ Complex Load History Fatigue Life, 1970, 462: 1–14 [Google Scholar]
- FOREMAN R G, PEARY V E, ENGLE R M. Numerical analysis of crack propagation in cyclic-loaded structures[J]. Journal of Basic Engineering, 1967, 89(3): 459–463. [Article] [CrossRef] [Google Scholar]
- HU Changhua, SHI Quan, SI Xiaosheng, et al. Data-driven life prediction and health management: state of the art[J]. Information and Control, 2017, 46(1): 72–82. [Article] (in Chinese) [Google Scholar]
- ZHANG Weifang, HE Jingjing, YANG Jinsong, et al. Research status on structural health monitoring technology for aircraft structures[J]. Aeronautical Manufacturing Technology, 2017(19): 38–47. [Article] (in Chinese) [Google Scholar]
- RENAUD G, LIAO M, BOMBARDIER Y. Demonstration of an airframe digital twin framework using a CF-188 full-scale component test[C]//Proceedings of the 30th Symposium of the International Committee on Aeronautical Fatigue, Krakow, 2019 [Google Scholar]
- DONG Leiting, ZHOU Xuan, ZHAO Fubin, et al. Key technologies for modeling and simulation of airframe digital twin[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(3): 113–141. [Article] (in Chinese) [Google Scholar]
- CAO Jun. Research on real-time structural health monitoring for crack growth[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006 (in Chinese) [Google Scholar]
- WU Lei, JI Guoyi. Application of convolutional neural network for on-line structural health monitoring[J]. Noise and Vibration Control, 2009, 39(4): 200–204. [Article] (in Chinese) [Google Scholar]
- DEANS W F, RICHARDS C E. A simple and sensitive method of monitoring crack and load in compact fracture mechanics specimens using strain gages[J]. Journal of Testing and Evaluation, 1979, 7(3): 147–154 [CrossRef] [Google Scholar]
- CROCOMBE A D, ONG C Y, CHAN C W M, et al. Investigating fatigue damage evolution in adhesively bonded structures using backface strain measurement[J]. The Journal of Adhesion, 2002, 78(9): 745–776 [CrossRef] [Google Scholar]
- NEWMAN JR J C, DAWICKE D S, SESHADRI B R. Residual strength analyses of stiffened and unstiffened panels——part Ⅰ: laboratory specimens[J]. Engineering Fracture Mechanics, 2003, 70(3/4): 493–507 [CrossRef] [Google Scholar]
- ANGULO N, YANG H, TANG J, et al. Structural health monitoring of crack initiation and growth in mooring chains using FEA methods for acoustic emission characterisation[J]. Journal of Acoustic Emission, 2019, 36: S107–S111 [Google Scholar]
- WANG M, FENG S, INCECIK A, et al. Structural fatigue life prediction considering model uncertainties through a novel digital twin-driven approach[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 391: 114512 [CrossRef] [Google Scholar]
- LI C, MAHADEVAN S, LING Y, et al. Dynamic Bayesian network for aircraft wing health monitoring digital twin[J]. AIAA Journal, 2017, 55(3): 930–941 [CrossRef] [Google Scholar]
- PANG Jie. Research on key technologies for image recognition for surface cracks of concrete dams[D]. Mianyang: Southwest University of Science and Technology, 2021 (in Chinese) [Google Scholar]
- WANG Hunwei. Research on load identification algorithm of aircraft based on neural network[D]. Hangzhou: Zhejiang University, 2018 (in Chinese) [Google Scholar]
- TRIVAILO P M, CARN C L. The inverse determination of aerodynamic loading from structural response data using neural networks[J]. Inverse Problems in Science & Engineering, 2006, 14(4): 379–395 [CrossRef] [Google Scholar]
- ZHENG Xing, WANG Zhiguo. Fatigue crack detection method of aircraft structure based on measured strain[J]. Machine Building and Automation, 2021, 50(2): 236–240. [Article] (in Chinese) [Google Scholar]
- ZHU J Y, PARK T, ISOLA P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]//2017 IEEE International Conference on Computer Vision, 2017: 2242–2251 [Google Scholar]
- QIN Y, WU X, LUO J. Data-model combined driven digital twin of life-cycle rolling bearing[J]. IEEE Trans on Industrial Informatics, 2022, 18: 1530–1540 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 基于应变监控数据的结构疲劳裂纹量化模型方法流程图 |
| In the text | |
 |
图2 含裂纹结构的应变监控示意图 |
| In the text | |
 |
图3 CycleGAN结构图 |
| In the text | |
 |
图4 CM与QM关系图 |
| In the text | |
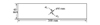 |
图5 中心带孔板试件示意图 |
| In the text | |
 |
图6 有限元模型示意图 |
| In the text | |
 |
图7 模型应变对裂纹长度方差分析图 |
| In the text | |
 |
图8 试验试件 |
| In the text | |
 |
图9 中心孔板疲劳裂纹扩展试验载荷谱 |
| In the text | |
 |
图10 带孔板疲劳试验应变监控点结果(截取) |
| In the text | |
 |
图11 预制对称裂纹(SC)试件裂纹长度的实测值、预测值与循环谱块数的关系 |
| In the text | |
 |
图12 预制非对称裂纹(NSC)试件裂纹长度的实测值、预测值与循环谱块数的关系 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


