| Issue |
JNWPU
Volume 38, Number 6, December 2020
|
|
|---|---|---|
| Page(s) | 1291 - 1298 | |
| DOI | https://doi.org/10.1051/jnwpu/20203861291 | |
| Published online | 02 February 2021 | |
Initiation and Propagation Characteristics of Multi-Source Fatigue Crack in Superalloy Disk
高温合金盘多源疲劳裂纹萌生及扩展特征
1
College of Energy Engineering, Zhejiang University, Hangzhou 310027, China
2
College of Mechanical and Electrical Engineering, Wenzhou University, Wenzhou 325035, China
Received:
12
February
2020
The multi-source fatigue crack growth characteristics of a turbine disk were studied via high-speed rotating low cycle fatigue test, fracture analysis and crack growth simulation analysis. The results show that the fatigue initiation life N0 of Superalloy disk and its simulation parts is less dispersive and similar, and the S-N0 curve of the material is not conservative to predict the N0 of the disk. The fracture of eccentric hole of disk is multi-source fatigue fracture, and the surface characteristic of the crack L/D decreases rapidly from 7.5 to 2, which is obviously different from the single source fatigue crack growth. Because of the long and thin stress distribution at the eccentric hole and the small dispersivity of GH698 crack initiation life, it's relatively easy to crack on the plane A of the eccentric hole, which is prone to multi-source fatigue. At the stage of a ≥ 1.23 mm, the reverse life of crack propagation fracture of 2# and 5# eccentric holes is consistent, and the error between the simulation value of single source fatigue crack propagation life and the reverse life is below 5%. In the stage of 0.61 mm ≤ a < 1.23 mm, the simulation crack growth rate of 5# eccentric hole of multi-source is close to that of fracture inversion. Accurate simulation analysis of multi-source crack growth needs to define the initial crack accurately, at the same time, consider the influence of existing fatigue damage on crack growth.
摘要
通过高速旋转低周疲劳实验及断口分析、裂纹扩展仿真分析,研究了某涡轮盘多源疲劳裂纹扩展特征。结果显示高温合金盘及其模拟件的疲劳萌生寿命N0分散性较小且相近;直接采用材料的S-N0曲线预测轮盘N0时偏不保守。轮盘偏心孔断口均为多源疲劳断口;裂纹表面特征L/d从7.5快速减小至2,明显不同于单源疲劳裂纹扩展。由于偏心孔处应力分布细长、GH698裂纹萌生寿命分散性小,偏心孔A面各处各自萌生裂纹相对容易,易出现多源疲劳。a≥1.23 mm阶段,2#、5#偏心孔裂纹扩展断口反推寿命变化较一致,单源疲劳裂纹扩展寿命仿真值与之误差在5%以内。0.61 mm≤a < 1.23 mm阶段,5#偏心孔多源裂纹扩展速率仿真值与断口反推值接近。准确的多源裂纹扩展仿真分析不仅需要准确定义初始裂纹,同时还需考虑各处已有的疲劳损伤对裂纹扩展的影响。
Key words: superalloy / turbine disk / LCF / damage tolerance / multi-source initiation
关键字 : 高温合金 / 涡轮盘 / 低周疲劳 / 损伤容限 / 多源起裂
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
伴随着航空事业的发展, 推重比、涡轮前燃气温度及压气机增压比不断提高, 对应用在航空发动机涡轮盘等高温部件的材料力学性能提出了更加严格的要求。涡轮盘在高温、高压和高转速下工作, 承受着交变、复合的工作载荷, 易产生低周疲劳损伤, 疲劳损伤进一步发展会导致涡轮盘疲劳断裂, 从而带来不可挽回的经济损失和人身伤害[1]。2016年10月28日, 美国航空公司的一架波音767客机在起飞时其装有的CF6-80C2B6发动机高压涡轮二级盘发生非包容破裂, 碎块打穿燃油箱, 引发大火, 将2亿美元的客机烧毁, 并导致1名乘客重伤、21人轻伤。通过观察轮盘残骸断面, 发现轮盘盘心处有微米级氧化物造成的条纹和微裂纹, 在长期处于低周疲劳条件下裂纹逐渐增长并导致轮盘爆裂[2]。高温合金有较高的高温强度、出色的抗氧化能力、良好的蠕变性能、卓越的疲劳性能和断裂韧性等, 被广泛用于涡轮盘等航空发动机热端部件。因此, 开展高温合金低周疲劳损伤与断裂研究具有非常重要的意义。目前, 国内外基于材料试样级、特征模拟件级疲劳实验, 开展了众多高温合金理论分析、断口分析及裂纹扩展仿真分析等[3-9]。针对主裂纹周围形成的微裂纹群问题, 侯俊玲等[10]利用M积分研究了镍基合金材料中的微裂纹增韧问题。数值模拟了不同长度微裂纹对于主裂纹的影响, 结果表明, 微裂纹越长对于材料的增韧效果越明显。朱强[11]观察并分析了GH698合金低周疲劳后的滑移带、位错组态和断口形貌,研究了其低周疲劳断裂机理。通过使用新的平均应力公式, 同时考虑应力梯度和尺寸效应的影响。刘红彬等[12]获得了改进后的疲劳构件寿命预测方法。通过材料级间盘模拟实验件疲劳实验,其对寿命预测模型所需的寿命预测方程中的参数进行拟合, 进一步通过与涡轮盘螺栓孔模拟件疲劳实验结果的比较,评价了新方法的精度。基于断口反推理论分析理论, 赵荣国[13]指出不同应力条件下GH4133B合金的反推理论载荷与实验载荷的相对误差均在15%以内。根据稳定扩展区疲劳条带反推得到的裂纹扩展方程, 仍可较为精确地描述GH4133B合金全阶段的疲劳裂纹扩展规律。CLÁUDIO等[14]提出一套复杂结构的三维裂纹断裂力学参数计算方法, 估算燃气涡轮盘寿命, 与CT试样结果具有较高一致性。基于这些研究成果, 对高温合金涡轮盘结构开展了参数寿命法分析、损伤容限寿命、可靠性分析[15-17]。以粉末冶金夹杂裂纹扩展寿命预测理论为基础, 建立了裂纹扩展可靠性分析的剩余强度干涉模型与寿命干涉模型。采用改进一次二阶矩法分析单个夹杂裂纹扩展的可靠性。刘成立等[18]提出了随机裂纹位置的均值等可能分布的多裂纹分布模型, 用于分析多个夹杂裂纹扩展的可靠性。所提方法被应用于计算某粉末冶金涡轮盘裂纹扩展的失效概率, 分析结果表明夹杂位置距离表面较近的裂纹引起失效的概率大。
以上多裂纹扩展分析研究的条件往往较为理想, 与高温合金多源起裂有较大差别, 涡轮盘寿命预测往往误差较大。因此, 本文基于某型发动机高压涡轮盘低周疲劳裂纹扩展实验, 通过对其进行断口分析及裂纹扩展仿真分析等, 研究了真实条件下其多源疲劳裂纹扩展特征。
1 实验概况
本文研究对象为某高压涡轮盘, 如图 1所示。该涡轮盘上有6个偏心孔:0#-5#, 每个偏心孔有6个表面:A-F。其材料为GH698。根据中国航空动力机械研究所提供的资料及文献[9], 经插值得345℃时该材料力学性能如表 1所示, 其裂纹扩展速率满足Paris模型:da/dN1=1.48×10-13(ΔK)3。其中, N1为疲劳裂纹扩展寿命, a为疲劳源至观察点的距离; da/dN1和应力强度因子ΔK的单位分别为mm/次、MPa·mm0.5。
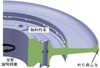 |
图1 涡轮盘简化模型 |
GH698材料数据(345℃)
根据空军装备研究院第一所及文献[10]GH698材料试样及特征模拟件高温低周疲劳实验可知, 材料疲劳裂纹萌生寿命N0与应力水平S近似呈双对数线性关系, 如图 2曲线所示。其中, 曲线Ⅰ为S-N0中值曲线; 曲线Ⅱ为置信度γ=95%、可靠度p=99.9%的S-N0单侧置信下限曲线。特征模拟件的N0则基本在曲线Ⅰ、Ⅱ间小幅波动。
 |
图2 S-N0曲线 |
涡轮盘在ZUSTD高速旋转实验台上开展高温交变转速低周疲劳实验。实验温度为345℃均温。上限转速为21 300 r/min, 下限转速为1 000 r/min。进行弹塑性有限元计算, 其载荷、约束如图 1所示, 材料模型使用双线性模型(由表 1计算真实应力、应变, 并近似计算得切线模量为4.57 GPa)。经弹塑性有限元计算, 轮盘偏心孔A面的最大综合应力σVon, max为748 MPa, 最大周向应力σθ, max为892 MPa; 偏心孔B面σVon, max为765 MPa, σθ, max为865 MPa; 均位于其中部位置。最大应力均超过了材料的屈服强度; 周向为最大主应力方向, 其他方向应力较小, 可近似为单轴应力状态, S≈σθ, max。应力云图见图 3。
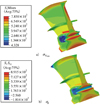 |
图3 应力云图(单位:MPa) |
经50 299次循环,涡轮盘沿2#、5#偏心孔所在子午截面破裂成两大块。实验过程中, 涡轮盘进行了5阶段拆解、着色检测。图 4为50 280次循环后2#偏心孔检测照片, ABCD面均已出现明显裂纹; 图 5为偏心孔ABC面裂纹表面长度(LA, LB, LC)变化曲线。由图 5可知, A面最先萌生裂纹, B面次之, C面最后萌生; 对于2#偏心孔, A面N0在35 000~40 000次间(N1在10 299~15 299间), B面N0在40 000~42 500次间, C面N0大于42 500次; 在40 000~42 500次循环间, 1#、2#的LA出现了平缓增长的特征; 各裂纹扩展前期LA, LB的变化普遍具有比后期大的异常特征。裂纹扩展路径基本上与周向垂直, 细观上表现为曲折扩展。
 |
图4 2#孔C、D面裂纹(50 280次循环) |
 |
图5 裂纹表面长度变化曲线 |
根据检测结果, 将轮盘各偏心孔A、B面的(σθ, max, N0)绘入图 2。由图 2可知, 轮盘偏心孔A、B面的(σθ, max, N0)与模拟件实验结果较一致, 验证了模拟件设计方法的准确性。同时, 其基本位于曲线Ⅰ下、曲线Ⅱ上, 说明工程构件与材料标准试样在疲劳寿命分布规律上存在较大差异。该差异主要受到以下因素影响:
1) 尺寸大小
构件偏心孔处的截面尺寸明显比材料标准试样大。而随构件尺寸的增大, 疲劳强度降低。
2) 表面状态
涡轮盘和模拟件的A、B面未经表面磨光加工处理, 而材料标准试样以磨光方法制备。表面加工方法不同导致表面光洁度不同, 这直接影响到构件的疲劳强度。
3) 载荷因素影响
受结构影响及温度加载条件限制, 涡轮盘实际并非处于均匀温度场。
4) 材料及工艺
标准试样取自该轮盘半成品不同的部位和方向, 具有不同于构件特征部位的疲劳强度。
2 断口分析
疲劳断口的形貌特征与材料的组织特点、外加载荷的大小和状态以及环境因素等有关。因此, 观察和分析疲劳断口形貌对于研究裂纹的萌生、扩展及疲劳断裂机制有着重要的意义。除2#、5#偏心孔断口, 其余偏心孔断口由人工打开。
2.1 断口宏观形貌分析
各偏心孔断口宏观形貌照片如图 6所示。各疲劳断口宏观形貌特征相似, 无明显塑性变形, 为韧性疲劳断裂, 存在多个疲劳源区域, 高温氧化作用导致断口出现了黑色或褐色。多个疲劳源区域共存是镍基高温合金低周疲劳的一个典型特征。疲劳裂纹从偏心孔A面及B面多源起裂, 2#偏心孔受螺栓挤压作用同时从C面起裂。疲劳源区域表面较粗糙, 平整的小平面较少, 各小平面间有明显的台阶。相较于疲劳源区域, 疲劳扩展区域表面更粗糙, 不同部位高度差异比较大, 局部有高差达0.5 mm、长3 mm的疲劳棱线。受C面疲劳源影响, 2#偏心孔疲劳区明显较大; 0#偏心孔疲劳区明显小; 其余4个偏心孔的疲劳区形状相似, 显示该涡轮盘偏心孔处的疲劳寿命N波动较小。
 |
图6 断口宏观照片 |
根据断面疲劳区宏观形貌特征及裂纹表面长度检测结果, 可得各断口A、B面裂纹扩展形状参数L/d随裂纹深度d的变化曲线, 如图 7实点所示。由图可知, 裂纹萌生初期, 各断口的裂纹深度d较小, 但L/d较大, 疲劳区呈细长状; 随着裂纹扩展, L/d快速减小。
 |
图7 d-L/d曲线 |
2.2 断口微观形貌分析
使用扫描电子显微镜(SEM)对2#、5#偏心孔疲劳断口指定路径(见图 6c)、6f))进行观察。指定路径从一处疲劳源开始。图 8为2#偏心孔断口A面指定路径典型位置的SEM照片。由分析可知:
 |
图8 疲劳断口微观形貌 |
疲劳源区未见冶金或加工缺陷; 疲劳微裂纹在合金疲劳试样表面不同位置的晶界、孪晶界或者脆性碳化物处开始萌生, 沿着径向方向扩展, 主要表现为沿晶开裂形式, 类解理河流花样。
疲劳扩展区断口形貌上有光滑的沿晶断裂表面, 局部区域存在类解理台阶特征、河流花样特征和二次裂纹特征。令1.23 mm≤a≤9.10 mm为区间1, 0.61 mm≤a≤1.23 mm为区间2, 1.23 mm≤a≤6.46 mm为区间3。2#偏心孔A面在区间1、5#偏心孔A面在区间2和区间3, 可见细密清晰的疲劳条带特征。疲劳瞬断区断口形貌上存在大量韧窝。
2.3 断口定量反推
在裂纹稳定扩展阶段, 疲劳裂纹扩展受应力状态控制, 应力强度因子的幅值(ΔK)为裂纹扩展的控制变量, 断口上会形成疲劳条带。通常认为, 每一条疲劳条带对应一次载荷循环。因此, 可根据断口疲劳条带宽度计算裂纹扩展速率(da/dN1)[19]。令2#、5#偏心孔A面深度方向裂纹扩展速率断口分析值分别为(da/dN1)2t,(da/dN1)5t, 如图 9a)所示。由该图可知, a-(da/dN1)2t曲线近似呈双对数线性关系; a-(da/dN1)5t曲线明显分成两段, 开始时(da/dN1)5t线性增大, 但a=1.5 mm后其开始不断降低, a=3 mm后其又开始线性增大。
 |
图9 裂纹扩展特性曲线 |
定量反推疲劳循环次数主要采用列表梯形法, 见公式(1)。自a=1.23 mm起,由断口反推获得的2号和5号偏心孔裂纹扩展累积寿命曲线,如图 9b)中的正方形和圆形曲线所示, 2号偏心孔在区间1、5号偏心孔在区间3的裂纹扩展寿命断口反推值分别为(N1)2t=8 462次,(N1)5t=6 926次。(N1)2t,(N1)5t变化曲线如图 9b)所示, 初始阶段(N1)2t比(N1)5t略大, a≥5 mm后两者几乎一致, 因此, a≥1.23 mm阶段裂纹扩展特征差异对N1影响小。5号偏心孔的裂纹扩展寿命断口反推值(N1)5t=8 223次。
3 裂纹扩展对比分析
由文献[14]及多个轮盘分析验证可知, 裂纹稳定扩展阶段裂纹扩展仿真分析具有较高的精度; 裂纹非稳定扩展阶段, 由于屈服大、变形大、动态效应明显, 基于弹性、静态的裂纹扩展仿真分析误差较大, 但是, 由于该阶段裂纹扩展速率大, 裂纹扩展寿命占总裂纹扩展寿命的比例很小, 可忽略该阶段。因此, 本节利用三维裂纹扩展分析软件Franc3D, 结合有限元软件Abaqus, 开展基于线弹性断裂力学理论的单源、多源疲劳裂纹扩展仿真分析。其载荷、约束及裂纹扩展模型等见第一节, 初始裂纹尺寸如下文所述。Franc3D在网格模型中插入初始裂纹, 并对网格进行重新划分; 网格划分完毕后, 调用Abaqus求解器, 计算得到应力、位移等结果; 凭此结果, 计算断裂力学参数, 跟据选取的裂纹扩展模型预测裂纹扩展历程。通过仿真和实验的对比, 研究多源疲劳对裂纹扩展特征的影响, 同时对仿真分析方法的准确性做出评价。
损伤容限设计是假定构件中存在着裂纹, 用断裂力学分析、疲劳裂纹扩展分析和实验验证, 确定这些裂纹扩展速度以及结构剩余强度, 保证在定期检查肯定能发现裂纹之前, 裂纹不会扩展到足以引起破坏。初始裂纹长度的规定主要受现有裂纹无损检测水平限制。在英军标Defence Standard 00971中给出的尺寸是一条长为0.76 mm的表面线裂纹; 在FAA的咨询通告AC33.70-2中指出, 萌生一条可检测的裂纹定义为0.76 mm(长)×0.38 mm(深)的裂纹。因此, 为便于开展单源疲劳裂纹扩展仿真分析, 本文假定其初始裂纹为一半径为0.38 mm的半圆形初始裂纹。同时, 为研究多疲劳源对涡轮盘裂纹扩展的影响, 开展了多源疲劳裂纹扩展仿真分析:依据图 7中L/d的特点并线性外推, 假定偏心孔中部存在L=6.5 mm,d=0.38 mm的细长初始裂纹。
3.1 多源特征成因分析
偏心孔A面σθ随L的变化曲线如图 10所示。由该曲线及图 2中S-N0中值曲线可得到的偏心孔A面不同位置处的萌生裂纹寿命N0L。令ΔN0L为各处N0L相较于σθ, max=892 MPa处N0L的增量。假设在σθ=892 MPa处存在一半径为0.38 mm的初始裂纹, 并令ΔN1p为假设初始裂纹下裂纹扩展至长度L时的循环数。ΔN0L和ΔN1p随L的变化如图 10所示。由该图可知:
 |
图10 裂纹扩展特性曲线 |
L≤18.5 mm时, ΔN0L比ΔN1p小, 因此, 相对于σθ, max=892 MPa处裂纹扩展至偏心孔A面各处, 各处各自萌生裂纹相对容易。因而, 初始时偏心孔表面易出现多源疲劳, 从而具有较高的L/d。之后, 各个疲劳源萌生的裂纹相互融合, 形成一个大裂纹并继续扩展, 此时, L/d下降。
偏心孔B面的σθ比A面的略小, 但具有相似的应力分布, 因而也易见多源起裂。
偏心孔处应力分布特点、高温合金材料裂纹萌生寿命及扩展寿命分布特征导致涡轮盘偏心孔在最大周向应力处出现主裂纹, 同时, 在最大周向应力附近大应力区易出现微裂纹/小裂纹等疲劳损伤。
3.2 多源疲劳裂纹扩展影响分析
令偏心孔A面在单源、多源假设下深度方向的裂纹扩展速率仿真值分别为(da/dN1)s,(da/dN1)m; 区间裂纹扩展寿命为(N1)s,(N1)m。由裂纹扩展仿真分析可得相应的裂纹扩展速率曲线、等寿命曲线, 如图 9所示。表 2为裂纹扩展寿命的比较。由单源和多源仿真分析获得的A面d-L/d曲线如图 7所示。由分析可知:
区间裂纹扩展寿命误差
1) 0.61 mm≤a < 1.23 mm阶段, 对于2#偏心孔, 该阶段未见疲劳条带; 对于5#偏心孔, (da/dN1)s明显比(da/dN1)5t小, (da/dN1)m与(da/dN1)5t接近, 因此, 该区间多源疲劳裂纹扩展仿真具有较高的准确性。a≥1.23 mm阶段, (da/dN1)s与(da/dN1)2t, (da/dN1)5t接近, 而(da/dN1)m比(da/dN1)2t, (da/dN1)5t大。因此, 该区间单源疲劳裂纹扩展寿命仿真值(N1)s与(N1)2t, (N1)5t相差较小, 多源疲劳裂纹扩展寿命仿真值(N1)m则与之相差较大但偏保守。裂纹扩展中期, 多源对裂纹扩展的影响则可以忽略。d-L/d曲线仿真值与断口分析值的变化也反映了这些特点。当d较小时,d-L/d曲线单源仿真值与断口分析值差异巨大,而多源仿真值与断口分析值接近:d增大时,d-L/d曲线单源仿真值与多源仿真值、断口分析随不断接近。
2) 2#偏心孔裂纹扩展中后期, da/dN1整体较高; C面裂纹与A面裂纹融合后, 表面半圆裂纹转变为角裂纹, 同时, 裂纹长度迅速增大, da/dN1急剧增大。因此, C面裂纹与A面裂纹融合后扩展寿命对总N1的影响很小, 可以以A面的裂纹扩展寿命作为2#偏心孔的总N1。
3) 裂纹扩展初始时的多源起裂是影响裂纹扩展仿真分析精度的主要方面, 但多源疲劳裂纹扩展仿真分析未能准确地反应5#偏心孔的(da/dN1)5t在a=1.5 mm≤a≤3 mm 间的明显变化。多源疲劳仿真的初始裂纹形状与高应力区形状相似, 一定程度上考虑了多源起裂这一现象, 但是, 其对初始裂纹的定义过于简单, 同时, 没有考虑各处已有的疲劳损伤对裂纹扩展的影响。Hutchinson[20]指出微裂纹的出现引起局部材料刚度的下降和残余应力的释放,进而导致宏观裂纹尖端应力场的再分布。
工程中, 通过掌握d-L/d曲线的规律, 选择一个细长的初始裂纹开展多源疲劳裂纹扩展计算, 虽误差较大, 但能避开复杂的多源起裂问题, 获得保守的裂纹扩展仿真值, 为确定表面裂纹检测周期等提供一定依据。
4 结论
通过某高温合金盘高速旋转低周疲劳实验及断口分析、裂纹扩展仿真分析, 研究了高温合金多源疲劳裂纹扩展特性, 结果表明:
1) 轮盘偏心孔A、B面及模拟件的疲劳萌生寿命N0分散性较小且相近, 分布于材料S-N0中值曲线、S-N0下限曲线(γ=95%、p=99.9%)间; 直接用材料S-N0曲线预测轮盘N0时偏不保守。
2) 裂纹扩展初期, 各断口裂纹深度d较小, 但L/d较大、疲劳区呈细长状; 之后L/d随着裂纹扩展快速减小, 具有明显不同于单源疲劳裂纹扩展特点。偏心孔断口均为多源疲劳断口; 2#偏心孔1.23 mm≤a≤9.10 mm、5#偏心孔1.23 mm≤a≤6.46 mm可见细密清晰的疲劳条带特征。
3) 由弹塑性有限元分析及单源裂纹扩展仿真分析可知, 相对于σθ, max=892 MPa处裂纹扩展至偏心孔A面各处, 各处各自萌生裂纹相对容易。因而, 初始时偏心孔A面易出现多源疲劳。
4) a≥1.23 mm阶段, 2#、5#偏心孔裂纹扩展寿命断口反推值(N1)2t, (N1)5t变化较一致; 单源疲劳裂纹扩展寿命仿真值(N1)s与(N1)2t, (N1)5t误差在5%以内, 而多源疲劳裂纹扩展寿命仿真值(N1)m的误差达17%。
5) 0.61mm≤a < 1.23mm阶段, 5#偏心孔, (da/dN1)s明显比(da/dN1)5t小, (da/dN1)m与(da/dN1)5t接近, 因此, 该区间多源疲劳裂纹扩展仿真具有较高的准确性。
准确的多源裂纹扩展仿真分析还需要准确定义初始裂纹, 同时, 考虑各处已有的疲劳损伤对裂纹扩展的影响。
References
- Tao Chunhu, Zhong Peidao, Wang Renzhi, et al. Failure and Prevention of Aero-Engine Rotating Component[M]. Beijing: National Defense Industry Press, 2000 (in Chinese) [Google Scholar]
- Chen Guang. A Hidden Defect in the Turbine Disk Result in a Boeing 767 Burned[J]. Aerospace Power, 2019 (6): 56– 58 (in Chinese) [Google Scholar]
- Phillips P J, Unocic R R, Mills M J. Low Cycle Fatigue of a Polycrystalline Ni-Based Superalloy:Deformation Substructure Analysis[J]. International Journal of Fatigue, 2013, 57: 50– 57 [CrossRef] [Google Scholar]
- Abikchi M, Billot T, CRÉPIN J, et al. Fatigue Life and Initiation Mechanisms in Wrought Inconel 718 DA for Different Microstructures[C]//13th International Conference on Fracture, Beijing, China, 2013 [Google Scholar]
- Sweeney C A, Vorster W, Leen S B, et al. The Role of Elastic Anisotropy, Length Scale and Crystallographic Slip in Fatigue Crack Nucleation[J]. Journal of the Mechanics and Physics of Solids, 2013, 61 (5): 1224– 1240 [CrossRef] [Google Scholar]
- Qin Heyong, Chen Gang, Shen Wentao, et al. Analysis of High Temperature Low Cycle Fatigue Properties for GH4698 Alloy[J]. Metal Forming Equipment and Manufacturing Technology, 2014, 49 (6): 92– 96 (in Chinese) [Google Scholar]
- Sweeney C A, O'brien B, Dunne F P E, et al. Strain-Gradient Modelling of Grain Size Effects on Fatigue of CoCr Alloy[J]. Acta Materialia, 2014, 78: 341– 353 [CrossRef] [Google Scholar]
- Wang Huan, Yuan Chao, Guo Jianting, et al. Fatigue Crack Propagation Behavior of GH4698 Alloy[J]. Chinese Journal of Nonferrous Metals, 2015, 25 (1): 23– 29 (in Chinese) [Google Scholar]
- Zheng Xiaomei, Sun Yantao, Yang Xingyu, et al. Design of Low Cycle Fatigue Simulating Specimen for Bolt Holes of a Turbofan Engine High Pressure Turbine Disc[J]. Journal of Aerospace Power, 2018, 33 (10): 2351– 2358 (in Chinese) [Google Scholar]
- Hou Junling, Li Qun, Zuo Hong. Multiple Crack Growth of Nickel Base Alloy Based on M-Integral[C]//2018 National Conference on Solid Mechanics, Harbin, 2018 (in Chinese) [Google Scholar]
- Zhu Qiang. High Temperature Low Cycle Fatigue Behavior and Fracture Mechanism of GH4698 Nickel-Based Alloy[D]. Harbin: Harbin Institute of Technology, 2016 (in Chinese) [Google Scholar]
- Liu Hongbin, Chen Wei, Liu Lin. Prediction Method and Verification of Fatigue Life for a Turbine Disk with Bolt Hole[J]. Journal of Northwestern Polytechnical University, 2019, 37 (4): 744– 750 (in Chinese) [CrossRef] [Google Scholar]
- Zhao Rongguo. Probabilistic Fatigue Crack Propagation Life Prediction of GH4133B Superalloy Used in Turbine Disk of Aero-Engine[J]. Journal of Mechanical Engineering, 2011, 47 (18): 55– 65 (in Chinese) [CrossRef] [Google Scholar]
- CLÁUDIO R A, Baptista R, Infante V, et al. Life Prediction Using Finite Elements in Complex Geometries[C]//Eighth Portuguese Conference on Fracture, 2002 [Google Scholar]
- Beres W, Dudzinski D, Murzionak A. Fatigue Crack Growth Rate Evaluation in a Turbine Disc after Spin Rig Testing[C]//12th International Conference on Fracture, Ottawa, 2009 [Google Scholar]
- Das P S. Three-Dimensional Structural Evaluation of a Gas Turbine Engine Rotor[C]//ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Germany, 2014: 16–20 [Google Scholar]
- Lu Shan, Huang Qiqing. New Method and Application of Damage Tolerance Analysis of Pin Holes in Turbine Disks[J]. Journal of Aerospace Power, 2002, 17 (1): 87– 92 (in Chinese) [Google Scholar]
- Liu Chengli, Lyu Zhenzou, Xu Youliang. Reliability Analysis for the Crack Growth of Powder Metallurgy Turbine Disk[J]. Rare Metal Materials and Engineering, 2006, 35 (2): 232– 236 (in Chinese) [Google Scholar]
- Tao Chunhu, Xi Niansheng, Zhang Weifang. Resent Development of Fractographic Restrostimationon Determining Fatigue Stress[J]. Journal of Aeronautical Materlals, 2000, 30 (3): 158– 163 (in Chinese) [Google Scholar]
- Hutchinson J W. Crack Tip Shielding by Microcracking in Brittle Solids[J]. Aeta Metall, 1987, 35: 1605– 1619 [Google Scholar]
All Tables
All Figures
 |
图1 涡轮盘简化模型 |
| In the text | |
 |
图2 S-N0曲线 |
| In the text | |
 |
图3 应力云图(单位:MPa) |
| In the text | |
 |
图4 2#孔C、D面裂纹(50 280次循环) |
| In the text | |
 |
图5 裂纹表面长度变化曲线 |
| In the text | |
 |
图6 断口宏观照片 |
| In the text | |
 |
图7 d-L/d曲线 |
| In the text | |
 |
图8 疲劳断口微观形貌 |
| In the text | |
 |
图9 裂纹扩展特性曲线 |
| In the text | |
 |
图10 裂纹扩展特性曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


