| Issue |
JNWPU
Volume 38, Number 6, December 2020
|
|
|---|---|---|
| Page(s) | 1299 - 1307 | |
| DOI | https://doi.org/10.1051/jnwpu/20203861299 | |
| Published online | 02 February 2021 | |
Principle and Method for Machining Face Gear with Developable Ruled Surface
可展直纹面面齿轮的加工原理与方法
College of Mechanical Engineering, Xi'an University of Science and Technology, Xi'an 710054, China
Received:
24
March
2020
The tooth surface of a face gear is recognized as un-developable ruled surface in tradition, which result in the problem that face gear generation using simple cutter with high efficiency and accuracy puzzled people for a long time. Applying the traditional shaping method for face gear generation in derivation of the tooth surface position vector, a space straight line equation was established by using this vector, to illustrate that the tooth surface of the traditional face gear could be considered as developable ruled surface constituted by space lines family, the position vectors of the developable ruled surface were established respectively based on involute, rack and considering the spatial position relationship in meshing. Elaboration and proposition of the principle and method that were used to generate the face gear with the developable ruled surface by straight edged cutter in line contact, and representation of the generated surface model. Furthermore the developable ruled surface was compared to the traditional surface, the normal difference between the two kinds of surfaces is on micro-scale. Numerical examples shows that the normal distance is no more than 1/70 of modulus, the developable ruled surface to which was performed simple longitudinal crowning is able to mesh with the involute surface of the pinion correctly, and demonstrates acceptable geometric meshing performance.
摘要
传统上认为面齿轮的齿面为复杂的非可展直纹面,致使利用简单的刀具高效精准加工面齿轮的问题长期困扰着人们。利用面齿轮传统的插齿方法建立齿面位矢方程,以该位矢为参量建立空间直线方程,说明传统面齿轮齿面可视为空间直线族构成的可展直纹面。考虑空间啮合位置关系,分别基于渐开线和齿条建立了该直纹面的位矢方程。阐述了直刃刀具线接触法加工可展直纹面面齿轮的原理和方法并建立了齿面模型。进一步将该可展齿面与传统齿面进行对比分析,2种齿面的法向差异属于微观量,数值计算结果表明法向距离不到模数的1/70,对可展直纹面进行简单的齿向抛物线修形即可与圆柱齿轮渐开线齿面啮合,并呈现较好的几何啮合性能。
Key words: face gear / developable ruled surface / machining method / meshing / straight edged cutter
关键字 : 面齿轮 / 可展直纹面 / 加工 / 啮合 / 直刃刀具
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
面齿轮传动是一种锥齿轮与直齿圆柱齿轮(小轮)啮合的传动机构[1],由于具备某些特定的传动性能,在直升机主减速器、汽车差速器等传动系统中获得了应用。但由于面齿轮加工过程和刀具复杂,致使加工成本高昂,限制了该传动机构的广泛应用。面齿轮的传统加工方法依赖于定义面齿轮齿形曲面的插齿法,一方面需要以插齿刀的渐开线作为各种刀具切削曲面的产形线[2-4],并且为了将啮合局部化,插齿刀一般比小轮多1~3个齿[1],因此刀具廓形的修正、修整费时费力且通用性差;另一方面由于刀具常常为渐开线螺旋面或旋转曲面,刀具与待加工齿面在任意瞬时均为点接触,从而除连续分度加工效率较高之外,单齿分度的加工效率难以满足面齿轮大批量生产的需求[5]。另外面齿轮传统的加工方法还伴随着复杂机床的使用[6]。
鉴于此寻求利用通用刀具的面齿轮线接触单齿分度、甚至连续分度的加工方法,已成为一项重要课题。Kubo等从齿条、齿轮和面齿轮啮合的角度出发,提出了一种用平面刀具加工新型锥齿轮的方法,加工效率提高了10倍,并认为齿轮的齿廓是加工方法的函数[7],但主要针对的是锥齿轮。唐进元等提出了一种面齿轮的数控插铣方法[8],其课题组还研究了面齿轮的刨削方法[9],这两种方法实现了刀具的通用,但刀具均是沿插齿刀渐开线进行仿形加工,因此属于点接触加工方法。格里森的赫尔曼博士提出了一种基于高阶滚比的平面刀具加工面齿轮的方法,其中高阶滚比用于逼近插齿刀的渐开线[10],并阐述了这种方法连续分度加工面齿轮的原理[11],但是齿面偏差大、呈现两片分离的接触印痕。为实现连续的接触印痕,毛石民等针对这种方法提出按预定轨迹走刀可以控制接触印痕,但不能在全齿宽上降低齿面偏差[12]。本文笔者阐述了平面刀具运动规律的综合方法,并对其几何啮合性能进行了预控[13],依然存在齿面偏差大,接触椭圆较短的问题。实际上从面齿轮的齿面形状上看,其齿廓曲线特别接近于直线,虽然Buckingham认为面齿轮的轮齿为变位变齿厚齿条[14],至目前将此认识用于面齿轮的加工还未得到充分的开发。本文基于面齿轮的插齿法,提出面齿轮的可展直纹面,论述其展开方式和过程、阐述其加工原理与方法,说明其相对面齿轮传统齿面的差异并比较其几何啮合性能。
1 面齿轮齿面上的可展直线族
1.1 面齿轮的齿面方程
图 1所示为面齿轮2与插齿刀s(i=s)或小轮1(i=1)啮合的示意图, 设插齿刀或小轮的齿面位置、法向矢量分别为Ri(θi, ui), ni(θi, ui), θi、ui为齿面的曲面参数。若由插齿刀加工面齿轮, 则面齿轮传统理论齿面Σ2的位置、法向矢量可分别表示为
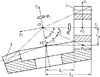 |
图1 面齿轮2与插齿刀s或小轮1的啮合 |
式中:M2ss是插齿刀坐标系Ss到面齿轮坐标系S2的坐标变换矩阵(上标s表示由插齿刀展成, 坐标系均为右手笛卡尔坐标系);γ为轴夹角;L0=(L1+L2)/2, L1、L2分别是由根切和变尖条件确定的面齿轮的内径和外径;rps是插齿刀分度圆半径, 法矢ns第四个元素为0;φs, φ2分别是展成过程中插齿刀与面齿轮的转角, 满足齿数比关系
Ns, N2分别是插齿刀与面齿轮的齿数, 转角φs与曲面参数θs, us满足啮合方程
(1)~(4)式完整地描述了面齿轮的插齿展成过程及其齿面法矢, 其详细信息可见文献[1]。
1.2 齿面上的直线族
为了说明理论齿面Σ2可近似为一系列直线构成的可展直纹面, 可按如下方式在Σ2上建立空间直线方程。
1) 面齿轮节锥面O2*P上齿面Σ2的任一点可用(5)式表示, 式中R2i(i=x, y, z)是矢量R2在其坐标轴i2上的投影, j=1, 2, …, n, n是不小于2的正整数。通过求解(5)式可以得到面齿轮齿面Σ2在其节锥面上离散点的位矢数值, 设为R2j*。
2) 引入与齿面Σ2相同的另一齿面Σ2#, 其位矢和曲面参数由上角标#予以标记, 则可以建立如下直线方程
式中,m为面齿轮副的模数, 式中将直线另外2个点分别限定在齿顶和齿根上, 第五和第六个方程表示直线。上述直线相对坐标轴i2(i=x, y, z)的方向角可以用(7)式表示
1.3 面齿轮齿面上的直线族算例
算例1 面齿轮副的参数为:压力角α=25°; 轴夹角γ=90°; L1=475 mm; L2=565 mm; 模数m=6.35 mm; 插齿刀齿数Ns=30;面齿轮齿数N2=160;小轮齿数N1=30。
利用(5)式、(6)式求解的面齿轮齿面上的直线sj如图 2所示, cj为理论齿面Σ2的齿廓曲线, (6)式的收敛精度为10-9, 由此可知面齿轮齿面的齿廓曲线cj从数值解上看可以认为是直线sj。图 3是该直线相对面齿轮理论齿面Σ2的法向距离, 除内端齿顶处直线sj相对Σ2略有差异之外, 其他部分基本相同, 进一步说明cj可以认为是直线sj。
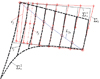 |
图2 面齿轮齿面上的直线族cj |
 |
图3 面齿轮齿面上的齿廓曲线与直线的法向距离 |
图 2中, Σs1, Σs2均属于插齿刀理论渐开线齿面Σs, 前者边界为设计齿面边界, 后者边界为与Σ2完全共轭的边界。L2s是ϕs=ϕ2=0°时两曲面Σ2, Σs的接触线, 为使其经过内端齿顶点和外端齿根点, 图 2和图 3中, L1=477.72 mm、L2=579.32 mm。
直线sj与各坐标轴的方向角如图 4所示, 与x2, z2的夹角之和始终为90°, 即αx+αz=90°, 但两夹角此消彼长, 意味着直线cj的压力角是不断变化的。直线sj与y2不完全垂直, 其最小夹角为88.02°, 最大夹角为90.74°, 这意味着, 即使将直线sj视作为垂直于y2的直线并由该直线族表达面齿轮的齿面, 由此引入的齿面偏差也将是一个微观量。
 |
图4 面齿轮齿面上直线相对坐标轴的方向角 |
2 直线展成面齿轮齿面
2.1 渐开线与变位变压力角直线的共轭
图 2中渐开线tj与齿廓曲线cj完全共轭, cj可以等同于sj, 由该图可以得出以下几点认识:
1) 渐开线tj和0°接触线L2s均位于齿面Σs上, 从端面上看, L2s是渐开线。面齿轮内端(图 2左侧)齿顶齿厚恰好等于插齿刀齿根齿槽宽, 面齿轮外端(图 2右侧)齿根齿厚恰好等于插齿刀齿顶齿槽宽。
2) 渐开线tj自内端至外端与直线cj啮合过程中不断改变始点与终点, 在内端主要是齿根部渐开线(考虑根切), 外端主要是齿顶部渐开线, 这意味着在不同截面(垂直zs)Lj上, 渐开线是变位的。
参考图 1, 插齿刀(小轮)与面齿轮的啮合, 可以视为以O2P作为假想节锥面的两圆锥齿轮啮合, 在O2P上两轮瞬时接触点的线速度相等。因此从截面Lj上看, 插齿刀(小轮)相当于与变位齿条啮合, 又由于面齿轮是一刚性体, 由截面Lj截取的齿条位置并未改变(齿高未变), 则该齿条只能变压力角。
另外点P是插齿刀(小轮)节圆柱面与面齿轮节锥面O2*P的唯一节点, 且在P点有
由于齿面方程、三角函数的非线性, 点P不一定处于齿宽的中间, 但接触轨迹一般位于P点截面处。进一步根据图 1和(8)式还有
3) 假设用直线sj替换cj并使其相切于L2s, 自内端至外端, sj连续改变其压力角就构成了面齿轮的新齿面。显然若将sj绕L2s转至同一角度, 如0°, 再将L2s展成直线, 则该新齿面就被展成了平面, 因此从这个角度说, 该新齿面属于可展直纹面, 并记为Σ2D。
4) 渐开线tj与齿廓曲线cj啮合, tj上各点不在同一截面上, 即有一定的挠曲, 反之若tj上各点在同一截面上, 则cj有一定的挠曲。
该现象通过图 5解释:在面齿轮自cφ2转至aφ2的过程中, 截面Π上的渐开线tj与齿面Σ2的啮合轨迹为q*de*, 并非qde, 因为cj绕z2旋转, 其上的点q、e以半径|pq|=|be|=|gd|=Lj旋转, 因此|q*q|, |e*e|就是端面渐开线tj与cj啮合过程在齿顶和齿根产生的挠曲量。该挠曲量是一微量, 并且随着旋转半径(即传动比N2/N1)的增大而减少, 而面齿轮传动常用于大传动比场合。N1是小轮齿数, 本文中N1=Ns。
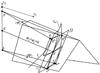 |
图5 渐开线与面齿轮齿面接触的轨迹 |
2.2 由渐开线展成面齿轮齿面
图 6所示为渐开线与变位变压力角直线的关系, 轴线ya始终与渐开线相切于Oa, 切点法矢与ys相交于Ob, Ob到Os的距离rOb与rps之差就是变位量, θs是该直线压力角的变化量。据该图有
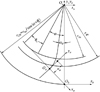 |
图6 渐开线与变位变压力角直线 |
式中, α0=0.5π/Ns-tanα+α, 当Ob始终在节锥面O2P上时, 根据(9)式和图 1可得(12)式。
设ya上动点的矢量为Ra=[0 ua 0 1]T, 将该矢量从坐标系Sa变换到S2中, 即可得到面齿轮齿面Σ2Dinv(上标Dinv表示通过渐开线表达的可展直纹面)的位矢方程
式中, θ=α+θs。实际上由(13)式可知, RsaDinv所表示的是一平面直线族, 由该直线族可以包络出平面渐开线。坐标变换矩阵M2s则使该平面直线族沿齿宽方向重新排列为空间直线族。(13)式通过双参数表达了面齿轮的可展直纹面Σ2D, 其法矢可以表示为
2.3 由齿条展成面齿轮齿面
如上所述, 面齿轮齿面可以视为沿齿宽方向排列的包络平面渐开线的直线族, 因此从齿条与圆柱齿轮的啮合出发, 亦可形成该直线族。
如图 7所示, 当齿条从其初始位置移动rpsφs时, 插齿刀渐开线转过转角φs, 从坐标系Ss中看, 就产生了一条变位变压力角的直线, 并且此时亦有|ObOs|=rOb。需要注意的是:由于是要取包络渐开线的直线族, 而不是取直线族的包络, 因此不能建立表示参数ua、φs函数关系的啮合方程, 本文此处ua是表示直线ya的独立参数, φs是表示从基圆上展开的渐开线的独立参数。此时M2s中的θs用φs替换。
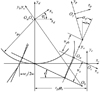 |
图7 齿条展成的直线族 |
图 7中wt是齿槽宽, 同样将矢量Ra=[0 ua 0 1]T从坐标系Sa变换到S2中, 即可得到面齿轮齿面Σ2Drac(上标Drac表示通过齿条表达的可展直纹面)的位矢方程式(15), 进一步求偏导得其单位法矢。
2.4 直线展成面齿轮齿面算例
图 8所示为根据算例1参数计算的由直线展成的面齿轮全齿高齿面Σ2Dinv相对其理论齿面Σ2的法向距离, 由齿面Σ2Dinv建立的面齿轮模型如3.2节图 11所示。最小法向距离为-5.8 μm, 位于外端齿顶, 最大法向距离为189.4 μm, 位于内端齿根, 沿0°接触线L2s(即沿内端齿顶到外端齿根的对角线)齿面Σ2Dinv相对Σ2的法向距离最小, 沿内端齿根到外端齿顶这一对角线齿面Σ2Dinv偏离Σ2的程度最大。负值法向距离表示Σ2Dinv上的点位于Σ2内部, 正值则反之。正值法向距离随内端内径L1的减小而增大, 即根切愈严重正值法向距离愈大。而在节点Lp=508 mm截面处, 法向距离极值分别为-1.4 μm和0.0 μm。
 |
图8 面齿轮可展直纹面相对理论齿面的法向距离 |
由渐开线和齿条展成的齿面Σ2Dinv, Σ2Drac是相同的, 两数值齿面之间法向距离数量级为10-6 μm。
随齿数比的变化, 在内端L1的齿根和外端L2的齿顶Σ2Dinv相对Σ2的法向距离δ1(对应内端L1的齿根)、δ2(对应外端L2齿顶)的变化如图 9所示, 随齿数比和L2的增大, 法向距离δ2逐渐趋近于0 μm, 这与2.1节的第4)点认识是一致的。由于所取内径L1小于根切条件确定的半径, 齿面偏差偏大, 但总体上未超过160 μm。由于齿数比和内径L1取值不同于算例1参数, 图 8和图 9中内端齿根法向距离略有差异。
 |
图9 可展直纹面相对理论齿面法向距离随齿数比的变化 |
据上述可知直线展成的面齿轮齿面不仅保持了很高的齿面精度, 最大法向距离不到模数的1/30。这一结论的意义在于:用可展直纹面替代面齿轮的传统理论齿面具有可行性, 从而利用直线刃刀具加工面齿轮成为了可能。进一步, 基于上述原理和下文所阐述的加工方法, 用直刃刀具单齿分度加工面只有一个运动参数, 并且对单齿来说是连续的加工方式, 即无须在齿宽方向不断停留以展成齿顶到齿根的一小片区域, 无论切齿或磨齿, 效率得到了大幅提高。再进一步将图 10所示刀具制作为直线蜗杆刀具, 有望实现单侧连续分度加工面齿轮, 但还有待进一步的研究。
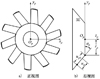 |
图10 加工面齿轮的直刃刀具 |
3 直刃刀具加工面齿轮
3.1 直刃刀具
图 10所示为基于直线展成面齿轮所用的一种直刃刀具, 该刀具的产形线为直线SL, 将该直线绕刀具轴线zp旋转, 就得到了刀具的工作锥面Σp。显然若用合金钢等材料制作刀具并在径向开制排屑槽, 可以用于切削面齿轮工件, 若在锥面上覆盖立方氮化硼等硬质材料, 可以用于磨削面齿轮工件。
直线SL的锥角为αp, 其上的固定点和动点相对坐标系Sp的关系如图 10所示, 设直线SL绕zp旋转的转角为θp, 则Σp的位矢方程可以表示为
锥面Σp的单位法矢为
3.2 直刃刀具加工面齿轮的原理及其齿面
图 11所示为用上述直刃刀具加工面齿轮的原理的示意图, 涉及6个运动, 具体为:①刀具沿y2轴的平移Cy, 其作用在于在齿宽方向排列变位变压力角直线; ②刀具沿z2轴的平移Cz, 用于提供齿高方向的变位量; ③刀具沿x2轴的平移Cx, 相当于齿轮齿条啮合时齿条的平移运动; ④刀具绕xp轴的旋转CB, 改变刀具倾角以获得不同角度的直线; ⑤面齿轮绕自身轴线z2的分度运动CA; ⑥刀具绕自身轴线zp的旋转Ωp, 用于切削工件。显然运动CA、Ωp与齿面的展成无关, 平移运动参数Cx, Cy, Cz都是CB=φs的函数。虽然采用单侧齿面和单齿分度加工, 但刀具产形面与待加工齿面是线接触, 因此效率不低。图 11与图 7和图 1所表达的运动形式虽有差异(其目的是为了简洁地表达刀具与工件的相对运动关系), 但其本质是相同的。
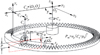 |
图11 直刃刀具加工面齿轮的原理 |
参考图 2以及可展直纹面相对理论齿面的法向距离图 8可知, 当N1=Ns时, 小轮渐开线齿面与可展直纹面的啮合极易出现线接触现象, 为此通过齿向修形将接触限制在局部十分必要。如图 11所示当令直刃刀具中心沿抛物线P运动时, 即可实现可展直纹面的齿向抛物线修形, 图中ap是抛物线修形系数, p0用于控制抛物线顶点的位置, Pm=ap(| O2Os|-p0)2(此时θs=ϕs)是该抛物线的表达式。
图 7表示了直刃刀具坐标系Sp与插齿刀坐标Ss之间的关系, 由Sp到Sc的坐标变换矩阵为
式中:αp0=αp-α; wtx=-0.5wtcos2α; uprx=up0sinα- rp·sinαp0; wty=0.5wtcosαsinα; upry=up0cosα+rpcosαp0。从Sc到Ss的坐标变换矩阵为
利用(13)式中的坐标变换矩阵M2s(此时θs=ϕs), 刀具锥面Σp在S2中的曲面族为
上标p表示直刃刀具加工的齿面, 其法矢为
联系(18)式中2个曲面参数和1个运动参数的啮合方程可以表示为
联立(18)~(20)式并应用边界条件即可求解用直刃刀具加工的面齿轮齿面Σ2p。
显然矩阵M2p=M2sMscMcp的前三阶系数矩阵L2p表达了直刃刀具在坐标系S2中的旋转, 转角变量为φs, 该矩阵第四列的第一、二、三个元素分别表达了直刃刀具在S2中的移动Cx, Cy, Cz。
4 齿面加工与TCA算例
4.1 齿面的加工
此处及下文均以算例1的参数作为齿轮副的参数。刀具参数为rp=18 mm, up0=11.23 mm, αp=45°。
图 12所示为根据(18)~(20)式计算的由直刃刀具锥面Σp展成的面齿轮工作齿面Σ2p(其宏观轮齿模型可参考图 13)相对理论齿面Σ2的法向距离。根据图 13可以说明以下问题:
 |
图12 直刃刀具加工的面齿轮齿面 |
 |
图13 面齿轮齿面与小轮齿面的啮合特性 |
1) 法向距离小:工作齿面最小法向距离仅有-85.7 μm, 不到模数的1/70, 其分布规律与图 8相似。过渡曲面的法向距离未示出, 其最小距离为-323.6 μm, 约是模数的1/20, 但过渡曲面不参与齿轮的啮合, 对啮合性能无影响。所有法向距离均为负值, 说明Σ2p与Σ1的啮合不存在干涉问题。
2) Σ2p与Σ2Dinv(Σ2Drac)不同:图 8所示Σ2Dinv(Σ2Drac)相对Σ2的法向距离有正有负, 但图 12所示法向距离全为负值, 说明Σ2p不同于Σ2Dinv(Σ2Drac)。由于Σ2Dinv(Σ2Drac)直接由包络渐开线的平面直线族沿齿宽排列而成, 该直线族与渐开线均相切, 但不要求直线移动速度与法矢垂直; 对于Σ2p, 要求锥面Σp移动速度须垂直于其法矢, 须满足(20)式。
3) 存在根切:随面齿轮内径的减小, 齿面Σ2Dinv(Σ2Drac)偏离Σ2的程度越来越大, 并受刀具参数的影响。例如当进一步增大刀具的半径rp后, 图 12内端齿根部的最小法向距离将进一步减小, 根切导致求解结果发散。因此需要根据根切, 合理设计刀具参数, 若保持内端根部相同, 则刀具半径和锥角的取值是此消彼长的关系。限于篇幅, 本文对此问题不做进一步的展开。
另外对于直刃刀具展成的面齿轮齿面, 齿数比对齿面法向距离的影响与图 9类似, 亦不再赘述。
4.2 TCA结果
齿面接触分析算法和所用坐标系与文献[1]中第17章的相同。当无齿向修形齿面Σ2p与小轮渐开线齿面Σ1啮合时, 同一转角下接触点不唯一, 并呈现发散的接触路径, 为避免误解未示出其结果。
面齿轮齿向修形齿面Σ2p与小轮齿面Σ1啮合的几何接触特性如图 13所示, 其中图 13a)至13b)中的齿向修形系数为:ap=0.000 45, p0=-12 mm, 其目的是将接触路径限制在节点P附件, 以便与Σ2的接触特性比较; 图 13c)至13d)中ap=0.000 45, p0=-2 mm, 以将接触路径限制在齿宽中间并获得连续传动误差。
由图 13, 可以看出:①通过齿向修形和选取不同的抛物线顶点参数, 可以将接触路径限制在不同的齿向位置从而获得局部接触, 图示接触线端点到齿面的法向距离小于0.006 35 mm。为进一步降低对安装误差的敏感性, 可以增大ap。②将接触路径限制在齿廓方向, 产生了抛物线几何传动误差; 当接触路径趋于齿宽的中央时, 传动误差逐渐变为对称的抛物线; 总体上外端传动误差的幅值小于内端传动误差的幅值。结合图 12可知, 齿面Σ2p与Σ1在齿廓方向是局部共轭的。
图 13a)的接触路径与理论齿面的接触路径(Ns-N1=1~3)几乎相同, 但前者呈现出传动误差(见图 13b)), 后者传动误差一般为0, 为减振降噪, 后者通常需要齿廓抛物线修形以预置抛物线传动误差[2], 即类似于图 13c),13d)所示路径和传动误差。
综上Σ2p与Σ1的啮合呈现的特性是:齿廓方向是局部共轭的, 齿宽方向须修形以将接触限制在局部, 因此利用齿面主动设计[15]等方法进一步预控其啮合性能的空间巨大。面齿轮齿向修形可展直纹面的几何啮合性能与理论齿面的几何啮合性能相当。
5 结论
1) 基于传统的插齿方法,建立面齿轮齿面,在该齿面上建立了空间直线的方程,基于数值计算,说明了面齿轮齿面可以视为空间变压力角变位直线族。
2) 根据面齿轮与小轮的啮合,阐述了渐开线与变位变压力角直线的啮合过程,并对啮合的几何关系进行了说明,建立了面齿轮可展直纹面,数值计算表明,在齿数比较大时,用可展指纹面替代面齿轮理论齿面具有可行性,并带来加工优势。
3) 根据面齿轮可展直纹面这一结论,提出了一种直刃刀具加工面齿轮的方法,设计了直刃刀具,阐述了直刃刀具加工面齿轮的原理,建立了直刃刀具加工面齿轮的齿面位矢方程,数值计算表明相对传统插齿法的齿面,齿面法向距离属于微观量,并且刀具与待加工齿面是线接触的,凸显出这种方法高效较准确加工面齿轮的重要意义。
4) 对直刃刀具加工的齿面和小轮标准渐开线齿面的啮合进行了齿面接触分析,通过适当的齿向修形可以将接触限制在局部,并可获得较理想的几何啮合性能。但未来为获得更好的几何啮合性能,应用齿面局部综合法、齿面差曲面主动设计法,有望进一步优化其几何啮合性能甚至承载性能。
References
- Faydor L L. Gear Geometry and Applied Theory[M]. Englewood Cliffs: PTR Prentice Hall, 1994 [Google Scholar]
- Faydor L L, Alfonso F, Llaudio Z, et al. Design, Generation, and Stress Analysis of Two Version of Geometry of Face Gear Drives[J]. Mechanism and Machine Theory, 2002, 37 (5): 1179– 1211 [Article] [CrossRef] [Google Scholar]
- Guo Hui, Zhao Ning, Zhang Shuyan. Envelope Residuals Research of Face Gear Based on Disc Grinding Wheel Tooth Grinding[J]. Journal of Aerospace Power, 2014, 29 (11): 2743– 2750 [Article] (in Chinese) [Google Scholar]
- Wang Yanzhong, Zhao Hongpu, Lan Zhou, et al. Method of Face Gear Grinding-Honing Machining Based on Aviation Environment[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42 (4): 646– 653 [Article] (in Chinese) [Google Scholar]
- Hermann J S. Coniface Face Gear Cutting and Grinding[J]. Gear Solutions, 2010, 18 (9): 39– 47 [Article] [Google Scholar]
- David J F, Adrian R, George F, et al. Apparatus for Manufacturing a Face Gear[P]. United States: US2008/0268750A1 [Google Scholar]
- Kubo A, Ueda A. Gear Geometry as a Function of the Production Method[J]. Mechanisms and Machine Science, 2017, 51 (4): 27– 44 [Article] [CrossRef] [Google Scholar]
- Yang Xiaoyu, Tang Jinyuan. Research on Manufacturing Method of CNC Plunge Milling for Spur Face-Gear[J]. Journal of Materials Processing Technology, 2014, 214 (8): 3013– 3019 [Article] [CrossRef] [Google Scholar]
- Tang Jinyuan, Yang Xiaoyu. Research on Manufacturing Method of Planing for Spur Face-Gear with 4-Axis CNC Planer[J]. Int J Adv Manuf Technol, 2016, 82 (3): 847– 858 [Article] [CrossRef] [Google Scholar]
- Hermann J S. Method and Tool for Manufacturing Face Gear[P]. United States, US2012/0099939A1 [Google Scholar]
- Hermann J S. Continuous Method for Manufacturing Face Gears[P]. Europenan: Ep2528705B1 [Google Scholar]
- Mao Shimin, Zeng Xinyu. A Method for Face Gear Grinding[P]. China: CN103264198 A (in Chinese) [Google Scholar]
- Peng Xianlong, Niu Qinyu, Guo Wei, et al. A New Method of Motion Rule Synthesis for Face Gear Manufacturing by Plane-Cutter[J]. Journal of Mechanical Design, 2018, 140 (4): 023302 [Article] [CrossRef] [Google Scholar]
- Guo Hui. Research on Method of Hobbing Face-Gear and Gearing Performance[D]. Xi'an: Northwestern Polytechnical University, 2009 (in Chinese) [Google Scholar]
- Mu Yanming, Li Wenli, Fang Zongde. Tooth Surface Modification Method of Face-Milling Spiral Bevel Gears with High Contact Ratio Based on Cutter Blade Profile Correction[J]. The International Journal of Advanced Manufacturing Technology, 2020, 106 (2): 3229– 3237 [Article] [CrossRef] [Google Scholar]
All Figures
 |
图1 面齿轮2与插齿刀s或小轮1的啮合 |
| In the text | |
 |
图2 面齿轮齿面上的直线族cj |
| In the text | |
 |
图3 面齿轮齿面上的齿廓曲线与直线的法向距离 |
| In the text | |
 |
图4 面齿轮齿面上直线相对坐标轴的方向角 |
| In the text | |
 |
图5 渐开线与面齿轮齿面接触的轨迹 |
| In the text | |
 |
图6 渐开线与变位变压力角直线 |
| In the text | |
 |
图7 齿条展成的直线族 |
| In the text | |
 |
图8 面齿轮可展直纹面相对理论齿面的法向距离 |
| In the text | |
 |
图9 可展直纹面相对理论齿面法向距离随齿数比的变化 |
| In the text | |
 |
图10 加工面齿轮的直刃刀具 |
| In the text | |
 |
图11 直刃刀具加工面齿轮的原理 |
| In the text | |
 |
图12 直刃刀具加工的面齿轮齿面 |
| In the text | |
 |
图13 面齿轮齿面与小轮齿面的啮合特性 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


