Simulation and Analysis on Tooth Meshing Ease-Off Surface of Gears Based on Polynomial Topology Modification

Bingyang Wei; Xuemei Cao; Xiaozhong Deng

doi:10.1051/jnwpu/20203840897

All issues

Volume 38 / No 4 (August 2020)

JNWPU, 38 4 (2020) 897-903

Full HTML

Open Access

Issue		JNWPU Volume 38, Number 4, August 2020


Page(s)		897 - 903
DOI		https://doi.org/10.1051/jnwpu/20203840897
Published online		06 October 2020

JNWPU 2020, 38(4): 897-903

Simulation and Analysis on Tooth Meshing Ease-Off Surface of Gears Based on Polynomial Topology Modification

基于多项式拓扑修形的差齿面啮合仿真与解析

Bingyang Wei (魏冰阳)¹, Xuemei Cao (曹雪梅)¹ and Xiaozhong Deng (邓效忠)¹^,2

¹ School of Mechanical & Electronical Engineering, Henan University of Science & Technology, Luoyang 471003, China
² Collaborative Innovation Center of Machinery Equipment Advanced Manufacturing of Henan Province, Luoyang 471003, China

Received: 20 September 2019

Abstract

Based on the principles of common-generating conjugation mapping of pinion-rank-gear meshing, the constructing of ease-off surface has been done by means of the topology modification of the 4-order polynomial surface. The simulation method of tooth surface mesh is purposed based on the ease-off surface. By analyzing topological structure characteristics of ease-off surface such as modification gradient curves, contact line-off and contact path-off, the meshing characteristics such as the contact area, the contact line and transmission error are determined. It is stated on the interaction relations of coefficients of the 4-order polynomial to the topological construction of surface. The methods for reconstruction and analysis of ease-off surface with considering axis misalignments are presented by the direct transformation of coordinate systems. Taking the topological construction of four kinds of surfaces as examples, characteristics parameters such as modification gradient of tooth surface, contact path and transmission errors are simulated. They are expounded on the corresponding parameters of controlling form and adjusting methods for tooth surface. These methods take goals of adjusting-modification and controlling-property for tooth surface mesh. It is improved and developed the meshing analysis method of ease-off surface of tooth. The presented method is liable to provide the basis data for the further loaded contact analysis of complicated tooth surface and the more direct technical for the 3-D topological optimization of tooth surface.

摘要

基于齿条产成圆柱齿轮时的等切共轭映射原理，采用四阶多项式曲面修形构造ease-off差齿面；提出基于ease-off差齿面的啮合仿真方法，通过解析ease-off差齿面的拓扑结构：修形梯度、差曲线、差程线等特征要素，获取了齿面接触区、接触线、传动误差等轮齿啮合特性，阐述了四阶多项式系数与齿面拓扑结构之间的耦合关系。利用坐标变换，给出了考虑错位量的ease-off曲面分析重构方法。以4种曲面拓扑形式为例，对齿面修形梯度、接触路径、传动误差等性能参数进行了模拟仿真，给出了相应的控形参数与控制方法，达到了对齿面几何控形控性的目的。完善并发展了ease-off差齿面啮合分析方法，为复杂齿面承载接触LTCA、拓扑优化，提供了更加便利有效的手段。

Key words: rank generating / tooth contact analysis / modification control / axis misalignments / simulation

关键字 : 齿条产形 / 轮齿接触分析 / 控形 / 错位量 / 仿真

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

齿轮啮合仿真已成为齿轮传动设计与分析必不可少的手段。20世纪90年代, 随着计算机技术的发展, 轮齿接触分析TCA(tooth contact analysis)技术在复杂齿面的设计方面得到了应用[1-2]。借助TCA技术, 文献[1-5]发展了“局部综合”法与齿面主动设计, 实现了齿面接触印痕与传动误差的预控。文献[6]给出了TCA的改进算法, 使TCA的求解方法得到了一定程度的简化。文献[7]提出了TCA的分解算法, 统一了轮齿齿面接触和边缘接触分析数学模型, 基于完全共轭齿面, 分离传动误差, 仅需要求解2个非线性方程组, 极大地降低了求解难度。文献[8-9]发展了一种更适宜数值计算的ease-off差齿面仿真方法。文献[10-11]利用ease-off拓扑, 解决了弧齿锥齿轮高阶传动误差齿面拓扑、直齿锥齿轮低安装误差敏感性设计与预控的问题。文献[12-13]发展了ease-off等距变换方法, 据此提出了曲面综合弧齿锥齿轮加工参数计算新方法。利用TCA、ease-off曲面拓扑, 文献[14]研究了高阶传动误差斜齿轮修形的设计与加工实现方法, 文献[15]研究了双重螺旋法加工参数对齿面特征的影响规律。但这些研究对ease-off曲面的拓扑映射、啮合信息挖掘尚存在不足。鉴于此, 本文基于齿条-圆柱齿轮等切共轭映射原理, 提出了一种四阶多项式拓扑修形、ease-off差齿面的构建方法, 给出了差曲线、接触路径、传动误差等齿面性能参数的解析方法, 以期更便利地完成轮齿啮合仿真; 通过ease-off差齿面的设计, 实现了复杂齿面“形-性”的主动控制。

1 齿条产形与ease-off曲面构建

2 圆柱齿轮的齿条产成多项式曲面方程

齿条产形面用于展成被加工齿面, 用四次多项式表达

(1) 式完整表达式为15项, 取其中的7项, 作为齿条拓扑面(u为纵向，v为齿廓方向), 则可以构建一个双峰抛物面

式中:系数a₀₂, a₀₄用于控制v方向曲面的形状; a₂₀, a₄₀用于控制u方向曲面的形状; a₁₁, a₂₂用于控制曲面的扭转程度与方向。

当把(2)式作为齿条面时, O₀点作为齿条产成圆柱齿轮的节点。利用矢量旋转变换, 绕x₀旋转α(压力角), 绕y₀旋转β(螺旋角), 在S₀坐标系(见图1), 斜齿条方程如下所示：

建立齿条与圆柱齿轮产成加工坐标系, S₀齿条坐标系, S_d固定坐标系, S₁齿轮坐标系, 如图2所示。通过求解齿条与齿面啮合方程可得圆柱齿轮啮合转角

式中：r₁为展成齿轮的节圆半径；法矢n₀分量n_y, n_z可由(2)、(3)式确定。

通过坐标变换可求出圆柱齿轮位矢方程与法矢

式中, M_1d为S_d到S₁的坐标变换矩阵。

当(2)式取为平面时得到标准渐开线圆柱齿轮方程r_s(u, v); 取不同的控形参数, 则得到不同拓扑修形齿面r₁(u, v)。

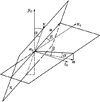图1

齿条面坐标系

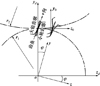图2

齿面产成坐标系

3 差曲面ease-off的构建方法

标准渐开线齿面Σ_s与修形齿面Σ_i(i=1, 2代表小轮与大轮)两曲面对应点法向的分离误差(修形梯度量)为

修形齿面Σ_i和标准渐开线齿面Σ_s映射为差曲面ease-off_(i), 如图3所示。

因齿条平面Σ₀左右两侧分别与小轮Σ₁、大轮Σ₂相切, 三者互为等切共轭啮合关系(图2), Σ₁-Σ₀-Σ₂三者是一一映射的。以齿条平面Σ₀为坐标平面(u, v)做映射, 绘制网格点的离差z_d, 可构建ease-off₍₁₎与ease-off₍₂₎的等距映射。由于等切共轭关系对应点可直接做代数和

即可得到大、小轮共轭差齿面ease-off(见图4)。

基于等切共轭原理构建ease-off曲面, 无需求解小、大轮之间的共轭啮合方程, 就可建立啮合场与投影面之间的等距映射关系。在接触线方向ease-off曲面法曲率直接表示了齿面接触点的差曲率。

图3

ease-off曲面映射关系

图4

差齿面ease-off

4 差齿面ease-off啮合仿真信息解析

根据原TCA方法, 已不足以表达ease-off三维曲面拓扑特征, 因此引入等差线、差曲线、差程线等一些新的概念。

5 等差线与修形梯度

(7) 式表示的为图4中的网格节点, 把其拟合为(1)式所示的二元四次多项式

该式对ease-off曲面拟合精度达到了10^-6 mm, 可以满足齿面啮合仿真的要求。对ease-off曲面的分析, 可以通过对(8)式的解析得到。

差齿面ease-off直观呈现了齿面修形梯度(见图5)。当给定曲面ease-off上z_n某一值时, 则由(8)式可求得相等修形量的线——等差线

工程上通常认为齿轮滚检的涂色层厚度为3~6 μm, 其相应的等差线包围区域(图4、5椭圆区域)代表了齿面接触斑点。同时, 可用于预测承载下接触应力/应变在齿面发展趋势。

图5

ease-off修形梯度图

6 差曲线与差程线

1) 差曲线瀑布图

由(3)式可以知道, 任意一个转角φ_i值, 对应一系列(u_i, v_i)值, 代入(8)式可得到一系列z_di, 它代表了ease-off曲面上一条瞬时接触线s, 如图6所示。

它反映了齿面修形后由线接触转变为点接触的特征, 简称差曲线。差曲线切方向即瞬时接触椭圆长轴方向。差曲线通常为抛物线型, 其对应的差曲率k_s, 接触线方向角θ可由du/dv比值求出

重复上述过程可以得到若干差曲线序列形成的曲线簇, 表示为

式中:j为代表瞬时共轭线序列；i为代表线上点的序列。

把(10)式中一系列的差曲线最低点与投影面相切, 可绘制出如图6所示的差曲线瀑布图。差曲线瀑布图能够清晰地反映瞬时接触点与接触路径方向, 直观呈现任意接触线的差曲率。

2) 差程线与传动误差

(10) 式中抛物线的最低点代表了齿面啮合过程中的一个瞬时接触点, 一系列瞬时接触点构成了ease-off曲面上一条曲线——差程线

它代表了啮合线的差程量, 投影到齿面就是接触路径, 接触路径方向角σ可由du/dv比值表示。差程线通常也呈抛物线型, 设其弧长参数为t, 法曲率k_t, 则

转化为角度量Δφ₂表示, 即为传动误差TE(transmission errors, 单位:μrad):

式中, r为对应点的回转半径。

图7中给出了3幅传动误差, 代表相邻三齿交替啮合的过程[3]。

3) 瞬时接触椭圆参数

对于任意接触点, 由于已知了2个方向的差曲率:接触线方向k_s、接触路径方向k_t(图8), 则可由欧拉公式计算出瞬时接触椭圆短轴方向的差曲率

如果已知载荷承担比, 可以计算出任意瞬时接触应力及变形的大小。

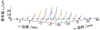图6

差曲线瀑布图

图7

二阶抛物线传动误差

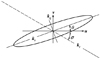图8

瞬时接触椭圆参数

7 多项式曲面拓扑的控形控性

本文选取4种情况对ease-off曲面进行分析, 4种曲面类型如表 1所示。

表1

曲面控形参数

齿轮参数:大小轮齿数z₂=62, z₁=21, 法向压力角α=20°, 螺旋角β=13°, 法向模数m_n=5 mm, 齿宽B=80 mm, 法向变位系数x_n1=0.3, x_n2=0.12。

8 二阶抛物面拓扑

齿轮齿向与齿廓为二阶抛物面修形, 其控形参数为a₀₂, a₂₀。齿面接触斑点按齿廓、齿宽占比80%设计, 控形参数取值为

齿廓方向: 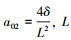为齿高

齿长方向: 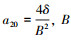为齿长

根据需要, 可以把总的修形量δ分配到2个齿面, 取

计算后获得ease-off曲面如图4所示, 椭圆表示了齿面接触仿真斑点的形状与大小, 满足齿长、齿宽的占比70%~80%的要求。进一步解析出等差线梯度、差曲率瀑布图、传动误差如图5至7所示。

9 扭转抛物面拓扑

扭转抛物面拓扑在齿面上将产生对角修形的效果。3个系数a₀₂, a₁₁, a₂₀在控形上存在一定的耦合作用, a₁₁主控ease-off曲面对角扭转量、差程量, 取

获得的ease-off曲面如图9所示, 用色差梯度表示。其形态明显呈现对角修形的效果, 传动误差仍然保持二阶抛物线型(见图10)。

与对称抛物面相比, 对角修形是一种更先进的齿面修形方式, 它能够更加灵活地控制接触路径、接触线、传动误差等几何特性, 对改善齿轮动态啮合性能有利[16]。

图9

对角修形ease-off

图10

对角修形传动误差

10 四阶抛物面拓扑

齿轮齿向、齿廓2个方向都采用四次抛物线修形。(2)式中控形系数a₀₄, a₂₂, a₄₀取

ease-off曲面结构如图11所示, 修形后齿面中部差曲率比二阶小, 靠近齿面边界陡峭, 类似于在抛物线修形基础上附加了修缘。接触区扩展呈长方形, 外部修形梯度急剧扩大。传动误差(见图12)呈平顶形状。四阶抛物线修形对于保持齿面接触刚度、低传动误差与低误差敏感性有利[17-18]。

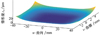图11

四阶抛物面ease-off

图12

四阶平顶传动误差

11 四阶双峰抛物面拓扑

与平顶四次抛物线修形相比, 进一步发展四次双峰抛物线修形[18], 称为高级运动误差曲线[17]。

齿廓控形参数:a₀=6.21×10^-4, a₀₂=-4.79×10^-4, a₀₄=2.29×10^-5。a₀₂控制双峰中凹量的大小, a₀₄控制抛物线的陡峭程度。

齿长方向为二次抛物线修形, 控形参数:a₂₀=3.04×10^-6。

双峰抛物面修形ease-off曲面结构呈8字型(见图13), 传动误差曲线少量中凹(见图14), 与预期的高阶运动误差曲线效果一致[17-18]。

图13

四阶双峰ease-off曲面

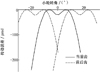图14

双峰传动误差

12 考虑错位量的ease-off曲面分析

把轴线(图2的x坐标)位错量用相对于齿面中点的角度、线性偏移量表示:水平面-x_do_dy_d(χ, Δa)、垂直面-x_do_dz_d(ψ, Δb)。任何方向的错位量都可以分解到水平、垂直2个方向。齿面错位可以认为齿条向相反方向错位, 这样可以直接使用前述ease-off曲面数值, 而无需分别计算大小轮坐标位错。据(2)式的变换矩阵, 把ease-off曲面(u, v, z_d)转化到齿条坐标系S₀

再计算错位引起的齿条误差(x′, y′, z′)

式中变换矩阵

最后, 把齿条坐标误差变换回ease-off曲面

式中, T^-1(α, β)为T(α, β)逆矩阵。

取(χ=0.002°, Δa=0.5 mm), (ψ=0.003°, Δb=10 mm), 计算图4错位下ease-off曲面的变化, 结果如图15所示。与图4对比, 接触位置向右端和齿顶偏移。由此可判断齿面接触状况对轴线错位的敏感性。

除了上面所述的4种结构, 根据(1)式还可以派生出更多拓扑形式。例如, 二次-四次复合、分段曲面拓扑等。这些拓扑形式由数值化齿面表达可直接用于其他三维软件动力学仿真分析, 在高精度万能型磨齿机上实现加工[14, 16]。

图15

轴线错位下ease-off曲面

13 结论

提出了一种齿条-齿轮等切共轭、多项式拓扑修形与ease-off差齿面的仿真方法, 给出了齿面啮合信息解析, 轴线错位的ease-off曲面分析方法。

利用四阶多项式拓扑, 能够准确控制齿面微分结构、修形梯度, 实现复杂齿面的拓扑重构、接触性能分析; 对齿面拓扑达到控形控性的目的, 避免了常规控形方法单一、曲面缝合问题。

以齿条为等切共轭面, 能够形成ease-off曲面与齿面啮合场的等距映射关系, 准确反映轮齿啮合信息, 快速解析轮齿性能参数:差曲线、接触路径、传动误差、瞬时接触椭圆等, 避免了常规ease-off曲面啮合信息映射失真、畸变。本文方法简捷, 易于数值计算, 解析数据可直接用于承载接触分析LTCA, 为轮齿动态啮合性能仿真奠定了基础。

References

LITVIN F L, FUENTES A. Gear Geometry and Applied Theory[M]. New York: Cambridge University Press, 2004 [Google Scholar]
LITVIN F L. Computerized Design, Simulation of Meshing, and Contact and Stress Analysis of Face-Milled Formate Generated Spiral Bevel Gears[J]. Mechanism and Machine Theory, 2002, 37 (5): 441– 459 [Article] [CrossRef] [Google Scholar]
FANG Zongde, LIU Tao, DENG Xiaozhong. Tooth Contact Analysis of Spiral Bevel Gears Based on the Design of Transmission Error[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23 (3): 226– 230 [Article] (in Chinese) [Google Scholar]
CAO Xuemei, ZHANG Hua, FANG Zongde. Design and Analysis of Laoded Transmission Errors for Aviation Spiral Bevel Gears[J]. Journal of Aerospace Power, 2009, 24 (11): 2618– 2624 [Article] (in Chinese) [Google Scholar]
CAO Xuemei, FANG Zongde, XU Hao. Function-Oriented Active Tooth Surface Design of Spiral Bevel Gears and Experimental Tests[J]. Chinese Journal of Mechanical Engineering, 2008, 44 (7): 209– 214 [Article] (in Chinese) [Google Scholar]
TANG Jinyuan, Lu Yanfeng, ZHOU Chao. Research on Improved Tooth Contact Analysis Algorithm of Spiral Bevel Gears[J]. Journal of Aerospace Power, 2009, 24 (1): 189– 195 [Article] (in Chinese) [Google Scholar]
CAO Xuemei, YANG Bohui, DENG Xiaozhong. Novel Decomposition Methodology for Tooth Contact Analysis and Experiment Tests[J]. Journal of Mechanical Engineering, 2018, 54 (5): 47– 52 [Article] (in Chinese) [Google Scholar]
HERMANN J S. What "Ease-off" Shows about Bevel and Hypoid Gears[J]. Gear Technology, 2001, (9/10): 18– 23 [Article] [Google Scholar]
CHEN Shuhan, YAN Hongzhi, MING Xingzu, et al. Difference Surface Model Establishment and Simulation in Spiral Bevel Gear[J]. Journal of System Simulation, 2009, 21 (11): 3430– 3433 [Article] (in Chinese) [Google Scholar]
CAO Xuemei, DENG Xiaozhong, NIE Shaowu. Ease-Off Flank Topography Design for Aviation Spiral Bevel Gears with Higher-Order Transmission Errors by Modification of Conjugate[J]. Journal of Aerospace Power, 2015, 30 (1): 195– 200 [Article] (in Chinese) [Google Scholar]
CAO Xuemei, SUN Ning, DENG Xiaozhong. Design for Straight Bevel Gear Based on Low Installation Error Sensitivity and Experiment Tests[J]. Journal of Aerospace Power, 2016, 31 (1): 227– 232 [Article] (in Chinese) [Google Scholar]
WEI Bingyang, DENG Xiaozhong, TONG Angxin, et al. Surface Synthesis Method on Generating Parameters Computation of Spiral Bevel-Gears[J]. Journal of Mechanical Engineering, 2016, 52 (1): 20– 25 [Article] (in Chinese) [Google Scholar]
WEI Bingyang, YANG Jianjun, TONG Angxin. Tooth Meshing Simulation and Analysis Based on Isometric Mapping Ease-Off Surface[J]. Journal of Aerospace Power, 2017, 32 (5): 1259– 1265 [Article] (in Chinese) [Google Scholar]
JIANG Jinke, FANG Zongde, SU Jinzhan. Design and Grinding for Modified Helical Gears with a Higher-Order Transmission Error[J]. Journal of Harbin Institute of Technology, 2014, 46 (9): 43– 49 [Article] (in Chinese) [Google Scholar]
ZHANG Yu, Yan Hongzhi, Zeng Tao, et al. Influence Regularity of Helical Movement and Cutter Parameters on the Generated Tooth Surface Characteristic of Duplex Helical Method[J]. Journal of Mechanical Engineering, 2018, 54 (5): 53– 61 [Article] (in Chinese) [CrossRef] [Google Scholar]
JIANG Jinke, FANG Zongde, JIA Haitao. Research on Design and CNC Grinding Machine for Diagonal Modified Helical Gearxy1 Journal of Mechanical Engineering, 2014, 50 (19): 158– 165 [Article] (in Chinese) [CrossRef] [Google Scholar]
Stadtfeld H J. The Ultimate Motion Graph[J]. ASM E J of Mechanical Design, 2000, 122 (3): 317– 322 [CrossRef] [Google Scholar]
WEI Bingyang, FANG Zongde, ZHOU Yanwei, et al. On Improving Design of Spiral Bevel Gear with Higher-Order Transmission Error Curvexy1 Journal of Northwestern Polytechnical University, 2003, 21 (6): 757– 760 [Article] (in Chinese) [Google Scholar]

All Tables

表1

曲面控形参数

In the text

All Figures

	图1 齿条面坐标系
In the text

	图2 齿面产成坐标系
In the text

	图3 ease-off曲面映射关系
In the text

	图4 差齿面ease-off
In the text

	图5 ease-off修形梯度图
In the text

	图6 差曲线瀑布图
In the text

	图7 二阶抛物线传动误差
In the text

	图8 瞬时接触椭圆参数
In the text

	图9 对角修形ease-off
In the text

	图10 对角修形传动误差
In the text

	图11 四阶抛物面ease-off
In the text

	图12 四阶平顶传动误差
In the text

	图13 四阶双峰ease-off曲面
In the text

	图14 双峰传动误差
In the text

	图15 轴线错位下ease-off曲面
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] LITVIN F L, FUENTES A. Gear Geometry and Applied Theory[M]. New York: Cambridge University Press, 2004 [Google Scholar]

[2] LITVIN F L. Computerized Design, Simulation of Meshing, and Contact and Stress Analysis of Face-Milled Formate Generated Spiral Bevel Gears[J]. Mechanism and Machine Theory, 2002, 37 (5): 441– 459 [Article] [CrossRef] [Google Scholar]

[3] FANG Zongde, LIU Tao, DENG Xiaozhong. Tooth Contact Analysis of Spiral Bevel Gears Based on the Design of Transmission Error[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23 (3): 226– 230 [Article] (in Chinese) [Google Scholar]

[4] CAO Xuemei, ZHANG Hua, FANG Zongde. Design and Analysis of Laoded Transmission Errors for Aviation Spiral Bevel Gears[J]. Journal of Aerospace Power, 2009, 24 (11): 2618– 2624 [Article] (in Chinese) [Google Scholar]

[5] CAO Xuemei, FANG Zongde, XU Hao. Function-Oriented Active Tooth Surface Design of Spiral Bevel Gears and Experimental Tests[J]. Chinese Journal of Mechanical Engineering, 2008, 44 (7): 209– 214 [Article] (in Chinese) [Google Scholar]

[6] TANG Jinyuan, Lu Yanfeng, ZHOU Chao. Research on Improved Tooth Contact Analysis Algorithm of Spiral Bevel Gears[J]. Journal of Aerospace Power, 2009, 24 (1): 189– 195 [Article] (in Chinese) [Google Scholar]

[7] CAO Xuemei, YANG Bohui, DENG Xiaozhong. Novel Decomposition Methodology for Tooth Contact Analysis and Experiment Tests[J]. Journal of Mechanical Engineering, 2018, 54 (5): 47– 52 [Article] (in Chinese) [Google Scholar]

[8] HERMANN J S. What "Ease-off" Shows about Bevel and Hypoid Gears[J]. Gear Technology, 2001, (9/10): 18– 23 [Article] [Google Scholar]

[9] CHEN Shuhan, YAN Hongzhi, MING Xingzu, et al. Difference Surface Model Establishment and Simulation in Spiral Bevel Gear[J]. Journal of System Simulation, 2009, 21 (11): 3430– 3433 [Article] (in Chinese) [Google Scholar]

[10] CAO Xuemei, DENG Xiaozhong, NIE Shaowu. Ease-Off Flank Topography Design for Aviation Spiral Bevel Gears with Higher-Order Transmission Errors by Modification of Conjugate[J]. Journal of Aerospace Power, 2015, 30 (1): 195– 200 [Article] (in Chinese) [Google Scholar]

[11] CAO Xuemei, SUN Ning, DENG Xiaozhong. Design for Straight Bevel Gear Based on Low Installation Error Sensitivity and Experiment Tests[J]. Journal of Aerospace Power, 2016, 31 (1): 227– 232 [Article] (in Chinese) [Google Scholar]

[12] WEI Bingyang, DENG Xiaozhong, TONG Angxin, et al. Surface Synthesis Method on Generating Parameters Computation of Spiral Bevel-Gears[J]. Journal of Mechanical Engineering, 2016, 52 (1): 20– 25 [Article] (in Chinese) [Google Scholar]

[13] WEI Bingyang, YANG Jianjun, TONG Angxin. Tooth Meshing Simulation and Analysis Based on Isometric Mapping Ease-Off Surface[J]. Journal of Aerospace Power, 2017, 32 (5): 1259– 1265 [Article] (in Chinese) [Google Scholar]

[14] JIANG Jinke, FANG Zongde, SU Jinzhan. Design and Grinding for Modified Helical Gears with a Higher-Order Transmission Error[J]. Journal of Harbin Institute of Technology, 2014, 46 (9): 43– 49 [Article] (in Chinese) [Google Scholar]

[15] ZHANG Yu, Yan Hongzhi, Zeng Tao, et al. Influence Regularity of Helical Movement and Cutter Parameters on the Generated Tooth Surface Characteristic of Duplex Helical Method[J]. Journal of Mechanical Engineering, 2018, 54 (5): 53– 61 [Article] (in Chinese) [CrossRef] [Google Scholar]

[16] JIANG Jinke, FANG Zongde, JIA Haitao. Research on Design and CNC Grinding Machine for Diagonal Modified Helical Gearxy1 Journal of Mechanical Engineering, 2014, 50 (19): 158– 165 [Article] (in Chinese) [CrossRef] [Google Scholar]

[17] Stadtfeld H J. The Ultimate Motion Graph[J]. ASM E J of Mechanical Design, 2000, 122 (3): 317– 322 [CrossRef] [Google Scholar]

[18] WEI Bingyang, FANG Zongde, ZHOU Yanwei, et al. On Improving Design of Spiral Bevel Gear with Higher-Order Transmission Error Curvexy1 Journal of Northwestern Polytechnical University, 2003, 21 (6): 757– 760 [Article] (in Chinese) [Google Scholar]