| Issue |
JNWPU
Volume 38, Number 4, August 2020
|
|
|---|---|---|
| Page(s) | 889 - 896 | |
| DOI | https://doi.org/10.1051/jnwpu/20203840889 | |
| Published online | 06 October 2020 | |
Open-Hole 3D Braided Composites Strength Prediction and Stress Analysis
开孔三维编织复合材料强度预测及应力分析
1
College of Mechanical Engineering, Donghua University, Shanghai 201620, China
2
College of Textiles, Donghua University, Shanghai 201620, China
3
College of Textile and Clothing, Xin Jiang University, Urumchi 830000, China
4
Department of Material Engineering, University of British Columbia, Vancouver V6 T1 Z4, Canada
Received:
20
October
2019
The stress concentration caused by notches is a common engineering issue for composite structure application. 3D braided composite possess excellent damage tolerance compared to common laminates. The tensile properties of 3D braided composite with open-hole and un-notched were experimentally examined. The mechanic properties of 3D braided composite in other directions are predicted using FGM (Fabric Geometry Model) and finite element analysis. The stress distributions around the hole and perpendicular to the loading direction are analyzed based on Abaqus software. The simulation results were compared with Lekhnitskii's analytical study. The open-hole strength of 3D braided composite was predicted respectively using Average stress failure criteria, Point stress failure criteria (PSC), and also the progressive failure analysis based on different failure criteria. The predicted strength results were compared to the experimental values. The results show the PSC predicted strength matched the experiment, while the progressive failure analysis can predict the failure initiation, propagation and final failure mode.
摘要
由缺陷引起的应力集中是复合材料结构件使用时需要考虑的工程问题。三维编织复合材料相对于传统复合材料具有优异的损伤容限性能。首先对含缺陷前后三维(3D)编织复合材料的拉伸性能进行试验研究,并通过FGM(fabric geometry model)对其他方向材料性能进行预测。然后基于Abaqus有限元对开孔后孔周边应力分布进行分析,并和Lekhnitskii理论进行了对比,同时对沿孔垂直于在载荷方向应力分布进行了观察。分别基于传统平均应力准则和点应力准则以及基于不同失效准则的渐进失效理论对含开孔三维编织复合材料强度进行预测,并与试验结果进行了对比。结果表明,点应力准则可以很好的预测3D编织复合材料含缺陷拉伸强度,而渐进失效分析可以模拟拉伸过程中的损伤起始,损伤扩展和最终破坏模式。
Key words: 3D braided composite / open-hole / strength prediction / progressive failure / stress / simulation / FGM
关键字 : 三维编织 / 开孔 / 强度预测 / 渐进失效 / 应力
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
三维(3D)编织复合材料具有优异的损伤容限性能、冲击性能、抗分层以及结构一体化成型等优点,在复合材料领域具有广泛应用前景。
Camponeschi和Macander等[1-2]首先对不同编织工艺对复合材料力学性能进行了研究,发现采用3×1编织工艺时时,3D编织复合材料具有最优的拉伸性能,同时发现切边效应对三维编织复合材料力学性能影响极大。Gause等[3]对三维编织复合材料的损伤容限性能进行了评估,发现含开孔时,三维编织复合材料可以保留最高的剩余强度,该发现使得三维编织复合材料得到了极大关注。Ko[4-5]首次提出三维编织复合材料单胞模型以及FGM对材料的力学性能进行预测, 使得三维编织复合材料的数值预测成为可能。Xu、Fang和Zhang等[6-8]基于有限元采用单胞模型对三维编织复合材料进行了均质化分析。Sun等[9]通过数字单元方法对三维编织复合材料材料性能进行预测。Carvelli等[10]对三维编织复合材料疲劳性能进行了分析,发现三维编织复合材料在所有纺织复合材料中具有最好的拉伸疲劳性能。徐焜、李典森和曹海建等[11-13]通过试验对三维编织复合材料拉伸和压缩性能进行了研究。郑锡涛等[14]对三维编织复合材料冲击后压缩性能进行了研究。关志东等[15-16]采用渐进失效对含开孔层合板在拉伸和压缩载荷下的失效进行了分析,发现其模型可以很好地预测含开孔层合板的损伤起始、扩展和失效强度。Xu等[17]尝试采用断裂力学方法对含开孔层合板强度进行预测。综上研究发现,关于三维编织复合材料的研究多针对材料性能试验研究或者单胞均质化研究,而关于三维编织复合材料含缺陷时的力学分析则鲜有报导。传统层合复合材料对于缺陷非常敏感,优异的损伤容限性能是三维编织复合材料得以应用的最重要的原因。因此开展缺陷对三维编织复合材料力学性能的影响研究,对三维编织复合材料工程应用具有重要参考价值。本文首先对拉伸载荷下开孔三维编织复合材料含强度进行试验研究,同时观察缺陷造成的应力再分布,并基于渐进损伤分析方法和传统含缺陷失效准则对开孔后三维编织复合材料缺陷强度进行了预测。
1 试验研究
2 试验设计
试验件采用HEXCEL AS4-6K碳纤维作为增强材料,WEST SYSTEM 105系列环氧树脂作为基体材料。预制件为基本编织结构(三维四向),在四步法(1×1)三维编织机加工完成预制件,预制件如图1所示。3D编织复合材料的制备采用RTM工艺(树脂传递成型)。
根据美国标准协会复合材料压缩性能测试标准ASTM D3039[18]和复合材料含开孔压缩性能测试标准ASTM D5766[19]制备标准试验件,无缺陷和含缺陷试验件的尺寸分别如图2a)和2b)所示,实际试件如图2c)和2d)所示。对于无缺陷试件,在加持端由于应力集中容易造成试件断裂,应在试件两端贴保护片,如图2b)所示。含缺陷试件拉伸时未贴保护片。缺陷为机械加工圆孔,如图2c)所示,试件孔直径为5 mm。
不含缺陷和含缺陷三维编织复合材料试验件的准静态拉伸试验步骤分别参照ASTM D3039和D5766进行。每组样品应取5个有效数据试验以获得其平均强度和弹性模量。试验机为INSTRON测试系统,试验过程中拉伸速率为2 mm/min。
 |
图1 三维编织复合材料预制件 |
 |
图2 试件尺寸和几何形状 |
3 试验结果
试件拉伸性能如表 1所示。可以看出, 无开孔时试件强度为1 279 MPa, 失效应变为1.76%;引入开孔缺陷后, 试件强度降低为951 MPa, 断裂应变为1.3%。引入缺陷后3D编织复合材料仍然可以保留高达84%的剩余拉伸强度, 但引入开孔后会加速试件失效。含开孔试件拉伸断裂形态和断裂截面如图3所示, 含开孔3D编织复合材料在拉伸载荷下失效模式主要为沿孔横向断裂。
3D编织复合材料拉伸性能
 |
图3 试件断裂形态 |
4 开孔三维编织复合材料强度预测模型
5 传统开孔强度准则判准
在层合板开孔板拉伸强度预测研究方面, 研究方法主要有孔边应力法和逐渐损伤分析方法。而Whitney等[20-21]提出的点应力失效准则(PSC)和平均应力失效准则(ASC), 由于便于实施, 虽然预测的强度一般小于实际的承载能力, 但是在层合板强度预测中应用广泛。此处采用这2种准则对开孔三维编织复合材料板剩余强度进行预测, 下面对这2种准则进行介绍。
应力分布从B点开始至无穷远处应力逐渐递减, 其分布服从(1)式[22]
此处
KT∞为孔边缘应力集中系数; Aij(i, j=1, 2, 6)为面内刚度系数, 1方向为平行于载荷方向, 2方向为垂直与载荷方向。同时KT∞可用工程常数来表示[23]
式中:σ∞为沿X轴无穷远处应力, 即为载荷P; E11, E22, v12, G12为三维编织复合材料性能参数, E11为最大弹性模量方向, 本例为拉伸载荷方向。
点应力失效准则(PSC):
Nuismer和Whitney [20-21]通过(1)式获得点应力准则, PSC假定试件应力σy距离开孔一定长度d0时等于试件无缺陷强度, 即为
因为应力集中系数在点(d0, 0)针对不同孔尺寸是不同的, 因此该方法可以用来预测不同尺寸对缺陷强度的影响。则推导出含开孔缺陷时试件强度为
式中
平均应力准则(ASC):
该应力准则考虑力在一定特征长度内的平均应力等于试件强度时则含缺陷试件失效, 即在距离开孔边界一定长度a0内的平均σy等于或者大于无缺陷板的强度
则含开孔缺陷时试件强度为
式中:
σN, σ0分别为试件含缺陷强度和不含缺陷强度;d0, a0为经验特征长度。
6 渐进失效开孔板强度预测
传统开孔板失效准则实施简单, 但该方法不能模拟构件失效过程。渐进失效分析方法在复合材料失效分析中被广泛采用, 其具体思路为采用一定的损伤失效判定准则和材料性能的刚度折减方法来模拟试件在外界载荷下的损伤起始、扩展和最终破坏模式。
7 失效准则
本文采用了Hashin、Tsai-Wu、Puck、Chang-Chang、LaRC02等不同失效准则, 并对不同准则预测强度进行对比。鉴于Hashin、Tsai-Wu、Puck等失效准则已在相关论文中进行了大量介绍, 此处不再冗赘。而损伤演化则采用损伤变量累积的方法, 此处也不再详细介绍。本文主要详细介绍LaRC02失效准则[24]。
LaRCO2准则标识单向复合材料中的纤维失效和基体开裂。纤维失效进一步分为3个可能的失效模式:纤维拉伸失效、基体压缩下的纤维失效、基体拉伸下的纤维压缩失效。基体开裂也可分为3个可能的失效模式:拉伸形式的基体开裂、压缩形式的基体开裂、适度双轴压缩下的基体开裂。如果失效指数(FI)等于或超过1.0, 则发生失效(纤维失效或基体失效)。
纤维拉伸失效:
如果纵向法应力(σ11)为正,拉伸纤维失效准则为
ε11是当前纵向应变, ε1T是纤维拉伸失效下的纵向应变。
基体压缩下的纤维压缩失效有2种可能:
如果横向法向应力(σ22m)为正, 则
如果横向法向应力(σ22m)为负, 则
此处
拉伸基体失效
如果横向法向应力(σ22)为正, 拉伸基体失效准则为
XT=σ11为在纵向拉伸失效下的值,XC=σ11为在纵向压缩失效下的值,YT=σ22为在横向拉伸失效下的值,SL=σ12为在纵向剪切失效下的绝对值。α0为单轴压缩下破裂面的角度(设置为53°),ϕ为失效断裂面的角度。
8 开孔板材料性能常数
在进行有限元分析时需要3D编织复合材料各个方向的材料性能常数。通过试验可以测得三维编织复合材料的纵向弹性模量和纵向拉伸强度, 但很难获得材料的所有力学性能参数。此处采用Ko等[5]提出的FGM模型来对三维编织材料性能参数进行预测。
试验所得结果与FGM所预测的三维编织复合材料的材料性能和强度如表 2所示。可以发现所预测1方向的强度和模量与试验结果非常接近, 其余方向所预测材料力学性能参数将用于渐进失效有限元模型中。
3D编织复合材料强度和性能常数
9 开孔板有限元模型
开孔板模型及其网格离散如图5所示。
本文中有限元分析基于商用软件Abaqus/Standard平台, 通过用户子程序UMAT来定义材料属性、损伤准则和刚度折减方法。复合材料单元采用C3D8R实体单元, 单元数目为13 656。模型尺寸为25 mm×250 mm×3 mm。由于三维编织无层间概念, 同时三维编织复合材料本身为一体化结构, 因此采用宏观尺度进行建模。同时需要注意的是, 本例施加载荷方向为最大材料性能方向。
10 开孔三维编织复合材料强度预测结果
11 孔周边应力分析
由图4和Lekhnitskii理论知, 正交各向同性材料圆孔周边最大应力点位于沿X轴方向与孔交界处B点, 应力集中系数Kπ/2=5.45倍最大载荷; 最小应力处位移沿X轴与孔交界处, 为-0.71倍外加载荷, 受压应力载荷。由此可以预判在拉伸载荷下, 失效会起始于B点。基于Abaqus对沿孔周边应力进行分析。施加40 MPa载荷时, 孔周边应力如图6所示。发现此时最大应力值为275 MPa, 为拉应力; 最小应力值为-1.4 MPa, 压应力。而根据Lekhnitskii理论, 最小应力应为-28 MPa, 最大应力应为205 MPa。可以发现结果有一定误差, 但全局应力分布体势较为吻合。后期需要相关试验予以验证, 如DIC等检测方法。
三维编织复合材料沿孔边界垂直于载荷方向应力分布如图7所示。应力最大值靠近孔边界处, 之后沿X轴方向迅速下降, 在距离孔边界6 mm之后应力集中基本消失, 应力值接近施加载荷值。可知, Lekhnitskii理论分析模型与Abaqus模型所得起始端应力集中系数较为一致。
 |
图4 孔周边应力分析 |
 |
图5 有限元模型网格图 |
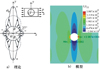 |
图6 孔周边应力 |
 |
图7 三维编织复合材料应力分布 |
12 预测强度结果对比
图8为3D编织复合材料试验和有限元模型的应力应变曲线。可以看出, 有限元模型强度值低于试验结果。主要原因为有限元模型中的计算所得应力集中系数高于试验观察和Lekhnitskii理论, 会造成试件过早失效, 因此有限元方法预测元度值会低于实际值。
关于含开孔三维编织复合材料强度预测方面, 基于PSC和ASC准则时, 特征长度d0, a0分别取1.38 mm[25]和3.75 mm[21]; 渐进失效分析中材料性能常数基于试验和FGM预测结果, 见表 2。基于不同失效准则的渐进失效预测强度、PSC和ASC预测强度与试验结果对比如表 3所示。可以看出所有预测结果均低于试验值, 但误差均在20%以内。基于PSC准则所预测结果最为接近试验值, 误差仅为5%。有限元分析中, 基于LaRCO2强度准则所得结果误差最小, 为10%。
3D编织复合材料试验和理论预测强度对比 MPa
基于Tsai-Wu失效准则的三维最终失效形态如图9所示。在Tsai-Wu失效准则下的开孔试件试件形式为严格横向断裂。基于不同失效准则的失效形态如图10所示, 可以发现失效形态均较为接近。缺陷均起始于孔周边并沿孔横向演化最终导致试件断裂。基于LaRCO2强度准则的三维编织复合材料损伤演化如图11所示。损伤首先为树脂断裂造成, 起始于孔周边与载荷方向垂直交界处, 然后沿孔横向扩展, 最后导致纤维拉伸断裂并导致试件突然断裂失效。该失效准则下试件仿真断裂形态最接近试验结果。
 |
图8 三维编织复合材料应力-应变曲线 |
 |
图9 基于Tsai-Wu失效准则失效形态 |
 |
图10 基于不同失效准则的3D编织复合材料失效形态 |
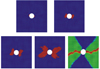 |
图11 3D编织复合材料损伤演化云图 |
13 结论
1) 本例中三维编织复合材料引入开孔后时够保留84%的保剩余拉伸强度。
2) 基于Abaqus的孔周边和沿孔垂直于载荷方向应力分布与Lekhnitskii理论预测较为吻合, 应力集中点位于垂直于载荷方向与孔交界处。
3) 含开孔三维编织复合材料在拉伸载荷下失效模式为裂纹沿应力集中点萌生并横向扩展, 最终导致结构件失效, 与有限元分析失效形式一致。
4) PSC准则相对ASC准则可以更为准确地预测三维编织复合材料含缺陷时的拉伸强度。渐进失效分析时, 基于LaRC02失效准则可以较为准确地预测含开孔时3D编织复合材料的拉伸强度及损伤演化过程。
References
- CAMPONESCHI E T, WALL L, CRANE R M. Theoretical and Experimental Analysis of Multidirectionally-Braided Composites[R]. AB-A172694, 1986 [Google Scholar]
- MACANDER A B, CRANE R M, CAMPONESCHI E T. Fabrication and Mechanical Properties of Multidimensionally(XD) Braided Composite Materials[C]//Seventh Conference on Composite Materials: Testing and Design, 1986 [Google Scholar]
- GAUSE L W, ALPER J M. Structural Properties of Braided Graphite/Epoxy Composites[J]. Journal of Composites, Technology and Research, 1987, 9 (4): 141– 150 [Article] [CrossRef] [Google Scholar]
- KO F K. Tensile Strength and Modulus of a Three-Dimensional Braid Composite[C]//Seventh Conference on Composite Materials: Testing and Design, 1986 [Google Scholar]
- KO F K. Three-Dimensional Fabrics for Composites[M]. Philadelphia, Elsevier Science Publishers, 1989: 129–171 [Google Scholar]
- XU K, XU X. Finite Element Analysis of Mechanical Properties of 3D Five-Directional Braided Compositesxy1 Materials Science and Engineering:A, 2008, 487 (1/2): 499– 509 [Article] [CrossRef] [Google Scholar]
- FANG G, JUN L, WANG B L, Progressive Damage and Nonlinear Analysis of 3D Four-Directional Braided Composites under Unidirectional Tension[J]. Composite Structures, 2009, 89(1): 126–133 [CrossRef] [Google Scholar]
- ZHANG C CURIEL-SOSA J, BUI T Q. A Novel Interface Constitutive Model for Prediction of Stiffness and Strength in 3D Braided Composites[J]. Composite Structures, 2017, 163: 32– 43 [Article] [CrossRef] [Google Scholar]
- SUN X, SUN C. Mechanical Properties of Three-Dimensional Braided Composites[J]. Composite Structures, 2004, 65 (3/4): 485– 492 [CrossRef] [Google Scholar]
- CARVELLI V, PAZMINO J, LOMOV S V, et al. Quasi-Static and Fatigue Tensile Behavior of a 3D Rotary Braided Carbon/Epoxy Composite[J]. Journal of Composite Materials, 2012, 47 (25): 3195– 3209 [Article] [CrossRef] [Google Scholar]
- XUN Kun, XU Xiwu, WANG Hai. Experimental Investigation of the Mechanical Properties of 3D 6-Directional Braided Composites[J]. Acta Materiae Compositae Sinica, 2005, 22 (6): 144– 149 [Article] (in Chinese) [Google Scholar]
- LI Diansen, LIU Zixian, LU Zixing, et al. Compressive Properties and Failure Mechanism of Three Dimensional and Five Directional Carbon Fiber/Phenolic Braided Composites[J]. Acta Materiae Compositae Sinica, 2008, 25 (1): 133– 139 [Article] (in Chinese) [Google Scholar]
- CAO Haijian, QIAN Kun, XU Wenxin, et al. Compressive Properties of Three-Dimensional Full Five-Directional Braided Composites[J]. Journal of Textile Research, 2013, 34 (8): 68– 70 [Article] (in Chinese) [Google Scholar]
- ZHANG Di, ZHENG Xitao, YANG Chao. Damage Tolerance Property Tests of 3D Braided Composites[J]. Acta Materiae Compositae Sinica, 2016, 33 (5): 1048– 1054 [Article] (in Chinese) [Google Scholar]
- GUAN Zhidong, LI Zengshan, LIU Debo, et al. Damage Analysis of Open-Hole Compression Laminates[J]. Acta Materiae Composite Sinica, 2012, 3: 167– 172 [Article] (in Chinese) [Google Scholar]
- LI Zengshan, GUAN Zhidong, HE Wei, et al. Damage Analysis of Open-Hole Tension Laminates[J]. Acta Materiae Composite Sinica, 2012, 29 (1): 169– 175 [Article] (in Chinese) [Google Scholar]
- XU X, TAKEDA S I, AOKI Y, et al. Predicting Notched Tensile Strength of Full-Scale Composite Structures from Small Coupons Using Fracture Mechanics[J]. Composite Structures, 2017, 180: 386– 394 [Article] [CrossRef] [Google Scholar]
- ASTM. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials[S]. D. 3039/D3039M-11, 1995 [Google Scholar]
- ASTM. Standard Test Method for Open Hole Tensile Strength of Polymer Matrix Composite Laminates[S]. D5766/D 5766M-11, 2011 [Google Scholar]
- WHITNEY J M, NUISMER R. Stress Fracture Criteria for Laminated Composites Containing Stress Concentrations[J]. Journal of Composite Materials, 1974, 8 (3): 253– 265 [Article] [CrossRef] [Google Scholar]
- NUISMER R, WHITNEY J M. Uniaxial Failure of Composite Laminates Containing Stress Concentrations Fracture Mechanics of Composites[M]. USA, ASTM Special Technical Rublication, 1975: 117–138 [Google Scholar]
- LEKHNITSKⅡ S G. Anisotropic Plates[M]. New York, Gordon and Breach, 1968 [Google Scholar]
- TAN S C. Stress Concentrations in Laminated Composites[M]. Ohio, CRC Press, 1994 [Google Scholar]
- DAVILA C, NAVIN J, SANJIB G. Failure Criteria for FRP Laminates in Plane Stress[C]//44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2003 [Google Scholar]
- KIM J K, KIM D S, TAKEDA N. Notched Strength and Fracture Criterion in Fabric Composite Plates Containing a Circular Hole[J]. Journal of Composite Materials, 1995, 29 (7): 982– 998 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 三维编织复合材料预制件 |
| In the text | |
 |
图2 试件尺寸和几何形状 |
| In the text | |
 |
图3 试件断裂形态 |
| In the text | |
 |
图4 孔周边应力分析 |
| In the text | |
 |
图5 有限元模型网格图 |
| In the text | |
 |
图6 孔周边应力 |
| In the text | |
 |
图7 三维编织复合材料应力分布 |
| In the text | |
 |
图8 三维编织复合材料应力-应变曲线 |
| In the text | |
 |
图9 基于Tsai-Wu失效准则失效形态 |
| In the text | |
 |
图10 基于不同失效准则的3D编织复合材料失效形态 |
| In the text | |
 |
图11 3D编织复合材料损伤演化云图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


