Path Planning Algorithm of Dijkstra-Based Intelligent Aircraft under Multiple Constraints

Ningyi Cheng; Zhiqian Liu; Yuqi Li

doi:10.1051/jnwpu/20203861284

All issues

Volume 38 / No 6 (December 2020)

JNWPU, 38 6 (2020) 1284-1290

Full HTML

Open Access

Issue		JNWPU Volume 38, Number 6, December 2020


Page(s)		1284 - 1290
DOI		https://doi.org/10.1051/jnwpu/20203861284
Published online		02 February 2021

JNWPU 2020, 38(6): 1284–1290

Path Planning Algorithm of Dijkstra-Based Intelligent Aircraft under Multiple Constraints

一种基于Dijkstra的多约束条件下智能飞行器航迹规划算法

Ningyi Cheng (程凝怡)¹, Zhiqian Liu (刘志乾)² and Yuqi Li (李昱奇)¹

¹ College of Safety and Ocean Engineering, China University of Petroleum-Beijing, Beijing 102249, China
² College of Mechanical and Transportation Engineering, China University of Petroleum-Beijing, Beijing 102249, China

Received: 16 January 2020

Abstract

Aiming at the rapid planning of the optimal flight path of the intelligent aircraft, considering the error constraints and correction probability constraints, a model for intelligent aircraft path planning under multiple constraints is constructed, and a global search algorithm based on Dijkstra algorithm is proposed to solve the model. By calculating the residual error and restricts flight distance, the basic Dijkstra algorithm is improved to make it more adaptable to solve the path planning under multiple constraints. At the same time, simulation experiment is conducted with the optimal goal of the shortest track length and satisfying the error constraints. The experimental results show that the aircraft passed a total of 18 correction points when it reached the destination. The total track length was 144 287.932 m, the vertical position error was 17.254 units, and the horizontal position error was 6.420 units. The results meet the error requirements. The results show that the intelligent aircraft path planning model and Dijkstra-based global search algorithm with multiple constraints are reasonable in solving such problems.

摘要

针对智能飞行器最优航迹快速规划问题，考虑误差约束及校正概率约束，构建多约束条件下智能飞行器航迹规划模型，并提出基于Dijkstra的全局搜索算法求解模型。所提算法通过计算剩余误差和约束飞行距离，对基础Dijkstra算法进行改进，使其在求解多约束条件下航迹规划问题时具有更好的适应性。同时，以航迹长度最短且满足误差约束为目标开展仿真实验，仿真实验结果为飞行器到达终点时共经过18个校正点，航迹长度144 287.932 m，垂直误差为17.254个单位，水平误差为6.420个单位，结果均满足误差要求，表明多约束条件下智能飞行器航迹规划模型和基于Dijkstra的全局搜索算法在解决此类问题方面具有一定的合理性。

Key words: Dijkstra algorithm / error correction / track planning / error constraint / correction probability constrain

关键字 : Dijkstra算法 / 误差校正 / 航迹规划 / 误差约束 / 校正概率约束

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

智能飞行器是在无人机技术基础上发展的一种高科技飞行设备, 最先用于军事侦查[1], 由于其体积小、质量轻、机动性强, 逐渐被广泛应用于人员搜救、航拍、物资输送等方面[2]。航迹规划技术是实现飞行器自主飞行并完成各种复杂飞行任务的关键[3], 其具体定义为在特定的飞行环境下, 在起点和目标点之间规划出基于约束条件的所有可能飞行路径, 它是一个包含多优化目标和多约束条件的非线性规划问题[4]。

一方面, 随着智能飞行器的日渐发展, 多约束条件下无人机航迹快速规划算法已经成为飞行器快速规划航迹的核心研究内容, 诸多学者在这方面做了大量研究。其中解决航迹快速规划问题的常用算法有[5]:Dijkstra算法、人工势场法、模拟退火算法、A^*算法、遗传算法、蚁群优化算法和粒子群优化算法。2008年沈延航和周洲[6]结合非线性规划方法、启发式搜索算法和最大值处理原理分别对攻击型无人机爬升、巡航、待机搜索阶段进行优化处理, 得到性能效益好、作战效益高的飞行航迹。2009年严江江等[7]针对三维航迹规划的实时性问题, 提出一种基于可行性优先的三维航迹规划方法。2012年李素娟[8]引入无人机飞行任务与战术目标约束, 建立系统的航路规划约束模型, 同时改进A^*算法求解模型, 得到有效的三维规划航迹。2014年辛培源[9]将无人机航迹规划中的约束分为性能约束和威胁约束分别进行研究, 并改进A^*算法得到最优航迹。2016年林鹏宏[10]融合RRT算法、模型预测及滚动优化等方法, 设计满足各种约束条件的飞行航迹规划策略。同年寇家勋[3]综合考虑静态和动态不确定性因素, 提出基于CC-RRT航迹规划方法与RR-GP轨迹估计算法的无人机在线航迹规划算法。2017年陶骥华[11]提出改进后的遗传算法、基于交互式多模型算法和模型预测控制算法的融合算法以及改进蚁群算法求解静态、动态、三维空间环境下的最优航迹。2018年Zhao等[12]研究了计算智能方法在求解无人机航迹规划时较数学和传统建模方法的优越性。2019年Wu[13]基于粒子群算法提出分阶段任务规划, 降低多约束条件算法求解难度。同年Shao等[14]提出了综合改进的粒子算法，提高了求解最优路径的快速性和最优性。

另一方面, 精确的导航定位技术是智能飞行器成功完成飞行任务的重要保证, 由于系统结构限制, 飞行器的定位系统存在一定误差, 当误差积累到一定程度将导致任务失败。所以, 许多学者针对多类型飞行器特征进行研究, 针对性地提出了新的导航系统以及误差补偿算法和误差修正技术, 使飞行器能精准地完成飞行任务[15-19]。为消除无人机定位的不规则误差, Wu等[20]引入RTS平滑算法进一步修正粒子群算法的无人机航迹规划最优解。

综上所述, 学者们的研究集中在考虑飞行环境和机动性能约束下的无人机航迹规划算法和导航技术的改进两方面, 但综合考虑误差修正和航迹规划的研究较少。基于此, 本文将结合飞行器飞行过程中定位误差的累积和修正约束, 对三维空间下静态环境中智能飞行器最优航迹规划问题进行研究。

1 智能飞行器多约束航迹规划模型

智能飞行器为执行任务需从A点飞往B点, 飞行区域三维空间如图 1所示。飞行器飞行过程中会出现定位误差, 影响任务执行, 为此, 依据地形设定误差校正点, 圆形为水平误差校正点, 方形为垂直误差校正点。

图1

飞行器航迹规划区域示意图

飞行器初始状态下误差为0, 飞行过程中会产生随距离呈线性增长的垂直误差和水平误差, 但经过误差校正后要求到达终点时垂直误差和水平误差均在限定值θ内, 即满足(1)式约束。

式中:n表示飞行器经过校正点的数量; i表示飞行器从起点出发经过的第i个校正点(1≤i≤n); L表示飞行器航迹长度; 下标v表示垂直方向; 下标h表示水平方向; d_i表示第i-1个误差校正点与第i个误差校正点之间的距离; e_i表示飞行器在第i-1个误差校正点与第i个误差校正点之间所产生的误差; E_{i, r}和E_{i, h}分别表示飞行器在误差校正点P_i处的垂直和水平误差。

此外, 垂直误差校正点在垂直误差不大于α₁个单位, 水平误差不大于α₂个单位时可将垂直误差校正为零, 水平误差保持不变; 水平误差校正点在垂直误差不大于β₁个单位, 水平误差不大于β₂个单位时可将水平误差校正为零, 垂直误差保持不变。但由于飞行环境具有不确定性, 使得部分校正点成功将误差校正为零的概率为P, 且垂直误差校正点校正失败后的垂直误差为min(u, 5)个单位(u为校正前误差), 水平误差不变; 水平误差校正点校正失败后的水平误差为min(u, 5)个单位, 垂直误差保持不变。基于此, 将上述约束分为以下4种情况讨论，其中j表示校正点类型判断, j=1代表垂直校正, j=0代表水平校正; f_i表示问题校正点判断, f_i=1代表问题校正点, f_i=0代表正常校正点; r_k代表问题校正点成功校正的概率。

情况1 若满足E_{k-1, v}+e_{k, v}≤α₁, E_{k-1, h}+e_{k, h}≤α₂, j=1, f_i=1, r_k < P则

情况2 若满足E_{k-1, v}+e_{k, v}≤α₁, E_{k-1, h}+e_{k, h}≤α₂, j=1, f_i=0或满足E_{k-1, v}+e_{k, v}≤α₁, E_{k-1, h}+e_{k, h}≤α₂, j=1, f_i=1, r_k≥P则

情况3 若满足E_{k-1, v}+e_{k, v}≤β₁, E_{k-1, h}+e_{k, h}≤β₂, j=0, f_i=1, r_k < P则

情况4 若满足E_{k-1, v}+e_{k, v}≤β₁, E_{k-1, h}+e_{k, h}≤β₂, j=0, f_i=0或满足E_{k-1, v}+e_{k, v}≤β₁, E_{k-1, h}+e_{k, h}≤β₂, j=0, f_i=1, r_k≥P则

建立飞行器多约束条件下的航迹规划模型关键在于确定途径校正点的位置坐标及顺序, 由飞行器出发地、目的地以及所有校正点位置坐标信息, 并根据航迹长度尽可能小的优化目标可建立如下目标函数。

2 基于Dijkstra的全局搜寻算法

根据误差随距离的积累规律, 将误差约束转化为距离约束。结合点集与权值思想, 并对比O-D距离矩阵, 通过循环迭代得到距离约束矩阵, 最终以距离约束矩阵为基础, 设计基于Dijkstra的全局搜寻算法。

2.1 剩余误差计算

考虑误差校正点的约束条件, 以执行变量P_{i, f_b, g_b, j}作为校正点的功能判断依据, 如表 1所示, 以0-1变量f_b, g_b, j作为校正点的类型判断依据, 其中, b表示校正点编号。

表1

校正点类型判断

若同时满足(f_b=1)&&(g_b=1)&&(r_k < P), 则P_{i, 1, 1, j}点处误差校正失败, 其对应的剩余垂直误差和水平误差可表示为

否则P_{i, 1, 1, j}点处误差校正成功, 其对应的剩余垂直误差和水平误差可表示为

2.2 飞行距离约束

因误差与飞行距离呈线性关系, 故由第i个点飞往第i+1个点应满足相应距离约束C_i。其计算方式如(9)式所示。

2.3 算法求解步骤

根据航迹点坐标信息, 可得到各点之间的O-D距离矩阵, 以变量w_ij表示航迹点p_i和p_j之间的直线距离, 同时引入点集V={p₁, p₂, p₃, …, p_m}表示航迹点集合, 其中航迹点的个数|V|=m。以Q={q_s}表示遍历点集合, 以权值集合D=[d(p₁), d(p₂), d(p₃), …, d(p_m)]表示从起点A到各个点的当前迭代过程中的最短路径。设误差校正矩阵具体算法步骤如下:

Step1 变量初始化

令d(p₁)=0;初始化距离约束矩阵Y, 令y_ij=w_ij。当满足w_1j≤C₁时, 令p_j∈Q, 更新集合Q;

Step2 修正距离约束矩阵

以集合Q中首个元素p_k为基准, 以距离约束C_k为参照量, 修正距离约束矩阵:若y_kj>C_k, 则y_kj=∞, 否则保持不变;

Step3 修正最短路径权值

选择集合Q中首个元素p_k, 提取其对应权值d(p_k), 修正最短路径权值:d(p_j)=min{d(p_j), d(p_k)+y_kj};

Step4 更新遍历点集

从集合Q中剔除Step2中已选用的元素, 其余元素依序保留。若Step2中最短路径权值d(p_j)发生变化, 则将元素p_j依序补充至集合Q中;

Step5 更新距离约束矩阵

单次迭代结束, 还原距离约束矩阵Y, 令y_ij=w_ij;

Step6 循环迭代

重复执行Step2~5, 若集合Q=∅, 则终止算法;

Step7 最短路径回溯

算法循环执行结束, d(p_j)的终值即为从起点p₁到其余各校正点的最短路径长度, 运用回溯算法可得到最短路径。

详细的算法流程如图 2所示。

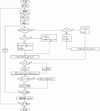图2

考虑问题校正点下对飞行器航迹寻优的算法流程

3 算例仿真

根据上述建立的航迹规划模型以及提出的全局搜寻算法, 设置相关参数(参数取值可进行相关调整), 如表 2所示; 同时由MATLAB随机函数生成起点、终点以及325个误差校正点坐标, 部分坐标值如表 3所示。

表2

模型参数值设置

表3

误差校正点坐标

利用MATLAB编程实现上述算法, 进行仿真实验, 仿真结果显示, 飞行器共经过校正点的数目为18, 所经过航迹长度为144 287.932 m。飞行器航迹三维视图如图 3所示, 图中圆形点为水平误差校正点, 正方形点为垂直误差校正点, 飞行器具体航迹如下:0→169→266→270→248→194→205→196→119→243→73→82→274→39→186→16→282→141→124→326。

图3

飞行器飞行轨迹三维图

飞行器从起点出发经过的误差校正点编号及校正前后误差如表 4所示。由表 4可知, 飞行器在校正点进行误差校正时, 校正前后误差皆满足约束条件中α₁, α₂, β₁和β₂的取值, 且飞行器到达终点B时, 垂直误差为17.254, 水平误差为6.420, 均在误差约束范围内, 表明飞行器可以正常完成飞行任务, 故该仿真结果具备一定合理性。

表4

误差校正点编号及校正前后误差

4 结论

针对智能飞行器航迹规划问题, 通过模型建立、算法设计以及实例仿真, 最终得出以下结论:

1) 以误差约束和基于随机概率的误差校正规律为研究重点, 建立多约束条件下智能飞行器航迹规划模型, 求解误差允许范围内最优航迹。

2) 基于Dijkstra设计“全局搜寻”算法对模型进行求解。利用遍历思想迭代求解最短路径, 回溯得到相应校正方案。

3) 利用MATLAB软件生成随机数据组进行实例仿真, 排除算法偶然性, 以此验证该算法的正确性与适用性, 最终实现航迹最短的优化目标。

本文未考虑飞行器水平转弯与垂直俯仰等问题, 鉴于此, 笔者将在之后对该问题进行深层次研究, 进而提高模型与算法的完善性和实用性。

References

Zhang Taoran. Structural Design of Intelligent Aircraft[J]. Henan Science and Technology, 2018 (26): 122– 123 (in Chinese) [Google Scholar]
Shang Hong, Li Yigang, Li Yanfeng, et al. Intelligent Aircraft and Disaster Rescue[J]. China Emergency Rescue, 2007 (2): 26 (in Chinese) [Google Scholar]
Kou Jiaxun. Research on Route Planning for Unmanned Aerial Vehicles under Uncertain Environment[D]. Beijing: Beijing Institute of Technology, 2016 (in Chinese) [Google Scholar]
Wang Qiong, Liu Meiwan, Ren Weijian, et al. Overview of Common Algorithms for UAV Path Planning[J]. Journal of Jilin University, 2019, 37 (1): 58– 67 (in Chinese) [Google Scholar]
Wang Lei. Research on Navigation Technology for UAV in Complex Geografic Conditions[D]. Harbin: Harbin Institute of Technology, 2013 (in Chinese) [Google Scholar]
Shen Yanhang, Zhou Zhou. A Method of Cooperative Engagement Control for Attack Uninhabited Air Vehicles[J]. Acta Armamentarii, 2008 (10): 1277– 1280 (in Chinese) [Google Scholar]
Yan Jiangjiang, Ding Mingyue, Zhou Chengping, et al. 3D Route Planning Based on Feasible First Search[J]. Journal of Astronautics, 2009, 30 (1): 139– 144 (in Chinese) [Google Scholar]
Li Sujuan. Research on UAV Route Planning and Evaluation Method[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese) [Google Scholar]
Xin Peiyuan. Research on Route Planning Method of UAV Based on Complex Constraints of 3D Environment[D]. Beijing: Capital Normal University, 2014 (in Chinese) [Google Scholar]
Lin Penghong. Research on Tracking Control and Trajectory Planning of Quadrotor with Multi Constraints[D]. Harbin: Harbin Institute of Technology, 2016 (in Chinese) [Google Scholar]
Tao Jihua. Research on Path Planning Algorithms for Unmanned Aerial Vehicle[D]. Hangzhou: Hangzhou Dianzi University, 2017 (in Chinese) [Google Scholar]
Zhao Yijing, Zheng Zheng, Yang Liu. Survey on Computational-Intelligence-Based UAV Path Planning[J]. Knowledge-Based Systems, 2018, 158: 54– 64 [CrossRef] [Google Scholar]
Wu Yu. Coordinated Path Planning for an Unmanned Aerial-Aquatic Vehicle(UAAV) and an Autonomous Underwater Vehicle(AUV) in an Underwater Target Strike Mission[J]. Ocean Engineering, 2019, 182: 162– 173 [CrossRef] [Google Scholar]
Shao Shikai, Yu Peng, He Chenglong, et al. Efficient Path Planning for UAV Formation via Comprehensively Improved Particle Swarm Optimization[J/OL]. (2019-08-18)[2020-01-06]. [Article] [Google Scholar]
Jia Xin, Yang Shuwen, Zhang Zhihua, et al. A Method to Improve Positioning Accuracy of UAV Image Based on POS Data[J]. Remote Sensing Information, 2019, 34 (4): 92– 96 (in Chinese) [Google Scholar]
Tang Jin. Research on High Precision Autonomous Navigation and Monitoring Technology of UAV Based on BDS[D]. Harbin: Harbin Engineering University, 2019 (in Chinese) [Google Scholar]
Ge Changli. Investigation on High Precision GPS Positioning Method and Its Application in UAV Positioning System[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2018 (in Chinese) [Google Scholar]
Zhang Yongming. Research on Error Elimination Technology of Remote Sensing and Positioning System for Light and Small UAV[J]. Computer Measurement & Control, 2018, 26 (5): 234– 236 (in Chinese) [Google Scholar]
Yang Zhe. The Error Compensation Technology of Aircraft Navigation System[D]. Beijing: Beijing Institute of Technology, 2016 (in Chinese) [Google Scholar]
Wu Xiande, Bai Wenbin, Xie Yaen, et al. A Hybrid Algorithm of Particle Swarm Optimization, Metropolis Criterion and RTS Smoother for Path Planning of UAVs[J]. Applied Soft Computing, 2018, 73: 735– 747 [CrossRef] [Google Scholar]

All Tables

校正点类型判断

模型参数值设置

误差校正点坐标

误差校正点编号及校正前后误差

All Figures

	图1 飞行器航迹规划区域示意图
In the text

	图2 考虑问题校正点下对飞行器航迹寻优的算法流程
In the text

	图3 飞行器飞行轨迹三维图
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Zhang Taoran. Structural Design of Intelligent Aircraft[J]. Henan Science and Technology, 2018 (26): 122– 123 (in Chinese) [Google Scholar]

[2] Shang Hong, Li Yigang, Li Yanfeng, et al. Intelligent Aircraft and Disaster Rescue[J]. China Emergency Rescue, 2007 (2): 26 (in Chinese) [Google Scholar]

[3] Kou Jiaxun. Research on Route Planning for Unmanned Aerial Vehicles under Uncertain Environment[D]. Beijing: Beijing Institute of Technology, 2016 (in Chinese) [Google Scholar]

[4] Wang Qiong, Liu Meiwan, Ren Weijian, et al. Overview of Common Algorithms for UAV Path Planning[J]. Journal of Jilin University, 2019, 37 (1): 58– 67 (in Chinese) [Google Scholar]

[5] Wang Lei. Research on Navigation Technology for UAV in Complex Geografic Conditions[D]. Harbin: Harbin Institute of Technology, 2013 (in Chinese) [Google Scholar]

[6] Shen Yanhang, Zhou Zhou. A Method of Cooperative Engagement Control for Attack Uninhabited Air Vehicles[J]. Acta Armamentarii, 2008 (10): 1277– 1280 (in Chinese) [Google Scholar]

[7] Yan Jiangjiang, Ding Mingyue, Zhou Chengping, et al. 3D Route Planning Based on Feasible First Search[J]. Journal of Astronautics, 2009, 30 (1): 139– 144 (in Chinese) [Google Scholar]

[8] Li Sujuan. Research on UAV Route Planning and Evaluation Method[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese) [Google Scholar]

[9] Xin Peiyuan. Research on Route Planning Method of UAV Based on Complex Constraints of 3D Environment[D]. Beijing: Capital Normal University, 2014 (in Chinese) [Google Scholar]

[10] Lin Penghong. Research on Tracking Control and Trajectory Planning of Quadrotor with Multi Constraints[D]. Harbin: Harbin Institute of Technology, 2016 (in Chinese) [Google Scholar]

[11] Tao Jihua. Research on Path Planning Algorithms for Unmanned Aerial Vehicle[D]. Hangzhou: Hangzhou Dianzi University, 2017 (in Chinese) [Google Scholar]

[12] Zhao Yijing, Zheng Zheng, Yang Liu. Survey on Computational-Intelligence-Based UAV Path Planning[J]. Knowledge-Based Systems, 2018, 158: 54– 64 [CrossRef] [Google Scholar]

[13] Wu Yu. Coordinated Path Planning for an Unmanned Aerial-Aquatic Vehicle(UAAV) and an Autonomous Underwater Vehicle(AUV) in an Underwater Target Strike Mission[J]. Ocean Engineering, 2019, 182: 162– 173 [CrossRef] [Google Scholar]

[14] Shao Shikai, Yu Peng, He Chenglong, et al. Efficient Path Planning for UAV Formation via Comprehensively Improved Particle Swarm Optimization[J/OL]. (2019-08-18)[2020-01-06]. [Article] [Google Scholar]

[15] Jia Xin, Yang Shuwen, Zhang Zhihua, et al. A Method to Improve Positioning Accuracy of UAV Image Based on POS Data[J]. Remote Sensing Information, 2019, 34 (4): 92– 96 (in Chinese) [Google Scholar]

[16] Tang Jin. Research on High Precision Autonomous Navigation and Monitoring Technology of UAV Based on BDS[D]. Harbin: Harbin Engineering University, 2019 (in Chinese) [Google Scholar]

[17] Ge Changli. Investigation on High Precision GPS Positioning Method and Its Application in UAV Positioning System[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2018 (in Chinese) [Google Scholar]

[18] Zhang Yongming. Research on Error Elimination Technology of Remote Sensing and Positioning System for Light and Small UAV[J]. Computer Measurement & Control, 2018, 26 (5): 234– 236 (in Chinese) [Google Scholar]

[19] Yang Zhe. The Error Compensation Technology of Aircraft Navigation System[D]. Beijing: Beijing Institute of Technology, 2016 (in Chinese) [Google Scholar]

[20] Wu Xiande, Bai Wenbin, Xie Yaen, et al. A Hybrid Algorithm of Particle Swarm Optimization, Metropolis Criterion and RTS Smoother for Path Planning of UAVs[J]. Applied Soft Computing, 2018, 73: 735– 747 [CrossRef] [Google Scholar]