| Issue |
JNWPU
Volume 42, Number 2, April 2024
|
|
|---|---|---|
| Page(s) | 344 - 352 | |
| DOI | https://doi.org/10.1051/jnwpu/20244220344 | |
| Published online | 30 May 2024 | |
Research on the generation method of missing data for soft measurement based on GAN
基于GAN的软测量缺失数据生成方法研究
College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China
Received:
15
March
2023
To solve the problem of low precision in soft sensor models caused by sensor data loss in industrial processes, a new method of sensor data generation based on generative adversarial nets (GAN) is proposed. Firstly, the missing area of sensor data is detected by the isolated forest algorithm. Secondly, conditional generative adversarial nets (CGAN) are training using the attributes of missing data. By adding random sequences to the input conditions of CGAN as additional information, the data is generated iteratively in CGAN. The wasserstein generative adversarial nets gradient penalty (WGAN-GP) cost function is used to improve the stability of network training. Finally, a sampler is introduced to fill the sampled data into the missing region and form a complete data set to improve the accuracy of the soft sensing model. In this paper, the temperature sensor data of a nickel flash furnace is used as the target variable for soft-sensing modelling, and the feasibility and effectiveness of the proposed method to improve the accuracy of the soft-sensing model are verified.
摘要
针对工业过程中传感器数据缺失造成软测量模型精度低的问题,提出一种基于生成对抗网络(generative adversarial nets, GAN)的传感器缺失数据生成方法。利用孤立森林算法检测出传感器数据的缺失区域;利用缺失数据属性特征训练条件生成对抗网络(conditional generative adversarial nets, CGAN),在CGAN的输入条件中添加随机序列作为附加信息迭代送入CGAN中生成数据,并借助WGAN-GP(wasserstein generative adversarial nets gradient penalty)成本函数提高网络训练的稳定性;针对缺失区域检测结果引入采样器,将采样的数据填补进缺失区域,形成完整数据集,以提高软测量模型精度。以镍闪速炉温度传感器数据为目标变量进行软测量建模,验证所提出的提高软测量模型精度方法的可行性与有效性。
Key words: data missing / isolated forest / GAN / soft sensor model
关键字 : 数据缺失 / 孤立森林 / 生成对抗网络 / 软测量模型
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
工业过程中传感器技术是检测系统运行状态进而保证产品质量和生产系统平稳运行的关键所在。然而,系统安装空间、技术和成本等因素的限制,使得部分硬传感器配置难度大且降低企业经济效益,因此基于工业过程的软测量技术对预测难以测量变量显得尤为重要[1]。
软测量建模主要分为基于模型和基于数据驱动2种方法,随着数据量逐渐增大,数据驱动软测量建模已成为主要方法[2-3]。无论哪种建模途径,目前相关研究大多将重心放在如何提高软测量模型性能上。过于关注模型结构和训练方式,导致大部分研究者忽略了数据质量对软测量模型的影响[4]。同时,在实际工业系统中,传感器测量数据的采集过程也会对数据质量造成影响,如传感器电路接触不良、采样率不同或控制系统突然停止运行等,都会导致数据存在不同程度缺失。而采集的数据带有缺失部分,不可避免地会对数据驱动软测量模型精度带来不利影响。由此可见,完整的传感器数据集、良好的传感器数据质量以及合理的数据预处理方法是提高软测量模型精度的重要保障[5-6]。
分析发现,数据缺失通常有3种表现形式:完全随机缺失、随机缺失以及非随机缺失。完全随机缺失指数据的缺失不依赖于任何不完全变量或完全变量;随机缺失指某类数据的缺失依赖于其他完全变量;而非随机缺失指数据的缺失依赖于不完全变量[7-8]。无论哪种情况下的数据缺失,都将致使大量有效信息丢失,对分析数据特征等产生不利影响。近年来,针对这一问题,很多研究者将关注点放在缺失数据处理上,目前缺失数据处理方法主要包括删除法和插补法[8]。文献[9]利用删除法剔除数据集中缺失项的冗余特征数据,并使用朴素贝叶斯分类器达到较好的分类效果。文献[10]利用插补法将某一类数据均值作为插补值进行填充,最终实现缺失值的插补处理进而形成完整数据集。删除法是将带有缺失项数据直接删除,从而得到完整的数据集,该方法会丢弃掉数据里的大量有效信息,影响时间序列数据的连续性以及有用信息的提取。可见,删除法并不利于提高软测量模型精度。而插补法通过改进机器学习模型的预测值填补缺失区域使其完整。有研究者将K最近邻(K-nearest neighbor, KNN)用于缺失值填充进而实现小数据集扩充,然而该方法仅适用于缺失单个数据情况下的插补,对于连续的缺失值构成的区域其使用同一值填充,不符合实际工业过程。Elreedy等[11]将合成少数过采样技术(synthetic minority over-sampling technique, SMOTE)用于生成额外样本,使用扩充样本代替缺失值,但是SMOTE算法无法克服分布边缘化的问题,若被采样数据处于边缘分布,扩充数据将越来越边缘化。Jiang等[12]利用随机森林预测微塑料上弧菌属的相对丰度,用于建立长期和动态的检测系统,但随机森林预测填充过程中,忽略了原始数据的密度分布,预测值不一定符合工业过程正常运转的要求。
进入大数据时代后,众多具有优越性能的深度学习模型被用于自然语言处理(natural language processing, NLP)和计算机视觉(computer vision, CV)等领域,常借助模型提取数据中隐含信息,预测目标变量未来状态。其中生成对抗网络已经用于图像生成、音频生成等[13]领域,并且已被验证具有优越的预测效果。Yao等[14]提出一种微调插补GAN(fine-tuned imputation GAN, FIGAN),将下游模型-软测量结合到生成对抗插补网络中,实现特定下游任务的闭环插补-预测任务,然而当软测量预测误差较大时,将错误信息反馈给生成器,则插补数据与真实数据偏差更大。文献[15]使用WGAN(wasserstein generative adversarial nets)生成虚拟数据,通过增加数据量提高软测量模型精度,但未考虑到训练数据集缺失对软测量模型精度的影响。目前,GAN已经广泛用于各个领域,但用于工业过程中的缺失数据生成研究还非常有限。
综上,本文提出了一种基于GAN的填补缺失数据进而提升软测量模型精度的数据生成方法。主要贡献是将研究重点放在识别缺失区域位置及大小,通过采用CGAN对抗框架生成符合原始数据概率分布和工业过程正常运转条件的数据, 以进行缺失区域填充,确保了填充数据与原始数据特征的相似性。此外,还将WGAN-GP的成本函数引入CGAN中,保证了生成过程的稳定性。
1 理论分析
为了提升工业过程中通过软测量算法构建的软传感器测量精度,本文通过提升用于软测量的辅助传感器数据的数据完备性,为软测量算法的实施奠定基础。首先借助孤立森林算法,检测传感器测量数据的缺失区域;其次利用CGAN算法生成缺失部分数据;最后,根据孤立森林算法检测结果,采样生成缺失部分数据并形成完整数据集。该方法流程如图 1所示。
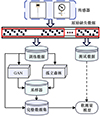 |
图1 基于GAN的传感器缺失数据生成方法框架图 |
2 基于孤立森林的数据缺失区域检测
为了提升工业过程软测量精度,需要确定的辅助传感器数据作为支撑,辅助传感器数据的完备性和软测量算法直接决定软传感器设计的可行性。因此,检测出其测量数据的缺失区域,为数据的有效生成及完备性的构建奠定基础。在异常点检测过程中,数据点的异常值越大,说明该点越特殊,而对于工业传感器数据,通过观察样本点的分布情况及其异常值,可反映出传感器的工作状况。因此,需要借助改进的异常点检测算法检测出缺失区域。首先使用异常点检测得出训练数据集中所有数据点的异常值,再根据由大到小排列的异常值,筛选出异常值最大的几个数据点,筛选出的数据点即为缺失区域两侧数据点,进而得出缺失区域位置及大小。
目前已有多种异常点检测算法,基于密度的异常点检测受近邻点参数设定影响较大且在大数据集上效率较低,而基于聚类的异常点检测主要功能为聚类,将不属于任何一簇的点视为异常点,故其检测效果不够理想。工业过程中需要及时分析、处理大量传感器数据,而孤立森林作为一种异常点检测算法[16],不需要计算点与点之间距离或密度分布,针对单个传感器数据能达成简单高效识别异常点的目的,且在单个传感器数据缺失的情况下,不必考虑到高维数据对检测算法的影响,故借助孤立森林检测工业传感器数据中的缺失区域效果更为理想。
孤立森林基于传感器缺失数据集X={x1, x2, x3, …, xn}, 其只包含单个特征q, 使用二叉树对该特征数据进行随机切分, 其中分割点为p, 直至将每个样本点被孤立于一个子空间中, 此时
式中: c(n)为给定n个子样本时的平均路径长度。建立孤立子树伪代码如算法1所示。
算法1 生成孤立子树Ftree(X, e, l)
输入: 带有缺失的传感器数据集X, 对于其中任一数据x∈X,|X|为X中的数据点个数,孤立子树高度l, 当前孤立子树高度e。
输出: 孤立子树Ftree
1) if e < l or |X|>1 then
从给定数据集X中随机选择介于最大值和最小值之间的分割点p
2) Xless←x≤p
3) Xgreater←x>p
4) return叶子节点N
{左节点Ftree(Xleft, e+1, l), 右节点Ftree(Xright, e+1, l), 分割值p}
5) else
6) return叶子节点N{x}
7) end if
计算异常分数如(2)式所示
式中: h(x)为样本x在每棵树上外部节点与根节点的距离;E(h(x))为h(x)在t棵树上的平均值。如果s≈1, 则为异常点; 如果s≪0.5, 则为正常点; 如果s≈0.5, 则为所有样本点无明显异常。
随后将数据集中每个数据点按照异常值由大到小排列, 筛选出M个异常值最大的数据点
式中: M为需要筛选的异常点个数;m为缺失区域个数。根据筛选出异常点个数M, 计算出缺失区域信息, 其伪代码如算法2所示。
算法2 生成孤立森林Fforest(X, t, ψ), 得出异常分数及缺失区域信息
输入: 有缺失的传感器数据集X, t棵孤立子树, 随机抽样样本数量ψ
输出: 孤立森林Fforest, X中n个样本异常分数s(x), X中的缺失区域信息
1) 初始化孤立森林Fforest(X, t, ψ)并设置树最高值ceiling(log2ψ)
2) for i=1 to t do
X′←在给定数据集X中随机抽样
3) Fforest=Fforest∪Ftree(X′, 0, l)
4) end for
5) return Fforest
6) for x∈X do
7) 根据(2)式计算s(x)
8) return s(x)
9) end for
10) 根据异常分数由大到小排序
11) 根据(3)式筛选M个异常数据点, 计算缺失区域信息
3 基于GAN的传感器缺失数据生成
3.1 数据生成算法原理
在检测出数据缺失区域的基础上, 以原始缺失数据作为GAN训练集生成数据, 通过算法设计, 实现缺失数据生成的目标。工业系统正常运行中, 传感器测量数据通常动态稳定在一定区间内。以镍闪速炉熔炼过程为例, 其炉壁温度传感器测量数据呈明显的高斯分布特性: 数据点在该区间内, 越接近中心区域, 分布密度最大; 越接近区间边缘, 即正常运转阈值, 则分布越稀疏。因此, 要求填补数据分布符合高斯分布且数据值在系统正常运转范围内。GAN作为一种生成模型, 可使生成器与判别器相互对抗优化, 最终使生成器将输入噪声分布近似拟合成原始数据的概率分布和数据值, 进而实现与原始数据各方面的相似性, 以此可将其用于生成新样本。
GAN由生成器与判别器两部分组成, 生成器将输入噪声分布拟合成传感器数据分布, 而判别器需要判断出某个样本点来自传感器数据集或生成样本。二者之间通过相互博弈, 使生成器达到近似传感器数据分布的要求[17]。GAN成本函数为
式中: 对数函数的底数取值为[1, +∞]间的任意值,x为传感器数据;Pdata(x)为传感器数据分布;z为生成器输入噪声;Pz(z)为噪声先验分布;G(z)为z经过生成器映射后的样本;D(x)为判别器判断x为训练数据的概率分布。
在优化GAN过程中, 生成器与判别器分别优化。假设先优化判别器网络, 使生成器网络参数不变, 此时对于任意给定的生成器, 其最优判别器DG*为
将DG*(x)结果代入(4)式中, 其成本函数可重新表达为
当且仅当Pg=Pdata时, (6)式值为-log4。因此最终的成本函数如(7)式所示
此时, 将GAN成本函数转化为使用div散度和JS散度衡量生成数据与传感器缺失数据分布的相似性。然而, 当2种分布未重合时, 其div散度趋近于无穷且JS散度恒定为log2,使用梯度下降算法优化参数时, 网络不能根据样本相似性度量结果更新参数, 进而导致模型训练不稳定及模式崩溃的问题。
流程工业中对传感器数据准确性及生成模型的稳定性有较高要求, 而GAN的模式易崩溃问题导致无法控制生成样本的模式, CGAN作为GAN的改进版本, 具有较好的稳定性, 故在此选用条件生成对抗网络。如图 2所示, 条件生成对抗网络可通过输入网络的附加信息, 使生成器按照指定的方向或类型生成虚拟样本。因此, 引入附加信息后极大地改善了训练稳定性, 且可改变附加信息进而生成理想的传感器数据样本[18]。可得CGAN成本函数为
此时生成器并不是学习GAN中传感器数据分布P(x), 而是在给定附加信息情况下的训练数据分布P(x|y)。
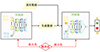 |
图2 CGAN数据生成结构图 |
3.2 GAN模式崩溃的改进方法
GAN和CGAN成本函数经过数学推导, 同样转化为div散度及JS散度, 求导后不能提供网络优化方向, 难以指导生成器或判别器每次优化程度。若某次生成器优化过度, 则判别器不能正确分辨生成数据来源, 生成器针对该漏洞生成相同的数据, 致使其不满足传感器数据动态稳定及高斯分布特点, 对填补缺失区域数据造成不利影响。若某次判别器优化过度, 则会导致全部生成数据被判断为假, 不能实现目标变量软测量建模。
为使生成模型能近似拟合传感器数据分布, 又引入WGAN-GP成本函数, 通过改进生成模型的成本函数使生成对抗网络训练更具鲁棒性, 其关键在于两点:
1) 使用Wasserstein distance度量2种样本相似性, 即使2种样本分布无重叠部分也能很好地线性表示二者距离, 给生成器与判别器网络提供优化方向。Wasserstein distance使用“最小转化距离”表示2种样本相似度,因此无论样本之间的差异多大, 都可以用梯度下降法更新网络参数, 达到稳定训练GAN的作用。此外, 还要求判别器参数每次更新梯度必须位于定义的K-Lipschitz函数阈值内, 即设置了梯度裁剪, 防止梯度更新过大, 致使网络权重值集中于裁剪阈值边缘, 限制网络学习能力。最终成本函数如(9)式所示
式中: f表示K-Lipschitz函数, 本文设f=1。
2) 在成本函数中额外添加梯度惩罚项: 在生成数据和原始数据之间做随机插值, 随后让此随机插值参与惩戒计算, 添加惩戒项后可以很好地使网络权重均匀分布, 对神经网络学习更加友好。可将惩戒项设为
因此, 通过应用改进的C-WGAN-GP(conditional Wasserstein generative adversarial nets gradient penalty)生成模型, 使得2种样本相似性度量结果不为某个恒定值, 进而防止网络梯度为零, 解决模式崩溃等问题, 稳定生成模型对抗过程, 使生成器与判别器最终稳定在纳什均衡状态, 保证了生成的缺失数据与原始传感器数据的密度分布与数据值保持较高相似性, 满足合理填补缺失区域的前提。
4 软测量模型构建
4.1 软测量模型构建方法
在获取辅助传感器完备数据的基础上, 进一步构建软测量算法模型, 实现软传感器设计。文中为说明缺失数据检测和生成对软测量结果的影响, 采用全连接神经网络(full connect neural network, FCNN)建立软测量模型。FCNN由输入层、隐藏层和输出层组成, 其中每层之间采用线性全连接方式, 通过调节层与层之间各节点之间的权值训练网络, 使其能够将输入辅助变量拟合成目标变量, 达到软测量目的。每个隐层输出为
式中: ωij为隐层传递下一层的权重;xi为上一层节点;aj为隐层偏置;g为激活函数。最终, 输出层的预测输出为
经过迭代优化参数, 最终可以将输入的辅助变量传感器数据拟合成目标变量传感器预测值, 实现对难以测量变量的软测量。
4.2 软测量模型评价指标
采用平均绝对误差(mean absolute error, MAE)和均方误差(mean square error, MSE)2种评价指标, 反映软测量模型预测值与真实值的偏差状况, 测试在不同缺失数据生成方法下的软测量模型精度。
平均绝对误差用于计算每个预测值与真实值之间的平均误差, 其计算公式为
均方误差可反映每个预测值与真实值之间误差的平方和的均值, 用于表示软测量模型预测误差状况, 进而可反映其预测精度, 其计算公式为
5 仿真实验研究
为了验证文中所提方法的有效性, 首先为检测传感器的缺失数据并生成完备数据集, 接着以此为基础建立软测量模型并进行精度测试, 验证数据生成对软测量算法的影响。
5.1 工艺流程及数据集介绍
本研究基于金川公司镍闪速炉熔炼工艺过程, 如图 3所示。在该工艺过程中, 首先原料经过球磨机制备熔剂和粉煤, 达到闪速炉冶炼所需的粒度; 其次, 对选矿产出的湿精矿进行干燥脱水处理, 为闪速炉熔炼过程提供达标的原材料; 接着将产出的干精矿与富氧空气由精矿喷嘴高速喷入闪速炉进行燃烧氧化反应, 收集高精度镍锍, 将精度不足的物料经过贫化电炉贫化, 尽可能提炼有价金属; 最后进行烟气脱硫处理。在氧化反应过程中, 当通入闪速炉体内的气体温度过高、压力过大或成分异常时, 通常要关闭风机及烟气通入阀门并打开烟气排出阀门, 使烟气直接排出, 防止烟气温度过高而损坏设备。因此, 闪速炉内温度是镍熔炼工艺的关键指标, 而炉内温度极高, 不适宜温度传感器的安装。根据工艺得出该变量受其他4个过程变量影响, 如表 1所示, 因此本研究通过过程变量传感器数据建立闪速炉内温度软测量模型。
对闪速炉系统传感器采集数据分析发现, 部分传感器带有明显的随机缺失区域, 并且缺失区域大小也为随机值。然而在实际工业系统运行中, 大部分时间处于正常运行状态, 仅偶发故障, 故采集到的镍闪速炉数据为系统正常运转时传感器数据。因此, 为模拟系统故障时传感器数据, 在采集得到5个传感器分别具有1 000条完整数据基础上,对x3进行人为处理得到缺失项, 如表 2所示。
 |
图3 镍闪速炉熔炼工艺流程图 |
过程变量表
缺失区域参数表
5.2 数据缺失区域检测
数据预处理后共有811条特征数据作为训练数据, 设置100个子树进行随机划分, 直至每个孤立区域内仅存在单个数据点, 计算每棵树上的平均最短路径并且得出每个数据点的异常分数。实现过程中, 原始数据集中缺失区域两侧一定范围内的数据点相较于其他数据点处于数据群的边缘地带, 其异常值较大, 故可被识别为异常点。越靠近缺失区域的数据点异常分数越大, 其中设定的3个缺失区域的边缘点, 共6个数据点的异常分数最大。因此, 使用孤立森林检测异常点并得出每个数据点的异常分数后, 将所有异常分数由大到小依次排列, 取前6个异常值最大的数据点的索引, 计算其两两之间间隔, 即为缺失区域位置及缺失范围。
通过实验证明使用孤立森林算法检测缺失区域, 其两侧数据点能被完好地识别为异常点。先前设置了3个缺失区域, 根据异常分数由大到小抽取出6个异常值最大的边缘点, 随后可以计算出每个缺失区域的位置及大小。通过观察检测结果, 与先前设置的完全一致。
5.3 缺失数据生成与填补
在生成数据部分, 采用CGAN作为对抗性框架。由于使用工业传感器数据训练生成模型, 基于此, 借助训练数据的均值、方差等7个数据属性作为附加的条件信息输入模型, 如表 3所示。为了使训练过程更加稳定, 在此对CGAN的成本函数稍加改进, 采用Wasserstein distance计算生成数据分布与训练数据分布的相似性, 并且引入了惩戒项增加其训练稳定性。在构建对抗模型中, 生成器采用卷积核长度为5、步长为3的CNN, 不断优化网络参数拟合训练数据分布。判别器采用4个隐藏层、每层3 000个节点的FCNN, 尽可能判断出输入数据来自生成数据分布还是训练数据分布。通过调节合适的参数, 得到生成器与判别器的成本函数曲线, 如图 4~5所示。可以看出, 改进的对抗框架训练稳定, 表明此时生成器与判别器处于纳什均衡状态, 生成器能稳定产生近似训练数据分布的数据。
训练过程中, 首先使用存在的811条数据训练生成模型使其稳定, 随后在附加信息中添加标准高斯分布噪声作为模型输入, 再次送入优化完成的模型中生成数据, 目的是使模型能更好地近似拟合出训练数据分布之外的缺失数据。图 6为使用GAN生成的数据与训练数据概率密度分布图, 其中红色曲线代表训练数据密度分布, 黑色曲线代表生成数据密度曲线。可以看出生成数据与原始数据的概率密度基本重合。
最后根据缺失区域位置及大小, 利用采样器从生成数据中, 根据其分布密度, 对不同密度数据采样出不同的数据量, 填补进原始缺失区域内, 形成完整训练集, 但每次采样数据量与每个缺失区域的大小相等。图 7为4种缺失值填补方法下的数据分布图, 可看出采用本文提出的缺失值填补方法生成的缺失数据密度分布符合原始数据分布特征, 而使用KNN、随机森林方法生成的数据分布过于密集, 不符合实际工业数据特征, 使用SMOTE方法生成的数据相对均匀, 不满足呈高斯分布的正常运转时数据分布条件。表 4为4种方法构成的完整数据与原始数据之间的div散度度量值, 相较于其他方法, 本文方法的填补数据与原始数据相似度最高, KNN方法的div散度值最大、相似度最低。因此使用本文提出的基于GAN的填补方法效果优越。
数据属性表
 |
图4 生成器损失曲线图 |
 |
图5 判别器损失曲线图 |
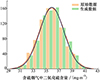 |
图6 原始数据与生成数据密度分布图 |
 |
图7 4种缺失数据填充效果图 |
4种填补的完整数据集与原始数据相似度
5.4 软测量预测模型建立及其测试
通过对原始缺失数据、本文提出的缺失值填补方法及KNN、随机森林、SMOTE共5种情况下的数据进行软测量建模, 并在200条测试数据下分别得出5种软测量模型预测值与MSE误差。如表 5所示, 从上述5种软测量模型在测试集上的预测误差对比可看出,具有缺失值的训练数据导致软测量模型精度最低, 而进行填补后的精度相对较高, 且本文填补方法的MSE误差最小, 填补数据最接近原始数据分布。图 8为有无缺失值填补处理的软测量模型MAE误差箱图, 无填补时模型误差最大, 而本文方法的预测中位数误差最小、预测置信区间也最小。可见完整的传感器数据集、良好的数据质量是建立高精度软测量模型的重要保障。
通过镍闪速炉熔炼工艺中的传感器数据, 对比有无缺失值处理及4种不同缺失值填补方法处理训练数据下的软测量模型预测误差, 可验证出本文提出的基于GAN的填补缺失数据、提高软测量模型精度的数据生成方法的有效性及优越性。
不同训练集下的软测量模型误差
 |
图8 软测量预测误差箱式图 |
6 结论
为了解决工业生产过程中传感器检测数据缺失造成软测量模型精度不高的问题,提出了一种填补缺失数据、提高软测量模型精度的数据生成方法。在该方法中,首先需要孤立森林算法检测出异常点,即能反映缺失区域在时间刻度上的位置及大小;其次利用C-WGAN-GP以缺失数据为输入,生成更多的数据;最后,再通过采样器采样出对应的数据量填补进原始数据集中,用于形成完整数据集且扩充数据量,另一方面也能够提高软测量模型精度。在实验中,通过验证C-WGAN-GP生成数据的准确性及软测量模型前后的误差精度,证明了该方法的优越性。
训练数据的质量及完整性是影响数据驱动模型精度的重要因素之一,故本文提出的缺失数据填补方法,同样适用于提高传感器故障诊断、故障分类等其他下游模型精度。在未来工作中,将改进GAN使其能够捕获特征数据的时间-空间相关性,使时序缺失数据更精准,下游软测量模型具有更高的预测精度。此外,针对GAN固有的模式崩溃等问题,将探索其他生成模型在缺失数据填补中的应用,如去噪扩散概率模型(denoising diffusion probability model, DDPM),以实现更稳定的填补任务。
References
- GOPAKUMAR V, TIWARI S, RAHMAN I. A deep learning based data driven soft sensor for bioprocesses[J]. Biochemical Engineering Journal, 2018, 136: 28–39. [Article] [CrossRef] [Google Scholar]
- KADLEC P, GABRYS B, STRANDT S. Data-driven soft sensors in the process industry[J]. Computers & Chemical Engineering, 2009, 33(4): 795–814 [CrossRef] [Google Scholar]
- SHANG C, YANG F, HUANG D, et al. Data-driven soft sensor development based on deep learning technique[J]. Journal of Process Control, 2014, 24(3): 223–233. [Article] [CrossRef] [Google Scholar]
- ZHU Q, HOU K, CHEN Z, et al. Novel virtual sample generation using conditional GAN for developing soft sensor with small data[J]. Engineering Applications of Artificial Intelligence, 2021, 106: 104497. [Article] [CrossRef] [Google Scholar]
- KHOSBAYAR A, VALLURU J, HUANG B. Multi-rate gaussian bayesian network soft sensor development with noisy input and missing data[J]. Journal of Process Control, 2021, 105: 48–61. [Article] [CrossRef] [Google Scholar]
- LYU Y, CHEN J, SONG Z. Synthesizing labeled data to enhance soft sensor performance in data-scarce regions[J]. Control Engineering Practice, 2021, 115: 104903. [Article] [CrossRef] [Google Scholar]
- ZHOU X, LIU X, LAN G, et al. Federated conditional generative adversarial nets imputation method for air quality missing data[J]. Knowledge-Based Systems, 2021, 228: 107261. [Article] [CrossRef] [Google Scholar]
- XIONG Zhongmin, GUO Huaiyu, WU Yuexin. Review of missing data processing methods[J]. Computer Engineering and Applications, 2019, 57(14): 27–38. [Article] (in Chinese) [Google Scholar]
- CHEN Jingnian. Research on selective bayesian classification algorithm[D]. Beijing: Beijing Jiaotong University, 2008 (in Chinese) [Google Scholar]
- WANG P, CHEN X. Three-way ensemble clustering for incomplete data[J]. IEEE Access, 2020, 8: 91855–91864. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- ELREEDY D, ATIYA A F. A comprehensive analysis of synthetic minority oversampling technique(SMOTE) for handling class imbalance[J]. Information Sciences, 2019, 505: 32–64 [Article] [CrossRef] [Google Scholar]
- JIANG J, ZHOU H, ZHANG T, et al. Machine learning to predict dynamic changes of pathogenic vibrio spp.abundance on microplastics in marine environment[J]. Environmental Pollution, 2022, 305: 119257. [Article] [CrossRef] [Google Scholar]
- YU Y, SRIVASTAVA A, CANALES S. Conditional LSTM-GAN for melody generation from lyrics[J]. ACM Trans on Multimedia Computing Communications and Applications, 2021, 17(1): 1–20 [CrossRef] [Google Scholar]
- YAO Z, ZHAO C. FIGAN: a missing industrial data imputation method customized for soft sensor application[J]. IEEE Trans on Automation Science and Engineering, 2021, 19(4): 3712–3722 [Google Scholar]
- WANG X. Data preprocessing for soft sensor using generative adversarial networks[C]//15th International Conference on Control, Automation, Robotics and Vision, 2018: 1355–1360 [Google Scholar]
- LIU F T, TING K M, ZHOU Z. Isolation forest[C]//2008 Eighth IEEE International Conference on Data Mining, 2008 [Google Scholar]
- GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Communications of the ACM, 2020, 63(11): 139–144. [Article] [CrossRef] [Google Scholar]
- MIRZA M, OSINDERO S. Conditional generative adversarial nets[J/OL]. (2014-11-06)[2023-02-15]. [Article] [Google Scholar]
All Tables
All Figures
 |
图1 基于GAN的传感器缺失数据生成方法框架图 |
| In the text | |
 |
图2 CGAN数据生成结构图 |
| In the text | |
 |
图3 镍闪速炉熔炼工艺流程图 |
| In the text | |
 |
图4 生成器损失曲线图 |
| In the text | |
 |
图5 判别器损失曲线图 |
| In the text | |
 |
图6 原始数据与生成数据密度分布图 |
| In the text | |
 |
图7 4种缺失数据填充效果图 |
| In the text | |
 |
图8 软测量预测误差箱式图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


