| Issue |
JNWPU
Volume 42, Number 4, August 2024
|
|
|---|---|---|
| Page(s) | 597 - 605 | |
| DOI | https://doi.org/10.1051/jnwpu/20244240597 | |
| Published online | 08 October 2024 | |
Study on fracture of hyperelastic Kirchhoff-Love plates and shells by phase field method
超弹性Kirchhoff-Love板壳的相场断裂研究
1
School of Science, Chang'an University, Xi'an 710064, China
2
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China
3
School of Civil Engineering, Central South University, Changsha 410075, China
Received:
29
May
2023
Thin walled structures such as plates and shells are widely used in many engineering fields. To Predict its fracture behavior is of great significance for integrity design and strength evaluation of engineering structures. Numerical simulation of the fracture behavior of hyperelastic plates and shells is a challenge due to complex kinematic description, hyperelastic constitutive relationship, geometric nonlinearity and the degradation on elastic parameter caused by fracture damage. Combining Kirchhoff Love (K-L) shell theory with the fracture phase field method, and numerically discretizing the first and second order partial derivatives of displacement field and phase field by using T-splines and meeting the requirements of K-L plate and shell theory for the C1 continuity of the shape function, a model for the isogeometric analysis numerical formulation of the phase field fracture in hyperelastic K-L plates and shells is established. The fracture failure behavior of hyperelastic K-L plates and shells under the uniform load and displacement load is simulated, and the effect of the Gaussian curvature on the fracture behavior of hyperelastic K-L shells is studied. The simulation results show that the present numerical scheme can effectively capture the complex crack propagation path of plates and shells under the uniform load, and the displacement field can effectively reflect the crack distribution of materials. The thin shell with negative Gaussian curvature shows the excellent fracture performance under the internal pressure, and can withstand the greater internal pressure.
摘要
板壳这类薄壁结构在诸多工程领域得到广泛应用, 预测其断裂行为对工程结构的完整性设计和强度评估具有重要意义。超弹性板壳断裂行为的数值仿真需同时考虑复杂的运动学描述、超弹性本构关系、几何非线性和断裂损伤对弹性常数的退化, 因此具有一定的挑战性。将Kirchhoff-Love(K-L)板壳理论与断裂相场法结合, 采用T样条对位移场和相场的一、二阶偏导进行数值离散, 满足了K-L板壳理论对形函数C1连续的要求, 建立了超弹性K-L板壳相场断裂模型的等几何分析数值格式, 模拟了超弹性K-L板壳在均布载荷和位移加载下的断裂失效行为, 研究了高斯曲率对超弹性K-L壳断裂性能的影响。数值模拟结果表明: 所建立的数值格式可以有效地捕捉板壳在均布载荷下的复杂裂纹扩展路径, 模拟得到的位移场可以有效地反映材料的裂纹分布情况; 具有负高斯曲率的薄壳在承受内压作用时具有较好的断裂性能, 可以承受更大的内压。
Key words: hyperelastic / plate and shell / phase field / fracture / isogeometric analysis
关键字 : 超弹性 / 板壳 / 相场 / 断裂 / 等几何分析
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
板壳广泛应用于航空、航天、船舶、汽车、土木和可再生能源等工业领域。工程中常用的板壳等薄壁结构往往采用非线弹性的材料, 并且其变形幅度不满足小应变假设。预测非线弹性板壳的断裂行为对于这些工业领域薄壁结构的强度评估具有重要意义。Kirchloff-Love(K-L)壳理论是一种薄板壳理论, 不考虑横向剪切变形的影响, 在数值计算中每个节点仅有3个自由度。相比Reissner-Mindle壳理论, K-L壳的计算成本更低。然而, K-L壳理论需要构造C1连续的形函数。有限元方法的形函数大多基于拉格朗日插值得到, 难以实现相邻单元之间导数的连续(C1连续)[1]。此外, 有限元方法在对曲面进行建模时, 难以精确地表征曲面的几何信息, 会对计算精度造成一定影响。为了对非线弹性薄壁结构的强度进行有效评估, 需要寻求一种既能模拟板壳的断裂行为, 又能满足形函数C1连续要求, 还能对曲面进行有效建模的数值模型。
断裂相场法是一种连续的基于正则化断裂变分理论的计算断裂力学方法, 它将不连续的裂纹近似成光滑的损伤带, 并采用相场来定量描述材料的损伤程度。相比扩展有限元(extended finite element method, XFEM)[2]方法, 它不需要额外的判据, 可以方便地捕捉裂纹的萌生、扩展、分叉和汇合等行为, 并且可以追踪裂纹的扩展路径和模拟复杂的三维裂纹扩展问题[3–8]。
等几何分析[9](isogeometric analysi, IGA)中的非均匀有理B样条函数(non-uniform rational B-splines, NURBS)和其他样条函数可以满足K-L壳的C1连续要求。将等几何分析方法和断裂相场法结合对K-L壳的断裂行为进行模拟能够同时发挥2种方法的优势。对此, 一些学者展开了相关研究。Kiendl等[10]首次将IGA和断裂相场法结合来模拟线性K-L壳的断裂行为。Ambati等[11]建立了基于相场法的IGA实体-壳断裂数值格式, 模拟了弹塑性壳在有限变形下的韧性断裂。Paul等[12]建立了K-L壳的四阶相场断裂模型, 并采用IGA方法对该模型的位移场和相场进行数值求解。Proserpio等[13]基于断裂相场法模拟复杂壳结构的脆性断裂, 采用交错的等几何分析数值格式求解平衡方程和相场演化方程。然而, 上述工作中IGA的数值实现都是基于NURBS函数并未考虑几何非线性。NURBS函数在表征复杂几何形状的壳上具有一定的局限性, 而T样条函数在这方面性能优于NURBS[14–15]。
本文基于开源的Matlab等几何程序[16–17]平台给出了超弹性K-L壳的相场断裂模型数值框架, 推导了相场断裂模型关于位移场和相场的变分形式及其线性化后的表达式, 考虑了几何非线性的效应, 模拟了超弹性K-L壳在不同加载下的断裂行为, 研究了高斯曲率对受内压壳体断裂性能的影响, 以期为薄壁结构的强度评估提供参考依据。
1 超弹性K-L壳理论及相场断裂模型
1.1 超弹性K-L壳的基本理论
如图 1所示, X和x分别表示壳中一物质点在初始构型和当前构型下的位置矢量; Xm和xm分别表示初始构型和当前构型下中性面所对应物质点的位置矢量。X和x用坐标(θ1, θ2, θ3)表示; Xm和xm则用坐标(θ1, θ2)表示。根据Kirchhoff-Love壳理论, X, x和Xm, xm之间存在如下关系[18]
式中, A3和a3分别为不同构型下壳的中性面内点(θ1, θ2)处的单位法向量, 可以表示成
式中, “×”表示叉积。由Green-Lagrange应变张量的定义, 有
式中, Eαβ为Green-Lagrange应变张量的分量; gαβ和Gαβ分别表示初始构型和当前构型下度规张量的分量。本文二阶张量的上下标分别表示逆变协变分量。根据度规张量的定义[18], 有
将(1)式代入(4)~(5)式中, 借助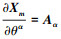
和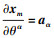
并忽略关于θ3的二次项可以得到度规张量分量的最终表达式, 如(6)~(7)式所示。
将(6)~(7)式代入(3)式中, 可以进一步得到Green-Lagrange应变张量分量的表达式
由于Aα·A3=aα·a3=0, 对等式两边同时关于θβ求偏导, 可以得到
将(9)式代入(8)式中, 可以得到Eαβ的最终表达式[18]
式中：εαβ为壳的膜应变分量, 它描述壳中性面的面内变形, 其几何意义为变形前后中性面第一不变量的变化；καβ为壳的弯曲应变分量, 它描述壳中任意一点相对于中性面曲率的改变, 其几何意义为变形前后中性面第二不变量的变化[18]。
由(4)~(5)式, 有
将(12)式两端同乘以逆变基矢量Gj可以得到
将(13)式代入(11)式中, 进一步有
式中, “⊗”表示张量并矢。根据(14)式和变形梯度的定义, 可以得到壳的变形梯度F具体表达式
右柯西-格林应变张量C可以表示为
由(16)式可以得到C的第一、三不变量
 |
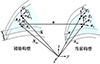图1 初始构型和当前构型下壳的几何描述 |
1.2 K-L壳的相场断裂模型及其变分形式
根据断裂变分原理, K-L壳的势能Π由弹性应变能和断裂表面能组成, 其表达式为
式中: ϕ为相场变量; g(ϕ)为退化函数; ψe为弹性应变能密度; Gc为临界应变能释放率; γ为裂纹密度函数。
为了对该相场断裂模型进行数值求解, 首先需给出总势能泛函的一阶变分形式, 于是有
式中: δ表示变分算符; nαβ, mαβ为壳的内力和弯矩分量, 它们可以表示成
式中：Sαβ为壳中性面内第二P-K应力张量的逆变分量。由(8)、(10)式可以得到膜应变和弯曲应变增量的表达式
根据(1)~(2)式, δaα, β和δa3可以进一步表示为
式中, I为二阶单位张量。为了得到关于K-L壳的相场断裂模型的Hessian矩阵, 需要对(19)式进一步线性化, 便有
由(10)、(20)式, 内力和弯矩分量的线性增量可以分别表示为
式中,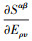 
为本构张量。本文选用的是Neo-Hookean超弹性本构模型, 其应变能表达式为
式中,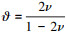 
, ν为泊松比。第二P-K应力Sαβ和本构张量
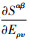分别为
由(21)~(22)式, Δδεαβ和Δδκαβ可以进一步表示成
由(24)式, Δ{δ[a3]}可以表示成
式中，δ|a1×a2|=a3·δa3。对于线性K-L壳, Δδεαβ和Δδκαβ项通常忽略, 即不考虑膜应变和弯曲应变带来的几何非线性。裂纹密度函数γ通常取成如(34)式所示形式。
于是有
式中: ▽ϕ表示相场梯度; δϕ和Δϕ分别表示相场的虚增量和线性增量; δ▽ϕ和Δ[▽ϕ]分别为相场梯度的虚增量和线性增量。
 |
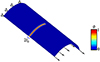图2 相场在K-L壳中的分布 |
2 超弹性K-L壳相场断裂模型的等几何分析(IGA)数值框架
T样条在表征复杂几何形状和局部加密上具有一定优势, 在坐标系(θ1, θ2)上其数学表达式为[15]
式中：Pi是T样条控制点; Ri为有理调配函数; wi为权重; Ni是定义在矩形域内的B样条基函数。T样条的数学表达式与非均匀有理B样条极为相似, 主要区别在于定义域和调配函数。
Bézier通过构建一个矩阵来实现提取操作, 该矩阵将Bézier单元上的Bernstein多项式基映射到全局样条基, 该矩阵转置则是将样条控制点映射到Bézier控制点。对于任意提取的Bézier单元, 物理区域内的调配函数可以表示为[15]
式中：ω表示T样条控制点的权重矢量; T为Bézier提取算符的稀疏矩阵; 矩阵Λ为对角线元素为ω分量的对角矩阵;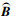 
为Bernstein基函数。由(37)式, 可以推导出调配函数对坐标θα, θβ的偏导
Bernstein基函数及其一、二阶导数可以通过迭代公式进行计算。对于基于T样条的等几何数值离散, 通过Bézier提取得到的每个Bézier单元的位移、虚位移增量、和位移增量、相场、虚相场增量和相场增量可以近似表示为
式中，u和ϕ分别表示由该Bézier单元所有控制点的位移和相场组成的向量。由图 1和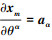
可以得到
由(20)式可以得到
式中：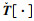
表示矢量算符, 将作用的矢量与其他矢量的叉积表示成一反对称矩阵与其他矢量乘积的形式。为了便于数值实现, 通过Voigt规则将膜应变张量ε和弯曲应变张量κ转化成矢量形式, 由(21)式可以得到δε和Δε的离散形式
由(23)式得
根据(22)、(44)式可以得到δκ和Δκ的离散形式
对于材料非线性项Δnαβδεαβ和Δmαβδκαβ的离散化, 结合(21)~(26)式和(41)~(45)式可得
式中，D为(29)式中四阶本构张量通过Voigt规则转化后得到的矩阵。对于材料非线性项nαβΔδεαβ和mαβΔδκαβ的离散化, 结合(21)~(24)式、(30)~(32)式和(41)~(45)式可以得到
式中，矩阵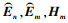
的具体表达式可以参考文献[16, 19]中给出的结果。将(46)~(47)式代入(25)式中可以得到位移场刚度矩阵的表达式
将(43)、(45)式代入(19)式中可以得到位移场残差的表达式
式中，n和m为内力和弯矩张量通过Voigt规则转化后得到的向量。为了构造相场的刚度矩阵和残差需对相场梯度的虚增量和线性增量进行离散化
将(50)式分别代入(25)、(19)式可以得到相场的刚度矩阵和残差
为了有效地对位移场和相场进行数值求解, 忽略位移场和相场的耦合刚度矩阵, 其Newton-Raphson迭代格式为[10]
式中, τ为迭代步数。基于上述的数值格式, 可以实现对超弹性K-L壳的相场断裂求解。数值实现的步骤如下: ①导入几何模型; ②将几何数据转换成网格结构; ③对特定控制点施加边界条件; ④计算组装刚度矩阵和残差, 并根据(52)式对位移场和相场进行迭代求解; ⑤对计算结果进行后处理。
3 数值算例
本节基于K-L壳的相场断裂模型的IGA数值框架, 模拟了方形板的径向、环向断裂, 研究了曲面壳在不同载荷作用下的失效行为。
3.1 均布载荷下方形板的断裂
本节研究方形板在双向弯曲作用下的断裂行为。该方形板四周固支, 边长和厚度分别为2 mm和0.1 mm; 整个板的上表面承受垂直板平面向下的均布载荷, 如图 3所示, 载荷从0逐渐增加到4 MPa。
材料的剪切模量和泊松比分别为8 000 MPa和0.37, 相场长度尺度参数l0为0.2 mm, 临界应变能释放率Gc为0.1 N/mm。采用T样条函数对该方形板进行均匀离散, 单元数为1 225, 节点数为1 024。图 4给出了不同加载阶段z方向的位移云图、相场云图以及文献[10]中对应的裂纹扩展路径。文献[10]研究对象为线弹性板壳。
从图 4可以看出, 在前期加载阶段, 板的损伤区域主要分布在板的中心位置, 随着载荷增加, 板的中心区域出现了“十”字形的裂纹。最终, 板沿2条对角线方向断为四部分。本节数值结果中裂纹的分布特征与图 4b)中的结果吻合较好。
 |
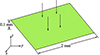图3 方形板的几何尺寸和外载荷 |
 |
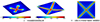图4 模拟结果 |
3.2 圆环板的环向断裂
本节模拟含初始缺口圆环板的径向断裂行为。该圆环板内外边界固支, 圆环区域承受竖直向下的均布载荷, 如图 5所示。
载荷大小从0逐渐增加到3 MPa。四处缺口以中心对称方式排布, 每处缺口对应的圆心角为π/8。板的厚度为0.2 mm, 板的弹性模量和泊松比分别为10 000 MPa和0.37, 临界应变能释放率Gc为0.3 N/mm。为了精确地捕捉裂纹的扩展路径, 对裂纹将要经过区域进行加密, 最小网格尺寸为0.15 m, 相场长度尺度参数l0为0.3 mm。
模拟得到的位移场和相场云图如图 6所示, 分别对应裂纹萌生、裂纹扩展、完全断裂3个阶段。最终, 相邻的裂纹汇聚使得圆环板断为两部分, 裂纹成为均布载荷的加载末端。
 |
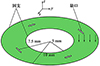图5 圆环板的几何参数和加载条件 |
 |
图6 不同阶段的相场云图 |
3.3 内压作用下旋转曲壳的失效破坏
高斯曲率是表征曲面弯曲程度的重要几何量, 同时它也会对薄壁结构的受力和变形产生影响。为了研究高斯曲率对壳的断裂性能影响, 选取了旋转椭球面壳、圆柱面壳、旋转双曲面壳这三类具有代表性的薄壳结构作为研究对象。它们曲面的高斯曲率分别为正、零和负。为了减小计算量, 选取1/2模型为研究对象, 其关键几何参数如图 7所示。各曲面壳中心处均含有长度为20 mm的初始缺口。各曲面壳与X-Z平面的截面均为直径60 mm的圆。对每个曲壳Y方向两端施加X, Y方向的约束，Z方向端部施加对称边界条件。各曲面壳均承受沿其表面外法线方向的均布内压, 载荷大小从0逐渐增加到0.5 MPa。各曲面壳的弹性模量、泊松比、厚度、临界应变能释放率和相场长度尺度参数均相同, 分别为10 000 MPa, 0.39, 2 mm, 0.06 N/mm和3 mm。
图 8比较了3种曲壳的断裂破坏过程, 给出了裂纹萌生、裂纹扩展和完全破坏3个阶段的相场云图。可以发现, 3种曲壳均是在初始缺口两端发生损伤累积和裂纹萌生, 随后, 萌生的2处裂纹往Y轴两端扩展, 最终薄壳结构发生完全断裂。
图 9对比了3种曲壳的内压-平均环向应力曲线。根据应力分析, 曲壳中任意垂直于Y轴的截面的环向应力与内压存在线性关系。图 9中的3条曲线在破坏发生前很好地符合这一特征。可以发现, 旋转双曲面壳可以承受的内压最大, 圆柱壳和旋转椭球面壳可以承受的内压相等。除此之外, 圆柱壳的平均环向应力峰值最大, 旋转椭球面壳次之, 旋转双曲面壳的平均环向应力峰值最小。
 |
图7 旋转椭球面、圆柱面和旋转双曲面的关键几何参数 |
 |
图8 不同高斯曲率曲壳断裂破坏过程 |
 |
图9 不同高斯曲率曲壳的内压-平均环向应力曲线 |
4 结论
本文建立了超弹性K-L壳的相场断裂模型的IGA求解数值格式, 采用T样条对位移场和相场的相关变量进行离散, 满足了K-L壳理论对位移形函数C1连续的要求。采用建立的数值求解格式, 模拟了超弹性K-L板壳的径向、环向裂纹扩展问题和受内压的破裂问题。数值仿真的结果表明:
1) K-L壳的弹性应变能表示为超弹性自由能, 并考虑几何非线性的影响, 可以有效地重现文献[10]中对线弹性K-L板壳的径向和环向断裂模拟的裂纹扩展特征, 并且发生完全破坏时位移场的分布规律与文献[10]一致, 验证了该数值求解格式的鲁棒性。
2) 该数值求解格式可以模拟竖直方向的均布载荷、位移加载和垂直于外表面的均布载荷下的板壳的断裂破坏行为, 可以捕捉复杂曲面壳的裂纹扩展路径。
3) 相比正、零高斯曲率曲壳, 负高斯曲率曲壳能承受更大的内压, 并且环向应力峰值最小。采用旋转双曲面是作为压力容器的外表面可以一定程度上提高压力容器的强度。
References
- BENSON D, HARTMANN S, BAZILEVS Y, et al. Blended isogeometric shells[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 255, 133–146 [Article] [CrossRef] [Google Scholar]
- DOLBOW J, MOES N, BELYTSCHKO T. Modeling fracture in Mindlin-Reissner plates with the extended finite element method[J]. International Journal of Solids and Structures, 1999, 37, 7161–7183 [Google Scholar]
- WU J Y, NGUYEN V P, NGUYEN C T, et al. Phase-field modeling of fracture[J]. Advances in Applied Mechanics, 2020, 53, 1–183 [CrossRef] [Google Scholar]
- ZHUANG X, ZHOU S, HUYNH G D, et al. Phase field modeling and computer implementation: a review[J]. Engineering Fracture Mechanics, 2022, 262, 108234 [Article] [CrossRef] [Google Scholar]
- FRANCFORT G A, MARIGO J J. Revisiting brittle fracture as an energy minimization problem[J]. Journal of the Mechanics and Physics of Solids, 1998, 4681319–1342 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- BOURDIN B, FRANCFORT G A, MARIGO J J. Numerical experiments in revisited brittle fracture[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(4) 797–826 [Article] [CrossRef] [Google Scholar]
- CHEN Pengcheng, MA Yu'e, PENG Fan, et al. Simulating hydrogen embrittlement fracture based on phase field method[J]. Journal of Northwestern Polytechnical University, 2022, 40(3): 504–511 [Article] (in Chinese) [CrossRef] [EDP Sciences] [Google Scholar]
- YU Yuanfeng, ZHENG Xiaoya, LI Peng, et al. Phase field model of brittle fracture based on polynomial degradation function[J]. Journal of Northwestern Polytechnical University, 2022, 40(5): 980–989 [Article] (in Chinese) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- HUGHES T J, COTTRELL J A, BAZILEVS Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(34/35/36/37/38/39/40/41): 4135–4195 [CrossRef] [Google Scholar]
- KIENDL J, AMBATI M, LORENZIS L, et al. Phase-field description of brittle fracture in plates and shells[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 312, 374–394 [Article] [CrossRef] [Google Scholar]
- AMBATI M, LORENZIS L. Phase-field modeling of brittle and ductile fracture in shells with isogeometric NURBS-based solid-shell elements[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 312, 351–373 [Article] [CrossRef] [Google Scholar]
- PAUL K, ZIMMERMANN C X, DUONG T, et al. Isogeometric continuity constraints for multi-patch shells governed by fourth-order deformation and phase field models[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 370, 113219 [Article] [CrossRef] [Google Scholar]
- PROSERPIO D, AMBATI M, LORENZIS L, et al. A framework for efficient isogeometric computations of phase-field brittle fracture in multipatch shell structures[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 372, 113363 [Article] [CrossRef] [Google Scholar]
- BAZILEVS Y, CALO V M, COTTRELL J A, et al. Isogeometric analysis using T-splines[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(5/6/7/8): 229–263 [CrossRef] [Google Scholar]
- EVANS E, SCOTT M, LI X, et al. Hierarchical T-splines: analysis-suitability, Bézier extraction, and application as an adaptive basis for isogeometric analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 284, 1–20 [Article] [CrossRef] [Google Scholar]
- DU X, ZHAO G, ZHANG R, et al. Numerical implementation for isogeometric analysis of thin-walled structures based on a Bézier extraction framework: nligaStruct[J]. Thin-Walled Structures, 2022, 280, 109844 [CrossRef] [Google Scholar]
- DU X, ZHAO G, WANG W, et al. NLIGA: a MATLAB framework for nonlinear isogeometric analysis[J]. Computer Aided Geometric Design, 2020, 80, 101869 [Article] [CrossRef] [Google Scholar]
- VAN A L. Nonlinear Theory of elastic plates[M]. Oxford: ISTE Press, 2017, 129–155 [CrossRef] [Google Scholar]
- NGUYEN V P, ANITESCU C, BORDAS B, et al. Isogeometric analysis: an overview and computer implementation aspects[J]. Mathematics and Computers in Simulation, 2015, 117, 89–116 [CrossRef] [Google Scholar]
All Figures
|
图1 初始构型和当前构型下壳的几何描述 |
| In the text | |
|
图2 相场在K-L壳中的分布 |
| In the text | |
|
图3 方形板的几何尺寸和外载荷 |
| In the text | |
|
图4 模拟结果 |
| In the text | |
|
图5 圆环板的几何参数和加载条件 |
| In the text | |
|
图6 不同阶段的相场云图 |
| In the text | |
|
图7 旋转椭球面、圆柱面和旋转双曲面的关键几何参数 |
| In the text | |
|
图8 不同高斯曲率曲壳断裂破坏过程 |
| In the text | |
|
图9 不同高斯曲率曲壳的内压-平均环向应力曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.