EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 42 / No 5 (October 2024) JNWPU, 42 5 (2024) 783-792 Full HTML
Open Access
Issue
JNWPU
Volume 42, Number 5, October 2024
Page(s) 783 - 792
DOI https://doi.org/10.1051/jnwpu/20244250783
Published online 06 December 2024

© 2024 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

复合材料组分多样、内部结构空间较之金属结构更为复杂, 在失效过程中常多模式并发, 在同样的载荷工况下, 纤维断裂、基体断裂、层间开裂、分层、脱粘等都有可能同时发生。且实际工程中结构受到材料批次、加工工艺、结构尺寸、载荷等影响, 都会引发失效的不确定性。近年来, 多种方法被应用于复合材料可靠性分析和多模式可靠性分析方面。

复材可靠性问题长久以来都被持续关注, 美国武装部队技术情报局出版了专题为基于概率的复合材料可靠性设计方法的科技报告[1], 报告中收集了美国航天航空局结合大量单层板、层合板、带孔层合板、风力涡轮机叶片等的试验数据建立了复合材料结构可靠性分析流程框架; 美国西南研究院开发了NESSUS软件[2], 该软件已经为美国国家航空航天局(national aeronautics and space administration, NASA)解决了航天发动机部件、汽车结构、管道等多领域的复材可靠性分析问题; 在复材可靠性建模方面, 吴凡等[3–5]结合Hashin、Tsai-Hill准则对纤维、基体断裂等失效模式进行了可靠性模型的构建; 屈曲在承力结构中更容易发生, 结合Kriging[6]、响应面法[7]等建立极限状态方程, 并结合蒙特卡罗[8]、一次二阶矩[9–10]、自适应迭代采样[11]、数值线采样[12]求解可靠度的大小; 连接结构也常常作为可靠性分析的重点, 如单钉连接结构[13]、螺栓连接结构[14]、胶接结构[15]等。在考虑多模式并发的复合材料可靠性分析方面, 李蓝天等[16]同时分析了胶接区域和蒙皮失效对整体壁板结构的影响; Nadjafi等[17]结合有限元仿真和二阶矩法开发了考虑孔损伤和基体开裂和纤维/基体脱粘的可靠性模型; Ma等[18]面向热力耦合, 精确考虑了热应力和温度效应, 实现复合材料层合结构体系的非概率系统可靠性设计优化。为了适应多模式并发的特点, 相关研究通过窄界限理论[19–20]、子集模拟法[21–22]、马尔可夫理论[23–25]、分枝约界法[26–28]等方法对多模式的协同分析进行了探索, 但这类方法在复合材料领域的应用十分有限。

在复合材料性能分析中, 多数研究停留在强度、刚度的校核与试验验证分析, 然而在民用飞机等实际工程中急需相关流程, 考虑实际状态的不确定性, 结合可靠性分析思路, 验证结构能否满足安全性指标或允许失效概率; 在多模式可靠性分析方面, 多数研究对模式的覆盖程度不高, 无法对其多模式的协同分析方法进行推广。因此, 本文提出了分枝约界法, 遍历和筛选复合材料结构的主要失效模式与主要失效位置, 达到保证计算精度的前提下减少计算规模的目的, 并结合复合材料独有的失效准则向安全边界方程进行转换, 为复材加筋板多失效模式可靠性分析方法提供一种新思路。

1 分枝约界法

分枝约界法(branch and boundary method, BBM)是指概率评估体系方法中, 通过遍历思想找出结构、元件所有可能的失效模式和位置, 并结合应力状态、边界条件、结构特征或单一模式失效概率大小等筛选主要失效模式和失效位置, 并计算结构协同可靠度的方法[29–30]。与金属结构不同, 复合材料的失效模式具有并发式的特点, 如图 1所示。进行单一模式分析强度、刚度校核或可靠性分析显然无法衡量真实的结构失效状态, 简单枚举后对所有失效模式进行逐一分析和判断显然会引发建模和计算规模的爆炸。分枝约界法在逐一排查失效模式和失效位置, 保证“算无疑策”的基础上, 结合应力状态、边界条件、结构特征或单一模式失效概率大小对失效模式和其对应的多位置进行剪枝和约界, 达到筛选主要失效模式和位置、协同化分析多模式可靠性、关注薄弱环节、减少计算规模的目的。

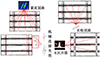thumbnail 图1

复合材料壁板结构多模式和多位置失效并发示意

1.1 分枝原则

复合材料组分复杂, 由纤维和基体共同组成。Hashin失效准则、Pinho失效理论、Puck失效理论等将纤维和基体的失效区分开, 尤其是Hashin中还会区别纤维/基体拉伸、压缩破坏、层间开裂和剪切破坏等。纤维和基体相对于整体复合材料为细观尺度, 因此遍历这类失效模式的过程称为“细观”失效模式分枝。除此之外, 还有一些失效模式是复合材料结构的整体失效, 较为典型的有屈曲、脱粘、整体断裂等, 将该过程称为“宏观”失效模式分枝。

除了失效模式多变以外, 复合材料具有不均匀性, 内部孔隙分布不均, 因此, 失效的位置变化多样, 这也是其失效状态具有不确定性的重要原因。对失效模式进行第一层级分枝后, 针对各个失效模式逐步分析, 得到第二层级“多失效位置”分枝。经过这样的2次迭代共同遍历了复合材料结构全部可能的失效状态, 如图 2所示。

thumbnail 图2

复合材料分枝原则示意

1.2 约界原则

复合材料的多失效模式并发是常态, 但受到结构特征、细节布置、应力状态等原则的限制, 部分失效模式会最先被引发, 而其余失效模式则应当被筛选掉, 称该过程为“约界”。约界的原则可分为定性约界和定量约界。定性分析中通常根据应力状态进行判断：如以应力状态或边界条件等为约束对失效模式进行约界, 如剪切破坏总发生在纤维方向应力为负的状态下, 若应力状态为正则可对其进行约界；以结构特征等为原则可对失效位置进行约界, 如薄蒙皮壁板的总体屈曲总发生在局部屈曲以后、桁条与壁板边缘距离较小的壁板屈曲位置发生在桁条之间等。定量分析, 直接根据最危险部位在单一失效模式下的失效概率大小约界。复合材料各主要失效模式和失效位置间相互独立, 最终建立复合材料结构可靠性协同模型如(1)式所示。不相互独立的模式和位置原则上应当在前述约界过程中通过相互比较而被筛选。

2 复材结构可靠性分析方法

随着复合材料在民用飞机上的大量推广和应用, 基于概率统计的可靠性分析研究对于复合材料结构具有重要意义。一是航空结构尤其是民航结构的安全性要求极高, 需要尽可能预测或判断发生故障的可能性; 二是相比于金属结构, 复合材料的变异因素更多, 而传统确定性设计存在一定的局限性, 如无法量化可靠性大小, 安全系数源于过去经验且设计结果过于保守。复合材料可靠性分析以失效理论作为基础, 引入概率设计的思想。本节结合分枝约界法探索多失效模式、多位置的复合材料结构可靠性分析研究, 形成复合材料可靠性分析统一的流程与框架。

2.1 失效准则与安全边界方程

结合复合材料特有的失效准则构建单一失效模式下的复合材料结构可靠性模型。复合材料常见失效准则及其可靠性模型如表 1所示, 以此建立模量、强度、载荷等力学性能参数与壁板可靠度之间的函数关系。

表1

常见的复合材料单一失效模式可靠性建模

2.2 复材结构多模式可靠性分析方法

民用飞机机体结构静强度验证是保证飞机结构安全的基础。结合载荷、材料、性能参数的分散特性进行复合材料结构静强度可靠性分析是民用飞机典型结构允许失效概率制定和适航验证的重要依据。要鉴定结构的安全性, 就必须全面涵盖其可能发生的失效状态, 并结合分枝约界法筛选主要模式与位置, 减少计算规模。对主要失效模式及其失效准则中涉及的力学响应，通过仿真、工程算法、理论推导、试验等方式获得其均值和分散特性, 结合蒙特卡罗方法对安全边界方程进行求解, 最终求得给定载荷水平下的复合材料结构可靠度。基于分枝约界法的复材结构多模式可靠性分析框架如图 3所示。

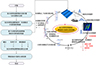thumbnail 图3

基于分枝约界法的复材结构多模式可靠性分析方法

3 案例验证

3.1 复材加筋板基本信息

复合材料加筋结构最终显现出的失效模式很大程度上取决于其结构特征。结构件的试验总是被重复4~5次, 并以该结果作为强度、刚度校核的比对目标。但从适航符合性的角度来说, 这样的方法无法满足安全性分析的技术条件。结合相关适航条款, 民用飞机典型承力结构其失效概率不应大于10-7, 也就是说, 从理论上来说其应当结合数值模拟或仿真手段被模拟107次以上, 才能够被确认是否满足安全性指标要求。因此, 随着复合材料结构在民用飞机上的大量应用, 其也应当和金属结构、系统一样, 即其潜在的失效模式不应当因在4~5次的试验当中没有出现而被忽略。结合可靠性的设计思路考虑载荷、力学响应和结构本身的分散特性, 分析结构所有的潜在风险。本文基于分枝约界法, 开展轴向压缩载荷下的复合材料加筋结构多模式、多位置可靠性分析。加筋板物理建模与数据参考了文献[31]中的四筋条复合材料T型加筋板模型, 加筋板外形尺寸如图 4所示, 铺层信息见表 2，材料属性见表 3~4。

thumbnail 图4

复合材料T型加筋板几何尺寸
表2

复合材料铺层

表3

CF3011/BA9916属性

表4

胶膜属性

3.2 基于BBM的复材加筋板主要失效模式与位置分析

根据加筋结构的组成和受载特点, 先开展“分枝”, 遍历复材加筋板所有可能的失效模式。首先是“细观”分枝, 在压缩载荷下, 加筋结构可能会直接压溃断裂, 即蒙皮纤维断裂、蒙皮基体断裂、长桁纤维断裂、长桁基体断裂, 当该现象发生在长桁端部时, 还可能同时引起R区开裂; 对“宏观”分枝来说, 屈曲是轴压载荷下最易引发的失效模式之一; 界面失效在宏观中被考虑, 对不含机械连接的加筋结构来说, 蒙皮和长桁之间脱粘是最为典型的界面失效，最后整体壁板压溃。“分枝”如图 5所示。

本文模型中采用的加筋板其蒙皮稍弱于长桁, 其破坏过程一般先发生局部屈曲, 然后是纤维基体局部断裂, 最后是完全破坏或脱粘。试验结果表明, 其在完全破坏后只有界面脱粘轻微发生。取其线性屈曲载荷作为屈曲破坏的失效模式, 取法保守, 但更符合民用飞机设计的基本原则。文献[31]中给出了线性屈曲和最终破坏的试验载荷结果, 试件试验中在865 kN的载荷下蒙皮和长桁发生局部屈曲, 1 280 kN发生完全折断。故结合发生历程和结构特征可约界“壁板总体屈曲”、“蒙皮长桁脱粘”; 结合应力状态, 在轴压载荷下, 基体更为薄弱, 可约界“壁板总体压缩破坏”、“蒙皮纤维断裂”、“长桁纤维断裂”、“长桁R区开裂”、“长桁层间开裂”等, 如图 6所示。对主要失效模式及其位置进行单一与协同可靠性模型构建, 如表 5所示。

与强度、刚度校核不同的是可靠性分析的目的是判断结构在设计载荷下, 能否保持其结构完整性, 保证其抵抗受载的能力。本文以线性屈曲载荷865 kN/1.5=577 kN为载荷水平, 计算在该受载状态下的可靠性。其中, 蒙皮与长桁屈曲载荷来自于文献[31]的试验数据, 其均值为865 kN, 变异系数1.2%;载荷均值为577 kN, 变异系数10%[32]; 强度数据均值如表 3所示, 变异系数5%;应力响应通过仿真手段计算, 计算结果见第4节，作为力学响应的均值, 变异系数5%。各参数均服从正态分布。

thumbnail 图5

加筋板轴压载荷下失效模式与位置分枝图
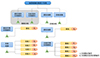thumbnail 图6

加筋板轴压载荷下失效模式与位置约界图
表5

轴压载荷下复合材料加筋板可靠性模型构建

4 结果与讨论

对主要失效模式和失效位置中涉及到的参数变量, 结合试验数据、有限元仿真及数值解析手段进行可靠度求解。首先需要通过有限元分析求得复合材料加筋结构在577 kN轴压载荷下的应力、应变等力学响应值和可靠性方程中涉及到的参数，如表 6所示。

基于Monte Carlo法对建立的可靠性模型进行求解, 各主要失效模式可靠度指标如表 7所示。蒙皮和长桁其单层包含2类材料体系——织物和单向带，多失效模式力学响应如图 7所示。轴压载荷下的复合材料加筋板多模式可靠度求解如(2)式所示。

可靠度分析结果表明, 蒙皮内部发生微小裂痕远早于屈曲的发生, 轴压载荷下加筋板多模式可靠度为0.998。本文的计算结果偏保守, 将损伤起始即作为失效的判断, 这是为了贴合民用飞机设计最为保守的一种情况。若要考虑渐进损伤, 将所有层全部发生失效作为判断复合材料结构失效的标准, 应当代入各层的应力响应, 并取其最小值。

表6

可靠度求解的需求参数

表7

可靠度指标

thumbnail 图7

复合材料加筋结构多失效模式力学响应

5 结论

1) 复合材料的失效模式呈现并发式发生的特点, 多模式可靠性分析更符合其失效的真实状态, 民用飞机复合材料的适航符合性验证中也要求能够识别其潜在的失效模式, 并根据综合性、协同性分析计算其可靠度的大小;

2) 分枝约界法可以结合结构组成、承载状态“分枝”, 找出所有可能的潜在失效模式, 再结合结构特征、应力状态及时“约界”, 本案例中通过采用分枝约界法使计算规模减少75%;

3) 可靠度分析结果表明, 蒙皮内部发生微小裂痕远早于屈曲的发生, 轴压载荷下加筋板多模式可靠度为0.998。

References

  1. CHAMIS C C, SHIAO M C. IPACS(integrated probabilistic assessment of composite structures): code development and applications[C]//Third NASA Advanced Composites Technology Conference, 1993: 7046 [Google Scholar]
  2. SU Changqing, DONG Enguo, QU Ligang. Reliability analysis of square plate based on NESSUS[J]. Mechanical Engineer, 2016(3): 75–77 (in Chinese) [Google Scholar]
  3. WU Fan, TAN Zhiyong, CHEN Qiang, et al. Reliability assessment of composite structures based on local adaptive agent model[J]. Journal of Southeast University, 2023, 53(1): 30–36 (in Chinese) [Google Scholar]
  4. LIU Chenglong, ZHOU Jinyu, QIU Rui. Occurrence function method for reliability analysis of composite laminates[J]. Journal of Mechanical Engineering, 2019, 55(4): 67–74 (in Chinese) [Google Scholar]
  5. SHUVO I I. Hollow canola-wood thermoset composites from concept to completion: fabrication, performance, failure and reliability analysis[J]. SN Applied Sciences, 2020, 12(2): 2087 [CrossRef] [Google Scholar]
  6. DING Zhendong, LI Hongshuang, GUAN Xiaole. Reliability analysis of fuselage skin composite sandwich structure based on agent model[J]. Journal of Northwestern Polytechnical University, 2022, 40(2): 360–368 [Article] (in Chinese) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. ZHANG Guo, LIU Yuchen, ZHANG Xiaowen, et al. Reliability analysis of composite gas cylinder with defective inner liner buckling based on response surface method[J]. Journal of Computational Mechanics, 2023, 40(2): 175–180 (in Chinese) [Google Scholar]
  8. CERVAN D, CORONADO A M, JAIME L Y. Cluster-based stratified sampling for fast reliability evaluation of composite power systems based on sequential monte carlo simulation[J]. International Journal of Electrical Power & Energy Systems, 2023, 147: 108813 [Google Scholar]
  9. ZHANG Nan, SHI Yaoyao, CHEN Zhen, et al. Reliability prediction of chattering in side milling of integral leaf disk[J]. Journal of Northwestern Polytechnical University, 2021, 39(1): 111–118 [Article] (in Chinese) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. PEI Y F S. Lubrication reliability analysis of spur gear systems based on random dynamics[J]. Tribology International, 2021, 153(1): 106606 [CrossRef] [Google Scholar]
  11. ZHANG F, WU M, HOU X, et al. Post-buckling reliability analysis of stiffened composite panels based on adaptive iterative sampling[J]. Engineering with Computers, 2022, 38(4): 2651–2661 [CrossRef] [Google Scholar]
  12. SHI B, DENG Z. An efficient reliability method for composite laminates with high-dimensional uncertainty variables[J]. Acta Mechanica, 2021, 232: 3509–3721 [Article] [CrossRef] [Google Scholar]
  13. ZHANG Jiumin, GU Rujia, LI Hongshuang, et al.. Reliability analysis of composite joint structures based on response surface method[J]. Journal of Computational Mechanics, 2016, 33(5): 711–716 (in Chinese) [Google Scholar]
  14. GAO Kuiyin, LI Haibo, WU Jianguo, et al. Reliability analysis of bolted structures of 2D-C/SiC composites[J]. Strength and Environment, 2020, 47(1): 33–40 (in Chinese) [Google Scholar]
  15. HAN Zijian, ZHOU Jinyu, ZHUANG Bailiang, et al. Reliability analysis of single-lap glued structures for composite parts[J]. Mechanical Design and Manufacturing, 2023, 385(3): 63–66 (in Chinese) [Google Scholar]
  16. LI Lantian, ZHAO Xun. Reliability analysis of composite reinforced plates with multiple failure modes[J]. Journal of Hunan University of Science and Technology, 2017, 32(2): 52–57 (in Chinese) [Google Scholar]
  17. NADJAFI M, GHOLAMI P. Reliability study of notched composite laminates under uniaxial loading based on continuum damage mechanics approach[J]. Iranian Journal of Science and Technology: Transactions of Mechanical Engineering, 2022, 46(4): 911–925 [Article] [CrossRef] [Google Scholar]
  18. MA Y, WANG X, ZENG Let al.. Thermal-mechanical coupling-oriented system reliability optimization of composite structures[J]. Composite Structures, 2021, 270(2): 114107 [CrossRef] [Google Scholar]
  19. LIN Hong, CHEN Guoming. Structural reliability analysis of aging platform considering multiple failure modes[J]. Journal of China University of Petroleum, 2010, 34(4): 107–112 (in Chinese) [Google Scholar]
  20. YIN H, ZHANG D, ZHANG J, et al. Reliability analysis on multiple failure modes of underground chambers based on the narrow boundary method[J]. Sustainability, 2022, 14(19): 12045 [Article] [CrossRef] [Google Scholar]
  21. QIAN Huaming, HUANG Tudi, HUANG Hongzhong, et al.. Structural reliability analysis method with small failure probability and multiple failure mode correlation[J]. Chinese Science, 2022, 52(2): 54–64 (in Chinese) [Google Scholar]
  22. FENG K X, LU Y X, LU Z Z, et al.. Estimation of failure probability-based-global-sensitivity using the theorem of Bayes and subset simulation[J]. Probabilistic Engineering Mechanics, 2022, 70: 103349 [Article] [CrossRef] [Google Scholar]
  23. ZHAO Zhicao, WU Hui, ZHENG Fengzhu, et al.. Reliability modeling and analysis of optoelectronic systems with multiple failure modes[J]. Applied Optics, 2022, 43(4): 635–640 (in Chinese) [CrossRef] [Google Scholar]
  24. FENG Yunwen, LIU Kuijian, XUE Xiaofeng, et al.. Joint optimization of spare parts and redundancy for redundant systems based on Markov process[J]. Systems Engineering and Electronics, 2019, 41(4): 919–928 (in Chinese) [Google Scholar]
  25. HUANG He, WANG Xiaoxu, ZHAO Chunhui, et al.. Adaptive interactive multi-model tracking algorithm based on a posteriori information correction[J]. Journal of Northwestern Polytechnical University, 2011, 29(6): 829–833 (in Chinese) [Google Scholar]
  26. Feng Jinrong. Extended life analysis and inspection cycle formulation for typical multi-crack structure of aircraft[D]. Xi’an: Northwestern Polytechnical University, 2023 (in Chinese) [Google Scholar]
  27. HUANG Xiaoli, GAO Yuelin, XIE Jinxiaoet al.. A new branch-and-bound algorithm for quadratically constrained quadratic programming problems[J]. Applied Mathematics, 2021, 34(1): 240–252 (in Chinese) [Google Scholar]
  28. BING Y, JUAN F H. Study on evaluation method using spline approximation[J]. Journal of Systems Engineering, 2002, 17(3): 261–265 [Google Scholar]
  29. GAO Kai, LIU Gang. Effective intensity improvement of global critical intensity branch-and-bound method[J]. Journal of Jilin University, 2021, 51(2): 597–603 (in Chinese) [Google Scholar]
  30. XIE Wei, ZHANG Yadan, MA Zehuaet al.. Study on the main failure modes of typical five-hole structures based on the branch-and-approximate boundary method[J]. Journal of Northwestern Polytechnical University, 2022, 40(6): 1204–1211 [Article] (in Chinese) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. LIN Guowei, LI Xinxiang. Analytical method and experimental validation of post-buckling analysis of composite reinforced plates[J]. Journal of Aerospace Materials, 2021, 41(4): 149–156 (in Chinese) [Google Scholar]
  32. WU Tangzhen, XIONG Xin, ZHAO Jiang. Research on confidence analysis and revision technique of measured loads based on t-test[J]. Helicopter Technology, 2017, 191(1): 25–30 (in Chinese) [Google Scholar]

All Tables

表1

常见的复合材料单一失效模式可靠性建模

In the text
表2

复合材料铺层

In the text
表3

CF3011/BA9916属性

In the text
表4

胶膜属性

In the text
表5

轴压载荷下复合材料加筋板可靠性模型构建

In the text
表6

可靠度求解的需求参数

In the text
表7

可靠度指标

In the text

All Figures

thumbnail 图1

复合材料壁板结构多模式和多位置失效并发示意
In the text
thumbnail 图2

复合材料分枝原则示意
In the text
thumbnail 图3

基于分枝约界法的复材结构多模式可靠性分析方法
In the text
thumbnail 图4

复合材料T型加筋板几何尺寸
In the text
thumbnail 图5

加筋板轴压载荷下失效模式与位置分枝图
In the text
thumbnail 图6

加筋板轴压载荷下失效模式与位置约界图
In the text
thumbnail 图7

复合材料加筋结构多失效模式力学响应
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.