EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 1 (February 2025) JNWPU, 43 1 (2025) 189-199 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 1, February 2025
Page(s) 189 - 199
DOI https://doi.org/10.1051/jnwpu/20254310189
Published online 18 April 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

舰艇生活区域舱室布局设计是一个多目标优化问题[1], 是舰艇整体系统设计的重要组成部分之一。对舰艇功能舱室进行合理的布局划分, 不仅可以为作业人员提供较为舒适的生活环境, 也有助于舰艇系统效能的发挥, 减少人员作业时的移动距离和时间, 确保物资和工具的高效流通。

随着海洋科技的发展, 传统的设计方法已经无法满足舱室布局的设计需求, 针对此类布局优化问题的研究也愈加广泛。叶聪等[2]基于人机工效学, 综合考虑设备稳定性、兼容性与可达性等方面展开载人潜水器舱内布局设计研究, 阐述以人机功效学为导向的舱内布局设计流程。Chen等[3]以人员操作姿态和性能为驱动, 提出了多种载人舱室布局设计方法, 并构建载人舱室的人体工程学设计指标体系。本文基于Web of Science核心数据库与中国知网数据库, 以“船舶舱室(ship cabins)”和“布局优化(layout optimization)”作为关键词, 检索自2018年1月1日至今的相关中英文文献。对于典型船舶舱室内部布局优化问题, 更多学者采用智能算法进行数学问题求解[4–5]。蔡薇等[6–7]通过定义大型游轮总体布置的特征属性, 建立乘客舱室布局优化模型和无障碍客舱配置模型, 实现舱室布局和家具布局优化。冯青等[8]综合考虑了舰艇居住舱室的特殊性, 量化布局需求, 将能量法引入NSGA-Ⅱ算法进行舱室布局优化。鲍萌等[9]同时考虑舱室和通道布局, 采用遗传算法进行综合布局优化。Wang等[10–11]根据多层船舶舱室布局特点, 分别提出了改进的禁忌搜索遗传算法和改进的遗传帝王蝶优化算法, 有效提高了智能布局算法求解性能。Li等[12]借鉴FLP问题求解思路, 考虑到船舶人流和物流量化后的不确定性, 引入一种双层嵌套的区间优化系统, 为船舱布局提供可行指导。Wang等[13]提出一种基于整数规划的交互式船舶舱室布局优化方法, 并利用人群模拟进行方案的布局质量评价。

由于舰艇生活区域存在共同性, 本文以多层潜艇生活舱室布局问题作为研究对象, 采用多种群遗传算法进行布局优化, 提出一种综合考虑舱室间的邻接需求、流通需求以及应急逃生需求的布局优化方法, 进行仿真设计, 验证方法的有效性。

1 舰艇生活区域布局优化模型

1.1 生活舱室平面布局

本文以潜艇生活舱段的2层典型生活舱室为研究对象。由于潜艇截面特殊性, 舱壁与壳体之间的关系影响到了立体空间尺寸的变化, 舱室舾装工作完成后, 其平面可以近似地视为矩形, 因此, 本文对生活舱段进行简化处理如图 1所示。X轴代表船长方向, Y轴代表船宽方向, 以2层布局优化范围的左下角点作为坐标原点, 纵向通道将同层待布置范围划分为若干布局行, 横向通道将布局行划分为若干待布置区域, 每个区域分别布置一定数量的舱室。由此可以得到1个舱室排序数列, 本文将舱室排列顺序编码和各舱室长宽尺寸作为设计变量, 直至找出最优舱室序列进行布局优化。

thumbnail 图1

生活舱室简化平面布局

1.2 评价目标分析

为更好地实现智能布局, 需要分析各类舱室之间的相关性, 并将设计经验与设计原则以数学方式表达[10]。本文从舱室相对位置关系[14–15]和应急逃生需求角度进行目标分析, 其中相对位置关系包括2个舱室之间的功能邻接强度和人员物资流通强度, 应急逃生需求则考虑了在紧急状态下各层舱室人员通过舱门离开本舱段行至相邻舱段的距离关系。

1.2.1 相对位置关系

对于生活舱室的相邻关系, 设计规范和标准进行了定性描述, 例如居住舱室和医疗室、厨房和餐厅的相对位置等。而舱室间流通关系主要考虑在日常活动时各待布舱室之间人员物资流通需求[15], 在一些舱室之间, 规范中虽然没有明确要求, 但实际存在一定的人员流通关系, 因此需要结合设计需求和专家建议进行判断, 例如居住舱室、活动室和餐厅之间存在一定的流通关系。邻接强度和流通强度就是对2个舱室之间的邻接关系和流通关系的量化表示。现有研究中借鉴了车间设备布局中的概念, 对邻接强度和流通强度进行了5级划分, 如表 1所示。

表1

舱室邻接强度和流通强度等级定义

为了更加科学地表达舱室之间的邻接需求和流通需求, 本文引入模糊评价方法[16], 以扩充邻接强度和流通强度等级数量。首先根据表 1中的描述建立需求评价集U, 即{非常高(1), 较高(0.75), 一般(0.50), 较低(0.25), 无(0)}, 包含5个语言变量, 在下文的计算过程中U=[1, 0.75, 0.50, 0.25, 0]。再根据设计规范和经验梳理不同舱室之间的邻接需求和流通需求程度, 确定相关隶属度矩阵R, 如(1)式所示, 其中, rij表示第i个舱室和第j个舱室之间的强度隶属度, 并且i≠j。

(1) 式中“*”表示无此项。由邻接强度隶属度矩阵Ra、流通强度隶属度矩阵Rc和需求评价集U, 可以定义舱室邻接强度矩阵A和流通强度矩阵C

式中: k表示待布置舱室数量; i和j表示舱室序号; aij表示舱室i和舱室j之间的邻接强度系数; cij表示舱室i和舱室j之间的流通强度系数; rija表示第i个舱室和第j个舱室之间的邻接强度隶属度, rijc表示第i个舱室和第j个舱室之间的流通强度隶属度。当aij=1时, 表示舱室间邻接需求非常大或必须紧邻布置, 当aij=0时表示舱室间无邻接需求; 当cij=1时表示舱室间人员流通关系非常高, 当cij=0时表示舱室间无人员流通, A和C中均不存在舱室对自身的强度关系。

1.2.2 应急逃生距离

舰艇系统的复杂性主要体现在结构复杂、空间狭窄、人员与设备较多[17], 舰艇的疏散能力也受到舱室布局的影响, 如出口宽度、出口位置、舱室位置等。由于潜艇的特殊环境, 当航行期间艇上出现紧急情况, 如火灾、漏水等, 会将相邻舱门关闭进行封舱, 把人员疏散到其他舱段。因此, 本文引入应急逃生距离作为优化评价目标, 通过判断每个舱室几何中心到达船首和船尾2个舱门的距离, 取所有舱室到达同层舱门距离最短路径之和, 其函数表达式为

式中: xi, yi表示舱室i的位置坐标; xh, yh表示船首方向舱门的位置坐标; xs, ys表示船尾方向舱门的位置坐标; k表示待布舱室数量。

1.3 构建数学模型

1.3.1 设计变量及舱室间距离矩阵

根据简化平面中待布舱室的相对位置, 本文将其序号和对应的长宽数值形成的序列X作为设计变量, 需要在平面模型的各布局位置依次对应一个待布舱室序号, 由待布舱室数据以及布局位置顺序可以形成舱室序列, 表达式为

式中: xk表示已布置的舱室序号, lk表示该舱室的纵向长度尺寸, wk表示该舱室的横向宽度尺寸。在检验k个待布舱室形成的舱室序列X时, 需要在平面中确定该序列中两两舱室之间的距离dij, 其方法与1.2.2节相同, 取舱室简化布局几何中心作为舱室位置坐标, 取通道中线进行节点连接, 如图 2所示。

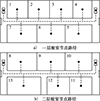thumbnail 图2

舱室节点路径图

舱室对的直线距离路径可以视为两点之间的距离。距离矩阵D的表达式为

式中: dij表示舱室i和舱室j之间的直线距离总长。当舱室对位于同层时, 只需以横纵坐标进行距离计算; 当舱室对位于不同层时, 需要通过竖向梯道连接, 此时对船首方向和船尾方向的梯口进行判断, 取总长较小的梯道坐标代入后续计算。现有文献中坐标值均为固定值, 最终得到的序列解映射到平面后, 各舱室坐标与初始平面模型相同, 这样无法进行应急逃生距离优化, 因此本文中坐标以各舱室长宽尺寸与通道宽度表示, 并对各舱室长宽尺寸进行约束, 将在1.3.3节中进行详细说明。

1.3.2 目标函数

根据前文对舱室相对位置关系的分析, 舱室间邻接强度与流通强度越大, 要求2个舱室相隔的位置越近, 可以分别定义邻接强度目标函数和流通强度目标函数[15], 表达式为

式中, A和C分别为前文定义的邻接强度矩阵和流通强度矩阵, D为X序列下的舱室间距离矩阵。结合应急逃生距离函数, 要求应急疏散效率越高, 各舱室逃生距离总长越小, 因此总目标函数为

式中: ω1, ω2, ω3分别表示邻接强度目标函数、流通强度目标函数和应急逃生目标函数的权重系数, 且ω1+ω2+ω3=1。

1.3.3 布局约束

根据本文确定的目标函数, 定义2类布局约束, 分别为布局区域的面积约束和优化范围的尺寸约束。通道将舱段划分为多个区域, 进行布局优化可视为将待布舱室依次布置到各区域中, 待布舱室的最小面积可以由设计标准和设计经验确定, 要求每个待布区域内的舱室面积之和小于或等于该区域面积。舱室尺寸约束要求各区域内的舱室纵向长度之和小于舱段待布置范围总长, 且同层各布局行内的舱室横向最大宽度与通道宽度之和小于舱段待布置范围的宽度, 保证中心坐标变化时待布舱室不会超出布置区域, 约束表达式为：

式中: Sn, p表示区域p所布置的舱室面积; pn表示待布区域p需要布置的舱室数量; Sp表示区域p的面积; ln, q表示布局行q所布置的舱室纵向长度; qn为布局行q所布置的全部舱室数量; Vl, q表示分割布局行q的横向通道宽度之和; L表示舱段整体优化范围的纵向总长; Wn, d表示d层生活区域的第n行布局内所布置舱室的横向宽度集合; kn表示d层包含的布局行数量, Vd表示d层生活区包含的纵向通道宽度之和, Wd则表示d层整体优化范围的横向总宽度。

2 多种群遗传算法适应性改进

本文定义了布局优化目标、设计变量和布局约束, 从而得到舰艇生活区域舱室布局优化的数学模型。为实现舱室布局优化, 本文采用了多种群遗传算法(MPGA)进行优化计算, 并在其框架基础上进行适应性改进。多种群遗传算法突破了遗传算法(GA)仅靠单个群体进化迭代的框架, 是一种基于多个种群的并行优化算法[18]。本节将详细介绍算法流程和框架要素。

2.1 算法流程

遗传算法作为一种启发式算法, 在搜索空间中以隐含的并行方式工作, 寻找最优解, 广泛应用于布局规划问题[19]。标准遗传算法流程如图 3所示, 利用每一次迭代逐渐进化出更优的近似解。然而标准遗传算法容易出现局部收敛或未成熟收敛现象, 为了避免这一问题, 许多学者对算法进行了改进, 从而提高遗传算法的性能[20–21]。

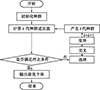thumbnail 图3

标准遗传算法流程

本文针对潜艇舱室布局优化问题, 引入多种群遗传算法, 采用多层编码方式, 并对遗传算子进行适应性改进。多种群遗传算法的各种群之间相对独立, 可以设置不同控制参数使多个种群协同进化[22]。种群之间由移民算子实现个体交换, 通过人工选择算子保存种群每次进化得到的最优个体, 形成精英种群, 兼顾算法的全局搜索和局部搜索, 算法流程如图 4所示。

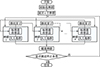thumbnail 图4

多种群遗传算法流程

2.2 算法分析

2.2.1 编码

标准遗传算法一般使用单一编码方式表示每个个体, 通常使用二进制编码表示, 但是这种方式很难准确描述舱室布局优化问题的解空间。因此, 本文采用多层编码方式[23], 编码机制如图 5所示。种群每个个体都包含3个子串, 即表征舱室布局顺序的序号xk、舱室纵向长度lk和舱室横向宽度wk。

thumbnail 图5

个体编码机制

2.2.2 选择算子

本文采用轮盘赌选择方法, 即个体被选中的概率与其适应度大小呈正比。首先选出符合约束的正常个体xi(i=1, 2, …, n), n为群体总数, 记录其适应度f(xi), 其次计算出这些个体被选中的概率 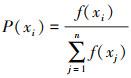, 以及每个个体的累计概率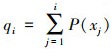; 从[0, 1]范围内生成随机数r, 若r＜q(1), 则选择个体1, 否则选择个体k, 使q(k-1)＜q(k)成立。最后重复以上步骤n次得出新的种群。

2.2.3 交叉算子

交叉算子决定算法全局搜索能力, 各个种群取不同的交叉概率, Pc=0.7+(0.9-0.7)rand(NZQ, 1), 即在[0.7, 0.9]范围内随机产生交叉概率。将染色体根据序号-长度-宽度方式进行匹配, 并根据待布舱室数量进行分组, 如图 6所示。本文规定3种交叉方式(组内交叉、染色体内交叉和染色体间交叉), 在交叉过程中选中2条染色体后随机选择2种方式进行交叉, 具体内容如下:

thumbnail 图6

染色体基因分组

1) 组内交叉, 选取1个个体, 在该个体n个分组中选取1组, 进行随机排序, 得到新的子代个体;

2) 染色体内交叉, 选取该个体内n组中的2组, 若其长度相同, 则互换位置, 得到新的子代个体;

3) 染色体间交叉, 选择2条父代染色体, 序号基因不变, 每隔1组交叉长度和宽度取值, 得到新的子代个体。

2.2.4 变异算子

变异算子决定算法的局部搜索能力, 不同种群取不同变异概率, Pm=0.01+(0.1-0.01)rand(NZQ, 1), 即在[0.01, 0.1]范围内随机产生变异概率, 本文采取的变异策略是随机选取3条染色体, 对第1条染色体随机选择2个舱室序号互换位置; 对第2条染色体随机选则1个舱室调整长度值, 调整范围在(-0.5, 0.5);对第3条染色体随机选择1个舱室调整宽度值, 调整范围在(-0.5, 0.5)。

2.2.5 移民算子

各个种群之间通过移民算子产生联系, 实现多种群的协同迭代, 在每次迭代过程中, 选取种群中的最优个体进行移民, 将目标种群中的最劣个体替换成移民个体。

2.2.6 人工选择

每次进化后, 由人工选择算子在各种群中选取最优个体, 形成由每代最优个体组成的最佳种群, 即精英种群[24], 精英种群的目的是保护各种群的最优个体在进化过程中不遭到破坏或丢失, 因此该种群不进行选择、交叉、变异等操作。

3 仿真案例设计分析

本节利用提出的布局优化模型和算法进行仿真设计研究, 基于图 7所示的2层潜艇生活区进行功能舱室布局优化设计, 该布局中共有17个待布置舱室和船首船尾方向2处上下行梯道, 为方便模拟计算将舱门设置在水平中线位置, 通道宽度为1 m且位置固定, 算法程序运行在MATLAB R2022b平台, 运行环境为Windows 11。

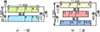thumbnail 图7

2层潜艇生活区初始平面图

3.1 仿真参数设置

建立2层潜艇生活区平面模型, 划分为5个区域, 各个区域初始布局如图 7所示, 计划布置17个主要舱室。对待布舱室进行编号, 其基准面积和匹配的基准尺寸如表 2所示。舰艇舱室作为密闭空间, 设计时应考虑其适人性因素, 为了使空间舒适度更高, 本文将长宽比设置为6∶4[5], 并根据其基准面积进行相应分配。

表2

舱室信息

根据相关设计规范、现有文献和专家建议, 结合潜艇的实际需求, 综合分析后得出17个待布舱室的邻接强度隶属度矩阵Ra和流通强度隶属度矩阵Rc, 代入(2)式中分别得到邻接强度矩阵A和流通强度矩阵C为

由舱室平面布局模型得到的舱室信息、舱室间邻接强度和流通强度的分析结果, 构建本次仿真舱室布局优化的数学模型，如(10)式所示。

式中: n表示通道宽度, 本文中通道宽度取值为1 m; ω1, ω2, ω3分别设置为0.4, 0.4和0.2。本次仿真设计中算法流程如图 4所示, 在算法设置中, 精英种群不进行选择、交叉、变异等操作, 可以保证进化过程中最优个体不被破坏和丢失。因此将最优个体最少保持代数作为算法终止依据, 这种方式充分利用了遗传算法在进化中的知识积累, 相较于以最大迭代次数作为终止依据更为合理。具体算法参数如表 3所示。

表3

多种群遗传算法参数

3.2 仿真实验

根据上述参数, 进行6次计算求解, 记录数据如表 4所示。

表4

多种群遗传算法仿真实验数据

多种群遗传算法获取的最优解是多个种群协同进化的综合结果, 适应值越小, 说明该序列解对优化目标的满足程度越高。表 4得到的结果显示, 方案4的最优个体适应值最小, 说明该解是当前3个优化目标的最优解。以方案4为例, 其迭代曲线如图 8所示, 该方案的序列解为：

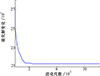thumbnail 图8

多种群遗传算法迭代曲线

由于对舱室没有进行严格限制, 得到的舱室尺寸存在差异, 而在潜艇生活区实际设计中, 其本身舱段内空间紧张, 应尽量提升面积需求大、人员通行较为密集的舱室或区域, 如居住舱室、餐厅等, 根据舱室简化平面将序列解映射到布局中, 根据优化范围对其进行尺寸调整, 得到功能舱室优化布局如图 9所示。

thumbnail 图9

舱室布局优化方案

为了更全面、准确地说明方法的有效性, 本文使用标准遗传算法对仿真案例中的17个舱室重复进行6次计算求解, 算法结束条件保持不变, 个体数量为400, 交叉概率为0.9, 变异概率为0.1。实验结果如表 5所示, 其中方案2结果最优, 将其迭代曲线与图 8的多种群遗传算法优化方案迭代曲线进行对比, 如图 10所示。

表5

标准遗传算法仿真实验数据

thumbnail 图10

算法迭代曲线对比

由仿真实验结果的对比分析得出, 在相同优化目标和参数设定条件下, 本文提出的方法在性能上取得了显著改进。与标准遗传算法相比, 改进多种群遗传算法的平均最优个体适应值优化比约为9.06%, 平均收敛时间优化比约为37.22%, 说明改进多种群遗传算法在优化程度和收敛时间方面均具有明显优势, 更适合应用于舱室布局优化问题的求解。

本文提出的基于多种群遗传算法的舰艇智能仿真布局优化设计方法, 从3个方面考虑布局优化, 在潜艇生活舱室布局中进行验证, 得到的最优解是在满足当前优化目标前提下的较优解。因此, 未来的研究可以在本文基础上展开, 包括但不限于以下三方面:

1) 引入舰艇舱室布局的其他需求, 例如设备布置、人机工效等方面, 完善布局设计;

2) 深入探究舰艇和舱室类型的布局需求差异, 以拓展研究方法的适用范围;

3) 进一步研究人-机协同的设计方法, 在满足智能化、自动化设计的同时, 注重设计人员的参与程度, 以提高设计的质量和完整度。

4 结论

本文从平面简化模型、数学模型以及改进算法等方面分析了潜艇生活舱段的布局优化设计方法的原理和实现。舱室平面简化模型通过建立坐标系, 将优化区域划分为布局行、布局区和待布舱室, 以此建立舱室之间、舱室与梯道、舱室与舱门的节点路径关系。舱室布局数学模型中以邻接强度和流通强度作为表征, 引入模糊处理方法进一步分析舱室间的相对位置关系, 通过定义应急逃生距离增加优化目标, 提高布局的疏散效率。在多种群遗传算法中, 本文结合算法特点, 对各个种群取不同参数, 根据布局优化需求对遗传操作进行了适应性改进, 控制多个种群同时对解空间进行协同搜索。仿真实验显示, 该方法可以在一定程度上保证优化不陷入局部最优解, 具有良好的全局搜索能力, 并且较为快速地完成迭代, 产生优化方案。综上, 本文提出的基于改进多重群遗传算法的多层舰艇智能仿真布局优化设计方法可以为设计人员提供可行的参考方案, 在一定程度上提高舱室布局的自动化和智能化水平。在之后的研究中, 将尝试将该方法应用到舰艇其他舱室, 并对优化目标和算法结构进一步改进和完善, 这将对智能优化舰艇设计产生积极作用。

References

  1. WANG Y L, WU Z P, GUAN G, et al. Research on intelligent design method of ship cabin layout[J]. Marine Technology Society Journal, 2020, 54(2): 79–92. [Article] [Google Scholar]
  2. YE Cong, XU Weizhe, LIU Shuai. Application of ergonomics to layout design of manned submersible[J]. Journal of Northwestern Polytechnical University, 2021, 39(2): 233–240. [Article] (in Chinese) [Google Scholar]
  3. CHEN D, ZHU M, QIAO Y, et al. An ergonomic design method of manned cabin driven by human operation performance[J]. Advanced Design Research, 2023, 1(1): 12–20. [Article] [CrossRef] [Google Scholar]
  4. BURGGRÄF P, ADLON T, HAHN V, et al. Fields of action towards automated facility layout design and optimization in factory planning-a systematic literature review[J]. CIRP Journal of Manufacturing Science and Technology, 2021, 35: 864–871. [Article] [Google Scholar]
  5. WANG Yunlong, WU Zhangpan, LI Kai, et al. Ship cabin intelligent layout design based on tabu search algorithm[J]. Huazhong University of Science and Technology, 2018, 46(6): 49–53 (in Chinese) [Google Scholar]
  6. CAI Wei, CHEN Zhan, CHEN Qi. A new intelligent layout design method for passenger cabins in large cruise ship[J]. Shipbuilding of China, 2019, 60(2): 186–195. [Article] (in Chinese) [Google Scholar]
  7. CAI Wei, CHEN Zhengqiao, HU Min, et al. Intelligent layout of accessible cabin of cruise ships[J]. Ship Engineering, 2022, 44(12): 15–23 (in Chinese) [Google Scholar]
  8. FENG Qing, ZHANG Chengyuan, YU Suihuai, et al. Optimizing residential cabin layout of naval ship with energy method and nsga-Ⅱ algorithm[J]. Mechanical Science and Technology for Aerospace Engineering, 2023, 42(8): 1349–1356 (in Chinese) [Google Scholar]
  9. BAO Meng, HOU Yuanhang, CHEN Wei, et al. Joint optimization of ship cabin passage layout based on genetic algorithm[J]. Journal of Dalian Maritime University, 2021, 47(3): 23–30 (in Chinese) [Google Scholar]
  10. WANG Y L, WU Z P, GUAN G, et al. Research on intelligent design method of ship multi-deck compartment layout based on improved taboo search genetic algorithm[J]. Ocean Engineering, 2021, 225: 108823. [Article] [Google Scholar]
  11. WANG Y, GU Y, ZHANG X, et al. Research on the intelligent layout method of ship multi-deck cabins based on improved SLP and GMBOA[J]. Ocean Engineering, 2024, 295: 116873. [Article] [Google Scholar]
  12. LI H, HOU Y, CHEN W, et al. Optimal design of a ship multitasking cabin layout based on the interval optimization method[J]. Journal of Marine Science and Application, 2021, 20(4): 723–734. [Article]. [Google Scholar]
  13. WANG Z, YANG X Q, ZHENG Y H, et al. Interactive ship cabin layout optimization[J]. Ocean Engineering, 2023, 270: 113647. [Article] [Google Scholar]
  14. LEE K Y, ROH M I, JEONG H S. An improved genetic algorithm for multi-floor facility layout problems having inner structure walls and passages[J]. Computers & Operations Research, 2005, 32(4): 879–899 [Google Scholar]
  15. HU Yao, JIANG Zhifang, XIONG Zhiguo, et al. Warship cabin layout design optimization based on an improved genetic algorithm[J]. Chinese Journal of Ship Research, 2014, 9(1): 20–30. [Article] (in Chinese) [Google Scholar]
  16. LIU Feng, HAN Duanfeng, HAN Haihui. Layout optimization of a huam occupied vehicle manned cabin[J]. Journal of Harbin Engineering University, 2014, 35(1): 30–37 (in Chinese) [Google Scholar]
  17. XUE Liang. Research on the effect of cabin layout of the passenger ship on evacuation ability[D]. Harbin: Harbin Institute of Technology, 2020 (in Chinese) [Google Scholar]
  18. GUO Haiyu, ZHANG Yinghao, LIU Yingming, et al. Optimization design of tuned mass damper for floating wind turbines based on dynamic model and multiple population genetic algorithm[J]. Acta Energiae Solaris Sinica, 2023, 44(11): 217–223 (in Chinese) [Google Scholar]
  19. JERIN LENO I, SARAVANA SANKAR S, VICTOR RAJ M, et al. An elitist strategy genetic algorithm for integrated layout design[J]. The International Journal of Advanced Manufacturing Technology, 2013, 66(9): 1573–1589. [Article] [Google Scholar]
  20. LI Yun, GONG Changqi. Application of improved genetic algorithm in the optimization deign of yacht cabin's layout[J]. Ship & Ocean Engineering, 2010, 39(1): 34–37 (in Chinese) [Google Scholar]
  21. DONG Zengcai, LIU Yindong. Optimization method of ship cabin layout based on reverse learning genetic algorithm[J]. Journal of Dalian Maritime University, 2021, 47(3): 16–22 (in Chinese) [Google Scholar]
  22. KUMAR A, DUTTA K, SRIVASTAVA A. Generating automated layout design using a multi-population genetic algorithm[J]. Journal of Web Engineering, 2023, 22(2): 357–384. [Article] [Google Scholar]
  23. WANG Zhanzhong, ZHAO Liying, CAO Ningbo. Hazardous material transportation scheduling model based on mutilayer coding genetic algorithm[J]. Journal of Jilin University, 2017, 47(3): 751–755 (in Chinese) [Google Scholar]
  24. MINGXIAO S, TIANTIAN L, JUN X. Amphibious vehicle layout optimization based on adaptive elite genetic algorithm[C]//2019 IEEE International Conference on Mechatronics and Automation, 2019: 491–496 [Google Scholar]

All Tables

表1

舱室邻接强度和流通强度等级定义

In the text
表2

舱室信息

In the text
表3

多种群遗传算法参数

In the text
表4

多种群遗传算法仿真实验数据

In the text
表5

标准遗传算法仿真实验数据

In the text

All Figures

thumbnail 图1

生活舱室简化平面布局
In the text
thumbnail 图2

舱室节点路径图
In the text
thumbnail 图3

标准遗传算法流程
In the text
thumbnail 图4

多种群遗传算法流程
In the text
thumbnail 图5

个体编码机制
In the text
thumbnail 图6

染色体基因分组
In the text
thumbnail 图7

2层潜艇生活区初始平面图
In the text
thumbnail 图8

多种群遗传算法迭代曲线
In the text
thumbnail 图9

舱室布局优化方案
In the text
thumbnail 图10

算法迭代曲线对比
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.