Modeling research of group delay ripple on the performance analysis oriented to a satellite direct sequence spread spectrum communication system

Xiongfei LI; Jiqiang ZHAI; Xuemin SUN; Yangming GUO; Guochang ZHOU

doi:10.1051/jnwpu/20254310092

All issues

Volume 43 / No 1 (February 2025)

JNWPU, 43 1 (2025) 92-98

Full HTML

Open Access

Issue		JNWPU Volume 43, Number 1, February 2025


Page(s)		92 - 98
DOI		https://doi.org/10.1051/jnwpu/20254310092
Published online		18 April 2025

JNWPU 2025, 43(1): 92–98

Modeling research of group delay ripple on the performance analysis oriented to a satellite direct sequence spread spectrum communication system

面向卫星直扩通信体制性能分析的群时延波动建模研究

Xiongfei LI (李雄飞)¹^,2, Jiqiang ZHAI (翟继强)², Xuemin SUN (孙学敏)², Yangming GUO (郭阳明)¹ and Guochang ZHOU (周国昌)²

¹ School of Cybersecurity, Northwestern Polytechnical University, Xi'an 710072, China
² China Academy of Space Technology (Xi'an), Xi'an 710100, China

Received: 18 February 2024

Abstract

This study introduces the group delay and its characteristics in satellite channel, meanwhile, the model of the impact of group delay ripple on performance of direct sequence spread spectrum communication system is established and simulated for analysis. The simulation results indicate the specific impact of group delay ripple on system, as well as the impact of group delay ripple on the transmission and reception signals in the spread spectrum communication system. For transmission signals in the spread spectrum system, the group delay ripple can worsen the EVM and Eye-diagram of spread spectrum signal, cause signal distortion and the deterioration of noise tolerance. For the reception performance of the spread spectrum system, the group delay ripple has little effect on the spread spectrum acquisition using incoherent accumulation and energy judgment, but it can cause a deterioration in the error performance of the reception signal. For example, when relative group delay increases from 0.011 to 0.9, the error performance decreases by about 2 dB. When designing satellite spread spectrum communication systems, power resources are extremely precious, it is necessary to consider the impact of group delay on the communication system, and take certain measures to reduce the impact of group delay ripple to the system.

摘要

介绍了卫星信道群时延及其特性, 建立了群时延波动对直接序列扩频通信(简称“直扩通信”)体制性能影响的模型, 仿真分析了群时延波动对扩频通信体制发射和接收信号质量的影响。对于直扩发射信号, 群时延增大会恶化扩频信号EVM和眼图, 使得发射信号产生畸变, 噪声容限恶化。对于直扩接收性能, 群时延的变化对于采用非相干累加和能量判决的扩频捕获基本无影响, 但是会造成接收信号的误码率性能恶化, 相对群时延从0.011增大到0.9时, 误码率性能损失约2 dB。在设计卫星直扩通信系统时, 功率资源极其珍贵, 必须考虑群时延波动对直扩通信系统的影响, 并采取措施, 降低群时延波动对系统的影响。

Key words: group delay ripple / satellite communication / spread spectrum communication system / modeling research

关键字 : 群时延波动 / 卫星通信 / 直扩通信体制 / 建模研究

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

直接序列扩频通信(简称直扩通信)体制因优异的抗干扰性能而广泛应用于卫星通信、导航、测控和物联网中[1–3]。由于扩频后码速率变高, 卫星信道的群时延特性会引起扩频信号失真, 恶化接收误码率, 影响其传输性能。卫星信道的群时延特性基本上由卫星转发器的群时延特性决定[4], 而卫星转发器的群时延特性主要由转发器中的变频电路、滤波电路和放大电路的群时延特性决定。卫星转发器的群时延特性非常复杂, 其中群时延随频率的变化特性称为群时延波动, 如何量化分析群时延波动对卫星直扩通信体制性能的影响是个难点。

卫星直扩通信系统建立在数字通信基础上, 以群时延波动对数字通信的影响为基础，研究其对直扩通信体制性能的影响是可行的。群时延波动对数字相位调制信号影响的研究主要从信噪比损失和误码率恶化2个方面进行: 以最小信噪比损失为准则, 推导出群时延波动对调制信号影响的理论表达式, 并以DPSK信号为例进行分析[5]; 以最小误码率恶化为准则, 仿真出群时延波动对调制信号的影响, 然后拟合出误码率损失曲线, 并以BPSK和QPSK信号为例进行分析[6]。同时, 群时延波动对直扩、跳频等扩频通信系统影响的研究也在推进。文献[7]研究得出了卫星跳频通信系统中时间跟踪对群时延波动较为敏感的结论。文献[8]利用通信系统仿真软件包建立了扩频通信系统在群时延失真信道中的仿真模型, 该模型采用简单的FIR滤波器模拟群时延。文献[9]分析了UWB通信中群时延波动对接收机误码率的影响, 并且采用蒙特卡洛方法进行仿真验证。文献[10]分析了群时延波动对微波光子相位调制滤波器的影响。近年来, 随着宽带扩跳混合扩频体制在卫星转发器中的应用, 人们开始研究群时延波动对混合扩频通信系统的影响。文献[11]研究了群时延波动对宽带直扩跳频通信系统解调门限的影响, 文献[12]研究了群时延波动对混合扩频信号应用于卫星测量系统的影响。上述研究均表明卫星转发器中采用直扩、跳频通信体制不能忽略群时延波动的影响, 必须采取合适的群时延自适应补偿算法或测量后进行补偿的方法降低群时延波动的影响, 保障系统正常工作[13–15]。

上述研究均以群时延特性对扩频通信系统发射机或者接收机某一方面的影响因素如误码率进行研究, 未从卫星直扩通信系统全貌进行建模研究, 具有一定的局限性。此外, 随着卫星载荷集成度大幅提高[16], 转发器前后端群时延波动呈变大趋势, 对直扩通信体制性能影响已经非常明显。因此, 面向卫星通信应用, 全面系统地建模研究群时延波动对卫星直扩通信体制的影响具有重要意义。本文首先介绍卫星信道群时延及其特性; 其次建立群时延波动模型，分析对直扩发射和接收性能的影响，最后进行仿真分析。

1 卫星信道群时延及其特性分析

卫星信道的群时延主要由卫星转发器群时延决定, 以透明卫星转发器为例, 转发器的群时延特性主要由输入复用器(input multiplexer, IMUX)和输出复用器(output multiplexer, OMUX)决定, 忽略对群时延特性影响较小的因素, 则对转发器群时延的研究可采用如图 1所示的简化模型，如(1)式所示。

图1

卫星转发器简化模型

在卫星直扩通信系统中, 直扩码速率越高, 传输所占带宽越宽, 群时延的影响越大。对卫星信道的相频特性ϕ(ω)用幂级数来逼近

式中，ω_c为系统带宽的中心频率。则信道的群时延特性可以表示为

式中，第2项是(ω-ω_c)的线性函数, 代表线性失真; 第3项与(ω-ω_c)²呈正比, 称为抛物线失真。

因此, 卫星直扩通信中信道的群时延主要是第2项线性群时延和第3项抛物线群时延, 如图 2所示。其中f_c为载波频率, 带宽B=2f_s, 最大群时延失真为d。这个群时延失真随频率的变化特性被称为群时延波动。群时延波动情况较复杂, 一个合理的假设是群时延围绕一个期望值波动[17]。

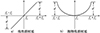图2

线性群时延与抛物线群时延

相同的群时延在不同的扩频码速率下对信号的失真是不同的, 群时延相同时, 扩频码速率越高, 信号的失真越大。因此, 可以用最大群时延d和信道传输的扩频码速率R_c的乘积作为群时延失真的指标，如(3)式所示。

考察信道群时延波动对系统性能的影响时, 一般假定信道不存在幅度失真, 则信道等价为全通网络, 其传输函数为

这样的全通滤波器是一个线性时不变(linear time-invariant, LTI)系统, 满足带通等价定理, 因此任何频段的群时延波动对系统的影响都等效于相同的基带群时延波动对系统的影响[17]。

除了经常利用线性模型和抛物线模型进行研究外, 对于某个特定的卫星通信系统, 可以先利用群时延测量技术测得系统的真实群时延波动特性, 或者对系统真实群时延波动进行预判分析[18], 然后通过设计专用的滤波器进行模拟。

2 面向卫星直扩通信体制性能分析的群时延波动建模

卫星直扩通信收发模型如图 3所示, 具体描述如下: 在直扩发射机中, 扩频码序列c(t)与待传信息a(t)相乘, 得到直扩信号d(t), 直扩信号d(t)经射频载波f_c调制后得到直扩发射信号s(t)。在直扩接收机中, 本地载波f_c0和通过卫星信道的射频接收信号混频滤波后得到r(t), 然后用与发射机中同步的本地扩频码序列与r(t)进行相关运算, 实现解扩得到r_cor(t), 经解调后恢复出原始信息a′(t)。

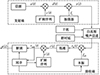图3

直扩通信信号收发模型

设a(t)的码元间隔为T_a, a(t)表达式为

式中: 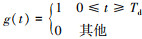, 表示设定的门限函数, a_n表示输入的原始信息。

伪随机序列c(t)的码片宽度为T_c, 其表达式为

直扩的运算过程其实是将序列a(t)与扩频码c(t)做异或运算, 从而产生扩频后序列d(t), 即

式中, 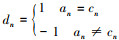。对d(t)进行载波调制, 处理后得到发送信号，即

式中：f_c为载波频率; θ₀为载波初相。

直扩发送信号s(t)经过信道后, 考虑抛物线群时延影响, 群时延为τ(f), 经过复数下变频后的接收信号为

式中: τ为频点f_c0处的群时延; θ为收发相位误差; θ₀为初始相位。

经过低通滤波后运算得到信号

式中，f_e为残余频差。

r(t)与本地扩频码进行相关运算得到接收的信息

对r_rec(t)进行解调即可得到解调信息a′(t)。

假设直扩发射信号经过理想信道, 通道不存在群时延波动, 则可以得到参考信号r_c(t)。

对接收到信号的误差矢量幅度(error vector magnitude, EVM)计算如下

式中：I_k表示参考信号r_c(t)第k个符号的同相分量；Q_k表示参考信号r_c(t)第k个符号的正交分量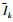表示接收到信号r_rec(t)第k个符号的同相分量;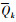表示接收到信号r_rec(t)第k个符号的正交分量, N表示输入信号的长度; E_RMS表示计算的平均EVM, 其中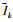和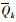中已包含群时延为τ(f)。

3 面向卫星直扩通信体制性能分析的群时延波动仿真

由于群时延波动对直扩通信体制性能影响的理论推导极其复杂, 采取仿真方法进行分析。以某卫星通信系统为例, 采用直扩体制, Ka频段, 通道链路群时延1~10 ns, 带宽增大, 群时延会增大, 符号速率20 kb/s, 扩频后chip速率为10 Mb/s, 带宽为20 MHz, 接收端信噪比E_b/N₀为5 dB。因此, 仿真选取20 MHz带宽内的抛物线群时延波动特性, 具体分析参数选取如表 1所示。

表1

仿真分析参数

3.1 群时延波动对卫星直扩体制发射信号质量的影响

卫星发射信号质量一般用误差矢量幅度和眼图衡量。在上述仿真参数下, 扩频后归一化群时延相对于扩频前归一化群时延增大了500倍, 即扩频倍数(也叫扩频因子)为500。计算不同群时延波动下的EVM, 如图 4所示。可以看出随着群时延波动的增大, 扩频信号EVM急剧恶化, 群时延从1.1 ns增大到90 ns, EVM从0.1%恶化到46%。EVM的恶化反映信号发送质量变差, 影响信号的接收性能, 一般中频信号(频点约200 MHz)EVM小于2%左右对信号接收性能无影响。EVM过大会影响接收性能。

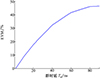图4

不同群时延下的EVM计算

对不同群时延波动下眼图进行仿真，结果如图 5所示。从眼图中可以看出，随着群时延波动的变大, 扩频信号眼图形状发生变化, 信号畸变越来越严重, 噪声容限恶化, 最终会影响接收的误码率性能。

图5

不同群时延下的眼图变化

3.2 群时延波动对卫星直扩体制接收性能的影响

卫星直扩信号的接收主要包括捕获和跟踪两部分, 一般用捕获概率衡量捕获性能, 用误码率衡量跟踪性能。在卫星通信系统中, 特别是对于星间通信系统, 发送方的功率大小直接影响接收方的性能, 一般发送功率越大, 信噪比越高, 接收性能越好, 但是增大发送功率会增加发送方的质量、成本及技术难度, 因此在满足使用要求的情况下, 应尽可能降低发送方发送功率。根据卫星通信实际工作场景, 在通信距离、通信频段、通信速率、收发天线大小一定的情况下, 发送方发送的功率决定了接收方的信噪比大小, 因此可以通过仿真不同群时延波动在不同信噪比下的性能，反映群时延对实际卫星通信性能的影响。下面主要从扩频信号捕获概率和误码率2个方面进行仿真分析, 得出不同信噪比、不同群时延波动对扩频信号捕获和跟踪性能的影响。

采用蒙特卡洛方法, 仿真1 000次取平均。在无群时延条件下, E_b/N₀为5 dB时, 通过非相干累加, 捕获概率能够达到98%。在相同信噪比条件和捕获处理方式下, 加入不同的群时延波动, 捕获概率仿真曲线如图 6所示。可以看出, 相同的信噪比下, 不同群时延波动对捕获概率影响较小, 因为直扩信号的捕获主要是利用单个符号相干积分后, 对多个符号进行非相干累加, 得到能量后进行门限判决, 群时延波动对非相干累加后的符号能量影响较小, 因此对捕获概率影响较小。

图6

不同群时延波动、E_b/N₀下捕获概率

图 7为不同群时延波动、E_b/N₀下的误码率仿真结果, 仿真比特个数为100 000。从图 7中可以看出, 相同E_b/N₀下, 随着群时延波动的增大, 误码性能下降, 相对群时延波动从0.011增大到0.9(绝对群时延从1.1 ns增大到90 ns), 群时延波动对误码性能的影响呈增大趋势。相对群时延波动为0.6时, 误码性能下降约1 dB, 相对群时延波动为0.9时, 误码性能下降约2 dB。因此, 若不采取降低群时延波动影响的方法, 为了得到同样的误码率性能, 通信系统需要对于不同的群时延波动增大相应的发送功率, 这就增大了系统的开销。

图7

不同群时延波动、E_b/N₀下误码率

图 8为不同扩频因子、E_b/N₀下误码率仿真结果。从图 8中可以看出, 在同一个相对群时延波动下(图中仿真相对群时延为0.6), 不同扩频因子(扩频因子16, 128, 500)下误码性能没有变化, 改变扩频比不能减小群时延波动对扩频系统造成的影响。

图8

不同扩频因子、E_b/N₀下误码率

4 结论

群时延波动会带来数字通信系统的信噪比损失和误码率恶化, 特别是对于卫星直扩通信体制, 扩频后的归一化群时延会增大相应倍数。仿真分析了群时延波动对直扩通信系统发射信号和接收信号的影响, 对于直扩发射信号, 群时延波动的增大会使得信号EVM和眼图形状发生变化, 信号畸变越来越严重, 噪声容限恶化。对于直扩接收性能, 群时延波动对于采用非相干累加和能量判决的直扩信号捕获基本无影响, 但是会造成接收信号的误码率性能的恶化, 相对群时延从0.011增大到0.9时, 误码率性能恶化最大约2 dB。因此在设计卫星直扩通信系统时, 由于功率资源极其珍贵, 必须考虑群时延波动对体制的影响, 并通过采取自适应均衡、群时延波动预判和群时延波动测量后补偿等技术措施, 降低群时延波动对直扩通信体制的影响, 保证直扩通信体制在卫星通信转发器中的性能。

References

GUO XiaoxuXU ZhaobinCHENG Hengfei, et al. High sensitivity fast acquisition algorithm for inter-satellite communication[J]. Journal of Harbin Institute of Technology, 2023, 55(8): 43–50 (in Chinese) [Google Scholar]
LUO JinXIA JiabaoBAI Yang, et al. Interleaved-LoRa transmission scheme for satellite IoT[J]. Space Integrated Ground Information Networks, 2023, 4(1): 89–97 (in Chinese) [Google Scholar]
SUN ZhiguoMAO HuiminWANG Zhenduo, et al. Self-interference suppression of a self-encoded spread spectrum system based on period interpolation[J]. Journal of Harbin Engineering University, 2023, 44(3): 489–495 (in Chinese) [Google Scholar]
HOU LimingSUN BaoshengLU Xiaoming. Impact of group delay on BER performance in high data rate satellite relay systems[J]. Journal of Spacecraft TT & C Technology, 2006, 25(2): 54–58 (in Chinese) [Google Scholar]
LIU XMOLLENAUER L FWEI X. Impact of group-delay ripple in transmission systems including phase-modulated formats[J]. IEEE Photonics Technology Letters, 2004, 16(1): 305–307 [Article] [Google Scholar]
AZIZZADEH A, MOHAMMADI L. Degradation of BER by group delay in digital phase modulation[C]//Fourth Advanced International Conference on Telecommunications, Athens, Greece, 2008: 350–354 [Google Scholar]
LIST N B. Effect of group delay variation on time tracking for frequency hopped satellite systems[C]//Military Communications Conference, Washington, DC, USA, 2006: 1–6 [Google Scholar]
CHEN HuiYI KechuLI Wenduo. Simulation and analysis of the influence of group delay on the performance of a spread spectrum communication system[J]. Telecommunication Engineering, 2006, 46(2): 111–113 (in Chinese) [Google Scholar]
JIN Y, KWAK K S. The impact of group delay ripple for TR UWB communication system[C]//The 11th International Symposium on Communications & Information Technologies, Hangzhou, China, 2011: 417–421 [Google Scholar]
MOKHTARI A, AKBARI M. The group delay ripple effects on the performance of phase-modulator based microwave-photonic filter[C]//The 18th International Conference on Telecommunications, Ayia Napa, Cyprus, 2011 [Google Scholar]
TIAN YuWAN XiaoguangJIN Ye, et al. Analysis of group-delay distortion effect on wide-band DS/FH satellite communication system[J]. Aerospace Shanghai, 2015, 32(5): 38–53 (in Chinese) [Google Scholar]
ZHANG ZongpanWANG NanLIU Ruizhu. Analysis of the influence of group delay on hybrid spread-spectrum reception[J]. Electronic Science and Technology, 2018, 31(4): 73–76 (in Chinese) [Google Scholar]
YANG ZhixingDENG YongjunPAN Changyong, et al. Analysis of the influence of group delay on hybrid spread-spectrum reception[J]. Journal on Communications, 2006, 27(8): 88–92 (in Chinese) [Google Scholar]
XIAO Zhibin, LIU Yingxiang, TANG Xiaomei, et al. Group delay measurement method based on narrow-band spread spectrum signals[J]. Electronics Letters, 2014, 50(5): 372–374 [Article] [Google Scholar]
WANG YifengXIAO ZhibinLI Pengpeng, et al. Receiver group delay measurement technology based on carrier phase[J]. Systems Engineering and Electronics, 2022, 44(4): 1078–1084 (in Chinese) [Google Scholar]
LIU YueHUANG YinLIN Yujie, et al. Recent advances of phased array application in satellite-terrestrial convergence networks[J]. Space Electronic Technology, 2023, 20(6): 52–63 (in Chinese) [Google Scholar]
TAN XiaohengLI YushuanLI Tengjiao. Simulation and analysis of influence of group delay distortion on performance of QPSK communication system[J]. Journal of System Simulation, 2008, 20(21): 5976–5978 (in Chinese) [Google Scholar]
LI BinSU JiaqiCHEN Guowei, et al. Prejudgment and analysis of the distortion of group delay ripple for high-sensitivity automatic gain control receiver[J]. Acta Electronica Sinica, 2023, 51(8): 2011–2019 (in Chinese) [Google Scholar]

All Tables

表1

仿真分析参数

In the text

All Figures

	图1 卫星转发器简化模型
In the text

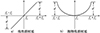	图2 线性群时延与抛物线群时延
In the text

	图3 直扩通信信号收发模型
In the text

	图4 不同群时延下的EVM计算
In the text

	图5 不同群时延下的眼图变化
In the text

	图6 不同群时延波动、E_b/N₀下捕获概率
In the text

	图7 不同群时延波动、E_b/N₀下误码率
In the text

	图8 不同扩频因子、E_b/N₀下误码率
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] GUO XiaoxuXU ZhaobinCHENG Hengfei, et al. High sensitivity fast acquisition algorithm for inter-satellite communication[J]. Journal of Harbin Institute of Technology, 2023, 55(8): 43–50 (in Chinese) [Google Scholar]

[2] LUO JinXIA JiabaoBAI Yang, et al. Interleaved-LoRa transmission scheme for satellite IoT[J]. Space Integrated Ground Information Networks, 2023, 4(1): 89–97 (in Chinese) [Google Scholar]

[3] SUN ZhiguoMAO HuiminWANG Zhenduo, et al. Self-interference suppression of a self-encoded spread spectrum system based on period interpolation[J]. Journal of Harbin Engineering University, 2023, 44(3): 489–495 (in Chinese) [Google Scholar]

[4] HOU LimingSUN BaoshengLU Xiaoming. Impact of group delay on BER performance in high data rate satellite relay systems[J]. Journal of Spacecraft TT & C Technology, 2006, 25(2): 54–58 (in Chinese) [Google Scholar]

[5] LIU XMOLLENAUER L FWEI X. Impact of group-delay ripple in transmission systems including phase-modulated formats[J]. IEEE Photonics Technology Letters, 2004, 16(1): 305–307 [Article] [Google Scholar]

[6] AZIZZADEH A, MOHAMMADI L. Degradation of BER by group delay in digital phase modulation[C]//Fourth Advanced International Conference on Telecommunications, Athens, Greece, 2008: 350–354 [Google Scholar]

[7] LIST N B. Effect of group delay variation on time tracking for frequency hopped satellite systems[C]//Military Communications Conference, Washington, DC, USA, 2006: 1–6 [Google Scholar]

[8] CHEN HuiYI KechuLI Wenduo. Simulation and analysis of the influence of group delay on the performance of a spread spectrum communication system[J]. Telecommunication Engineering, 2006, 46(2): 111–113 (in Chinese) [Google Scholar]

[9] JIN Y, KWAK K S. The impact of group delay ripple for TR UWB communication system[C]//The 11th International Symposium on Communications & Information Technologies, Hangzhou, China, 2011: 417–421 [Google Scholar]

[10] MOKHTARI A, AKBARI M. The group delay ripple effects on the performance of phase-modulator based microwave-photonic filter[C]//The 18th International Conference on Telecommunications, Ayia Napa, Cyprus, 2011 [Google Scholar]

[11] TIAN YuWAN XiaoguangJIN Ye, et al. Analysis of group-delay distortion effect on wide-band DS/FH satellite communication system[J]. Aerospace Shanghai, 2015, 32(5): 38–53 (in Chinese) [Google Scholar]

[12] ZHANG ZongpanWANG NanLIU Ruizhu. Analysis of the influence of group delay on hybrid spread-spectrum reception[J]. Electronic Science and Technology, 2018, 31(4): 73–76 (in Chinese) [Google Scholar]

[13] YANG ZhixingDENG YongjunPAN Changyong, et al. Analysis of the influence of group delay on hybrid spread-spectrum reception[J]. Journal on Communications, 2006, 27(8): 88–92 (in Chinese) [Google Scholar]

[14] XIAO Zhibin, LIU Yingxiang, TANG Xiaomei, et al. Group delay measurement method based on narrow-band spread spectrum signals[J]. Electronics Letters, 2014, 50(5): 372–374 [Article] [Google Scholar]

[15] WANG YifengXIAO ZhibinLI Pengpeng, et al. Receiver group delay measurement technology based on carrier phase[J]. Systems Engineering and Electronics, 2022, 44(4): 1078–1084 (in Chinese) [Google Scholar]

[16] LIU YueHUANG YinLIN Yujie, et al. Recent advances of phased array application in satellite-terrestrial convergence networks[J]. Space Electronic Technology, 2023, 20(6): 52–63 (in Chinese) [Google Scholar]

[17] TAN XiaohengLI YushuanLI Tengjiao. Simulation and analysis of influence of group delay distortion on performance of QPSK communication system[J]. Journal of System Simulation, 2008, 20(21): 5976–5978 (in Chinese) [Google Scholar]

[18] LI BinSU JiaqiCHEN Guowei, et al. Prejudgment and analysis of the distortion of group delay ripple for high-sensitivity automatic gain control receiver[J]. Acta Electronica Sinica, 2023, 51(8): 2011–2019 (in Chinese) [Google Scholar]