EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 2 (April 2025) JNWPU, 43 2 (2025) 212-221 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 2, April 2025
Page(s) 212 - 221
DOI https://doi.org/10.1051/jnwpu/20254320212
Published online 04 June 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

地月空间存在着丰富的太空资源，已成为世界各大国竞相角逐的新疆域。未来对地月空间的大规模探索与开发，航班化运输网络成为常态化地月往返的必然需求[1–2]。因而，建立经济可持续的运输体系成为关键问题。与地球表面相比，地月平动点具有引力势能高的优势，从其出发完成各类空间任务更节省燃料[1, 3]，这使得地月空间平动点轨道成为深空探测任务的重要枢纽。美国正在推进实施的“门户”地月空间站任务就计划将空间站部署于月球附近的近直线晕轨道上，作为月球探测及未来火星探测的中转站[4]。因此，基于平动点中转站的低能转移轨道设计研究受到广泛关注。

平动点轨道主要包括周期轨道和拟周期轨道。目前许多基于平动点轨道的转移轨道设计研究基于周期轨道展开，但对于某些周期轨道而言，其形状细长，不利于航天器通信链路的构建[5]。而拟周期Lissajous轨道可独立选取水平和垂直幅值，具有更多的形状和选择，更具任务的灵活性，适合航天任务的需求[6–7]。此外，Lissajous轨道的维持成本同样较低[8]，适合作为未来地月空间航班化运输的中转站轨道。而目前针对Lissajous中转站的低能转移轨道特性尚不明确，借力方位角、借力高度和中转站轨道入轨点位置等如何选取成为值得研究的问题。本文基于地月系统L2点Lissajous中转站展开研究。

基于中转站的直接转移是地月空间航班化运输中最为传统、消耗最高的一种形式，但转移时间短、技术较为成熟的优势使其未来更多服务于对任务安全性有严格要求的载人运输。而对于大规模载物运输，需要更为经济的转移方式。小推力技术具有节省燃料的优势，被认为具有广阔的应用前景。Du等[9–10]研究了地球同步轨道到平动点轨道、平动点轨道之间等的小推力转移。但小推力转移中的多圈环绕轨迹需要连续的轨道控制且会造成转移时间过长，不适合于一般的航班化运输任务。目前，脉冲式地月低能转移轨道主要基于弱稳定边界(weak stability boundary, WSB)理论和不变流形理论进行构建[11]。WSB本质是利用太阳引力，降低被月球捕获的速度，但转移时间过长，以地月转移为例，一般需要80~120 d的转移时间[12]，限制了其应用性。而结合不变流形理论构建的转移轨道，虽然转移脉冲与WSB方式相比增加至少100 m/s，但转移时间只需6~30 d左右[13]，适用于载物运输。

基于不变流形理论，众多学者对低能转移轨道设计展开了丰富的研究。Rausch[14]结合不变流形理论和微分修正技术实现了从地球停泊轨道至地月L1点和L2点halo轨道的双脉冲转移轨道设计，并在星历模型下进行了重现。在同样场景下，Parker和Born[15]采用双脉冲转移与自然流形拼接的方式构造了转移轨道，进一步降低了转移脉冲，并针对转移时间短和长2种情况下的转移轨道特性展开了研究。采用同样的设计方法，Alessi等[16]研究了从近地轨道(low earth orbit, LEO)至地月L1点和L2点Lissajous轨道的转移轨迹。采用单脉冲转移，Santos等[17]建立了应用自然稳定流形实现从月球停泊轨道至地月L2点halo轨道的优化问题，并采用非线性规划方法进行求解，得到了最小化Δv的低能转移轨道。结合地球至平动点轨道和平动点轨道至月球的设计研究，Zheng等[18]提出了一种基于不变流形和混沌控制的混合法来设计地球停泊轨道至月球轨道的低能转移，将轨道分为2段进行设计，并通过庞加莱截面进行拼接。近年来，随着航天任务需求的多样化，不变流形理论应用于不同场景和结合不同推力技术的研究相继开展，例如：在“门户”空间站背景下利用NRHO的不变流形进行航天器交会前的调相轨道设计[19–20]、考虑月球基地的建设利用不稳定流形实现平动点轨道至月表的低能量转移[21–22]、结合小推力与不变流形的转移轨道优化设计等[23–24]。

为了进一步降低消耗，Gordon[25]将自然不变流形和月球引力辅助(lunar gravity assist, LGA)相结合，构造了地月系统L2点halo轨道的双脉冲转移。然而，Gordon的研究工作中未涉及到L1点附近的轨道，且所应用的自然流形形式局限性较大。在此基础上，李明涛[13]提出了三脉冲转移方法，通过在halo轨道处施加一入轨脉冲获得摄动流形代替自然稳定流形，不仅缩短了转移时间，还提升了月球借力效果。为了探索影响月球借力效果的因素，曾豪等[26–27]对halo轨道等周期轨道的月球借力高度、借力方位和入轨点位置进行了进一步分析。然而，文献[13, 26]中采用的脉冲入轨策略对自然流形距离月球较远的入轨点而言无法充分发挥减小燃料消耗的优势，尤其对于大幅值平动点轨道。且采用的微分修正法依赖于初值的选择，无法保证求解结果为全局最优。此外，目前基于Lissajous中转站轨道的低能转移轨道特性尚不明确，借力高度、轨道入轨点、轨道幅值等设计参数对转移轨道特性有何影响有待揭示。

针对以上问题，本文提出了一种改进的三脉冲转移设计方法，并通过优化求解燃料最优转移轨道。采用自然流形与摄动流形拼接的形式代替传统的脉冲入轨策略，既能降低消耗，增加有效入轨点的选择范围，又能提升方法对于大幅值Lissajous中转站轨道的适用性。采用粒子群算法(particle swarm optimization, PSO)和序列二次规划(sequential quadratic programming, SQP)算法对整条转移轨道进行分段优化求解，避免了采用数值方法对初值的严重依赖。选取L2点Lissajous中转站轨道为研究对象，重点分析了月球借力方位角、借力高度、轨道入轨点位置、Lissajous轨道幅值和星历模型下其他天体引力对转移轨道的消耗和时间特性的影响，为未来地月空间航班化运输网络的构建提供参考。

1 动力学模型

1.1 圆型限制性三体模型

本文基于圆型限制性三体模型(CRTBP)研究地月系统转移轨道设计问题。在CRTBP中，航天器的运动在质心旋转坐标系中描述，如图 1所示。其中，原点位于地月系统的质心，x轴方向由地球指向月球，z轴方向与月球绕地球的旋转方向一致。为了便于研究，采用了无量纲化处理简化模型，具体的细节可查阅文献[28]。最后，可得到航天器的动力学方程为

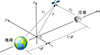thumbnail 图1

圆型限制性三体模型示意图

式中

式中: Ω3表示系统的有效势; μ为质量参数, 在地月系统中, 其值为0.012 15;r1和r2分别为航天器到地球和月球的距离。

1.2 星历模型

CRTBP模型假设月球绕地球的相对运动为圆周运动, 是三体问题的简化模型。此外, 模型建立中未考虑太阳等第三体引力摄动对真实轨道有着不可忽略的影响[29]。因此, 为了保证设计结果的可靠性, 需要将CRTBP中设计的轨道转换到高精度的星历模型中进行修正。以i表示中心天体, j表示航天器, k表示其他摄动天体, N体星历模型方程为

式中: 带2个下标的向量r表示对应2个物体的位置向量, 方向由后者指向前者, 如rkj表示航天器相对于第k个摄动天体的位置; 中心天体和其他摄动天体的实时状态可通过JPL的DE430星历获得。

1.3 Lissajous轨道及其不变流形

Lissajous轨道是存在于共线平动点附近的一类拟周期轨道。这类轨道可以分解为两主天体运动平面内的周期运动与平面外周期运动的合成, 因此可以独立选择面内和面外幅值。

Lissajous轨道的求解方法主要可以分为2类: 解析方法和数值方法。解析方法主要利用Lindstedt-Poincar (L-P)方法获得高阶解析解[30–32], 但该方法的推导过程较为繁琐。本文采用基于多重打靶法[33]的数值方法进行求解, 需利用Lissajous轨道的低阶解析解[31]作为初值。

选取初始振幅Ay=15 000 km, Az=15 000 km, 初始振动相位θxy=π, θz=π/2, 图 2为CRTBP模型下的Lissajous轨道及其内部不变流形, 本文主要利用了其内部稳定流形。图中距离单位1 LU为384 400 km。

thumbnail 图2

Lissajous轨道及其内部不变流形

2 转移轨道设计与优化

2.1 转移方案

结合月球引力辅助与不变流形, 本节将采用三脉冲转移方式设计LEO至L2点Lissajous中转站的低能转移轨道。具体地, 第1次脉冲施加于LEO处, 使航天器进入地月直接转移段并飞越月球; 第2次脉冲施加于近月点处, 增强月球借力效果并使航天器进入摄动流形段; 第3次脉冲施加于摄动流形与自然流形的拼接点处, 使航天器进入自然流形段并最终被目标轨道捕获, 过程示意图如图 3所示。

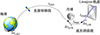thumbnail 图3

转移轨道示意图

由于三体模型下动力学环境复杂, 轨道对初值极为敏感, 对于上述三脉冲转移轨道燃料最优优化问题, 优化变量较多, 直接求解难度较大。因此, 本节采用分段优化方法, 降低求解问题的难度。具体地, 与文献[26, 34]中的方法类似, 将整条转移轨道分为2段, 包括从LEO到月球飞越的直接转移段和从月球飞越到Lissajous轨道的流形拼接段, 示意图如图 3所示。

为了便于利用Lissajous轨道的自然稳定流形进一步降低转移脉冲, 本节将采用逆向设计。将Lissajous轨道按等时间间隔离散, 以1个主周期均分为360个入轨点为例, 其示意图如图 4所示。

thumbnail 图4

Lissajous轨道离散示意图

2.2 LGA至Lissajous流形拼接段

从图 2b)中可以看出, Lissajous轨道的自然稳定流形虽能接近月球但仍存在一定距离, 且未能满足月球借力的一些条件。文献[26, 34–35]中在平动点轨道入轨处施加一脉冲修正自然稳定流形以满足一定的月球借力条件, 但对于一些平动点轨道入轨点而言, 该种方法所需的修正脉冲较大, 在一定程度上减小了借助不变流形节省消耗的优势。这种现象对于大幅值平动点轨道中距离月球较远的自然稳定流形而言更为明显。事实上, 摄动流形段的最佳脉冲施加点并不一定在平动点轨道附近, 下面通过仿真进一步说明。设置L2点Lissajous中转站轨道初始幅值为Ay=15 000 km, Az=15 000 km, 将时间为[0, 2π]内的轨道等时间间隔离散为360个点, 选取若干入轨点对该现象进行示例说明, 约束条件设置为月球借力高度为100 km，借力方位类倾角为10°。结果如图 5所示。

thumbnail 图5

流形拼接段转移脉冲、转移时间与自然流形时长曲线

图 5中横坐标表示自然流形段时长占所允许的总自然流形时长的比例, 图中的各标记点表示各入轨点流形拼接脉冲最小时的位置和对应的转移时间。从图 5a)中可以看出, 选取的Lissajous中转站轨道的入轨点为第1, 5和10点时, 自然流形和摄动流形拼接的形式均在一定程度上减少了转移脉冲, 且从图 5b)中可以看出转移时间会更短。其中, 与文献[26, 34–35]中采用的脉冲入轨方式相比，入轨点为第1和第5点时最优转移脉冲降低了约400 m/s, 入轨点为第10点时降低了约18 m/s。高能耗入轨点第1点和第5点在以往的研究中通常不会被选取, 而通过流形拼接降低转移脉冲的形式则增加了入轨点的有效选取范围。当然, 这并不意味着以往研究中不可取的所有入轨点通过该种方法均能转换为可取, 也不能说明在所有入轨点情况下采用流形拼接形式所需的转移脉冲均能降低。

为了更进一步降低LGA至Lissajous中转站的脉冲消耗, 本节在设计与求解优化问题中考虑流形拼接的形式。此时, 优化变量总结为

式中: tNSM表示自然稳定流形段的时间; tPM表示摄动流形段的时间; ΔvLMI表示摄动流形与自然流形拼接点处的脉冲。

构造全局优化问题描述如下

式中: J(x1)表示目标函数; 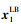和 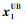分别表示优化变量的下界和上界; ci(x1)=qi(i=1, 2, …, m1)和ci(x1)≥qi(i=m2, …, m)分别为等式约束和不等式约束。

通过放松约束, 本节将采用PSO算法对上述优化问题进行初步求解。继续以PSO优化结果为初值采用SQP算法进一步寻优, 获得严格满足约束条件的最优解。在CRTBP模型下, 采用双层优化方法求解LGA至Lissajous流形拼接段的非线性等式约束包括借力高度、借力方位角和航迹角, 优化变量取值范围如表 1所示。此外, 为防止转移轨迹与月球碰撞, 还需考虑非线性约束

表1

流形拼接段优化变量的取值范围

2.3 LEO至LGA直接转移段

对于LEO至LGA直接转移段, 采用与2.2节相同的双层优化方法进行求解。此时, 优化变量为

式中: Δ vLFB表示在月球飞越处施加的脉冲; tDTS表示直接转移段的时间。

值得注意的是, 该段的优化目标中并没有包含从LEO逃逸的脉冲ΔvLEO, 这是因为在本文的研究中并未考虑LEO的倾角约束。在此情况下, LEO逃逸脉冲ΔvLEO大小为3.1 km/s左右, 对优化结果无明显影响。具体地, 优化变量的参数范围如表 2所示。

表2

直接转移段优化变量的取值范围

2.4 初值获取

一般而言, 优化算法不依赖于初值的选取, 但在本文的轨道优化问题中, 由于三体模型下轨道对初值的敏感性和优化问题本身的强约束性, 给定优化变量参数范围随机生成初始种群后，直接优化会导致优化过程难以进行下去, 且难以满足非线性约束。因此, 本节采用数值方法先获取满足一定约束条件的结果作为优化的初值。

对于LGA至Lissajous流形拼接段, 可以利用自然不变流形为初值, 采用微分修正法可快速获取满足约束条件的轨道。而对于LEO至LGA直接转移段, 本节采用Lambert转移和多重打靶法[36]获取满足连续性条件的轨道。

3 转移特性分析

3.1 借力方位对借力效果的影响

从仿真结果中发现, 借力方位对月球借力效果有着不可忽略的影响, 该结论在文献[26]中得到印证。但如何选取最优借力点方位, 文献[26]中并未做更详细说明。本节进一步研究了借力方位变化对借力效果的影响。在数值验证中发现, 借力方位中类倾角比类升交点赤经对借力效果的影响更大, 且在[-30°, 30°]之间影响更明显。其中, 类倾角和类升交点赤经在旋转坐标系下定义, 其求解和月心惯性系下环月轨道倾角与升交点赤经相似[27]。因此, 本节仅针对变化范围在[-30°, 30°]之间的借力方位类倾角做更进一步研究。选择Lissajous中转站轨道初始幅值为Ay=15 000 km, Az=15 000 km, 设置LEO出发高度为167 km, 借力高度为100 km, 得到转移脉冲Δv和转移时间T随借力方位类倾角的变化情况如图 6所示。

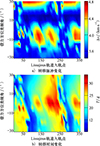thumbnail 图6

不同入轨点和类倾角的转移脉冲与转移时间变化图

从图 6中可以看出, 借力方位类倾角对转移脉冲的影响非常明显。总体而言, 在15°左右, 转移脉冲均较小, 在3.45 km/s左右, 但转移时间绝大部分处于15~25 d之间。因此, 在优化过程中考虑类倾角对于获取最优转移轨道是非常有必要的。在后续优化过程中, 类倾角约束以-30°∶5°∶30°的离散形式给出。

3.2 借力高度和轨道入轨点的影响

选择Lissajous中转站轨道初始参数与3.1节一致, 考虑不同的借力高度非线性约束, 采用第2节所描述的双层优化方法进行优化求解, 得到不同入轨点的转移脉冲和时间变化能图如图 7所示。

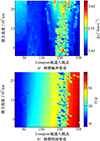thumbnail 图7

不同入轨点和借力高度的转移脉冲与时间的变化能图

从图 7中可以看出, 不同借力点高度和轨道入轨点下的转移脉冲在3.43~3.68 km/s之间, 与直接转移相比[13], 转移脉冲节省了200~600 m/s。但对应的转移时间在8~38 d之间, 比直接转移时间更长。因而, 考虑到载人任务的安全性, 这种转移方式更适合于载物运输任务。

此外, 从图 7a)中可以看出, 从LEO转移至Lissajous轨道入轨点为第1~225点的所需转移脉冲都较小, 在3.43~3.53 km/s之间。且从能图的颜色变化来看, 对大部分入轨点而言, 随着借力点高度增加, 借力效果下降。但相应入轨点的转移时间特性却有不一样的规律, 从图 7b)中可以看出, Lissajous轨道入轨点为第1~65点的转移时间不超过15 d, 且随借力点高度增加, 转移时间虽有所增加但不明显; 入轨点为第66~140点和第141~200点的转移时间分别在15~20 d和20~25 d之间, 且均基本不受借力点高度变化影响。结合图 7a)~7b)可以看出, 入轨点第225~300点附近呈现“混沌”现象, 转移轨道对参数高度敏感, 在该区域执行任务存在不确定性, 因而不适用于实际任务中。然而, 入轨点第225~300点“混沌”区域和入轨点第301~360点区域具有相似转移特性。即对于入轨点为第225~360点而言, 转移脉冲大小和转移时间长短呈相反的对应关系, 即转移脉冲低对应转移时间长, 转移脉冲高对应转移时间短。

具体地, 选择其中每段具有代表性的入轨点第41点、第261和第341点做进一步的对比和分析, 画出具备以上特性的单条转移轨道，如图 8所示。图 8中, 黑色轨迹为Lissajous轨道, 蓝色轨迹为自然流形段, 绿色轨迹为摄动流形段, 红色轨迹为直接转移段。各轨道的具体数据对比如表 3所示。

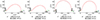thumbnail 图8

不同特性的转移轨道

结合图 8和表 3可以看出, 影响转移脉冲的主要因素为借力脉冲ΔvLFB的大小, 直接转移段时间tPM的长短与转移脉冲没有必然的联系。该特性更适用于航班化运输的多任务性, 即在不严格约束航天器从地球到月球的转移时间情况下, 允许在同一能耗级的低能转移轨迹增多, 使得在同一时间段内低能耗转移的发射窗口增加。此外, 入轨点为第226~360点之中转移脉冲较低但转移时间长的主要原因为自然流形段时间较长。

总体而言, 不同Lissajous轨道入轨点均存在转移脉冲在3.45 km/s左右的可选择区域。考虑载物运输转移脉冲和时间均衡的需求, 宜选择到达Lissajous轨道入轨点为1~65点的转移轨道, 且借力点高度越低越好。但对于航班化运输网络的构建, 可放宽转移时间代价而扩大允许到达的Lissajous轨道入轨点范围至225点, 从而增加发射窗口。

表3

不同转移轨道的数据对比

3.3 Lissajous轨道幅值的影响

将不同幅值下的Lissajous轨道的第一圈轨迹离散为181个入轨点, 借力高度约束条件均设置为100 km。得到固定幅值Ay=5 000 km, Az在[5 000, 35 000]km之间均匀变化; 固定幅值Az=5 000 km, Ay在[5 000, 35 000]km之间均匀变化; 幅值Ay, Az同时在[5 000, 35 000]km之间均匀变化3种情况下的转移脉冲特性变化图，如图 9所示。从图 9可以看出, 对于所选Lissajous轨道入轨点, 固定Lissajous轨道幅值Az=5 000 km时, 随着Ay的增大, 转移脉冲有所减小; 幅值Ay, Az同时增大时, 转移脉冲呈锯齿状减小。总体而言, 随着Lissajous轨道水平和垂直振幅的增加, 绝大部分转移轨道的转移脉冲不超过3.5 km/s。可见, 本文所提出的方法能够实现在未明显增加转移脉冲的情况下, 扩展到达Lissajous中转站轨道的幅值范围。对于转移脉冲不超过3.5 km/s的转移轨道, 其转移时间特性如表 4所示。

thumbnail 图9

不同Lissajous轨道幅值的转移脉冲变化

表4

不同Lissajous轨道幅值的转移时间范围

3.4 星历模型下其他天体的影响

考虑太阳、金星、水星等天体的引力，星历表选择为DE430，出发历元选择为“2025-01-01 00∶00∶00”，选取分布为1∶40∶361的10个Lissajous中转站轨道入轨点。固定借力高度约束均为100 km，采用多重打靶法将CRTBP下的转移轨道转换至精确星历模型中，研究了180 d内发射窗口对应的转移脉冲变化，如图 10所示。

thumbnail 图10

出发历元时间轴向后180 d的转移脉冲分析

结果表明，对不同Lissajous入轨点而言，其他天体的引力对转移脉冲的利弊影响与出发历元有较大关系，变化周期为25 d左右, 约为月球相对地球的运动周期。以轨道入轨点为81点为例，CRTBP模型中转移脉冲为3.47 km/s，星历模型中最优转移脉冲为3.45 km/s，最大转移脉冲为3.71 km/s。从图 10可以看出，在180 d内，Lissajous轨道各入轨点均存在较大范围的最优转移发射窗口，为后续转移任务的窗口选择提供了参考。

4 结论

本文针对基于地月空间Lissajous中转站的低能转移轨道设计与优化问题，给出了流形拼接代替传统脉冲入轨的改进策略，并采用了双层优化方法进行求解，重点研究了借力方位类倾角、借力高度、入轨点位置等对转移轨道特性的影响，结论如下：

1) 采用流形拼接形式改进传统三脉冲转移中的入轨机动，对部分轨道入轨点可降低18~400 m/s左右的转移脉冲，增大了有效入轨点的可选范围；中转站幅值在5 000~35 000 km之间变化的绝大部分转移脉冲不超过3.5 km/s，说明所提出的方法可扩展到达Lissajous中转站轨道的幅值范围。

2) 借力方位类倾角对转移轨道的转移脉冲和时间影响较大，类倾角在[-30 °, 30 °]之间变化，转移脉冲的变化区间为[3.3, 3.8]km/s。类倾角在15 °左右时，转移脉冲较低，约为3.45 km/s。对大部分入轨点而言，借力高度越低，转移脉冲越小，借力效果越好，但转移时间随借力高度无明显变化，而与轨道入轨点位置呈分层变化。

3) 星历模型下，其他天体引力对转移轨道特性的影响与出发历元的关系较大，其中转移脉冲的变化周期为25 d左右，约为月球相对地球的运动周期，180 d内转移脉冲较小的允许发射窗口较广。

以上优化设计方法与结论分析，为未来地月空间航班化运输网络中转站轨道的选取和低能转移轨道的发射窗口和入轨点等参数设计提供了参考。本文中借力方位只考虑了类倾角，后续可考虑类升交点赤经等因素进行全局优化。

References

  1. BAO Weimin, WANG Xiaowei. Some thoughts about cislunar exploration and exploitation[J]. Journal of Astronautics, 2022, 43(6): 705–712 (in Chinese) [Google Scholar]
  2. ZHANG Yulin, LIU Hongwei, JIANG Chaoet al.. Several engineering and technical issues in the development of cislunar space[J]. Journal of Astronautics, 2023, 44(4): 612–632 (in Chinese) [Google Scholar]
  3. KUTTER B F, SOWERS G F. Cislunar-1000: transportation supporting a self-sustaining space economy[C]//AIAA Space and Astronautics Forum and Exposition, Long Beach, 2016 [Google Scholar]
  4. FULLER S, LEHNHARDT E, ZAID C, et al. Gateway program status and overview[J]. Journal of Space Safety Engineering, 2022, 9(4): 625–628 [Article] [Google Scholar]
  5. SOLDINI S, MASDEMONT J J, GOMEZ G. Dynamics of solar radiation pressure-assisted maneuvers between Lissajous orbits[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(4): 769–793 [Article] [Google Scholar]
  6. DUAN X, GOMEZ G, MASDEMONT J J, et al. A picture of solar-sail heteroclinic enhanced connections between Lissajous libration point orbits[J]. Communications in Nonlinear Science and Numerical Simulation, 2020, 85105252 [Article] [Google Scholar]
  7. DUAN Xun, YUE Xiaokui. Research on the Lissajous trajectory transfer of large area mass ratio solar sail spacecraft[J]. Journal of Northwestern Polytechnical University, 2020, 38(5): 1054–1062 (in Chinese) [Google Scholar]
  8. SHIROBOKOV M, TROFIMOV S, OVCHINNIKOV M. Survey of station-keeping techniques for libration point orbits[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(5): 1085–1105 [Article] [Google Scholar]
  9. DU C R, SONG L J, ZHANG J Y, et al. A novel calculation method for low-thrust transfer trajectories in the Earth-Moon restricted three-body problem[J]. Aerospace Science and Technology, 2024, 147: 109048 [Article] [Google Scholar]
  10. DU C R, ZHANG J Y, SONG L J, et al. Optimal design and tracking control of low-thrust orbit transfers between planar and vertical Lyapunov orbits[J]. IEEE Trans on Aerospace and Electronic Systems, 2024, 60(4): 5395–5405 [Article] [Google Scholar]
  11. ZHANG J Y, YU H C, DAI H H. Overview of Earth-Moon transfer trajectory modeling and design[J]. Computer Modeling in Engineering & Sciences, 2023, 135(1): 5–43 [Google Scholar]
  12. ZHANG Chen, ZHANG Hao. Lunar-gravity-assisted low-energy transfer from Earth into distant retrograde orbit(DRO)[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(2): 268–279 (in Chinese) [Google Scholar]
  13. LI Mingtao. Low energy trajectory design and optimization for collinear libration points missions[D]. Beijing: Center for Space Science and Applied Research of CAS, 2010 (in Chinese) [Google Scholar]
  14. RAUSCH R R. Earth to halo orbit transfer trajectories[D]. West Lafayette: Purdue University, 2005 [Google Scholar]
  15. PARKER J S, BORN G H. Direct lunar halo orbit transfers[J]. The Journal of the Astronautical Sciences, 2008, 56(4): 441–476 [Article] [Google Scholar]
  16. ALESSI E M, GOMEZ G, MASDEMONT J J. Two-manoeuvres transfers between LEOs and Lissajous orbits in the Earth-Moon system[J]. Advances in Space Research, 2010, 45(10): 1276–1291 [Article] [Google Scholar]
  17. SANTOS L B T, SOUSA-SILVA P A, TERRA M O, et al. Optimal transfers from Moon to L2 halo orbit of the Earth-Moon system[J]. Advances in Space Research, 2022, 70(11): 3362–3372 [Article] [Google Scholar]
  18. ZHENG Y, PAN B F, TANG S. A hybrid method based on invariant manifold and chaos control for Earth-Moon low-energy transfer[J]. Acta Astronautica, 2019, 163145–156 [Article] [Google Scholar]
  19. FOSSA A, BUCCHIONI G, BLAZQUEZ E, et al. Two and three impulses phasing strategy with a spacecraft orbiting on an Earth-Moon NRHO[J]. Acta Astronautica, 2022, 198669–679 [Article] [Google Scholar]
  20. BUCCHIONI G, LIZY-DESTREZ S, VAUJOUR T, et al. Phasing with near rectilinear halo orbits: design and comparison[J]. Advances in Space Research, 2023, 71(5): 2449–2466 [Article] [Google Scholar]
  21. TROFIMOV S, SHIROBOKOV M, TSELOUSOVA A, et al. Transfers from near-rectilinear halo orbits to low-perilune orbits and the Moon's surface[J]. Acta Astronautica, 2020, 167: 260–271 [Article] [Google Scholar]
  22. BURY L, MCMAHON J W. Landing trajectories to moons from the unstable invariant manifolds of periodic libration point orbits[C]//Proceedings of the AIAA Scitech 2020 Forum, Orlando, 2020 [Google Scholar]
  23. DU C R, STARINOVA O L, LIU Y. Transfer between the planar Lyapunov orbits around the Earth-Moon L2 point using low-thrust engine[J]. Acta Astronautica, 2022, 201: 513–525 [Article] [Google Scholar]
  24. DU C R, STARINOVA O L, LIU Y. Low-thrust transfer dynamics and control between halo orbits in the Earth-Moon system by means of invariant manifold[J]. IEEE Trans on Aerospace and Electronic Systems, 2022, 59(4): 3452–3462 [Google Scholar]
  25. GORDON D P. Transfers to Earth-Moom L2 halo orbits[D]. West Lafayette: Purdue University, 2008 [Google Scholar]
  26. ZENG H, ZHANG J R. Design of impulsive Earth-Moon halo transfers: lunar proximity and direct options[J]. Astrophysics and Space Science, 2016, 3611–17 [Article] [Google Scholar]
  27. ZENG Hao, LI Zhaoyu, PENG Kun, et al. Research on application of Earth-Moon NRHO and DRO for lunar exploration[J]. Journal of Astronautics, 2020, 41(7): 910–919 (in Chinese) [Google Scholar]
  28. SZEBEHELY V. Theory of orbit: the restricted problem of three bodies[M]. New York: Academic Press Inc, 1967 [Google Scholar]
  29. JIN Y, XU B. Three-maneuver transfers from the cislunar L2 halo orbits to low lunar orbits[J]. Advances in Space Research, 2022, 69(2): 989–999 [Article] [Google Scholar]
  30. RICHARDSON D L. Analytic construction of periodic orbits about the collinear points[J]. Celestial Mechanics, 1980, 22(3): 241–253 [Article] [Google Scholar]
  31. MASDEMONT J J. High-order expansions of invariant manifolds of libration point orbits with applications to mission design[J]. Dynamical Systems, 2005, 20(1): 59–113 [Article] [Google Scholar]
  32. AKSENOV S, BOBER S, GUSKOVA M. Mapping of initial conditions for libration point orbits[J]. Advances in Space Research, 2021, 68(6): 2501–2514 [Article] [Google Scholar]
  33. HOWELL K C, PERNICKA H J. Numerical determination of Lissajous trajectories in the restricted three-body problem[J]. Celestial Mechanics, 1987, 41(1/2/3/4): 107–124 [Google Scholar]
  34. LI M T, ZHAENG J H. Impulsive lunar halo transfers using the stable manifolds and lunar flybys[J]. Acta Astronautica, 2010, 66(9/10): 1481–1492 [Google Scholar]
  35. LI M T, ZHENG J H. Indirect transfer to the Earth-Moon L1 libration point[J]. Celestial Mechanics and Dynamical Astronomy, 2010, 108203–213 [Article] [Google Scholar]
  36. MARCHAND B G, HOWELL K C, WILSON R S. Improved corrections process for constrained trajectory design in the N-body problem[J]. Journal of Spacecraft and Rockets, 2007, 44(4): 884–897 [Article] [Google Scholar]

All Tables

表1

流形拼接段优化变量的取值范围

In the text
表2

直接转移段优化变量的取值范围

In the text
表3

不同转移轨道的数据对比

In the text
表4

不同Lissajous轨道幅值的转移时间范围

In the text

All Figures

thumbnail 图1

圆型限制性三体模型示意图
In the text
thumbnail 图2

Lissajous轨道及其内部不变流形
In the text
thumbnail 图3

转移轨道示意图
In the text
thumbnail 图4

Lissajous轨道离散示意图
In the text
thumbnail 图5

流形拼接段转移脉冲、转移时间与自然流形时长曲线
In the text
thumbnail 图6

不同入轨点和类倾角的转移脉冲与转移时间变化图
In the text
thumbnail 图7

不同入轨点和借力高度的转移脉冲与时间的变化能图
In the text
thumbnail 图8

不同特性的转移轨道
In the text
thumbnail 图9

不同Lissajous轨道幅值的转移脉冲变化
In the text
thumbnail 图10

出发历元时间轴向后180 d的转移脉冲分析
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.