| Issue |
JNWPU
Volume 39, Number 1, February 2021
|
|
|---|---|---|
| Page(s) | 159 - 166 | |
| DOI | https://doi.org/10.1051/jnwpu/20213910159 | |
| Published online | 09 April 2021 | |
Fast guidance method of lunar landing based on dynamic programming
基于动态规划的月面定点着陆快速制导方法
1
School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
2
National Key Laboratory of Aerospace Flight Dynamic, Xi'an 710072, China
Received:
8
May
2020
In this paper, a novel multi-stage trajectory transfer and fixed-point landing time optimal guidance method for the lunar surface emergency rescue mission is proposed. Firstly, the whole process motion and dynamics model for the lunar surface emergency rescue with four stages are established. Then, in the initial orbit transfer phase, the Lambert algorithm based on "prediction + correction" is designed for the non spherical gravitational perturbation of the moon. In the powered descent phase, the Hamiltonian function is used to design a time suboptimal explicit guidance law that can be applied in orbit in real time. Finally, aiming at the multi-stage global time optimal guidance, the whole time process guidance law is obtained by establishing the allowable control set for each stage in the whole process. The simulation results show that compared with the piecewise optimal control method, the present method has better optimization effect and shorter whole process time. It is of great significance to the possible emergency rescue mission of manned lunar exploration in the future.
摘要
提出了一种面向月面紧急救援任务的多阶段轨道转移与定点着陆全程时间最优制导新方法。建立了包含4个阶段的月面紧急救援全程运动及动力学模型。在初轨转移段,设计了在月球非球形引力摄动下基于"预测+校正"的Lambert算法。在动力下降段,利用哈密尔顿函数设计了一种可在轨实时应用的时间次优显式制导律。针对多阶段全局时间最优制导问题,通过对全程各段建立允许控制集,采用动态规划法得到了全程时间最优的制导律。仿真结果表明该方法相比于分段最优控制方法优化效果更好,全过程用时更短,对未来载人月球探测过程可能出现的月面紧急救援任务具有重要意义。
Key words: moon emergency rescue / lambert algorithm / powered descent phase / dynamic programming method
关键字 : 月面紧急救援 / Lambert算法 / 动力下降段 / 动态规划法
© 2021 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
月球是距离地球最近的天体,也是空间科学研究最重要的天体之一。从20世纪50年代开始就有各类航天器对月球进行探测。1961年至今,以美国、欧空局、中国、日本、印度等为代表的世界主要航天大国和组织开始制定各自的载人登月计划,其中以美国2019年最新提出的"阿耳忒弥斯"载人月球探测计划为代表。载人登月的下一步是建立月球基地,目前各国提出了不同的月球基地方案,其中以“门德尔计划”为代表[1]。载人登月是一项极为复杂的系统工程,一旦某些环节出现问题宇航员将在月表处于危险之中。同时由于地月距离遥远,宇航员无法等到地球再次发射航天器进行救援,所以需要设计一种部署在环月球轨道的救援航天器。
目前针对该类面向月球紧急救援任务的制导规划研究较少。传统轨道规划主要考虑燃料最优,而对于紧急救援任务需要考虑时间最优, 是本文与传统方法的本质区别。本文首先对该类航天器的工作模式进行假设:航天器分为轨道舱和救援舱两部分,首先由初始轨道经轨道转移到达任务轨道,下降轨道高度,经一段时间调整后星下点到达救援点附近。随后释放着救援舱,经制动下降软着陆于月表,投放救援物资,轨道舱则留在任务轨道为救援舱提供导航与通讯。
本文研究的制导问题是一种终端时间自由且带有条件约束的非线性最优化控制问题,其分为4个阶段,即初轨段、初轨转移段、任务轨道调相、动力下降段,其中需要在第2、4段设计轨道转移制导、制动段软着陆制导,在第1、3段仅进行轨道保持控制,最后设计基于动态规划法的全局最优制导律。
目前,轨道转移制导主要分为连续推力制导和脉冲推力制导2类[2-3]。连续推力制导为非线性规划问题,使用遗传算法、伪谱法和差分进化算法等进行求解,其控制复杂,对推力器经度要求高[4]。脉冲推力制导主要以两脉冲Lambert轨道转移为代表,求解动力学方程的边值问题,从而确定2次的脉冲,其控制简单,对单次推力大小要求较高[5]。
目前,软着陆制导的方法主要分为重力转弯制导、标称轨迹制导和闭环显式制导3类[6]。重力转弯制导方法简单可行,但无法进行时间和燃料优化[7]。标称轨迹制导理论上可实现燃耗最优,但考虑到软着陆时间较短和星载计算机能力限制使其难以实现[8]。显式制导方法根据着陆器的运动状态,按照泛函的显函表达式实时计算控制量的制导方法。该方法物理意义明确,实时性好,但鲁棒性需要提高[9]。
目前,关于月球软着陆的轨道转移优化方法、制动下降段优化方法均研究较多,但是将整个着陆过程整体优化的研究较少。本文研究点在于对月面紧急救援任务,设计了一种全程时间最优的制导律。本文从全程时间最优的角度对制导过程进行分析和建模。首先采用普适变量法对月球引力摄动下的单圈Lambert轨道转移问题进行分析,而后采用改进显式制导方法解决了动力下降段制导问题,并提出允许控制数据库的概念。最后采用动态规划法,从已建立的全程各段控制集中优化选择各阶段初末条件实现制导过程的全局时间最优。
1 问题描述
救援航天器的工作分为4个阶段:①在接到救援指令后,在100 km环月待命圆轨道上移动到轨道转移的起始点;②采用双脉冲Lambert轨道转移的模式,从待命轨道机动进入15 km任务圆轨道;③在任务轨道上飞行一段时间,使接近救援点,该任务轨道上应仅有一个点距离待救援最近;④在任务轨道上释放着救援舱,经动力段制导,下降高度到达软着陆前2 km悬停点。
在紧急救援着陆过程中存在三步决策, 分别是离开初始轨道时的位置、进入任务轨道的位置、离开任务轨道的位置。每一阶段的终态都是下一阶段的初始状态, 同时每一阶段都存在一定约束, 这导致了紧急救援的时间优化问题是一个强耦合、非线性的问题。对该问题决策变量可选为初轨段时间Δt1、初轨转移段时间Δt2、初轨转移段结束点状态X2和任务轨道段时间Δt3, 在确定上述决策变量的基础上就可以通过数值积分获得航天器每时刻状态和制动下降段时间Δt4。
对全过程优化定义为: 给定初始点状态X0和待救援点位置Xf, 在满足各阶段约束的情况下, 求取优化决策变量Δt1, Δt2, X2, Δt3以完成任务。对于多步优化问题, 采用动态规划法求解可以降低算法时间复杂度。
2 月球非球形摄动下的Lambert轨道转移
2.1 轨道转移动力学模型
如图 2a)所示, 设O-XYZ为惯性坐标系, O位于月心, OZ指向初始航天器方向, OX在环月轨道平面内, 指向前进方向, OY由右手定则确定, 构成直角坐标系。φ, θ分别表示发动机推力在轨道坐标系下的方向角和俯仰角, 发动机推力引起的速度增量在惯性系下的三轴分量分别为Δu, Δv, Δw, 航天器状态向量P(x, y, z, u, v, w) 均在月心惯性系下表示。
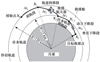 |
图1 救援航天器工作模式示意图 |
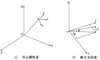 |
图2 坐标系和变量定义 |
本文基于二体问题和开普勒轨道假设, 将Lambert问题改进为固定时间(tf) 约束下, 已知初末状态向量P0, Ptf, 求解2次轨道转移脉冲的两点边值问题。其动力学方程为
式中, μ为月球引力常量, r为轨道半径。由于采用脉冲推力轨道转移, 状态量在边界发生突变, 该运动学方程输入的边界值i0, itf由(2)式确定
式中: i0-, itf-(i=u, v, w)分别表示第一、二次施加脉冲前速度; Δi0, Δitf分别为2次施加的速度脉冲。
在Lambert轨道转移中边界条件由执行任务时的初始状态和目标点的位置决定。对该过程消耗的燃料进行分析, 令Q=Ispge则
式中: Isp为发动机比冲; ge为地球引力常数; Q为单位推进剂产生的冲量; m0, mtf为2次轨道转移前的质量; Δm0, Δmtf为2次轨道转移消耗推进剂质量。
上述(1)~(4)式构成了轨道转移动力学模型, 该类问题可通过构建普适变量时间方程, 使用Newton迭代法进行求解, 本文不再赘述[10]。
2.2 月球非球形摄动下的制导律设计
对于月球而言, 其非球形摄动的J2, J22项影响最大, 月球引力位函数在惯性系下形式如下[11]
式中: Clm, Slm为非归一化谐系数; Plm为缔合勒让德函数; λG, ϕ为月心经纬度。对于月球引力的J2项C2, 0=-8.475 05×10-4, S2, 0=0, 对于月球引力的J22项C2, 2=8.417 75×10-5, S2, 2=4.960 53×10-5。
考虑摄动后的航天器运动学模型为
式中, gradU为月球引力位梯度。
对于远距离变轨, 航天器受摄运动的结果可以最终表示为脱靶量, 定义等时交会点Ptf*为航天器预定转移时间后到达的位置与速度矢量。其与期望交会点状态Ptf之间的矢量差为脱靶矢量Lm
综合(1)~(7)式本文构建了一种迭代算法对其进行修正, 如图 3所示。在已知r0-, rtf和tf的前提下, 可以求解出对应的速度增量和燃料消耗。
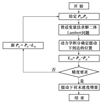 |
图3 受摄动Lambert问题求解流程 |
记录每种状态下的容许转移控制, 建立轨道转移数据库, 即所有容许控制的集合, 而后采用动态规划的方法从数据库中选出最优控制集合, 以实现对全程最优解的确定。
3 制动段制导律设计
3.1 制动段动力学模型
设O′-XYZ为原点在月心的惯性坐标系, O′Z轴指向动力下降段起始点, O′X轴位于v和O′Z轴所确定的平面内, 垂直于O′Z轴, 指向速度方向为正; O′Y轴服从右手法则。设o-xyz为原点在着陆点的着陆场坐标系, oz轴沿O′o方向背离月心为正, ox轴垂直于oz轴指向运动方向为正; oy轴服从右手法则。忽略月球自转, 在整个制导过程中, 视月球重力加速度为常值。则在着陆场坐标系中, 动力学模型可近似表示为[12]
式中: ax, ay, az分别为着陆场坐标系下的三轴加速度分量; φ, Φ为制动力的俯仰角和方向角; gL为月球重力加速度, 视为常数。发动机为液体燃料, 全程工作, 比冲一定[12]。
3.2 最优制动段制导律设计
救援舱状态矢量为X=[x y z u v w]T其控制变量为U(t)=[ax ay az]T, U(t)∈U⊂Rm, t∈[0, tgo], 则状态方程可以写为
本文根据发动机等加速度且全程工作的假设, 引入如下性能指标, 将下降段时间最优问题转化为能量消耗最优问题, 在能量最优显式制导控制[13]的基础上进行求解。
这样, (8)~(10)式就构成了一个最优控制问题, 在最短的tgo内通过容许控制角[φ Φ]T, 使救援舱到达期望状态。由极大值原理, 引入哈密尔顿函数
式中: λ为协态变量, 由共轭方程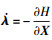 计算得到
计算得到
由最优性条件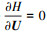 , 可得
, 可得
将(13)式带入(8)式积分求解可以得到协态变量的中间参数(λ10, λ20, λ30, λ40, λ50, λ60)的表达式, 进而得到每时刻三轴方向需要的加速度
通过最优控制的三轴加速度反推最优控制的俯仰角和方向角为
实际推力可以表示为
对于剩余时间tgo的求解, 考虑到对于初始位置运行到末端位置的初始时间的不确定性, 但由于最优控制原理始终成立H|t=tgo=0, 则
则tgo的解析表为
tgo可以由上述四次方程解析获得, 这样(14)~(16)式和(18)式就构成了一组最优制导律。在给定着陆的初末位置时, 就可以计算这种状态下最优轨迹和时间消耗, 并建立动力下降段允许控制数据库, 为全局最优的制导律提供数据支撑。
4 全局动态规划法
本文二、三部分的分析, 着重于紧急救援航天器第②、④阶段的制导律设计, 在每个阶段中给定相应条件即可得到制导轨迹和飞行时间。在初轨段和任务轨道调相段的飞行时间可以由下式确定
式中: δ1, δ2为进入和离开任务/初始轨道时刻所对应的真近点角; χ为任务/初始轨道角速度。
同时, 在全过程还要考虑到如下过程约束
式中: “*”项表示航天器最大容许量; μF表示燃料质量因数; 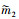 表示动力下降段每时刻质量; Δt2为动力下降段时间。此外, 救援舱在任务轨道上移动的相位应大于50°, 以保证轨道转移后的稳定控制。
表示动力下降段每时刻质量; Δt2为动力下降段时间。此外, 救援舱在任务轨道上移动的相位应大于50°, 以保证轨道转移后的稳定控制。
对于多约束优化问题, 采用动态规划法求解。其主要原理是不论第一段采取何种决策, 第二段以后的决策序列都对第一段产生的状态是一个最优决策。动态规划法的时间复杂度相较于遍历搜索法的O(n!)降低到了O(n2), 更便于在轨计算[14]。其具体实现步骤为:
step1 为实现月面紧急救援, 取如下表示全程用时最短的性能指标函数
式中: uk为k阶段允许控制集; dk(uk)为从k阶段的uk选择的控制对应的时间。
step2 对于动力下降段决策, 输入待救援点位置Xf、任务轨道调相段结束状态X3, 利用(14)至(16)式、(18)式获得制动段允许控制集, 定义f1(E)为各X3对应的最短转移时间。
step3 对于任务轨道调相段, 输入状态X2, X3, 利用(19)式获得允许控制集, 定义f2(Di)为各X2状态到救援点的最短时间。
step4 对于初轨转移段, 输入状态X1, X2, tf, 利用图 3的受摄动Lambert问题求解流程获得转移段允许控制集, 定义f3(Cj)为各X1到救援点的最短时间。
step5 对于初轨段采用和step3相同的方法, 获得初始点X0到救援点的最短时间, 即全局最优解。
式中, u1, u2, u3, u4为上文建立的符合各阶段条件约束的允许控制数据库。
有别于传统航天多阶段任务的经验决策, 通过上述迭代递推的方法的各阶段控制, 使之在全局上时间最优。所述的各阶段允许控制集是满足(20)式约束的有限集合, 其集合的大小可根据所需的求解精度确定。
5 仿真验证
采用计算机数值仿真方式进行验证, 轨道积分采用ode45变步长方法。假定某月面紧急救援任务的初始条件为: 月球引力常数μ=4 903 km3/s2, r=1 738 km, 救援航天器总体质量为3 000 kg, 其燃料质量因数为μF1=0.3, Isp=350 s, 初始轨道为i=0的120 km高度的圆轨道, 位于月球经纬坐标系下(0°N, 100°W), 任务轨道高度为15 km, 释放的救援舱质量为1 000 kg, Isp2=300 s, μF2=0.4, 待救援点在月球经纬坐标系下为(10°N, 20°E)。设在任务过程4个阶段的用时分别为Δt1, Δt2, Δt3, Δt4, 各阶段的允许控制集合构建时按位置精度为轨道倾角与月心角1°, 时间精度1 s进行仿真。图 5至9分别表示各阶段的允许控制集。
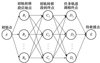 |
图4 动态规划法网络图 |
 |
图5 Δt1, Δt3与在轨运行月心角的关系 |
 |
图6 Lambert转移燃料消耗与入轨位置 |
 |
图7 转移段允许控制集 |
 |
图8 制动段允许数据集 |
 |
图9 动力下降段控制推力方向角随时间变化 |
由图 5可知Δt1, Δt3与航天器在轨道运行经过的月心角的关系, 在二体模型下其运行时间与月心角呈线性关系, 在任务轨道上运行相同的月心角所用的时间相对较短, 这是由于其轨道高度较低。为了实现救援航天器的快速着陆, 尽可能多地在任务轨道时运行。
图 6表示引力摄动下Lambert轨道转移所消耗的燃料质量与初末位置经过的月心角Δθ和给定转移时间tf有关。在一定的Δθ下, 燃料消耗随tf的增加先减小后增大, 总存在一个极小值, 当目标轨道倾角和升交点赤经变化时, 燃料消耗和Δθ与tf的关系时相似的。
图 7表示在轨道转移部分段允许控制集, 取燃料消耗恰满足约束的最短转移时间的控制作为允许控制。最短转移时间tf随目标轨道升交点和运行的月心角Δθ增大而增大, 随轨道倾角Δi变化不明显。
图 8表示救援舱不同位置进入动力下降段到救援点所消耗的时间, 其中轨道倾角和经度表示航天器进行下降段制导的初始位置。可知初始经度越靠近目标, 则所用的时间将会非线性的减小, 越晚离轨则时间减少的越多, 而下降段时间对轨道倾角不敏感。在燃料允许条件下, 最短着陆时间为353.9 s。
将建立的关于Δt1, Δt2, Δt3, Δt4的允许控制数据库带入到(21)~(25)式的动态规划法递推方程中, 用文献[17]中求解方法计算得到救援航天器各阶段的控制[15]。
其中在Lambert转移段施加的第一次脉冲为ΔV1=(-437.26, 384.78, 255.91)T m/s燃料消耗553.25 kg, 第二次脉冲为ΔV2=(258.87, -403.98, 5.55)T m/s燃料消耗346.75 kg。从表 1中可以看出, 全局最优控制的结果并不是各阶段最优控制的简单叠加, 采用本文的算法救援航天器共用时2 322.32 s, 消耗燃料质量为1 257.5 kg, 且满足各阶段的性能要求。
基于动态规划的控制结果
图 9分析了在制动段其发动机的俯仰角和方向角随时间变化情况, 从仿真结果可以看出, 着陆器在该显式制导律作用下可以准确安全地到达目标着陆点, 速度同时减小为零。φ的变化范围较小, 用于减速, Φ用于调整方向。在前347 s 2个推力方向角变化都比较平缓, 在347 s后Φ发生了抖振, 这是由于随着目标的接近, (14)式中的tgo减小, 引起的加速度发散, 解决方法为临近目标上空时按惯性飞行或设计临近目标时的制导律。
在以往的工程设计中, 通常将优化问题在各阶段分别考虑, 导致无法得到总体最优的结果, 现假设两种局部最优设计思想与本文总体优化方法对比分析。局部优化方案Ⅰ: 考虑初轨段时间最短, 即当接收到救援指令后立刻进行轨道转移, 其余3个阶段按本文方法设计; 局部优化方案Ⅱ: 考虑初轨转移段时间最短, 即在燃料允许的范围内进行变轨时间最短的轨道转移, 其余3个阶段按本文方法设计。
将这2种可能的设计情况在不同待救援点下与本文的全局最优方法对比, 得到全局最优控制优化效果优于传统设计, 采用全局优化方法的任务全过程时间更短, 在3种工况下分别最多减少了4.07%,2.82%,3.41%。
3种设计方法在不同工况下的比较
6 结语
在月球表面实施多约束的精确制导快速救援,是未来保证月球探测开发领域广受关注的研究热点。本文基于全局优化的最优控制方法给出了月面救援控制的一般设计流程,并进行了数值验证,实现了时间最优着陆任务,满足了过程中的多约束。结果表明, 该方法完全满足月球快速软着陆任务的精确性和安全性要求, 为今后的研究提供参考。
References
- Bonneville R. A Truly international lunar base as the next logical step for human spaceflight[J]. Advances in Space Research, 2018, 61(12):2983–2988 [Article] [Google Scholar]
- LI Bin. Research on the reachability method of impulse thrust orbit maneuver[D]. Changsha: National University of Defense Science and Technology, 2015 (in Chinese) [Google Scholar]
- SUN Chong. Orbit design of spacecraft under continuous small thrust[D]. Xi'an: Northwest Polytechnic University, 2017 (in Chinese) [Google Scholar]
- Wang Shi, Zhu Kaijian, Dai Jinhai, et al. Time-energy optimization of orbit transfer by evolutionary algorithm[J]. Acta Astronautica, 2002, (1):73–75 [Article] (in Chinese) [Google Scholar]
- Zhuang Xuebin, Zhang Yaolei, Li Jun, et al. Method of fast fixed-point orbit transfer based on two- impulse lambert[J]. Missiles and Space Vehicles, 2015, (3):1–4 [Article] (in Chinese) [Google Scholar]
- Qiao Yandi. Research on guidance algorithm of lunar probe for soft landing[M]. Harbin: Harbin Institute of Technology, 2018 (in Chinese) [Google Scholar]
- Danchick R. Connecting gravity turn guidance dynamics to near planar missile motion geometry[J]. IET Radar, Sonar & Navigation, 2016, 10(2):278–284 [Google Scholar]
- Likhachev V N, Yu A, Sikharulidze G, et al. Main braking phase for a soft moon landing as a form of trajectory correction[J]. Solar System Research, 2013, 47(7):77–84 [Article] [Google Scholar]
- Zheng G, Nie H, Chen J B, et al. Dynamic analysis of lunar lander during soft landing using explicit finite element method[J]. Acta Astronautica, 2018, 148: 69–81 [Article] [Google Scholar]
- Peng Kun, Xu Shijie. A nonsingular universal variable method for lambert orbit change[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(4):399–402 [Article] (in Chinese) [Google Scholar]
- Wang Yi, Xing Jianjun, Zheng Liming, et al. Autonomous determination of lunar gravity constant and coefficient of the lunar J2 perturbation based on adaptive Kalman filter[J]. Journal of Astronautics, 2015, 36(7):777–783 [Article] (in Chinese) [Google Scholar]
- LIU Haomin. Research on guidance and control for soft landing on lunar at main braking phase[D]. Harbin: Harbin Institute of Technology, 2007 (in Chinese) [Google Scholar]
- Mondal S, Padhi R. Generalized explicit guidance with optimal time-to-go and realistic final velocity[J]. Proceedings of the Institution of Mechanical Engineers, 2019, 233(13):4926–4942 [Article] [Google Scholar]
- Bonny T, Ridhwan A D, Mohamed B A. Time efficient segmented technique for dynamic programming based algorithms with FPGA implementation[J]. Journal of Circuits, Systems and Computers, 2019, 28(13):195–227 [Google Scholar]
- Zhu Yuhua, Zhuang Dianzheng. Modern control theory[M]. Beijing: Mechanical Industry Press, 2018 (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 救援航天器工作模式示意图 |
| In the text | |
 |
图2 坐标系和变量定义 |
| In the text | |
 |
图3 受摄动Lambert问题求解流程 |
| In the text | |
 |
图4 动态规划法网络图 |
| In the text | |
 |
图5 Δt1, Δt3与在轨运行月心角的关系 |
| In the text | |
 |
图6 Lambert转移燃料消耗与入轨位置 |
| In the text | |
 |
图7 转移段允许控制集 |
| In the text | |
 |
图8 制动段允许数据集 |
| In the text | |
 |
图9 动力下降段控制推力方向角随时间变化 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


