EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 419-427 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 419 - 427
DOI https://doi.org/10.1051/jnwpu/20254330419
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

齿轮传动涡扇发动机(geared turbo fan engine, GTF)是一种大推力高涵道比新型涡扇发动机, 其核心技术之一是在发动机风扇与低压涡轮转子间安装了滑动轴承支承的星型齿轮传动系统, 使风扇和低压压气机各自在其高效转速范围内运转[1-2]。由低压压气机输入的动力先后通过太阳轮、若干行星齿轮、齿圈的啮合传动分流与汇流, 最终将动力输出至风扇转子。在GTF星型齿轮传动系统中, 行星齿轮内孔轴瓦与行星齿轮支承轴颈组成了滑动轴承, 其结构特点是轴瓦随行星齿轮转动, 而作为支承的行星齿轮轴固定不动。GTF星型齿轮系统传动功率很大, 使得GTF滑动轴承在高转速、高比压和大偏心条件下工作。为了满足高承载力需求, 滑动轴承间隙比设计的比较小, 这种结构和工况特征对GTF滑动轴承性能提出了严苛要求[3-4]。

在高转速、高比压和大偏心工况下运行的GTF滑动轴承, 存在着轴颈端部温升和热变形过大的问题。又因轴颈支承柔性等导致轴颈产生倾斜, 不仅使GTF滑动轴承轴颈端部易发生碰磨风险[5], 而且润滑油膜轴向物理场的分布变化使得滑动轴承润滑状态的转捩十分敏感[6-7], 从而表现出GTF轴承运行状态与润滑油膜轴向物理场变化的互构关系[8-11], 即润滑油膜的物理特性(如厚度、压力、温度等)和轴承的运行状态(如偏心率、变形等)存在一种双向互动和相互塑造的动态关系, 这种关系使得系统行为更加复杂且难以通过单一因素来进行预测或分析。因此, 有必要针对高转速、高比压和大偏心工况引致的GTF滑动轴承轴向油膜压力和温度分布不均、轴承端部温升过高和变形过大等润滑油膜轴向物理场开展研究。

本文考虑润滑油温黏效应、轴承热弹性变形和轴颈倾斜等影响, 建立了滑动轴承热弹流润滑分析模型, 对4种轴颈轴向母线的GTF滑动轴承开展了高转速、高比压、大偏心和轴颈倾斜等条件下的性能分析, 通过对比具有不同轴颈轴向母线GTF滑动轴承的性能差异, 优选出油膜轴向物理场均匀化程度较高的轴向母线构型。在此基础上, 以增大油膜承载力、降低油膜温升、以及提升轴向膜厚均匀化程度为目标, 开展轴承结构参数优化, 从而为GTF滑动轴承的轴颈结构设计、几何参数匹配、变形协调分析和轴承性能优化等提供指导。

1 滑动轴承油膜轴向物理场均匀化表征及轴颈轴向母线设计

为了降低轴颈端部油膜破裂或发生碰磨的风险, 需要通过合理设计使轴颈端部的油膜厚度和油膜温度处于安全范围内。润滑油膜轴向的压力和温度的不均匀分布, 反映到轴承结构上是滑动轴承弹性变形和热变形的不均匀, 最终表现为润滑油膜厚度在轴向上的不均匀。因此, 油膜轴向物理场的均匀性主要通过油膜厚度轴向分布的均匀性表征。

滑动轴承发生油膜破裂和碰磨失效风险较高的位置是轴承端部最小油膜厚度处, 为此应保证该截面上的油膜厚度轴向分布满足一定要求, 也即油膜厚度轴向分布中最小值hn_min和最大值hn_max处在一个合理区间使油膜较均匀地承载(见图 1所示)。因此, 本文提出了“油膜轴向均匀化系数”这一参数, 以量化滑动轴承润滑油膜轴向分布(亦即轴向物理场)的均匀化程度, 如(1)式所示。

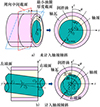thumbnail 图1

不同运行状态下的滑动轴承结构示意图

滑动轴承油膜轴向物理场变化与轴颈轴向形状有很大关系。为了获得均匀化程度较高的油膜轴向物理场, 参考圆柱滚子轴承设计, 选择了4种轮廓曲线分别作为滑动轴承的轴颈轴向母线, 通过对比这4种滑动轴承性能, 选出油膜轴向物理场均匀化程度较高的滑动轴承结构。4种轴颈轴向母线轮廓分别是Reusner对数曲线轮廓[12](简称R型)、Lundberg对数曲线轮廓[13](简称L型)、鼓型曲线轮廓[14]和通用直线轮廓[15], 4种轴颈轴向母线的函数表达式和结构尺寸如图 2所示。

thumbnail 图2

4种轴颈轴向母线函数方程及构型示意图

2 热弹流润滑分析模型

本节考虑润滑油温压黏效应、轴承弹性变形和热变形的影响, 建立滑动轴承热弹流润滑分析模型。

1) 基本控制方程

雷诺方程的一般形式如(2)式所示。

式中: x为周向坐标; y为轴向坐标; p为平均流体压力; h为油膜名义厚度; hT为实际膜厚; η为润滑油的动力黏度; U为滑动轴承轴瓦的线速度。

不计入轴颈表面弹性变形的油膜厚度表达式为

式中: c为半径间隙; e为偏心率; θ为以竖直轴为起点的圆周角度; φ为轴承偏位角。

考虑轴颈倾斜时, 沿轴承轴线在不同y坐标上轴承截面轴心位置均不相同, 如图 1b)所示的轴颈轴线与轴承两端面交点C1和C2, 其位置坐标分别为(x1, 0, z1)和(x2, L, z2)。(3)式中的e和φ是y坐标的函数, 此时偏心距e表示为

式中: 。

忽略轴颈和轴瓦的热传导, 只考虑油流带热引起的表面热变形, 以及轴颈和轴瓦表面弹性变形的滑动轴承油膜厚度表达式为

式中: δp为弹性变形引起的油膜厚度变化; δT为热变形引起的油膜厚度变化。

使用Reynolds边界条件求解(2)式, 对应边界条件表达式为

式中: x*为油膜破裂点位置。

2) 能量方程及边界条件

滑动轴承油膜温度场通过求解油膜能量方程来确定, 如(7)式所示。

式中: ρ为润滑油密度; u, v为润滑油周向流速和轴向流速; T为油膜温度; Cf, Kf分别为润滑油定压比热容和导热系数; η为润滑油动力黏度。

求解能量方程时将滑动轴承轴颈视为等温体, 在轴-润滑油交界处总热流量为零, 且在轴瓦-润滑油交界处满足热通流量连续条件。

3) 润滑油温压黏关系

润滑油黏度、温度、压力之间的关系可表示为

式中: T0为环境温度; η0为环境温度下滑油黏度。

4) 滑动轴承的弹性变形和热变形计算

轴颈外表面和轴瓦内表面上各点在油膜压力作用下产生的弹性变形、在温度作用下产生的热变形均可采用变形矩阵方法进行计算[16]。该方法通过有限元计算得到固体柔度矩阵, 即轴承上各点受单位压力产生的附近节点变形量, 再将实际油膜压力作用在柔度矩阵上, 并将各节点变形量累加即可得到弹性变形量。轴承热变形计算同理。

对于线弹性材料, 通过变形矩阵法计算轴瓦内表面和轴颈外表面弹性变形，如(9)式所示, 热变形计算如(10)式所示。

式中: pij为油膜作用在轴瓦或轴颈节点(i, j)上的实际压力值; Kijrs为作用在节点处的单位油膜压力使节点产生的径向变形量, Tij为油膜温度矩阵节点(i, j)上的实际温度值; Hijrs为作用在节点处的单位油膜温度使节点产生的径向变形量; r=1, 2…m, s=1, 2…n; δp为实际油膜压力作用下轴瓦或轴颈各节点的径向变形量; δT为实际油膜温度作用下轴瓦或轴颈各节点的径向变形量。

5) 滑动轴承性能计算方法

滑动轴承油膜的压力、温度和厚度分布可以使用有限差分法求解前述控制方程获得。其中, 通过超松弛迭代法求解Reynolds方程, 松弛因子取0.7, 经测试当收敛精度ERR取值小于10-4时结果稳定。在此基础上, 滑动轴承承载力通过对油膜压力沿周向积分并由(11)式计算得到。

式中: Fx, Fz分别为油膜支反力在水平与垂直方向上的分量。

滑动轴承端泄流量由(12)式计算得到。

式中：Q1, Q2分别为轴承前端和后端的泄流量, Q1= , Q2= 。

滑动轴承平均摩擦损耗通过将轴颈表面剪切力在整个润滑区域内积分得到, 由(13)式计算得到。

3 轴承热弹流润滑性能分析

本文计算涉及的滑动轴承结构和工况参数如表 1所示。轴颈和轴瓦材料均为锡青铜, 其密度为8 950 kg/m3, 弹性模量为113 GPa。润滑油牌号为飞马二号航空润滑油, 常温下的运动黏度为24.4 mm2/s。

表1

滑动轴承结构和工况参数

3.1 4种轴向母线的滑动轴承性能对比分析

在偏心率为0.8、轴承转速为8 500 r/min、供油温度为27℃的工作条件下, 4种不同轴颈母线的滑动轴承典型性能参数计算结果如表 2所示。可以看出, 直线型轴向母线滑动轴承虽具有较高的承载能力, 但其在最小油膜厚度、温升和摩擦功耗等性能方面的不足也很明显。

表2

不同轴颈母线的滑动轴承润滑性能

与直线型轴向母线滑动轴承相比, 鼓型、R型和L型轴向母线滑动轴承的最大油膜温升由78.41℃分别减小到69.16, 50.21和54.43 ℃, 降幅分别为11.8%, 35.96%和30.58%。原因是R型和L型轴向母线滑动轴承轴向中间截面的轴颈直径明显大于轴端处, 油膜厚度自轴向中间截面向轴端处逐渐增加, 使得对流换热效果显著, 油膜温度分布更加平缓均匀。

与直线型轴向母线滑动轴承相比, 鼓型、R型和L型轴向母线滑动轴承最大油膜压力由32.98 MPa分别降低到27.52, 26.91和27.13 MPa, 降幅分别为16.55%, 18.40%和17.74%。此外, 较之直线型轴向母线滑动轴承, 鼓型、R型和L型轴向母线滑动轴承的承载力则分别降低了14.44%, 19.02%和17.53%。

为了进一步对比4种轴颈轴向母线滑动轴承油膜轴向物理场的差异, 图 3给出了滑动轴承最小油膜厚度所在轴向截面(如图 1所示)的最小油膜厚度分布、最大油膜温度分布和最大油膜压力分布。可以看出, 就润滑油膜轴向物理场均匀性而言, 除直线型轴向母线滑动轴承之外, 其他3种轴向母线滑动轴承的轴向物理场均匀性好得多, 可降低局部变形和油膜厚度剧烈变化导致的碰磨风险。

thumbnail 图3

4种轴向母线滑动轴承的润滑油膜轴向物理场

因此, 可在满足润滑油膜轴向物理场均匀性前提下, 根据GTF滑动轴承性能要求的优先级, 在鼓型、R型和L型轴向母线滑动轴承中进一步筛选。比如, 考虑到R型母线滑动轴承油膜温度低和油膜厚度大, 其更适应滑动轴承使用寿命长和工作运行可靠性高的要求。

3.2 偏心率和转速对4种轴向母线滑动轴承性能的影响

1) 偏心率的影响

在滑动轴承转速为8 500 r/min、供油温度为27℃的条件下, 图 4对比了偏心率分别为0.75, 0.80, 0.85和0.90时4种轴向母线滑动轴承润滑性能。可以看出, 随着偏心率增加, 最大油膜压力、油膜承载力和最大油膜温度也增加, 而最小油膜厚度则减小。此外, R型轴向母线滑动轴承在最小油膜厚度和最大油膜温度方面具有优势。

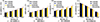thumbnail 图4

不同偏心率下滑动轴承润滑性能对比

2) 轴颈转速的影响

在供油温度为27 ℃、偏心率为0.8的条件下, 图 5对比了转速分别为7 000, 7 500, 8 000, 8 500和9 000 r/min时4种轴向母线滑动轴承润滑性能。可以看出, 随着滑动轴承转速增加, 最大油膜压力、油膜承载力和最大油膜温度均增加, 而最小油膜厚度则略微减小。原因是较大的油膜压力和油膜温度会导致弹性变形和热变形增加, 进而导致轴承间隙降低和油膜厚度减小。此外, R型轴向母线滑动轴承在最小油膜厚度和最大油膜温度方面表现最佳。

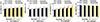thumbnail 图5

不同转速下滑动轴承润滑性能对比

3.3 轴颈倾斜对滑动轴承性能的影响

上述分析表明, R型轴向母线和直线型轴向母线滑动轴承性能差异最大, 需进一步研究轴颈倾斜对2种轴向母线滑动轴承性能及差异的影响。

在转速为8 500 r/min、供油温度为27 ℃、偏心率为0.8的条件下, 图 6对比了不同轴颈倾斜角度对R型轴向母线和直线型轴向母线滑动轴承润滑油膜轴向物理场的影响。可以看出, R型轴向母线滑动轴承的最小油膜厚度、最大油膜压力和最大油膜温度的轴向分布均匀性程度都较高, 而且R型轴向母线滑动轴承润滑油膜轴向物理场的均匀性并没有随着轴颈倾斜角度的增加产生明显变化。此外, 轴颈倾斜使轴端处油膜厚度减小、楔形油膜挤压效应增大, 进而导致油膜最大压力和最高温度位置均向轴端移动。然而, 即使考虑轴颈倾斜, R型轴向母线滑动轴承在轴端处的最高温度仍显著低于直线型轴向母线滑动轴承。

thumbnail 图6

不同轴颈倾斜角度下2种滑动轴承润滑油膜轴向物理场对比

4 面向润滑油膜轴向物理场均匀化的GTF滑动轴承优化设计

以润滑油膜轴向物理场均匀化程度高的R型轴向母线滑动轴承为对象, 以滑动轴承承载力、油膜最大温度和油膜轴向均匀化系数为优化目标, 建立R型轴向母线GTF滑动轴承优化设计模型。该模型使用线性加权法将单目标优化得到的目标函数最优值代入加权因子, 进而嵌入多目标优化函数中, 建立R型轴向母线GTF滑动轴承性能多目标优化模型。模型各加权因子为单目标优化的函数最优值倒数。通过滑动轴承结构参数和修形参数的优化设计, 获得满足润滑油膜轴向物理场均匀性要求、高承载力及低油膜温升的滑动轴承优化结构。

4.1 优化设计模型

在GTF滑动轴承结构和安装空间确定的前提下, 可优化的滑动轴承设计变量仅有半径间隙c和凸度系数k, 分别表示为x1=c和x2=k。将设计变量对应的矩阵表示为X =[x1, x2]。以滑动轴承承载力、油膜最大温度和轴向均匀化系数为优化目标, 构建的GTF滑动轴承优化目标函数。

考虑到轴颈和轴瓦表面粗糙度、弹性变形与热变形、润滑油清洁度及杂质粒度等的影响, 最小油膜厚度hmin需要满足下述条件

式中: n为安全系数, 一般取n=2~3;RZ1, RZ2分别为轴颈和轴瓦的表面粗糙度, 取2.1~3.2 μm, 最小油膜厚度为12 μm。

查询国家标准[17]推荐半径间隙c为0.09 mm, 为了优化方便对半径间隙的取值适当扩大。对于R型轴向母线滑动轴承的凸度取值, 应使R型轴向母线滑动轴承在最大凸度系数下的修正量不超出最小油膜厚度。故设计变量的约束条件为: 半径间隙0.03 mm≤c≤0.15 mm, 凸度系数0≤k≤1.52。

4.2 R型轴向母线滑动轴承的参数优化

1) 油膜承载力、最大温度和轴向均匀化系数的单目标优化

采用遗传算法, 种群数设为200, 最大迭代次数为70, 分别对油膜承载力、最大温度和均匀化系数进行单目标优化求解。对于油膜承载力, 获得油膜承载力单目标优化种群平均适应度为4.613×10-6, 目标函数最优值为4.624×10-6, 此时设计变量值X =[0.03, 0];对于油膜最大温度, 获得最大温度单目标优化种群平均适应度为47.789, 目标函数最优值为47.786, 此时设计变量值X =[0.15, 0.734];对于油膜轴向均匀化系数, 获得油膜轴向均匀化系数单目标优化种群平均适应度为8.355×10-3, 目标函数最优值为8.354×10-3, 此时设计变量值X =[0.126, 0.186]。

2) R型轴向母线滑动轴承参数的多目标优化

将单目标函数优化得到的函数最优值代入到加权因子, 进而得到R型轴向母线GTF滑动轴承性能多目标优化函数。采用遗传算法, 种群数设为200, 最大迭代次数为70, 加入约束条件, 对GTF滑动轴承多目标函数进行优化求解, 获得多目标函数种群平均适应度为2.417, 多目标函数最优值为2.411, 此时设计变量值X =[0.075, 1.52]。

表 3对比了R型轴向母线GTF滑动轴承原始设计参数、单目标优化后设计参数和多目标优化后设计参数的性能。可以看出, 相较于原始参数的GTF滑动轴承, 虽然关于油膜承载力、油膜最大温度和油膜轴向均匀化系数的单目标优化设计都能使各自优化的单目标性能提高, 但不能兼顾其他性能。而通过多目标性能优化, R型轴向母线GTF滑动轴承的油膜承载力虽有所降低, 但其最大油膜温度和轴向油膜的均匀化程度都得到了改善(前者降低了17.13%, 后者减小了74.42%)。

表3

优化设计结果对比

通过多目标优化获得的R型轴向母线GTF滑动轴承的半径间隙为0.075 mm、凸度系数k=1.52。图 7对比了不同轴颈倾斜角度下优化后R型轴向母线GTF滑动轴承的油膜轴向物理场分布。可以看出, 优化后的R型轴向母线GTF滑动轴承轴向油膜厚度、轴向最大油膜压力和轴向最大油膜温度也都随着倾斜角度的增加而有所增大。

thumbnail 图7

计及轴颈倾斜优化后R型轴向物理场分布

表 4对比了优化前后R型轴向母线GTF滑动轴承的轴向物理场均匀化系数和承载力。虽然轴颈倾斜会导致轴向物理场均匀化系数和承载力的增大, 但优化后的滑动轴承轴向物理场均匀化系数和承载能力仍显著优于优化前结果。这表明优化后的滑动轴承不仅承载力和轴向物理场均匀性得到提升, 而且对轴颈倾斜角度变化也具有较好的性能鲁棒性, 这有利于提高GTF滑动轴承运行可靠性。

表4

不同倾斜角度下优化前后结果对比

5 结论

针对航空发动机中GTF滑动轴承在高转速、高比压和大偏心工况下, 易出现轴端局部热变形过大、轴向油膜厚度分布不均、倾斜轴颈碰磨风险增大等问题, 提出了滑动轴承油膜轴向物理场均匀化系数这一设计评价参数, 并据此开展了不同偏心率、转速、轴颈倾斜角度下4种轴颈轴向母线GTF滑动轴承性能分析和对比, 以油膜轴向物理场均匀化系数为优化目标之一, 通过多目标优化获得了综合性能较佳的滑动轴承轴颈轴向母线构型参数, 并对参数优化后的滑动轴承性能进行了分析。相关结论如下:

1) 滑动轴承轴向结构设计对轴承性能有显著影响。相较于直线型, 鼓型、R型和L型滑动轴承的最大油膜压力分别降低了为16.55%, 18.40%和17.74%, 最大油膜温度分别减少了11.80%, 35.96%和30.58%。

2) 在大偏心和轴颈倾斜工况下, R型轴颈轴向母线对滑动轴承润滑性能的改善效果最优, 可显著降低整体油膜温度、平均油膜压力场和温度场, 其油膜压力峰随着轴颈倾斜角度的增加向轴承端部移动, 且靠近同一端处轴向温度梯度增大。

3) 在高转速、高比压和大偏心工况下, 基于油膜轴向物理场均匀化系数优化的GTF滑动轴承的综合性能明显提升, 且在不同倾斜角度条件下的性能稳定性更高, 这对进一步提升滑动轴承运行可靠性具有重要参考价值。

References

  1. RIEGLER C, BICHLMAIER C. The geared turbofan technology-opportunities, challenges and readiness status[C]//1st CEAS European Air and Space Conference, Berlin, 2007: 10–13 [Google Scholar]
  2. LIU Xiaofan, FENG Jin, QIN Kun. Analysis of transmission efficiency of fan drive gearbox of GTF engine[J]. Mechanical Engineering & Automation, 2019(6): 21–23 (in Chinese) [Google Scholar]
  3. MO Shuai, ZHANG Yidu, WU Qiong, et al. Research on load sharing mechanism of star gear trains for GTF engine[J]. Journal of Aerospace Power, 2016, 31(3): 763–768 (in Chinese) [Google Scholar]
  4. ZHANG C, WEI J, WANG F, et al. Dynamic model and load sharing performance of planetary gear system with journal bearing[J]. Mechanism and Machine Theory, 2020, 151: 103898 (in Chinese) [Google Scholar]
  5. BAO Jianqiao, GUO Hong, LI Ruizhen, et al. Thermoelastohydrodynamic lubrication state and characteristics of journal bearing under large eccentricity condition[J]. Lubrication Engineering, 2023, 48(5): 7–15 (in Chinese) [Google Scholar]
  6. XU Haibuo, SHEN Yunwen, ZHU Jun. On taylor vortex flow in infinite-length eccentric cylinders[J]. Journal of Northwestern Polytechnical University, 1995, 13(2): 168–173 (in Chinese) [Google Scholar]
  7. YIN Chunjun. Experimental research on the eccentric taylor-couette flow in small gap[D]. Wuhan: Huazhong University of Science and Technology, 2020 (in Chinese) [Google Scholar]
  8. MOKHTARI N, PELHAM J G, NOWOISKY S, et al. Friction and wear monitoring methods for journal bearings of geared turbofans based on acoustic emission signals and machine learning[J]. Lubricants, 2020, 8(3): 29 [Google Scholar]
  9. WANG Lin, HAN Zhanhai, CHEN Guoding, et al. Thermo-hydrodynamic analysis of large-eccentricity hydrodynamic bearings with texture on journal surface[J]. Journal of Mechanical Engineering Science, 2018, 232(19): 3564–3569 [Google Scholar]
  10. ZHANG Yu, CHEN Guoding, WANG Lin. Thermoelastohydrodynamic analysis of misaligned bearings with texture on journal surface under high-speed and heavy-load conditions[J]. Chinese Journal of Aeronautics, 2019, 32(5): 1331–1342 [Google Scholar]
  11. XIANG G, HAN Y, HE T, et al. Wear and fluid-solid-thermal transient coupled model for journal bearings[J]. Applied Mathematical Modelling, 2020, 8519–45 [Google Scholar]
  12. LI Chunjian, ZHAO Junsheng, ZHU Guixiang, et al. Effect of main bearing-journal profiles on lubrication performance based on whole engine block[J]. Lubrication Engineering, 2021, 46(8): 62–68 (in Chinese) [Google Scholar]
  13. GORASSO L, WANG L. Journal bearing optimization using nonsorted genetic algorithm and artificial bee colony algorithm[J]. Advances in Mechanical Engineering, 2014, 6213548 [Google Scholar]
  14. SILVEIRA A R G, DANIEL G B. Influence of bearing ovalization in the dynamic of a planar slider-crank mechanism[J]. Applied Mathematical Modelling, 2019, 66: 175–194 [Google Scholar]
  15. REUSNER H. The logarithmic roller profile-the key to superior performance of cylindrical and taper roller bearings[J]. Ball Bearing Journal, 1987, 230: 2–10 [Google Scholar]
  16. HE Zhixian, GUI Changlin. A fast approximate algorithm of lubrication analysis for a bearing with elastic bush[J]. Lubrication Engineering, 20075): 48–51 (in Chinese) [Google Scholar]
  17. DING Baoping, XU Hua, QIAN Zhong. Plain bearing hydrodynamic plain journal bearings under steady-state conditions-circular cylindrical bearings-part 3: permissible operational parameters[S]. GB/T 21466.3-2008 (in Chinese) [Google Scholar]

All Tables

表1

滑动轴承结构和工况参数

In the text
表2

不同轴颈母线的滑动轴承润滑性能

In the text
表3

优化设计结果对比

In the text
表4

不同倾斜角度下优化前后结果对比

In the text

All Figures

thumbnail 图1

不同运行状态下的滑动轴承结构示意图
In the text
thumbnail 图2

4种轴颈轴向母线函数方程及构型示意图
In the text
thumbnail 图3

4种轴向母线滑动轴承的润滑油膜轴向物理场
In the text
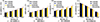thumbnail 图4

不同偏心率下滑动轴承润滑性能对比
In the text
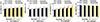thumbnail 图5

不同转速下滑动轴承润滑性能对比
In the text
thumbnail 图6

不同轴颈倾斜角度下2种滑动轴承润滑油膜轴向物理场对比
In the text
thumbnail 图7

计及轴颈倾斜优化后R型轴向物理场分布
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.