EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 2 (April 2025) JNWPU, 43 2 (2025) 222-232 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 2, April 2025
Page(s) 222 - 232
DOI https://doi.org/10.1051/jnwpu/20254320222
Published online 04 June 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

导航卫星是全球卫星导航系统不可或缺的组成部分, 星座可用性是其系统可靠性与可维护性的综合体现, 与星座备份策略、补充替换方案、地面控制等因素密切相关[1–3]。通过冗余配置设计，防止星座因工作卫星发生故障而无法满足性能要求, 这是确保卫星星座运行稳定的关键因素[4]。从星座备份策略的角度对星座的可用性进行研究极具意义。

目前, 国内外很多机构和学者对卫星星座的备份策略和可用性进行了研究。Ereau等[5]使用了随机时间Petri网以进行星座模型定量分析。王许煜等[6]利用随机时间Petri网建立了星座运行状态变化模型, 以星座可用性作为评价指标之一研究星座的备份策略, 然而在考虑在轨备份卫星的补充方式时, 只研究了当某条轨道面内的在轨备份卫星耗尽时才将其补充至原有水平的情况, 并且未对星座的备份策略和可用性建立明确的数学模型。侯洪涛等[7]根据马尔可夫过程, 利用分系统的部件失效提出了单星可用度算法, 基于星座的状态概率建立了导航星座服务可用性计算模型。然而在模型中并未详细考虑星座的备份策略, 仅仅是使用维修率作为代表。王尔申等[8]同时考虑卫星故障率和修复率, 并结合卫星的在轨备份情况, 基于马尔可夫过程建立了星座可用性评估方法模型, 然而其备份策略并未考虑备份卫星在地面备份的情况, 也未对在轨备份卫星的补充方式进行探讨。Valdez-Flores等[9]利用离散时间马尔可夫链进行星座建模, 并做了诸如不考虑发射提前准备时间等假设以解决星座状态空间爆炸的问题, 接着利用马尔可夫决策过程进行随机动态规划以确定最优替换策略, 但是其星座备份策略只考虑了地面备份的情况。Kelley等[10]也使用马尔可夫链模型计算星座的覆盖可用性, 结合备份策略的相关成本评估星座系统的寿命周期成本, 并使用模拟退火算法和遗传算法进行优化, 但是并未分析备份策略是如何影响星座可用性的, 对于备份卫星的部署位置也只考虑了在轨备份。Peng等[11]考虑了在轨以及地面备份卫星, 在单星马尔可夫链模型的基础上, 使用了概率模型检查工具PRISM[12], 对单星以及星座可用性进行了分析, 不过其并未分析备份策略对星座可用性的影响。上述文献在进行星座建模时主要关注星座状态的随机变化, 星座的备份策略并非建模重点。也有学者基于库存管理理论, 通过星座的备份策略对星座可用性进行分析。Dishon等[13]通过(N, M)库存系统对星座的状态变化进行建模, 以求解卫星补给问题。Jakob等[14]采用多级(s, Q)库存策略, 同时考虑系统中不同级别的备份卫星, 将星座的保障系统视为一个多层次的备份供应链。骆天溯等[15]基于多级库存管理论(multi-echelon technique for recoverable item control, METRIC)提出一种超大规模卫星星座多级备份策略。同时考虑地面备份、停泊轨道及星座轨道备份3种备份模式, 建立星座可用度模型和以星座可用度为约束, 最低星座备份费用为优化目标的优化模型。上述文献虽然着重考虑了备份策略对星座可用性的影响, 但是在计算可用性时直接将备份卫星能满足替换需求的概率作为星座可用性, 结果相对静态, 无法反映星座在不同故障卫星颗数下的可用性, 且忽视了卫星在轨短期故障与短期修复的过程。然而在实际工程中, 卫星被设计为冗余备份的形式, 具有应对短期故障的准备(硬件冗余、地面重启等), 不考虑短期故障在工程应用中是一种资源浪费。本文对短期故障的考虑能进一步降低应用成本, 保证系统功能最大化利用。

本文在上述研究成果及相应问题的基础上, 考虑导航卫星星座备份策略、故障卫星颗数、短期故障和长期故障及修复, 提出一种基于多级库存管理理论的星座可用性研究方法。通过分析星座备份策略的组成要素以及备份策略与卫星长期故障修复率的关系, 以备份卫星的保障率为指标建立星座备份策略的数学模型, 并集成应用Petri网、马尔可夫链理论, 建立星座服务可用性的数学模型。该方法克服了多级库存管理理论只提及静态星座服务可用性、马尔可夫法未考虑星座备份策略的问题, 并将短期故障纳入考虑范围。此外, 本文以具体案例探讨了不同备份卫星部署位置及其补充方式对星座可用性的影响, 进一步完善了备份策略的优化模型, 从而能够更细致全面地研究星座备份策略对星座服务可用性的影响。

1 星座的备份策略模型

1.1 备份策略概述

星座的备份策略可以归结出3个要素: ①备份卫星的部署位置; ②使用与补充备份卫星的方式; ③备份卫星的部署数量。

为了简化建模过程, 提高工程适用性, 对卫星星座采取以下假设:

1) 星座中卫星的失效次数服从泊松分布[16]；

2) 处于备份状态的卫星不会发生失效, 不考虑卫星工作期间共因失效的情况。

1.2 备份卫星的部署场所

星座的备份策略通常包括3种模式: 在轨备份、停泊轨道备份以及地面备份, 前2种统称为空间备份[17]。从这个角度出发, 根据星座部署备份卫星的位置, 可以划分出2种备份层级: 空间备份层级和地面备份层级。各备份层级中备份卫星的部署场所及特点如表 1所示。

表1

各备份层级中备份卫星的部署场所及特点

1.3 使用与补充备份卫星的方式

使用备份卫星的方式分为2种:

1) 替换故障卫星: 因工作卫星故障产生替换的需求时, 就启用备份卫星进行替换；

2) 补充其他部署场所消耗的备份卫星: 部署在地面备份层级的备份卫星可以用于补充空间备份层级的备份卫星。

对消耗的备份卫星进行补充的方式也有2种:

1) 使用其他部署场所的备份卫星进行补充；

2) 生产新的备份卫星进行补充。

当明确补充备份卫星的方式时, 还需确定备份卫星数量的控制策略, 即考虑进行补充的时机以及需要补充的备份卫星颗数。备份卫星的数量控制策略用(R, Q)来描述, 即当某一部署位置上的备份卫星颗数降至R时, 就调配其他部署位置的Q颗备份卫星或生产Q颗备份卫星进行补充。

1.4 备份卫星的部署数量

在整个星座的服役时期中, 部署于轨道或仓库中的备份卫星的数量并不是一个定值, 而是会随着使用与补给而发生变化。用预定的备份卫星目标数量S与一段时期内备份卫星的平均数量S来衡量某个轨道或仓库中备份卫星的部署数量的水平。

式中: N(t)为在t时间内星座需要替换的故障卫星数量; t为补充该场所备份卫星的耗时。

1.5 星座备份策略的评价指标

本文将各部署场所的备份卫星保障率作为星座备份策略的评价指标。备份卫星保障率指当星座产生备份卫星的使用需求时, 某一部署场所上的备份卫星数量能够满足该需求的概率。为了计算备份卫星的保障率, 需要计算2个中间量: 备份卫星的平均需求量以及期望短缺颗数。

各部署场所的备份卫星平均需求量m与备份卫星所处的备份层级有关, 如(2)式所示。

式中: m0为星座的年平均备份卫星需求量; P为备份层级的备份卫星部署场所数量, 对于空间备份层级, 其为星座工作轨道数或停泊轨道数; 对于地面备份层级, 其为贮存备份卫星的仓库数。

星座的年平均备份卫星需求量计算公式为

式中: Ty为星座在每年内的运行时间; Pc为星座工作轨道数量; nc为第c个星座工作轨道上的工作卫星数量; tL为工作卫星发生长期故障的平均故障间隔时间。

当备份卫星部署场所i产生使用备份卫星的需求时, 若具有的备份卫星数量少于需求数量, 就会发生短缺现象。假设备份卫星需求量为NDI且服从均值为μi的泊松分布, 在该备份场所的备份卫星平均数量为Si的情况下, 期望短缺数EBO(Si)计算公式为

μi是备份卫星的部署场所在等待从其他部署场所补充备份卫星时的备份卫星期望需求量, 由该时期内的备份卫星使用需求和因后方补给不及时而造成的短缺两部分组成。μi计算公式为

式中: mi为备份场所i的年平均备份卫星需求量; tj, i是补给用备份卫星的备份场所j向备份场所i补充备份卫星的耗时; mj为备份场所j的年平均备份卫星需求量; EBO(Sj)为备份场所j的期望短缺数; m0是星座的年平均备份卫星需求量。

对于部署场所i而言, 当贮存在该处的备份卫星用于替换故障卫星时, 其备份卫星保障率Pi为

式中: Pc为星座工作轨道数量; nc为第c个星座工作轨道上的工作卫星数量。

当贮存在该处的备份卫星用于补充其他部署场所h的备份卫星时, 其备份卫星保障率Pi, h为

式中: Ph为部署场所h所在的备份层级轨道数; nh为第h个备份层级轨道上的备份卫星数量。

2 星座可用性

2.1 单星可用性模型

卫星的在轨故障模式可以分为短期和长期故障[18]。短期故障可以通过地面发出重启指令或切换备件等手段修复, 耗时较短; 长期故障则需要启用备份卫星进行替换, 这需要较长的时间。假设卫星的长期故障和短期故障的平均故障间隔时间以及平均修复间隔时间都服从指数分布[19–20], 根据可靠性理论[21–22], 在轨工作卫星稳态可用度为

式中: λtotal为在轨工作卫星故障率; μtotal为在轨工作卫星修复率。

λtotal和μtotal受卫星在轨期间会发生的故障模式及对应的修复方式影响。在轨工作卫星的故障率λtotal的计算公式为

式中: λL为在轨工作卫星发生长期故障的故障率; λS为在轨工作卫星发生短期故障的故障率。

在轨工作卫星的总修复率μtotal为

式中: μS为在轨工作卫星发生短期故障的修复率; μL为在轨工作卫星发生长期故障的修复率。

单星的长期非计划故障一般难以预见, 长期非计划故障的时间取决于在轨备份、停泊轨道备份、按需发射备份等不同星座备份策略, 需要依靠启用备份卫星替换解决。然而长期非计划故障难以预见, 因此在发生长期非计划故障时, 若是星座没有采用在轨备份的策略或者说在轨备份卫星还未得到补给, 那么就需要等待一段时间。Petri网可以详细地表达系统中的运行逻辑, 反映系统的静态布局以及动态变化, 传统的Petri网只研究当某条轨道面内的在轨备份卫星耗尽时才将其补充至原有水平, 本文所采用的随机Petri网模型中, 变迁时间假设服从指数分布, 使用Petri网建立卫星发生长期故障并启用备份卫星替换的流程模型如图 1所示, 其中圆圈表示库所, 短线表示变迁, 有向弧表示关系, 圆点表示标记[23–24]。

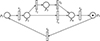thumbnail 图1

替换故障卫星的Petri网模型

图 1中各库所的意义如表 2所示。结合图 1可知, 当工作卫星发生长期故障, 需要启用备份卫星进行替换时, 若是备份卫星的部署场所中卫星数量不足, 则需要等待补充完毕后才能进行替换。

卫星长期故障的故障率可用(11)式表示

式中: λL为卫星发生长期故障的故障率; T6为长期计划中断的平均故障间隔时间。

卫星的长期故障修复率可用(12)式表示。

式中: μL为卫星长期计划故障中断的修复率; T1为平均排故耗时, 是发现卫星发生长期故障的时间; f为备份卫星不足的概率; T3为补充备份卫星平均耗时; T4是卫星长期故障的平均修复时间, 可以认为是由备份卫星启用到开始承担故障卫星任务所需的时间。

当工作卫星发生长期故障, 使用部署场所i的备份卫星进行替换, 则备份卫星不足的概率f为

式中, Pi为部署场所i的备份卫星保障率。

表2

替换故障卫星的Petri网符号意义

2.2 星座的状态概率

若星座具有N颗工作卫星, 在某时刻t, 每颗工作卫星均有正常和故障2种状态, 这2种状态可视为此随机过程的未来状态条件概率分布只依赖于当前的状态, 而不依赖于这之前的状态, 根据马尔可夫链的定义, 可认为这个随机过程具有马尔可夫性质。根据星座中故障卫星的颗数区分星座的状态, 从无卫星故障到N颗卫星故障共会有N+1种状态[8]。

用λi表示星座在有i-1颗卫星发生故障状态下的故障率, Δt表示状态转移时间间隔。

式中, λ为N颗工作卫星的平均故障率。

用μj表示星座在有j颗卫星发生故障的状态下的修复率, 其计算公式为

式中, μ为N颗工作卫星的平均修复率。

令Gn(t0+kΔt)表示t0+kΔt时刻星座处于有n颗卫星发生故障的状态的概率，n=0, 1, …, N。那么在不同的时间点, 星座处于不同状态的概率向量为

式中

定义当k=0时, G (t0)表示卫星星座初始时刻状态概率向量, 如(20)式所示。

式中, A表示卫星单星可用度。

2.3 星座的服务可用性

利用星座的服务可用性衡量导航星座的可用性。星座的服务可用性定义为在一段时间内, 系统提供的卫星业务服务满足用户需求的时间百分比, 通过星座的状态概率以及星座值计算。星座值是星座的固有特性, 反映了星座在某种状态下满足规定性能要求的能力。对于导航星座, 可以指覆盖区内位置精度衰减因子(position dilution of precision, PDOP)小于阈值的区域占整个服务区的面积的百分比在全时段上的平均值[25], 计算公式为

式中: kΔt为星座总运行时间; t0为初始时刻; L为格网点总个数; B(x)为布尔函数, 当x为真时, B(x)=1, 当x为假时, B(x)=0;βPDOP, t, i为第i个格网点在t时刻的PDOP值; At为服务区域总面积; Ai为第i个格网点的面积。

星座的服务可用性计算公式如下

式中: As为星座服务可用性; N为星座中的工作卫星总数。

采用基于多级库存管理理论的导航星座可用性计算流程如图 2所示。

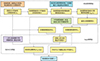thumbnail 图2

星座服务可用性建立流程图

3 案例分析

3.1 案例星座参数

Walker星座是由英国航天院的John Walker提出的一种由等高度和等倾角的同构圆轨道组成的倾斜对称圆轨道卫星星座[26], 某Walker导航星座构型及平均故障间隔时间如表 3所示。

以全球为服务区域, 网格划分为5°×5°, 最小观测仰角为5°, 指标要求为βPDOP≤4, 计算时间取一个星座回归周期, 步长300 s。表 4给出了星座在无故障卫星直至有3颗卫星发生故障的情况下, 星座值的最大值与最小值。

当出现星座故障卫星达到4颗及以上的状态时, 认为星座服务不可用, 此时星座值取为0。

表3

导航星座案例输入

表4

不同故障卫星数下的星座值

3.2 星座状态概率

案例星座中可能出现的故障卫星颗数为0~8, 将各星座轨道划分为9种状态, 即星座的起始状态为“无故障卫星”。根据2.2节基于马尔科夫链计算星座状态概率的方法, 以时间步长Δt=1 h、总运行时长5年作约束, 仿真得到星座轨道处于这9种状态的概率, 其中前4种状态概率结果如表 5所示。

以整个星座处于无故障卫星、1颗故障卫星和2颗故障卫星的状态为例, 该状态概率随着时间的变化如图 3~4所示。

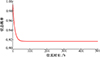thumbnail 图3

星座无故障卫星状态概率变化示意图

thumbnail 图4

星座存在卫星故障状态概率变化示意图

随着时间增加, 星座处于无故障卫星状态的概率逐渐下降, 直到50 h后才逐渐趋于平稳, 而处于有1颗故障卫星以及2颗故障卫星状态的概率逐渐上升，这意味着星座中卫星故障逐渐发生, 在前50 h星座处于有1颗故障卫星状态概率的上升趋势更加显著, 50 h后处于1颗故障卫星和2颗故障卫星状态概率逐渐趋于平稳。根据上述结果可以发现, 导航星座在运行中处于无故障卫星状态的概率并不高, 这也表明了分析星座状态概率, 并将其融入衡量星座可用性量化值的必要性。

表5

运行5年后星座的状态概率

3.3 备份策略分析

3.3.1 地面备份卫星颗数影响

若是星座不采取备份策略, 仅在地面备份卫星, 即当在轨工作卫星发生长期故障后, 就由地面生产卫星然后进行发射替换, 对于使用地面与停泊轨道备份的2级备份策略执行模式和仅采用地面备份的单级备份策略执行模式, 在其他备份层级的备份卫星订购点和每次的补充数量为1颗的情况下, 地面备份卫星数量对星座服务可用度及星座保障率的影响如图 5所示。

thumbnail 图5

地面备份卫星数量对2级备份和单级备份的星座服务可用度及星座保障率影响

对于单级设备策略，仅在地面备份1颗卫星, 服务可用度和星座保障率分别为0.269 7和0.137 2, 而采取2级备份策略后, 仅在地面备份1颗卫星, 星座的服务可用性也会上升为0.855 9, 星座保障率上升为0.933 2, 与单级备份策略相比分别上升了217.35%和580.17%, 可见采取2级备份策略对星座服务可用性和保障率的提升显著。

使用地面与停泊轨道备份的2级备份策略执行模式的星座比单级备份策略执行模式具有更多的备份卫星, 因此起初服务可用度较高。并且替换故障卫星时, 一个需要等待备份卫星漂移和变轨, 一个需要地面准备和发射, 所以一开始地面备份卫星数量的增加对结果影响并不显著, 随着地面备份卫星颗数的增加, 单级备份服务可用度呈显著上升趋势, 在地面备份卫星颗数达到4颗时, 其服务可用度超过了使用地面与停泊轨道备份的情况, 之后两者服务可用度的变化都趋于平缓, 单级备份策略的更高, 这是由于对于地面备份卫星而言, 在单级备份情况下可以直接用于替换故障卫星, 而在2级备份的情况下还需先储存在停泊轨道上, 耗时更长。

不论是单级备份还是2级备份, 星座服务可用度均在数值上对比星座保障率有较大提升, 说明仅采取库存管理理论对保障导航星座可用性是远远不够的。

3.3.2 申请补给的备份卫星颗数影响

针对本文中使用地面备份与在轨备份的2级备份模式, 改变星座轨道每次申请补给的备份卫星颗数Qo以研究该变量对计算结果的影响。在订购点Ro=1和地面备份卫星数量为0的情况下, 不同Qo值下的计算结果如图 6所示。

thumbnail 图6

Qo值的变化对计算结果的影响

由图 6可以看出, 随着星座轨道每次申请补给的备份卫星数Qo增加, 星座服务可用性以及在轨备份卫星的保障率均上升。Qo对备份卫星保障率的影响比对服务可用性的影响更为显著。当其数量从2颗增长至3颗时, 星座服务可用性和备份卫星保障率的增幅最大, 分别为5.96%和52.46%, 之后服务可用性增幅放缓, 最终稳定至近0.95, 备份卫星保障率从4颗开始再次产生较大增幅, 最终稳定至近1, 说明备份卫星每次补充颗数与在轨工作卫星颗数已接近。

3.3.3 星座轨道订购点影响

改变星座轨道备份卫星的订购点Ro以研究该变量对计算结果的影响。在每次补给的在轨备份卫星数Qo=1和地面备份卫星数量为0的情况下, 不同Ro值下的计算结果如图 7所示。

thumbnail 图7

Ro值的变化对2级备份计算结果的影响

随着星座轨道备份卫星订购点Ro的增加, 星座服务可用性以及在轨备份卫星的保障率均上升。从1颗增至2颗和2颗增至3颗过程中, 备份卫星保障率增幅显著, 分别为52.46%和13.21%, 之后增幅放缓; 服务可用性在2颗增至3颗过程中增幅较为显著(为4.65%)。由于Ro表征的是某一星座轨道上备份卫星的最少颗数, 因此相比于同一备份层级的另一参数Qo, 增加Ro星座的服务可用性和备份卫星的保障率增长更加迅速。

3.4 故障影响分析

根据前文分析, 采取备份策略能有效提高星座可用度, 针对单个导航卫星的可用性, 传统文献往往只考虑卫星的长期故障, 而忽视卫星存在的短期故障, 但在实际工程中, 卫星被设计为冗余备份的形式, 具有应对短期故障的准备, 例如硬件冗余、地面重启等, 若不考虑短期故障, 在工程应用中是一种浪费。长期故障可采用延长单元寿命进行改善, 而通过加强单粒子设计、电磁兼容设计、静电防护设计等措施, 可有效提升短期故障平均故障间隔时间[27]。根据备份策略分析结果, 选择同时采用地面备份与在轨备份策略并选取地面备份4颗卫星的较优方案, Ro=2, Qo=4的轨道备份卫星数量控制策略, 分别对长期故障平均故障间隔和短期故障平均故障间隔按一定比例进行提升优化, 将所得星座服务可用性结果进行对比, 如图 8所示。

thumbnail 图8

平均故障间隔提升对比

随着平均故障间隔提升比例的提高, 在20%前, 长期故障对星座服务可用性的影响略高于短期故障, 且两者的方差逐渐减小, 在提升比例达到20%~25%之间后, 短期故障对星座服务可用性的影响开始高于长期故障。由此可见短期故障对星座服务可用性的影响与长期故障相差无几, 甚至在优化一定程度后优于长期故障, 短期故障在实际计算星座服务可用性中是不可忽视的。在实际星座设计中, 应根据短期故障和长期故障的不同特点, 分别制定相应的优化策略, 进一步提升星座的整体可用性和效能。

4 结论

本文基于库存管理理论建立了星座备份策略的分析模型, 结合Petri网和马尔可夫理论提出了星座备份策略的评价指标以及根据该指标计算星座服务可用性的方法, 克服了传统单一方法只提及静态服务可用性、忽视短期故障的问题, 更加符合工程实际, 进一步降低应用成本, 最后使用所提方法对案例导航星座进行研究验证, 得出以下结论:

1) 实际导航星座在运行中处于无故障卫星状态的概率并不高, 仅采用马尔可夫理论而不考虑备份策略分析星座可用性具有局限性。

2) 库存管理理论能够解决星座备份策略不够细致的问题, 而仅采取库存管理理论的备份策略具有服务可用性静态且忽视短期故障的局限性, 利用马尔可夫理论分析星座状态概率并将其融入衡量星座可用性的量化值具有重要意义。

3) 采用基于多级库存管理理论的2级备份策略相比于单级备份策略在星座服务可用性的提升上效果显著。在相同的备份卫星数量下, 比起仅在地面备份, 采用将备份卫星部署在地面和星座工作轨道上的2级备份策略对星座的服务可用性具有较大提升。使用备份卫星后, 增加地面备份卫星的数量、提前补充备份卫星的时机、增加备份卫星每次补充颗数对星座的服务可用性提升效果有限, 实际应用中应根据成本灵活选择最优策略。提升短期故障平均故障间隔与提升长期故障平均故障间隔对提高星座服务可用性的效果近似, 短期故障在工程应用中同样不可忽略。

4) 所提方法在应对复杂或高度随机的故障模式时, Petri网和马尔可夫法可能存在局限性。此外, 结果对输入数据的依赖性较强, 实际应用中可能会因数据偏差影响准确性。未来研究应探索提高模型的扩展性和计算效率, 并结合实际数据和先进算法实现备份策略的精确优化和系统效能的全面提升。

References

  1. HU Zhigang. Beidou navigation satellite system performance assessment theory and experimental verification[D]. Wuhan: Wuhan University, 2013 (in Chinese) [Google Scholar]
  2. ZHANG Qinghua, WANG Yuan, SUN Yangyang, et al. Initial assessment of signal-in-space availability for BDS[J]. Journal of Geomatics, 2015, 40(6): 22–24 (in Chineses [Google Scholar]
  3. LU Y, PENG Z G, ALICEA M, et al. How reliable is satellite navigation for aviation checking availability properties with probabilistic verification[J]. Reliability Engineering and System Safety, 2015, 144(12): 95–116 [Google Scholar]
  4. HOU Hongtao. Multi-hiberarchy based availbility analysis method for global navigation satellite system[D]. Changsha: National University of Defense Technology, 2015 (in Chinese) [Google Scholar]
  5. EREAU J F, SALEMAN M. Modeling and simulation of a satellite constellation based on Petri nets[C]//International Symposium on Reliability and Maintain Ability Symposium, 1996: 66-72 [Google Scholar]
  6. WANG Xuyu, HU Min, ZHANG Xueyang, et al. Analysis and evaluation method of navigation satellite constellation backup strategy based on Petri net[J]. Systems Engineering and Flectronics, 2021, 43(2): 434–442 (in Chinese) [Google Scholar]
  7. HOU Hongtao, XIE Fei, ZHANG Wangxun, et al. Availability analysis for constellation of GNSS based on Markov process[J]. Systems Engineering and Flectronics, 2014, 36(4): 685–690 (in Chinese) [Google Scholar]
  8. WANG Ershen, ZHANG Qing, QU Pingping, et al. GNSS constellation availability evaluation method based on Markov chain[J]. Systems Engineering and Flectronics, 2017, 39(4): 814–820 (in Chinese) [Google Scholar]
  9. VALDEZ-FLORES C, FELDMAN R M. A survey of preventive maintenance models for stochastically deteriorating single-unit system[J]. Naval Research Logistics, 1989, 36(4): 419–446 [Article] [Google Scholar]
  10. KELLEY C, DESSOUKY M. Minimizing the cost of availability of coverage from a constellation of satellites: evaluation of optimization methods[J]. Systems Engineering, 2004, 7(2): 113–122 [Article] [Google Scholar]
  11. PENG Z, LU Y, MILLER A, et al. Formal specification and quantitative analysis of a constellation of navigation satellites[J]. Quality and Reliability Engineering International, 2016, 32(2): 345–361 [Article] [Google Scholar]
  12. KWIATKOWSKA M, NORMAN G, PARKER D. PRISM: probabilistic model checking for performance and reliability analysis[J]. ACM SIGMETRICS Performance Evaluation Review, 2009, 36(4): 40–45 [Article] [Google Scholar]
  13. DISHON M, WEISS G H. A communications satellite replenishment policy[J]. Technometrics, 1966, 8(3): 399–409 [Article] [Google Scholar]
  14. JAKOB P C M, SHIMIZU S, YOSHIKAWA S, et al. Optimal satellite constellation spare strategy using multi-echelon inventory control[J]. Journal of Spacecraft and Rockets, 2019, 56(5): 1449–1461 [Article] [Google Scholar]
  15. LUO Tiansu, ZHAO Lingfeng, FENG Yunwen, et al. Super large-scale satellite constellation multi-level backup strategybased on METRIC theory[J]. Systems Engineering and Flectronics, 2022, 44(7): 2181–2190 (in Chinese) [Google Scholar]
  16. COLLOPY P. Assigning value to reliability in satellite constellations[C]//AIAA Space 2003 Conference & Exposition, 2003 [Google Scholar]
  17. ZHANG Yulin, FAN Li, ZHANG Yan, et al. Satellite constellation theory and design[M]. Beijing: Science Press, 2008: 180–187 (in Chinese) [Google Scholar]
  18. LIU Jiaxing, CUI Xiaozhun, DONG Haiqing, et al. A backup method for navigation constellation satellites: CN, 201110337755.7[P]. 2023-07-02 (in Chinese) [Google Scholar]
  19. KELLEY C W. GPS constellation state probabilities, historical and projected[C]//Proceedings of the 1999 National Technical Meeting of the Institute of Navigation, San Diego, 1999: 265-270 [Google Scholar]
  20. OCHIENG W Y, SHERIDAN K F, SAUER K, et al. An assessment of the RAIM performance of a combined Galileo/GPS navigation system using the marginally detectable errors(MDE) algorithm[J]. GPS Solutions, 2002, 5(3): 42–51 [Article] [Google Scholar]
  21. CAO Jinhua, CHENG Kan. Introduction to mathematical reliability[M]. Beijing: Higher Education Press, 2012: 182–222 (in Chinese) [Google Scholar]
  22. SONIA M, NIKOLAOS L, PIERRE D. Reliability of maintained systems under a semi-Markov setting[J]. Reliability Engineering and System Safety, 2014, 131(3): 282–290 [Google Scholar]
  23. HU Min, SONG Xumin, YANG Xuerong. Research on spare strategy of Walker navigation constellation based on Petri net[J]. Spacecraft Engineering, 2017, 26(2): 14–21 (in Chinese) [Google Scholar]
  24. LU Weiming, LIN Chuang. Petri net model of production system[J]. Acta Automatica Sinica, 19933): 290–299 (in Chinese) [Google Scholar]
  25. CAI Hongliang, LI Xing. Weakness analysis of navigation constellation based onservice availability[C]//Proceedings of the 5th China Sateuite Novigation Conference, 2014 (in Chinese) [Google Scholar]
  26. WALKER J G. Satellite constellations[J]. Journal of British Interplanetary Society, 1984, 37559–571 [Google Scholar]
  27. YANG Zhuopeng, ZHENG Heng, JIAO Shuyuan, et al. A system effectiveness modeling and analysis method of single navigation satellite[J]. Journal of Astronautics, 2017, 38(6): 647–654 (in Chinese) [Google Scholar]

All Tables

表1

各备份层级中备份卫星的部署场所及特点

In the text
表2

替换故障卫星的Petri网符号意义

In the text
表3

导航星座案例输入

In the text
表4

不同故障卫星数下的星座值

In the text
表5

运行5年后星座的状态概率

In the text

All Figures

thumbnail 图1

替换故障卫星的Petri网模型
In the text
thumbnail 图2

星座服务可用性建立流程图
In the text
thumbnail 图3

星座无故障卫星状态概率变化示意图
In the text
thumbnail 图4

星座存在卫星故障状态概率变化示意图
In the text
thumbnail 图5

地面备份卫星数量对2级备份和单级备份的星座服务可用度及星座保障率影响
In the text
thumbnail 图6

Qo值的变化对计算结果的影响
In the text
thumbnail 图7

Ro值的变化对2级备份计算结果的影响
In the text
thumbnail 图8

平均故障间隔提升对比
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.