A network topology method for cluster communication based on wolf pack algorithm

Xuesi LI; Zheping WU; Haobin SHI; Qingbing JI

doi:10.1051/jnwpu/20254320381

All issues

Volume 43 / No 2 (April 2025)

JNWPU, 43 2 (2025) 381-387

Full HTML

Open Access

Issue		JNWPU Volume 43, Number 2, April 2025


Page(s)		381 - 387
DOI		https://doi.org/10.1051/jnwpu/20254320381
Published online		04 June 2025

JNWPU 2025, 43(2): 381–387

A network topology method for cluster communication based on wolf pack algorithm

一种基于狼群算法的集群通信自组织拓扑方法

Xuesi LI (李学思)¹, Zheping WU (吴哲平)¹, Haobin SHI (史豪斌)¹ and Qingbing JI (吉庆兵)²^,3

¹ School of Computer Science, Northwestern Polytechnical University, Xi'an 710072, China
² National Key Laboratory of Security Communication, Chengdu 610041, China
³ School of Cybersecurity, Northwestern Polytechnical University, Xi'an 710072, China

Received: 13 April 2024

Abstract

The foundation of collaborative control of UAVs is to have a stable and reliable network communication environment, which depends on a high real-time and practical network topology method. This paper proposes a self-organizing topology method for cluster network communication based on wolf pack algorithm (NTM-WPA). Firstly, taking into account constraints such as the location of the UAVs and the load operation state of the UAVs, a multi constraint fusion equivalent distance is proposed. Secondly, the improved wolf pack algorithm is utilized to dynamically search for the shortest network communication path in the equivalent bidirectional communication connection diagram. Finally, the simulation analysis and experiment are designed and conducted, the results demonstrated that the proposed method has better real-time performance and practicality.

摘要

无人机集群协同控制的基础是具备稳定可靠的网络通信环境, 需要设计出高实时、实用化的网络拓扑方法。据此提出了一种基于狼群算法的集群通信自组织拓扑方法。综合考虑无人机集群位置情况、无人机通信载荷运转情况等因素, 提出多约束条件融合的等效距离概念及其计算方法; 利用改进狼群算法在双向通信等效距离连接图中动态搜索最短网络通信路径; 设计相应的仿真和实物测试, 实验结果证明所提方法在实时性、实用性等方面具有更好的结果。

Key words: UAVs / network topology / equivalent distance / wolf pack algorithm

关键字 : 无人机集群 / 网络拓扑 / 等效距离 / 狼群算法

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

随着无人机(unmanned aerial vehicle, UAV)技术的飞速发展, 其应用范围已经涉及民用、商业、科研乃至军事等多个领域[1–2]。基于多架无人机协同的集群系统能够适应更多复杂场景, 为无人机应用产业发展带来了更强劲的动力[3–4]。然而, 无人机集群系统协同控制的核心是建立高效、稳定和满足使用的通信网络, 在此基础上无人机相互之间进行数据交互共享, 获得全局态势信息, 支撑智能化协同决策。

随着通信技术的不断进步和自组织网络概念的日益成熟, 无人机集群组网通信的研究倍受关注。如何在动态、复杂的环境中实现集群无人机之间的智能通信、数据共享和协同决策, 成为当前研究的热点之一。针对此问题, 不少科学家已经做出了许多贡献。文献[5–6]提出基于预先设定的固定网络拓扑方法, 根据专家经验进行固定队形、固定角色和固定层级形式的网络拓扑。该方法允许在系统设计阶段精确规划网络结构, 确保网络满足特定任务需求和约束条件, 提高了通信效率, 简化了系统管理成本。但固定网络拓扑通常较为刚性, 难以适应复杂变化的环境和动态的任务需求, 缺乏灵活性。文献[7–8]提出了基于模糊模式识别和决策系统的机会主义社交网络自适应路由转发控制方法, 通过基于模糊路由分配的网络拓扑方式, 可以实现网络的动态接入和退出, 在一定程度上适应弱连接环境下的节点失效异常工况, 提升整个网络系统的抗毁伤效果, 但考虑到模糊规则设定存在一定主观因素, 将导致系统的灵活性和复杂场景适应性略有不足, 需要围绕动态规划和最优选择开展针对性的算法设计。文献[9–10]提出了基于弗洛伊德算法的拓扑方法, 文献[11–12]提出了基于迪杰斯特拉算法的拓扑方法, 其本质都隶属于动态集群自组织拓扑方法, 利用优化算法进行最优路径搜索, 可以实现集群通信网络的动态拓扑, 提高了网络拓扑的灵活性和弹性。但上述方法规划寻优过程多是以单一因素为考虑, 例如仅考虑通信距离, 但物理网络通信中还需要考虑通信载荷的工作状态、带宽、通信优先级等约束条件, 否则动态规划出的理论拓扑可能会存在与实际使用不匹配的问题。

针对上述无人机集群通信网络拓扑方法中的不足, 本文充分考虑物理通信网络多约束情况, 提出多约束条件融合的等效距离概念, 并在此基础上利用狼群算法[13–14]进行通信网络图动态搜索, 实现贴合物理实际的集群通信网络高效自组织拓扑方法(network topology method based on wolf pack algori-thm, NTM-WPA)。

1 基于等效距离的自组织拓扑方法

当前集群通信网络拓扑多是基于物理距离, 也就是把无人机等效成为三维坐标系中的坐标点, 根据无人机之间的坐标点以及距离公式计算出它们之间的物理距离, 距离越近越容易被选作通信中继节点。然而, 实际物理环境和通信载荷下, 无人机之间的距离、直接通信质量、通信载荷负载率都需要进行考虑, 仅仅采用物理距离来规划网络拓扑结构, 可能无法得出高效率的通信网络。据此, 本文综合考虑节点距离、通信质量(丢包率、延迟)和通信载荷负载率等因素，提出等效通信距离概念, 构建带有无人机集群等效通信距离权重的连接图, 并基于连接图推算某无人机节点至另外一个无人机节点的最优通信多跳链路。

1.1 等效通信距离

如图 1a)所示, 无人机A, B, C, D, E共同组成如图 1b)所示的拓扑结构。如果按照传统方式的物理距离计算, 假设BD之间的距离小于BC与CD之间的距离和, 则从无人机A到无人机E传输信息采用路径A-B-D-E。但在实际环境中, 假设BD之间存在信号干扰因素，则BD之间信息丢包率较高, 传输效率较差, 反而采用路径A-B-C-D-E的方式能够使信息传输更快更有效。据此, 本文引入等效通信距离的概念, 无人机节点i到节点j的等效距离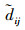计算过程如(1) 式所示。

式中：(x_i, y_i, z_i)和(x_j, y_j, z_j)分别为无人机节点i和j的三维坐标; e_ij表示节点i向节点j发送数据的丢包率, 且e_ij∈[0, 1);C是环境损耗指标常数; t_ij^del为节点i向节点j发送数据的延迟时间; v_ij为节点i和节点j的相对速度; q_j为节点j通信载荷带宽的实时负载率, 且q_j∈[0, 1);k₁~k₄为4个等效距离变量的加权指标, 依据实际物理系统设置。据此, 就可以建立无人机群间双向通信等效距离连接图, 如图 2所示。

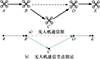图1

点到点通信建链图示

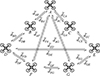图2

无人机群间双向通信等效距离连接图示

1.2 分布式自组织网络拓扑

无人机集群每隔固定周期T进行一次集群内部网络优化, 即进行通信网络自组织拓扑。网络拓扑方法的实现主要基于节点间的局部相互作用和分布式决策。无人机节点在初始化阶段通过感知和通信能力发现周围的邻居节点, 并建立邻居表以维护连接信息。随后, 无人机集群内部定期交换局部信息, 包括状态、资源和邻居列表等, 以支持局部决策和调整。根据收集到的信息和调整策略, 每个无人机节点进行局部决策, 例如调整连接、选择邻居、资源分配等。随着环境的变化, 无人机节点可以根据实时反馈信息进行调整和优化, 从而保持系统的适应性和稳健性。基本的自组织网络拓扑过程步骤如下:

步骤1 初始化

初始阶段, 网络中的各个无人机节点被部署并初始化。每个无人机节点获取自身的信息, 包括自身位置、邻居节点等。

步骤2 邻居发现

无人机节点通过广播、扫描等方式与周围的邻居节点进行通信, 并发现它们的存在。

步骤3 邻居关系建立

无人机节点与其邻居建立通信关系, 并按照(1)式计算得到它们之间的等效通信距离, 形成双向通信等效距离连接图, 记录与之相邻的无人机节点信息。

步骤4 局部信息交换

无人机节点之间开始交换局部信息, 例如节点的状态、可用资源、邻居列表等。这些信息有助于节点进行自我组织和决策。

步骤5 拓扑调整

根据收集到的信息, 无人机节点通过建立、断开或调整连接, 节点移动等行为, 调整自身的状态或连接关系, 以适应网络的动态变化。

步骤6 拓扑优化

无人机节点根据预定的优化目标, 调整自身的拓扑结构, 以优化整个网络的性能, 涉及到最小化能耗、最大化覆盖范围、最大化数据吞吐量等目标。

步骤7 信息传输

节点根据收集到的信息和预定的策略, 做出局部决策, 通过路径寻优算法选择合适的链路进行信息多跳中继传输。

步骤8 适应性和反馈

无人机节点根据实时的环境变化和反馈信息进行调整和优化, 从步骤2~7周期循环, 以保持系统的适应性和稳健性。

2 基于改进狼群算法的路径寻优

面对大规模无人机集群信息高速传输的需求, 在无人机集群分布式自组织网络拓扑循环调整过程中, 如何快速选择最优路径实现在通信网络中的信息传输, 提高网络整体运转效率成为核心关键, 其本质就是一个多点最优路径搜索问题。本文结合狼群算法设计了一种改进网络寻优算法, 以此提高无人机集群网络通信效率和实时性。

2.1 基于等效通信距离的狼群寻优算法

狼群算法是基于狼群群体智能, 模拟狼群捕食行为及其猎物分配方式, 抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制, 提出一种新的群体智能算法[13–14]。

狼群算法中包括3种角色：头狼、猛狼和探狼, 三者之间可以互相转换。大体而言, 头狼即为当前搜索周期内最优解; 猛狼通过向头狼奔袭, 使自身解向头狼对应解靠近; 探狼则在自身解附近搜索更优解。假设某无人机节点A获取的实时集群等效双向通信连接图中共N个节点, 则基于等效通信距离的狼群寻优算法基本流程如下:

步骤1 初始化狼群

以无人机节点A为起点, 形成M个通信路径P={p₁, p₂, …, p_M}; 结合集群等效双向通信连接图, 就可以计算得出每个通信路径对应的总等效距离D={d₁, d₂, …, d_M}; 则最短距离路径对应解作为“头狼”, 前K个最短距离路径对应解作为“探狼”, 其余解作为“猛狼”。

步骤2 探狼游走

K个“探狼”对应解采用内部节点随机调换模式, 形成新的解; 若新的解对应等效距离小于“头狼”对应解距离, 则“探狼”变为“头狼”角色。

步骤3 头狼召唤、猛狼奔袭

“头狼”通过嚎叫发起召唤行为, “头狼”一定距离内的猛狼以较大的奔袭步长逼近头狼所在位置, 即将“猛狼”对应解向“头狼”对应解调整变换; 若新的解对应等效距离小于“头狼”对应解距离, 则“猛狼”变为“头狼”角色。

步骤4 猛狼围攻

当“猛狼”距离“头狼”较近时, 以较小的步长移动, 在“头狼”附近搜索更优解; 若新的解对应等效距离小于“头狼”对应解距离, 则“猛狼”变为“头狼”角色。

步骤5 迭代循环

重复步骤2~4, 直至达到最大循环次数或连续多次迭代“头狼”解对应等效距离基本不变。

2.2 相关问题改进设计

1) 狼群对应解编码

对于某个无人机节点的通信问题, 其核心是要在短时间内计算出到其他节点的最优通信路径。利用狼群算法进行最优路径搜索时, 每只狼对应该无人机节点至其他各节点的通信路径。则每只狼对应解如(2)式所示。

式中, randperm(N-1)表示随机形成1~N-1的全排列数列。

2) 适应度函数设计

某个解p_i对应的等效距离越小, 则该解的适应度值越大, 因此适应度函数f设计如(3)式所示。

式中: dis(p_i)表示解p_i对应的总等效距离; C_f为常数。

3) 游走行为解调整

“探狼”对应解p采用随机交叉的形式进行调整, 并设定随机调整后对应的适应度值若小于原值, 则放弃随机调整。随机调整公式如(4)式所示。

式中, randperm(N, u)表示在1~N中随机抽取u个数。

4) 奔袭行为解调整

将解p看作N维度空间中的坐标, 则狼群对应解视作N维度空间中的点, 则“猛狼”坐标p_fw向“头狼”坐标p_hw奔袭行为解调整公式为

式中: s_rush表示奔袭步长; p_fw(t+1)的解需要通过向上、向下取整重新调整为N的全排列序列。

5) 围攻行为解调整

“猛狼”距离“头狼”较近后, 进入围攻行为, 即在区域范围内向“头狼”位置小幅度调整, 并设定调整后对应的适应度值若小于原值, 则放弃调整。围攻行为解调整如(6)式所示。

式中: λ∈[-1, 1];s_bes表示围攻步长; p_fw(t+1)的解需要通过向上、向下取整重新调整为N的全排列序列。

6) 调整步长关系

参考传统狼群算法步长设计原则[13–14], 设定步长关系如(7)式所示。

式中, C_s为常数, 约束了人工狼在解空间中的搜索精细程度。

3 验证与分析

3.1 通信效能测试

为证明本文提出的等效通信距离更贴合实际物理通信网络, 分别利用基于等效通信距离的动态路径搜索算法(path searching algorithm based on equivalent communication distance, PSA-ECD)和基于位置距离的动态路径搜索算法(path searching algorithm based on physical distance, PSA-PD), 进行当前节点至其他节点的最优路径选择, 基于该路径进行信息传输, 并对网络信息传输质量进行对比。测试步骤如下:

步骤1 在仿真环境中构建含300节点的通信网络, 并对每个节点随机赋予位置信息、通信载荷负载率状态(设定负载率越高信息传输丢包率越高)、通信延时时间参量, 模拟复杂场景实际通信情况;

步骤2 随机选定某节点A向其他节点发送信息, 对一定时间内网络中的信息传输成功率进行统计(节点A向节点B发送信息, 且节点B收到信息, 记为成功, 否则记为失败);

步骤3 重复步骤1和步骤2 100次, 对比2种算法下的信息传输成功率, 如图 3所示。

由图 3可得, PSA-ECD算法的通信成功率比PSA-PD算法的要高, PSA-ECD平均成功率为92.47%, PSA-PD平均成功率为78.61%。因此, 基于本文提出的等效通信距离进行网络拓扑时, 具有更高的通信效能。

图3

通信成功率对比

3.2 算法效能测试

对于无人机集群协同问题, 通信的实时性最为重要, 本文提出采用改进狼群算法就是为了进一步提升集群网络拓扑的效率。据此, 将本文提出方法(NTM-WPA)与基于弗洛伊德算法的网络拓扑方法[8–9](network topology method based on floyd algorithm, NTM-Floyd)、基于迪杰斯特拉算法的网络拓扑模型[10–11](network topology method based on dijkstra algorithm, NTM-Dijkstra)进行对比, 通过一系列蒙特卡洛(Monte Carlo)测试, 以验证本文方法在网络拓扑问题中的实时性和效率。测试步骤如下:

步骤1 通过随机生成100张包含300节点的网络双向连接图, 点与点之间赋予随机权重;

步骤2 随机选定某节点A, 分别利用3种方法获取A节点至其他299个节点的最短路径;

步骤3 每张图重复50次步骤2, 即选定50次初始节点。最终, 每个算法记录100张连接图共计50 000次搜索时间。

3个算法搜索效率对比如图 4~6所示。

根据图 4~6, 50 000次搜索对比下, NTM-WPA、NTM-Dijkstra和NTM-Floyd算法平均搜索时间依次为261.85, 298.95, 375.47 ms, 平均方差依次为2 531.8, 3 346.5, 5 099.6, 平均搜索时间极差依次为167.19, 191.87, 239.94 ms。综上, 表明本文提出的NTM-WPA算法具有更低的运行时间和更快的搜索效率, 并且搜索时间更稳定。

图4

搜索时间均值对比

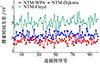图5

搜索时间方差对比

图6

搜索时间极差对比

3.3 实际场景测试

实际场景下主要对通信网络实用性进行考核, 本文利用多蓝牙组合方式模拟无人机间网络通信, 构建网络连接图, 进行该状态下的网络拓扑能力测试。具体步骤如下:

步骤1 设置5对蓝牙模块组{{A₁, A₂}, {B₁, B₂}, {C₁, C₂}, {D₁, D₂}, {E₁, E₂}}, 每组蓝牙组合只能实现与自身配对蓝牙的通信, 即X₁仅能与X₂通信;

步骤2 模拟5台无人机, 对蓝牙模型进行无人机分配, 具体如下: Q₁={A₁, B₁}, Q₂={A₂, C₁, D₁}, Q₃={B₂, C₂, E₁}, Q₄={E₂}, Q₅={D₂}, 如图 7所示。

其中, 当2台无人机间具备蓝牙通信能力时, 其距离可以通过通信相位差进行计算获取, 本次测试将各无人机间距离统一, 均为1 000 cm。

步骤3 利用NTM-WPA算法进行网络拓扑测试, 以Q₁为无人机集群与后台控制中心的通信关键节点, 将获取到的各节点信息以及该信息的经过路径进行展现。

通过试验, 获得信息如图 8所示，则面对弱连接环境, 只要节点间存在一条多跳连通网路, 即可完成各节点间数据通信。由此, 证明NTM-WPA算法在弱连接环境下具有一定的抗毁伤能力和实用性, 能够继续进行数据共享和任务执行。

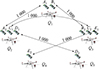图7

无人机集群弱连接通信环境图示

图8

无人机集群弱连接通信环境通信共享信息截图

4 结论

本文提出了一种基于狼群算法的集群通信自组织拓扑方法NTM-WPA, 该方法用于提升无人机集群实际物理网络通信环境下的网络拓扑效率, 确保无人机集群稳定可靠通信。通过仿真实验和实物测试验证了本文方法的有效性及其在路径搜索中具有更高的搜索效率, 对实际场景也有较好的适应性, 具有一定的推广应用价值。

References

ARAF S, SAHA A S, KAZI S H, et al. UAV assisted cooperative caching on network edge using multi-agent actor-critic reinforcement learning[J]. IEEE Trans on Vehicular Technology, 2022, 72(2): 2322–2337 [Google Scholar]
CHEN Mou, MA Haoxiang, YONG Kenan, et al. Safety flight control of UAV: a survey[J]. Robot, 2023, 45(3): 345–366 (in Chinese) [Google Scholar]
ZHENG Bo, TANG Wenxian. Current status and trends of global drone industry development[J]. Dual Use Technologies & Products, 2014(8): 8–11 (in Chinese) [Google Scholar]
TIAN Yuan, WU Feng, OUYANG Jun, et al. Analysis of progress in unmanned aerial vehicle communication and standards for low altitude economy[J]. Information and Communications Technologies, 2023(5): 38–44 (in Chinese) [Google Scholar]
DUAN Z, WEI A, ZHANG X. Sampled-data secure group consensus for nonlinear multi-agent systems in fixed/switching topologies[J]. IEEE Systems Journal, 2023, 18(1): 737–745 [Google Scholar]
WANG M, WANG R. Group consensus of fractional order multi-agent systems with fixed topology[C]//2017 Chinese Automation Congress, 2017: 331–336 [Google Scholar]
KASAN H, KIM J. The case for dynamic bias in global adaptive routing[J]. IEEE Computer Architecture Letters, 2021, 20(1): 38–41 [Google Scholar]
ZHANG X. Power: multi-capatibility adaptive routing for network-an-chips[C]//2023 3rd International Conference on Neural Networks, Information and Communication Engineering, 2023: 751–754 [Google Scholar]
LIU C. Strong correlation fuzzy clustering analysis of regional industrial structure network based on floyd improved algorithm[C]//2023 4th International Conference for Emerging Technology, 2023: 1–6 [Google Scholar]
ZHOU Y, LONG L, LIN Y. Application research of "vehicle+UAV" mode based on Floyd and genetic algorithm in 5G era[C]//2023 IEEE International Conference on Image Processing and Computer Applications, 2023: 1705–1709 [Google Scholar]
ZHOU P, XIE Z, ZHOU W, et al. A heuristic integrated scheduling algorithm based on improved Dijkstra algorithm[J]. Electronics, 2023, 12(20): 4189 [Google Scholar]
JABBAR L S, ABASS E I, HASAN S D. A modification of shortest path algorithm according to adjustable weights based on Dijkstra algorithm[J]. Engineering and Technology Journal, 2023, 41(2): 359–374 [Google Scholar]
LIU Hailong, LEI Bin, WANG Wanying, et al. An improved fusion genetic grey wolf optimization algorithm for solving TSP problems[J]. Computer Simulation, 2023, 40(9): 333–338 (in Chinese) [Google Scholar]
CHENG Jun, DONG Xueping, ZHANG Zhijun. AGV path planning based on improved wolf pack algorithm[J]. Journal of Hefei University of Technology, 2023, 46(7): 879–885 (in Chinese) [Google Scholar]

All Figures

	图1 点到点通信建链图示
In the text

	图2 无人机群间双向通信等效距离连接图示
In the text

	图3 通信成功率对比
In the text

	图4 搜索时间均值对比
In the text

	图5 搜索时间方差对比
In the text

	图6 搜索时间极差对比
In the text

	图7 无人机集群弱连接通信环境图示
In the text

	图8 无人机集群弱连接通信环境通信共享信息截图
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] ARAF S, SAHA A S, KAZI S H, et al. UAV assisted cooperative caching on network edge using multi-agent actor-critic reinforcement learning[J]. IEEE Trans on Vehicular Technology, 2022, 72(2): 2322–2337 [Google Scholar]

[2] CHEN Mou, MA Haoxiang, YONG Kenan, et al. Safety flight control of UAV: a survey[J]. Robot, 2023, 45(3): 345–366 (in Chinese) [Google Scholar]

[3] ZHENG Bo, TANG Wenxian. Current status and trends of global drone industry development[J]. Dual Use Technologies & Products, 2014(8): 8–11 (in Chinese) [Google Scholar]

[4] TIAN Yuan, WU Feng, OUYANG Jun, et al. Analysis of progress in unmanned aerial vehicle communication and standards for low altitude economy[J]. Information and Communications Technologies, 2023(5): 38–44 (in Chinese) [Google Scholar]

[5] DUAN Z, WEI A, ZHANG X. Sampled-data secure group consensus for nonlinear multi-agent systems in fixed/switching topologies[J]. IEEE Systems Journal, 2023, 18(1): 737–745 [Google Scholar]

[6] WANG M, WANG R. Group consensus of fractional order multi-agent systems with fixed topology[C]//2017 Chinese Automation Congress, 2017: 331–336 [Google Scholar]

[7] KASAN H, KIM J. The case for dynamic bias in global adaptive routing[J]. IEEE Computer Architecture Letters, 2021, 20(1): 38–41 [Google Scholar]

[8] ZHANG X. Power: multi-capatibility adaptive routing for network-an-chips[C]//2023 3rd International Conference on Neural Networks, Information and Communication Engineering, 2023: 751–754 [Google Scholar]

[9] LIU C. Strong correlation fuzzy clustering analysis of regional industrial structure network based on floyd improved algorithm[C]//2023 4th International Conference for Emerging Technology, 2023: 1–6 [Google Scholar]

[10] ZHOU Y, LONG L, LIN Y. Application research of "vehicle+UAV" mode based on Floyd and genetic algorithm in 5G era[C]//2023 IEEE International Conference on Image Processing and Computer Applications, 2023: 1705–1709 [Google Scholar]

[11] ZHOU P, XIE Z, ZHOU W, et al. A heuristic integrated scheduling algorithm based on improved Dijkstra algorithm[J]. Electronics, 2023, 12(20): 4189 [Google Scholar]

[12] JABBAR L S, ABASS E I, HASAN S D. A modification of shortest path algorithm according to adjustable weights based on Dijkstra algorithm[J]. Engineering and Technology Journal, 2023, 41(2): 359–374 [Google Scholar]

[13] LIU Hailong, LEI Bin, WANG Wanying, et al. An improved fusion genetic grey wolf optimization algorithm for solving TSP problems[J]. Computer Simulation, 2023, 40(9): 333–338 (in Chinese) [Google Scholar]

[14] CHENG Jun, DONG Xueping, ZHANG Zhijun. AGV path planning based on improved wolf pack algorithm[J]. Journal of Hefei University of Technology, 2023, 46(7): 879–885 (in Chinese) [Google Scholar]