| Issue |
JNWPU
Volume 42, Number 3, June 2024
|
|
|---|---|---|
| Page(s) | 435 - 445 | |
| DOI | https://doi.org/10.1051/jnwpu/20244230435 | |
| Published online | 01 October 2024 | |
Flight situational assessment based on complex network and MFIM-TOPSIS
基于复杂网络和MFIM-TOPSIS的飞行态势评估
1
Air Traffic Control and Navigation College, Air Force Engineering University, Xi'an 710051, China
2
National Key Laboratory of Air Traffic Collision Prevention, Xi'an 710051, China
3
Unit 93220 of the PLA, Harbin 150036, China
4
Unit 95605 of the PLA, Chongqing 402360, China
Received:
13
June
2023
In order to objectively and accurately assess the airborne flight posture in the trajectory-based operation (TBO) mode, a flight posture assessment method based on complex network and MFIM-TOPSIS is proposed. Firstly, the precise protection zone of different aircraft types is established by analyzing the risk of lateral collision between aircraft, and the flight conflict network is constructed by using the three-dimensional velocity barrier method, which is close to the TBO air operation environment, based on which six network topology indexes, such as total node degree, average point strength and network density, are selected to build the flight attitude assessment index system. To weaken the influence of the assessment subjectivity, an interaction matrix that can reflect subjective factors-objective factors is proposed. The maximum information coefficient is used to improve the coding of interaction matrix. Finally the flight attitude level status is assessed by using the superiority-disadvantage solution distance method. The simulation analysis and the example analysis of Takasaki Airport show that the evaluation model can accurately assess the air traffic situation and provide auxiliary information for controllers' decision making and command.
摘要
为了客观准确评估基于航迹运行(TBO)模式下空中飞行态势, 提出了一种基于复杂网络和MFIM-TOPSIS的飞行态势评估方法。通过分析航空器间侧向碰撞风险建立不同机型的精准保护区, 通过三维速度障碍法构建飞行冲突网络, 贴近TBO空中运行环境, 在此基础上选取总节点度、平均点强、网络密度等6个网络拓扑指标构建飞行态势评估指标体系。为弱化评估主观性影响, 提出了一种能反映主观因素-客观因素的相互作用矩阵, 采用最大信息系数对相互作用矩阵编码进行改进, 通过优劣解距离法评估飞行态势等级状况。仿真分析和高崎机场实例分析结果均表明: 该评估模型能够准确评估空中飞行态势, 能为管制员决策指挥提供辅助信息。
Key words: flight conflict network / complex network / flight situational assessment / superior-disadvantage solution distance method / multi-factor interaction matrix
关键字 : 复杂网络 / 飞行冲突网络 / 飞行态势评估 / 优劣解距离法 / 多因素相互作用矩阵
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
随着飞行需求的不断增长, 空中交通流量陡然增加, 有限空域资源与空中运输需求之间的矛盾进一步加深。为了保证飞行安全同时提高空域利用率, 基于航迹运行(TBO)[1]与自由航线空域(FRA)[2]等新一代空管运行概念应运而生。在这种运行模式下, 飞行员可以自主按需规划飞行路径, 促进了空域容量和飞行效率的提升。然而, TBO运行方式下空域用户数量骤增及用户航线的自由规划, 使空情变得更加复杂, 管制员负荷更加繁重。准确客观地评估飞行态势, 能够协助管制人员掌握空域运行动态, 辅助管制员决策指挥, 降低管制员工作负荷。因此, 准确客观评价TBO运行模式下空中飞行态势成为当前业界新的研究热点方向。
态势评估一词最早用于网络安全领域, 旨在通过安全属性的历史记录和运行状况等对系统进行一种精确的安全状况判断以及安全的趋势预测, 使管理部门可以有针对性地做出判断和预防准备[3]。相对应, 飞行态势评估是对当前空中交通情况以及未来一段时间内可能出现的状况进行态势分析、评判、预警和预先处置, 使管制员能够全面、动态、宏观地掌握和预见空中情况。在飞行态势评估方面, 国内外学者将研究集中于空中交通复杂性、飞行安全及空中冲突等问题, 依据复杂性和冲突状况判断空中交通态势。Bronsvoort等[4]提出一种与飞行效率相关的空中交通管理性能评估框架, 通过分阶段确定不同飞行效率水平; 欧韬等[5]利用BP神经网络和Elman神经网络建立民航安全态势评估模型; 杜婧涵等[6]建立了基于度量学习的机场交通态势弱监督评估体系, 准确感知机场场面运行环境; Xiao等[7]提出了一种利用智能算法进行综合分类的空中交通复杂性评估模型, 提高了评估结果的有效性和准确性; 吴明功等[8–11]以飞机间的距离关系构建飞行冲突网络, 引入速度障碍法, 利用网络拓扑指标分析空中交通动态和飞行冲突情况。这种方法是以通信关系或统一间隔标准为依据判定冲突网络连边, 没有依据航空器性能采取不同的间隔标准进行判定, 不能很好地适用于分析TBO运行环境下机型各异的航空器所构成的空中复杂网络。本文在此基础上, 构建了不同机型侧向飞行安全间隔模型, 以此为依据判定飞行冲突关系, 对飞行冲突网络结构做出优化, 更适用于分析TBO运行环境下的空中交通状况。
在态势评估方法方面, 赵嶷飞等[12]基于模糊层次分析法和模糊综合评价法评估航路态势, 方法有较大的主观性; 赵小林等[13]结合层次分析法(analytic hierarchy process, ATP)与优劣解距离法(technique for order performance by similar to ideal solution, TOPSIS)将3个维度的网络安全指标进行综合评价, 消除层次分析法的主观性[13]。胡涛等[14]提出了一种基于改进MGM(1, N)轨迹预测的态势评估方法, 能够有效反映空战态势的变化趋势, 具有良好的预见性; 李昂等[15]提出一种基于相依网络和支持向量机的管制系统运行态势评估方法, 将评估问题转换为分类问题, 降低了主观因素的影响; 温祥西等[16]使用朴素贝叶斯分类算法监测并评估飞行态势, 降低了虚警率。以上研究采用的评估方法存在2个问题: ①确定权重的过程主观性过强; ②所需原始训练样本数量较多。优劣解距离法(TOPSIS)是一种常用的综合评价方法, 它能充分利用原始数据信息进行分析, 适合于处理多因素、多对象的决策问题[17]。因此, 本文选择优劣解距离法评估飞行冲突态势, 引入多因素相互作用矩阵(multi-factor interaction matrix, MFIM)和最大信息系数(maximal information coefficient, MIC)改进优劣解距离法没有考虑评价因素相互作用影响、主观性过重的问题。
综上, 本文在前期工作的基础上[11], 首先构建不同机型航空器精准保护区模型, 以此为依据利用速度障碍法判定网络连边, 确定网络边权, 引入网络拓扑指标作为评价指标, 进而确定飞行态势等级。然后, 通过最大信息系数对MFIM进行编码来确定每个指标的恒定权重, 最后, 运用TOPSIS方法评估TBO运行模式下飞行态势等级。
1 飞行冲突网络
为了分析空中交通情况的复杂性, 评估空中态势, 利用复杂网络理论构建冲突网络G=(V, E, W)。
1.1 冲突网络连边的确定
网络中航空器节点构成连边需满足以下2个条件: ①位置临近, 当2架航空器之间的间隔小于一定范围时, 可能会发生冲突; ②满足速度障碍关系, 即假设一架航空器静止, 并为其设置保护区, 另一架航空器与其相对速度的方向在速度障碍锥内部。
首先在三维的空域中, 为航空器设置椭球形飞行保护区, 依据ATC的间隔标准, 椭球体的长焦距a=10 km, 短焦距c=300 m, 当进入彼此的保护区时则存在冲突。随着通信导航监视性能不断增强、防撞系统不断完善, 在未来基于航迹运行(TBO)模式下, 允许根据航空器性能采取不同的间隔标准, 为航空器划设更为精细的保护区。
飞行过程中, 航空器的飞行轨迹会受到CNS性能、飞行员反应时间和气象风这三大随机因素的影响, 飞行中期望航迹与实际航迹之间的误差服从正态分布, 得到改进后的运动模型, 更加系统、有效地评估最低运行安全标准。
式中:f(·)为飞机质点运动学模型, CNS性能为c~N(0, σcns2); 高空风的随机扰动满足w~N(μw, σw2)[18]; 飞行员反应时间服从伽马分布G(α, λ)[19], 数学期望为α/λ, 方差为α/λ2; DAB为两机的距离。模型引入的三大随机因素间以及两机各自所受随机因素间相互独立。
本文假定两航空器处于同一高度层, 相向飞行, 建立碰撞风险模型并求解两机水平间隔标准。由于高斯随机变量之差仍然服从高斯分布, 所以2架飞机飞行间隔同样服从高斯分布, 两航空器之间的水平欧式距离为  , ΔXt与ΔYt满足高斯分布。
, ΔXt与ΔYt满足高斯分布。
根据文献[20], 侧向碰撞风险计算公式为
式中:NP表示所研究的空域中平均每飞行小时内经过的航空器数;P(t)为两架航空器的碰撞概率。
当dt≤λA+λB时, 则视为两机发生碰撞, 2架航空器的碰撞概率P(t)即两机之间欧式距离dt小于λA+λB的概率, 即P(t)={dt≤λA+λB}, 其中λA和λB为两航空器碰撞球半径, 取两机机身长、翼展长和机身高三者中最大值。可得, CNS性能、飞行员反应时间和高空风导致的侧向碰撞风险CR(t)为
根据ICAO对于空中相撞的安全目标水平(target level of safety, TLS)相关规定[21], 在初始两机水平间隔不断变化情况下, 解出相应碰撞概率CR, 取CR为5×10-9时对应的水平间隔值作为最小水平安全间隔标准LTLS。选用分段区间查找法对最小水平安全间隔进行求解, 可以得到符合精度要求的LTLS。
本文椭球形保护区长轴焦距为以上模型所求得的最小水平安全间隔dl=LTLS, 短轴焦距dv=300 m。设航空器B的坐标为(XB, YB, ZB), 则飞行保护区椭球面可表示为
航空器节点间建立连边通过三维速度障碍模型进行判断, 模型如图 1所示。航空器A和B的速度分别为vA, vB, 利用矢量三角形法得出相对速度vr=vA-vB。由A向航空器B的飞行保护区做切面, 形成的区域称为速度障碍锥。当vr方向在速度障碍锥的内部时, 继续飞行的航空器A将会进入B的飞行保护区, 如不进行调整, 将会有飞行冲突发生。
vr所在的直线方程为
其中, (XA, YA, ZA)表示航空器A的坐标; (vx, vy, vz)为vr的方向向量。联立曲面方程(4)与直线方程(5), 如果存在2个解说明航空器B的飞行保护区与vr所在的直线有2个交点C1和C2; 同时如果有cosγ>0成立, 即γ < 90°, 那么vr的方向在速度障碍锥内部, 航空器节点A和B之间构成连边。
式中, γ表示相对速度vr与航空器A和B的位置向量AB的夹角; |LAB|表示A和B之间的距离。
 |
图1 三维速度障碍冲突探测模型 |
1.2 冲突网络边权确定
飞行冲突网络的连边表示空域中航空器之间潜在的飞行冲突, 而边权要能反映冲突的紧迫程度。定义tc为航空器保持当前的飞行状态, 预计会发生冲突的时间。在设计连边权重时需要满足: ①航空器间距离越小, 相对速度越大, 冲突越紧迫, 连边的权重越大, 即边权随tc的减小而增大; ②随着tc的减小, 飞行冲突的紧迫性变化越来越剧烈, 权重增加的幅度也越来越大; ③考虑到速度障碍法原理和飞行冲突的现实意义, 连边的权重应为正值。
图 1中相对速度延长线vr与椭球保护区有2个交点C1, C2, 记航空器距两交点距离为|LAC1|, |LAC2|, 则有
由于可解脱时间tc与边权是负相关的关系, 结合负指数函数的性质, 定义网络边权
由于tc为正值, 其负指数函数的值域为[0, 1], 能够单位化飞行冲突网络的边权。
2 研究方法介绍
2.1 基于MFIM的指标权重确定
多因素相互作用矩阵(MFIM)最先应用于地质系统工程[22],不仅考虑了每个参数对系统的影响, 还能够体现多因素之间的影响、交互作用, 是应用于复杂系统问题分析的一般方法。
MFIM方法主要包括3个过程: ①对多因素相互作用矩阵进行编码; ②计算每个指标的主观和客观影响程度; ③分配各指标的权重。该方法能充分挖掘指标间的相互关系, 剖析复杂系统的内在因素, 但在矩阵进行编码时通常采用的是专家打分法, 该方法主观性过强, 在某种程度上缺乏科学性。因此, 本文对编码方法进行改进。第一步是将影响因素放在矩阵的主对角线上(前后顺序可以互换)。如图 2所示, 矩阵主对角线下三角的位置(图中绿色部分)用最大信息系数(MIC)填充, 越接近1的值表示两两指标相关性越大, 说明该指标地位越高。
最大信息系数是一种用于描述大量数据中非线性关联的两元素间的相关关系[23]。x, y为2个二维变量, 两者的互信息可以表示为
式中, p(x, y)为x与y的联合概率, 一般情况下, 联合概率计算相对较为困难, 因此在x-y散点图中, 将X轴、Y轴按照(i, j)划分为i行j列, 进行网格化, 在此基础上的互信息计算为
进一步, 两变量之间的相关性MIC定义为
式中:B为所划分网格数目, 是样本数量n的0.6次方,MIC的取值范围为[0, 1], 反映2个变量之间的相关程度。
此外, 矩阵主对角线上三角的位置(图中蓝色部分)用评价值A填充, 采用德尔菲[24]0-1制打分法, 邀请多位专家进行独立打分和评价, 描述各指标之间的强弱关系, 数值越接近1则越重要, 反之重要性越小。
每行非主对角线上的评价值表示主对角线的因子对其他因子的影响, 即主观效应。每列非主对角线上的代码表示主对角线受其他因素影响的因素的影响, 即客观效应。例如, Aij(i≠j)不仅表示因子i在水平方向对因子j的主观影响, 也表示因子j在垂直方向对因子i的客观影响作用。因此, 多因素交互作用矩阵是不对称的。
依据相互作用矩阵的构建原理, 影响因素i的主客观效应程度可按(12)~(16)式计算
式中: n为影响因素的数量; ωa(i)和ωp(i)分别是因子i在MFIM中的主观效应和客观效应的程度; ωA, ωP分别为所有影响因素的主客观效应权重之和; ωAP(i)为结合主客观影响的各指标占总指标的权重值。
 |
图2 相互作用矩阵构成方式 |
2.2 基于优劣解距离法的态势综合评价
在得到各指标权重的基础上, 为了综合评价空中态势, 本文采用优劣解距离法。优劣解距离法是一种常用的综合评价方法, 适合于处理多因素、多对象的决策问题。该方法的基本原理是借助于多目标决策评价问题的“理想解”和“负理想解”, 根据评价指标与理想化目标的接近程序进行排序, 方法步骤如下:
1) 构建标准化决策矩阵。假设一个多因素决策问题有n个评价指标和m个待评价选项。评价指标值形成初始决策矩阵如(17)式所示, 并且需要在矩阵中考虑评估指标的正反性。对于正向指标来说, 数值越大, 评价对象就越理想; 对于反向指数来说, 值越小, 评价对象就会越理想。
由于评价指标的维度不同, 很容易影响评价结果的准确性, 因此有必要对评价指标进行归一化。这里, 选择0-1标准转换方法来消除不同指数之间的维度差异。
对于正向指标, 归一化公式为
对于反向指标, 归一化公式为
通过上述公式构造标准决策矩阵F=(fij)m×n。在这个矩阵中, 所有指数的值都分布在区间[0, 1]中, 并且所有指数都变成了正向指数。
2) 构建加权决策矩阵。将形成的无量纲矩阵乘以每个指标的权重获得加权决策矩阵
式中, rij=wjbij, wj为评价指标的权重, Dij为相互作用矩阵得到的结合主客观影响各指标权重值。
3) 确定加权决策矩阵的最优向量Z+和最劣向量Z-。当指标的值和指标评估呈线性分布时, 最优向量Z+和最劣向量Z-分别由以下步骤得到
式中,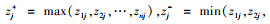
 。
。
4) 计算接近度。使用欧式距离描述样本的差距, 计算样本与理想解之间的接近度来指导决策, 分为与理想解的距离S+和与负理想解的距离S-。
研究对象与评价等级i之间的绝对距离作为评价系数Di, 计算公式为
Di越小, 与评估等级i的接近程度就越大, 就有越大的可能性属于评价等级i。
3 飞行态势评估模型构建
在空域中, 随着航空器数量、速度、航向发生变化, 空中态势也会改变。为准确评估飞行冲突网络态势, 选取能综合反映冲突网络局部和全局信息的指标: 总节点度、平均节点度、平均点强、平均加权聚集系数、网络密度和网络全局效率6个拓扑指标作为影响因素, 利用多因素相互作用矩阵和优劣解距离法对不同情况和状态下的飞行态势进行评估分析。
3.1 态势评估指标
为了全面理解和评估空中交通运行态势, 选择能够多角度反映冲突网络特征的6个复杂网络特征指标对飞行态势进行描述。
1) 总节点度
节点的度定义为网络中某一节点与其他节点链接的数量。在冲突网络中, 节点度能够反映一架航空器与其他航空器之间冲突的个数, 能直观地反映出局部冲突情况, 用ki表示
式中:ki为节点i的度值; N为网络节点总数; aij表示两节点的连接关系, 相连则aij=1, 否则aij=0。
总节点度能反映网络的冲突总数, 用ksum表示
2) 平均节点度
在度值的基础上, 平均度表示整个网络中的每个节点平均与其他节点之间的链接个数, 用k表示
3) 平均点强
点强是度值经过加权后的表达, 该指标不仅能反映相邻节点的数量多少, 还能反映节点周围对该节点的影响程度。在冲突网络中, 平均点强能够反映飞行冲突的紧迫程度, 用s表示
式中:aij表示两节点的连接关系, 相连则aij=1, 否则aij=0;ωij为节点i, j之间的边权。
4) 平均加权聚集系数
加权聚集系数是普通聚集系数的加权表达, 单个数值表示某节点所处位置的聚集程度和节点之间的邻近程度, 而平均加权聚集系数能够反映整个网络的聚集程度。在冲突网络中, 该值可以描述网络整体的冲突汇聚程度, 用C表示
式中, Ci为加权聚集系数, 计算公式为
式中:ki为节点i的度; si为节点i的点强; Δabc为连通三元组的个数; m, n为节点i的邻居节点。
5) 网络密度
网络密度定义为网络中实际存在的连边数与最大可能的连边数之比, 可用于描述网络中节点间相互连边的密集程度, 用ND表示
式中,L为网络中实际的连边数。
6) 网络效率
网络效率在冲突网络中简易地表示出航空器冲突的扩散广度, 定义为
式中: dij为i, j两节点之间的最短路径; 网络效率NE越高, 节点间的联系就越紧密, 网络也相对更复杂。
这6项指标都属于反向指标, 即指标数值越大, 意味着飞行冲突越多, 网络复杂程度越高, 飞行态势越差。
3.2 风险等级划分
分别收集100个不同时刻空中运行态势数据, 依据上述保护区模型和三维速度障碍模型计算不同状态下各项指标作为样本集, 将其划分为“优、良、中、差”4个等级, 同时将评估指标与态势等级对应起来, 评价指标的具体数值等级划分如表 1所示。
评价指标等级划分
3.3 评价指标的相互作用矩阵
空中态势的6个影响因素不是独立作用的, 而是相互作用, 影响飞行态势的好坏。由2.1节所提方法可计算得到多因素相互作用矩阵如图 3所示,蓝色部分为专家打分权重, 绿色部分为最大信息系数权重。
根据MFIM法, 6项指标最终权重及重要度顺序为C(2.86) >k(2.72) >ND(2.63) >ksum(2.30) >NE(2.16)>s(1.85)。每个评价指标经过(16)式的计算, 得到常数权重数组wc={0.158, 0.187, 0.128, 0.197, 0.181, 0.149}。
 |
图3 评价指标的多因素相互作用矩阵 |
3.4 评估模型流程
本文首先选取复杂网络的拓扑指标, 计算各指标之间的最大信息系数, 随后, 引入多因素相互作用矩阵(MFIM), 采用主客观评价值填入矩阵中, 计算综合指标权重, 利用TOPSIS及评价标准等级对飞行态势进行综合评价, 从而评估飞行态势优良。算法流程如图 4所示。
具体步骤如下:
步骤1 构建冲突网络。以飞机为节点, 冲突关系为连边, 利用三维速度障碍法建立冲突网络。
步骤2 选取拓扑指标。依据复杂网络理论, 选取具有代表性的6个拓扑指标, 做标准化处理, 划分飞行态势评价等级及对应的指标范围。
步骤3 确定指标权重。引入多因素相互作用矩阵, 将选取的指标采用德尔菲法[24]原理, 邀请多位专家进行打分和评价, 评价值填入矩阵上三角位置(主观); 计算各指标之间的最大信息系数MIC, 将系数值填入矩阵的下三角位置(客观)。由此, 得到主客观综合评价矩阵, 可由矩阵计算拓扑指标的权重。
步骤4 归一化后的指标乘以权重构建加权决策矩阵, 基于TOPSIS评估等级标准, 确定指标到每个评估等级理想解的距离S+与到反理想解的距离S-, 获得与每一等级的绝对距离, 排序得到与之距离最小的等级, 即飞行态势的等级。
 |
图4 模型设计流程图 |
4 实验仿真与分析
4.1 仿真验证
为了验证评估模型的有效性, 本文通过MATLAB R2020b模拟TBO运行模式下空中态势, 构建一个300 km×300 km的空域, 在空域中随机生成5种不同机型航空器20~80架, 航向任意, 航速在600~900 km/h之间。随机建立30组数据作为监测评估样本, 生成某时刻航空器节点的参数信息后, 根据第1节的不同机型侧向间隔模型生成每一机型不同的“椭球保护区”, 判断航空器间冲突关系, 确定连边权重, 计算网络1~30的6项网络拓扑指标如表 2所示。
在这30组网络拓扑指标数据中, 选出2个较为典型的样本数据进行具体分析, 航空器数量较多的网络24以及航空器数量较多的网络13, 这2个网络中航空器的分布如图 5~6所示, 不同颜色的实心圆代表不同机型的航空器。
在2个飞行态势的拓扑指标值基础上, 采用MFIM-TOPSIS模型得到2组评价态势绝对距离系数结果如表 3所示, 对于网络24而言, D4 < D3 < D2 < D1, 所以网络24的飞行态势差, 容易发生飞行冲突, 造成空中拥堵; 对于网络13来说, D1 < D3 < D2 < D4, 网络13的飞行态势优, 交通状况良好。
将这30组网络拓扑指标输入评估模型中, 对指标进行归一化处理, 得到无量纲矩阵, 乘以常数权重构建加权决策矩阵, 计算到每个评估等级的理想解和非理想解的间距, 计算每组最小绝对距离系数, 得到每组网络的运行态势等级如表 4所示。
样本拓扑指标
 |
图5 较多航空器时的飞行冲突网络图 |
 |
图6 较少航空器时的飞行冲突网络图 |
典型网络评价结果
仿真评估结果
4.2 实例分析
为验证评估模型的有效性和冲突态势等级划分方法的合理性, 选取厦门高崎机场周边管制区雷达态势作为实例进行仿真分析。厦门高崎国际机场位于福建省厦门市, 是我国东南沿海重要的区域性航空枢纽, 同时由于其位置位于我国的东南沿海, 军用飞机也多将其作为任务飞行中的备降机场。获取厦门高崎机场管制区域某日14∶10~14∶40的飞行雷达数据作为实验样本, 间隔10 min记录一次该时段数据, 对记录的空中情况通过MATLAB R2020b进行建模。如图 7所示, 黑色实线表示扇区边界, 不同颜色的实心圆代表不同机型的航空器, 红色实心方块代表高崎机场。
从图 7中可以看出4个时刻的空中交通复杂度和飞行态势变化较小, 14∶30的空情相对较差, 但10 min后得到了缓解。利用这4个场景验证所提出模型的有效性与可行性。运用模型对飞行冲突网络的6个拓扑指标进行计算, 得到结果如表 5所示。
首先利用传统的TOPSIS评估方法对得到的拓扑指标进行评估, 得到的评估结果如表 6所示, D2,D3分别代表飞行态势样本到等级“良”和“中”的最小绝对距离系数。
从表 6可以看出飞行态势由优到差的排序为: 时刻4>时刻1>时刻2>时刻3。
将得到的拓扑指标输入MFIM-TOPSIS评估模型中, 得到评估结果如表 7所示。
从表 7可以看出, 与等级“良”的最小绝对距离系数从小到大排序为: 时刻1 < 时刻4 < 时刻2 < 时刻3, 与等级“中”的最小绝对距离系数从小到大排序为: 时刻3>时刻2>时刻4>时刻1, 所以飞行态势由优到差的排序依次是: 时刻1、时刻4、时刻2和时刻3。在图 7中也能直观看出飞行态势排序为时刻1>时刻4>时刻2>时刻3, 表明由本文方法得到的评估结果相比传统TOPSIS评估方法, 与实际情况更加相符。因此, 本文提出的MFIM-TOPSIS方法由于考虑了评价因素间的相互影响, 更加适用于实际空情中的飞行态势评估, 能够得到较为准确的评估结果。
 |
图7 不同时刻空中运行态势 |
实际场景的拓扑指标
传统方法评估结果
本文模型评估结果
5 结论
本文提出了一种基于MFIM和最大信息系数的模型, 结合优劣解距离法评估基于复杂网络的空中飞行态势。主要创新点如下:
1) 在三维速度障碍法构建的冲突网络基础上, 建立不同机型侧向飞行安全间隔模型以此为航空器划设精准保护区, 优化网络结构, 使之更贴近基于航迹运行模式特点和要求。
2) MFIM方法综合了复杂网络经典指标中的度、点强、集聚系数、特征向量等全局及局部信息, 利用最大信息系数和专家打分法分别考虑了主观影响和客观影响, 弥补了现存方法对飞行态势评估的有限性。
3) 结合TOPSIS方法对评价对象与理想化目标的接近程度进行排序, 确定飞行态势评估等级, 从而一定程度上减少了对专家打分的依赖性, 评估方法具有较好的准确性。
采用不同的间隔标准建立飞行冲突网络, 以空中交通复杂性拓扑指标为评价参数评估飞行态势, 根据MFIM-TOPSIS评价模型将空中运行态势分为优、良、中、差4个等级, 并得到具体的绝对距离系数判断当前飞行态势, 辅助管制员决策, 为以基于航迹运行为核心的空管自动化提供了新思路。
References
- IC AO. Global air traffic management operational concept[J]. DOC 5848-AN458, 2005 [Google Scholar]
- BENTRUP L, HOFFMANN M. Free routing airspace in Europe[C]//Proceedings of the International Conference on Research in Air Transportation, 2016 [Google Scholar]
- CHEN XiuzhenZHENG QinghuaGUAN Xiaohong, et al. Research on security posture assessment of networked systems[J]. Journal of Xi'an Jiaotong University, 2004, 38(4): 76–80 [Article] (in Chinese) [Google Scholar]
- BRONSVOORT JZISSERMANN PBARRY S, et al. A framework for assessing and managing the impact of ANSP actions on flight efficiency[J]. Air Traffic Control Quarterly, 2015, 23(1): 29–53 [Article] [CrossRef] [Google Scholar]
- OU TaoZHOU Changchun. Neural network-based civil aviation security situation assessment model and simulation[J]. China Production Safety Science and Technology, 2011, 7(2): 34–41 [Article] (in Chinese) [Google Scholar]
- DU JinghanHU MinghuaZHANG Weining, et al. Weakly supervised assessment of airport traffic posture based on metric learning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(7): 1772–1778 [Article] (in Chinese) [Google Scholar]
- XIAO M MZHANG JCAI K Q, et al. ATCEM: a synthetic model for evaluating air traffic complexity[J]. Journal of Advanced Transportation, 2016, 50(3): 315325 [Article] [CrossRef] [Google Scholar]
- JIANG X RWEN X XWU M G. A complex network analysis approach for identifying air traffic congestion based on independent component analysis[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 523(1): 364–381 [CrossRef] [Google Scholar]
- WU MinggongWANG ZekunGAN Xusheng, et al. Identification of critical flight conflict points based on complex network theory[J]. Journal of Northwestern Polytechnical University, 2020, 38(2): 279–287 [Article] (in Chinese) [CrossRef] [EDP Sciences] [Google Scholar]
- WU MinggongYE ZelongWEN Xiangxi, et al. A complex network-based method for air traffic complexity identification[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(5): 839–850 [Article] (in Chinese) [Google Scholar]
- BI KexinWU MinggongWEN Xiangxi, et al. Modeling and analysis of flight conflict network based on velocity barrier method[J]. System Engineering and Electronic Technology, 2021, 43(8): 2163–2173 [Article] (in Chinese) [Google Scholar]
- ZHAO Yifei, SHI Yongliang. Traffic situation assessment of airways based on fuzzy comprehensive evaluation[J]. Journal of Civil Aviation University of China, 2011, 29(1): 5–8 [Article] (in Chinese) [Google Scholar]
- ZHAO XiaolinZENG ChonghanXUE Jingfeng, et al. Research on multidimensional network security measurement model based on TOPSIS[J]. Journal of Beijing Institute of Technology, 2021, 41(3): 311–321 [Article] (in Chinese) [Google Scholar]
- HU TaoWANG DongJIANG Longtinget al. Air combat posture assessment based on improved MGM(1, N) trajectory prediction[J]. Electro-Optics and Control, 2020, 27(11): 39–44 [Article] (in Chinese) [Google Scholar]
- LI AngNIE DangminWEN Xiangxi, et al. Operational situation assessment of control system based on dependent network and SVM[J]. Systems Engineering and Electronics, 2021, 43(5): 1287–1294 [Article] (in Chinese) [Google Scholar]
- WEN XiangxiLIN FugenWU Minggong, et al. Flight situation assessment based on complex networks and plain Bayes[J]. Flight Mechanics, 2023, 41(1): 86–94 [Article] (in Chinese) [Google Scholar]
- CLINTON J DJACKMAN S DRIVERS D. The statistical analysis of roll call data[J]. American Political Science Review, 2003, 98(2): 355–370 [Google Scholar]
- MOEK G, LUTZ E, MOSBERG W. Risk assessment of RNP 10 and RVSM in the south Atlantic flight identification regions[R]. MD21401-7465, 2001 [Google Scholar]
- WANG Xin, XU Xiaohao. A preliminary study of lateral separation criteria for airplanes[J]. Journal of Civil Aviation College of China, 2001, 19(1): 1–5 [Article] (in Chinese) [Google Scholar]
- BROOKER P. Longitudinal collision risk for ATC track systems: a hazardous' event model[J]. Journal of Navigation, 2006, 59(1): 55–70 [CrossRef] [Google Scholar]
- ICAO. Convention on International Civil Aviation[R]. DOC 7300, 2006 [Google Scholar]
- LIANG YHE WZHONG W, et al. Objective reduction particle swarm optimizer based on maximal information coefficient for many-objective problems[J]. Neurocomputing, 2018, 281: 1–11 [CrossRef] [Google Scholar]
- LI H WJAMES L. A novel multiple-criteria decision-making-based FMEA model for risk assessment[J]. Applied Soft Computing Journal, 2018, 73: 684–696 [CrossRef] [Google Scholar]
- ROWE GWRIGHT G. The delphi technique as a forecasting tool: issues and analysis[J]. International Journal of Forecasting, 2013, 15(4): 353–375 [Google Scholar]
All Tables
All Figures
 |
图1 三维速度障碍冲突探测模型 |
| In the text | |
 |
图2 相互作用矩阵构成方式 |
| In the text | |
 |
图3 评价指标的多因素相互作用矩阵 |
| In the text | |
 |
图4 模型设计流程图 |
| In the text | |
 |
图5 较多航空器时的飞行冲突网络图 |
| In the text | |
 |
图6 较少航空器时的飞行冲突网络图 |
| In the text | |
 |
图7 不同时刻空中运行态势 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


