| Issue |
JNWPU
Volume 42, Number 3, June 2024
|
|
|---|---|---|
| Page(s) | 446 - 452 | |
| DOI | https://doi.org/10.1051/jnwpu/20244230446 | |
| Published online | 01 October 2024 | |
An airborne radar sea clutter spectrum parameters estimation method based on intelligent learning
基于智能学习的机载海杂波谱参数估计方法
1
School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710072, China
2
Hangzhou Hikvision Digital Technology Co., Ltd., Hangzhou 310051, China
Received:
25
May
2023
Traditional airborne radar sea clutter suppression methods have a high degree of human participation and large errors in estimating the clutter power spectrum. With the development of modern signal processing and artificial intelligence, deep learning methods are used to study the sea clutter more quickly and intelligently. This paper proposes an airborne radar sea clutter spectrum parameter estimation method based on intelligent learning. It establishes a sea clutter training model based on the one-dimensional LeNet-5. Then the simulated and measured sea clutter data are input into the trained model to estimate the center and width of the power spectrum, thus realizing the direct perception of the sea clutter spectrum characteristics. The experimental results show that the proposed method has a higher estimation accuracy and better robustness than the traditional methods.
摘要
传统机载雷达海杂波的抑制方法在估计杂波功率谱时存在人工参与度高、误差大等问题, 导致环境适应性较差。为此, 提出一种基于智能学习的机载海杂波谱参数估计方法, 建立基于一维LeNet-5的海杂波训练模型, 并将仿真和实测海杂波数据输入训练好的模型后对功率谱的中心和宽度进行估计, 进而实现海杂波谱特性的直接感知。实验结果表明, 与传统方法相比, 文中所提方法具有更高的估计精度以及更好的鲁棒性。
Key words: sea clutter / deep learning / doppler characteristics / parameters estimation
关键字 : 海杂波 / 深度学习 / 多普勒谱特性 / 参数估计
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
机载探测雷达由于机载平台具备飞行高度高、观测范围广等优势, 被广泛应用于海上目标预警探测、海上巡逻、搜救等任务。然而, 由于机载对海探测雷达工作在下视模式, 对海观测时将不可避免地受到来自不同方向、大面积的强海杂波影响[1], 这无疑加大了对海雷达信号处理的难度。
为提高机载雷达对海面目标探测的性能, 削弱海杂波的不利影响, 研究人员开展了大量海杂波特性认知研究, 分析不同条件下的海杂波变化趋势, 并在此基础上建立精细的回波模型。其中, 海杂波的多普勒谱特性能够反映海面能量特征和运动相位信息, 在海杂波抑制研究中有着不可替代的作用。因此, 研究准确稳健的海杂波谱特性参数估计方法, 能够为有效改进杂波抑制与目标检测算法、优化雷达系统设计提供充分的依据[2–6]。
传统杂波谱估计方法通常结合数理统计(矩估计、极大似然估计等)进行参数计算, 并借助统计结果对海杂波进行参数估计, 在此基础上设计杂波抑制滤波器[4]。然而, 现有方法存在海杂波先验信息获取困难、杂波协方差矩阵估计人工参与度高、误差严重等问题, 极大程度上限制了杂波抑制效果。深度学习方法在处理大数量级数据时具有显著优势, 近年来被广泛应用于海杂波抑制、目标检测等方面[5], 其中Fernández等[7]提出了基于BPNN实现对海杂波幅度分布参数的估计; Ma等[8]基于LSTM-NN对海杂波幅度分布参数和幅度均值进行估计; Shui等[9]使用GRNN神经网络提取UHF波段海杂波的散射均值, 均取得了较好的效果。本文在现有工作的研究基础上, 提出了一种基于智能学习的机载海杂波谱参数估计方法, 通过建立一维LeNet-5模型, 将预处理后的仿真、实测海杂波数据输入网络进行训练, 最终将海杂波数据输入到训练完成的网络模型实现海杂波谱特性参数的高精度估计。
1 传统海杂波谱参数估计方法
长期以来, 专家学者为了抑制海杂波、提高海面目标检测性能做了大量的研究工作, 经典的海杂波抑制方法包括动目标指示(MTI)、动目标检测(MTD)和空时自适应处理(STAP)。然而, 在强海杂波复杂环境中, 杂波的多普勒频率通常不为零, 文献[3]通过自适应地调整滤波器的凹口位置形成陷波, 实现对杂波的有效抑制。在实际应用中, 自适应杂波滤波器首先估计海杂波功率谱的中心和宽度, 根据谱参数调整滤波器凹口, 故谱中心和谱宽的估计精度直接影响着自适应滤波器的性能。
海杂波的功率谱中心指在功率谱上杂波信号频段的中心位置, 谱宽指杂波频段占用的功率谱宽度。传统的杂波谱中心估计方法包括基于FFT的选大法和质心法, 杂波谱宽估计方法为积分法, 然而, 以上方法对于谱中心和谱宽的不同定义导致不同方法得到的参数值存在较大误差。
1) 基于FFT的选大法
使用周期图法对杂波功率谱数据进行估计, 将功率谱数据最大值点对应的频率作为谱中心。假设杂波序列为x(n), 采用周期图法得到的杂波功率谱为S(k), 则
式中: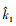 
为谱中心估计结果; N1为数据长度。
由于周期图法本身方差较大, 导致估计误差较大。针对上述问题, 有学者提出根据先验信息先对谱中心范围进行粗略估计, 在此基础上选取功率谱最大值点作为谱中心, 即
式中: [N2, N'2]是根据先验信息粗估得到的谱中心范围;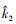 
为谱中心估计结果。
2) 质心法
对于高斯型海杂波功率谱, 越接近谱中心的谱线幅值越大。按其幅值对相应频率进行加权以显示杂波信号真正的功率谱中心。其对应表达式为
式中: [N3, N'3]为利用先验信息估计的功率谱范围；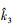
为质心法求得的谱中心。
3) 积分法
假设海杂波功率谱符合高斯分布, 根据正态分布的性质可得
式中: σf为要估计的海杂波功率谱谱宽; F(x)为正态分布的分布函数。
由(4)~(5)式可知, 对于高斯型海杂波功率谱, 可认为在[-σf, +σf]内的杂波能量占总能量的68.26%。积分法先计算海杂波的功率谱中心, 并设定合适的阈值，以上述谱中心为原点向两侧累计能量, 当累计能量与总能量比值达到阈值时, 得到功率谱谱宽。
2 基于一维LeNet-5模型的机载海杂波谱参数估计方法
机载对海探测雷达工作时将面临大面积的海杂波干扰, 其中机载雷达海杂波回波强度大、多普勒频谱展宽, 将严重制约机载雷达对海上目标的检测性能。同时, 由于海洋环境、雷达参数等因素的影响, 现有传统的参数估计方法不能满足多样化的杂波特性研究需求[10]。因此, 建立准确的海杂波谱参数估计模型, 能够实现对海杂波谱特性准确分析, 有助于后续雷达杂波抑制滤波器的设计与实现。
针对传统机载雷达海杂波谱参数估计不准确、人工参与度高的问题, 为实现海杂波谱参数快速、高效的智能化估计, 本文提出一种基于智能学习的机载海杂波谱参数估计方法。所提方法首先对原始海杂波回波数据进行预处理, 并且建立一维LeNet-5网络模型, 再将预处理后的海杂波数据集作为样本输入到一维LeNet-5网络进行模型训练。最后, 将待估计的海杂波数据输入训练完成的网络模型实现对海杂波功率谱中心和谱宽的自主感知和估计。所述方法的具体实现过程如图 1所示。
 |
图1 本文方法具体实现过程 |
2.1 海杂波数据预处理
在进行海杂波谱参数估计前, 需要先构建用于训练和测试验证的海杂波数据集。本文综合采用仿真数据和实测数据建立海杂波数据集, 其中仿真数据通过SIRP法完成不同海况下条件下的K分布海杂波模拟[11], 其中采用SIRP法仿真的海杂波概率密度曲线如图 2所示。
数据预处理与数据集的构建步骤为:
1) 基于SIRP法, 通过设定K分布海杂波的形状参数、尺寸参数和雷达工作参数, 产生3 000组涵盖5级海况的仿真海杂波数据;
2) 对海杂波数据进行脉冲压缩处理, 提高回波信号的信杂比;
3) 计算实测数据的谱中心和谱宽, 并将计算结果作为标签保存到相应文件;
4) 将预处理后得到的海杂波数据与谱中心、谱宽建立对应关系, 完成对数据集的标注;
5) 将带标签的数据集按照7∶3划分为训练集和测试集, 作为样本输入。
 |
图2 不同海况下海杂波的概率密度曲线 |
2.2 模型结构与参数设置
不同于传统卷积神经网络(CNN)在二维图像像素点间结构特征提取方面的优势, 本文直接针对海杂波的一维时域回波信号进行处理。相比传统的CNN模型, 使用一维卷积核的一维LeNet-5网络卷积窗口更大, 计算代价更小, 适用于提取一维的海杂波序列结构特征。因此, 本文采用一种改进的一维LeNet-5模型实现海杂波谱参数估计。具体地, 一维LeNet-5网络结构包含以下模块：
1) 输入层, 使用预处理后的海杂波序列作为原始输入。
2) 2个卷积模块(都包含批量规范化层、ReLU激活层和池化层)。经典LeNet-5模型的卷积核不能适应一维海杂波时间序列分析的需求, 本文为处理一维海杂波数据, 对经典LeNet-5模型进行改进, 将二维卷积核改为一维向量, 利用卷积、参数共享、池化等操作提取海杂波功率谱特征。
3) 经典LeNet-5模型包括3个卷积层, 在处理较大规模数据如海杂波时需要占用的计算资源过大, 本文所提算法减少了卷积层的数量, 在卷积后使用随机丢弃(Dropout)层和全连接层, 降低计算量的同时防止发生过拟合。
图 3为一维LeNet-5的网络结构, 表 1列出了一维LeNet-5各层结构及参数。下面对网络参数设置进行分析: 由于适当的Batch_size可提高模型的泛化能力, Batch_size过大可能导致模型过拟合, 本节Batch_size参数大小设置为100;为避免在优化过程中跳过最优解、训练过程中出现震荡或不收敛, 选择较小的初始学习速率(learning rate)10-5; 加入动量(momentum)以积累之前的梯度信息, 防止掉入局部最优; 优化器选择收敛速度更快、计算效率高的随机梯度下降(stochastic gradient descent, SGD)算法, 配以最小均方差(mean squared error, MSE)作为损失函数。最后, 输出层的输出尺寸为2×1, 表示海杂波功率谱的中心和宽度。
 |
图3 改进的一维LeNet-5网络结构 |
一维LeNet-5参数设置
3 仿真实验结果及分析
3.1 参数估计评价指标
海杂波数据测试集分别使用传统方法和神经网络方法去估计杂波谱中心和谱宽, 使用下面几种评价指标衡量参数估计精度。
1) 皮尔逊相关系数(Pearson correlation coefficient, PR), 皮尔逊相关系数越大表示估计值和实际值越接近, 模型的性能越好。
2) 平均绝对误差(mean absolute error, MAE), 越小估计结果越准确。
3) 均方根误差(root mean squared error, RMSE), 越小估计结果越准确。
4) 平均估计精度η, 越接近1估计效果越好。
式中: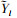 
为谱参数估计值; Yi为实际值; n表示数据总组数。
3.2 仿真实验方案
本节使用的数据集为涵盖5种海况且已添加标签的仿真海杂波数据。每种海况下的训练集和测试集的数据量分别为420段和180段。图 4为使用SIRP法产生的高海况下K分布海杂波。
本节仿真基于Pytorch架构, 搭建的环境选择Python3.9.1, 训练使用设备为GTX1650。在一维LeNet-5网络模型训练至收敛后, 使用测试集对杂波谱中心和谱宽进行测试。图 5为不同迭代次数时, 损失函数的变化情况。
表 2记录本文所提方法与质心法和几种经典网络模型得到的预测结果对比, 表 3记录本文所提方法与积分法[4]和经典模型得到的预测结果对比。
由表 2~3可以看出, 对于谱中心的估计, 一维LeNet-5模型的平均估计精度η达到89.6%, 效果最好, RNN和质心法其次, BPNN的估计效果相对较差; 对于谱宽的估计, 一维LeNet-5模型和RNN具有较好的估计效果, 平均预测精度η分别达到87.5%和82.7%, BPNN和积分法的效果相对一般。表 4给出了不同海况条件下本节提出方法得到的预测结果对比。
由表 4的结果可以看出, 本文所提方法对不同海况杂波的谱特性参数均有较好的估计效果, 具有较好的鲁棒性, 能够应用到更广泛的海洋环境。
 |
图4 仿真K分布海杂波数据 |
 |
图5 训练损失函数变化曲线 |
不同方法谱中心估计结果对比
不同方法谱宽估计结果对比
不同海况条件下谱特性参数估计结果
3.3 实测数据验证结果
本节使用真实雷达数据集验证提出算法模型的有效性。所用实测雷达数据集为1998年MacMaster大学X波段IPIX雷达数据, 该雷达位于安大略湖岸边的格里姆斯比。本文使用22#数据集的4种极化数据(HH, VV, HV和VH)。X波段IPIX雷达的主要参数见表 5, 其他详细参数可在MacMaster大学主页查看或下载。
对估计效果最好的一维LeNet-5模型, 取IPIX雷达实测数据纯杂波单元回波, 划分1 000组序列进行测试。其谱参数估计误差分布直方图如图 7所示。
实测数据真实功率谱中心均值约为120 Hz, 谱宽均值约为130 Hz。由图 7可看出模型误差分布直方图都相对靠近中心0误差区间: 超过85%的序列谱中心预测误差小于7 Hz, 超过91%的序列谱宽预测误差小于7 Hz, 可以判断由所提模型得到的谱参数估计误差较小, 达到了较高的估计精度。
 |
图6 实测IPIX雷达海杂波数据 |
主要雷达参数
 |
图7 基于一维LeNet-5的谱中心、谱宽估计误差直方图 |
4 结论
本文提出了一种基于一维LeNet-5模型的海杂波谱特性参数智能化估计方法, 实现对海杂波功率谱的中心和宽度的精确预测。实测数据结果表明, 与传统方法相比, 本文所提方法的预测性能有明显提高, 估计结果的鲁棒性更好。若在此基础上再设计合适的滤波器权重系数, 能够达到更明显的杂波抑制效果。
References
- DUK V, ROSENBERG L, NG B W H. Target detection in sea-clutter using stationary wavelet transforms[J]. IEEE Trans on Aerospace and Electronic Systems, 2017, 53(3): 1136–1146 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- ROSENBERG L, WATTS S. Coherent detection in medium grazing angel sea-clutter[J]. IET Rader, Sonar and Navigation, 2017, 11(9): 1340–1348 [Article] [CrossRef] [Google Scholar]
- LIU Ningbo, JIANG Xingyu, DING Hao, et al. Summary of research on characteristics of radar sea clutter and target detection at high grazing angles[J]. Journal of Electronics & Information Technology, 2021, 43(10): 2771–2780 (in Chinese) [Google Scholar]
- FAN Y, LI C, LI D, et al. A novel sea clutter suppression method based on neural network[C]//2021 IEEE 4th International Conference on Electronic Information and Communication Technology, 2021: 437–440 [Google Scholar]
- ZHANG Yushi, LI Xiaoyu, ZHANG Jinpeng, et al. Sea clutter spectral parameters prediction and influence factor analysis based on deep learning[J]. Journal of Radars, 2023, 12(1): 110–119 (in Chinese) [Google Scholar]
- ZOU Zhengxia, SHI Zhenwei. Ship detection in spaceborne optical image with SVD networks[J]. IEEE Trans on Geoscience and Remote Sensing, 2016, 54(10): 5832–5845 [Article] [CrossRef] [Google Scholar]
- FERNÁNDEZ J R M, VIDAL J D L C B. Improved shape parameter estimation in K clutter with neural networks and deep learning[J]. International Journal of Interactive Multimedia and Artificial Intelligence, 2016, 3(7): 96–103 [Article] [CrossRef] [Google Scholar]
- MA Liwen, WU Jiaji, ZHANG Jinpeng, et al. Sea clutter amplitude prediction using a long short-term memory neural network[J]. Remote Sensing, 2019, 11: 2826 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- SHUI Penglang, SHI Xiaofan, LI Xin, et al. GRNN-Based predictors of UHF-band sea clutter reflectivity at low grazing angle[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1–5 [CrossRef] [Google Scholar]
- HUANG Penghui, ZOU Zihao, LIU Xingzhao, et al. Robust sea clutter suppression method for multichannel airborne radar[J]. Journal of Electronics & Information Technology, 2021, 43(9): 2680–2687 (in Chinese) [Google Scholar]
- ZHANG Baobao, WU Shunjun. Simulation of coherent K-distribution sea clutter based SRIP[J]. Radar Science and Technology, 20066): 344–347 (in Chinese) [Google Scholar]
All Tables
All Figures
|
图1 本文方法具体实现过程 |
| In the text | |
|
图2 不同海况下海杂波的概率密度曲线 |
| In the text | |
|
图3 改进的一维LeNet-5网络结构 |
| In the text | |
|
图4 仿真K分布海杂波数据 |
| In the text | |
|
图5 训练损失函数变化曲线 |
| In the text | |
|
图6 实测IPIX雷达海杂波数据 |
| In the text | |
|
图7 基于一维LeNet-5的谱中心、谱宽估计误差直方图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.