| Issue |
JNWPU
Volume 41, Number 1, February 2023
|
|
|---|---|---|
| Page(s) | 73 - 80 | |
| DOI | https://doi.org/10.1051/jnwpu/20234110073 | |
| Published online | 02 June 2023 | |
Central node selection algorithm of minimizing maximum weighted response time based on dynamic programming
一种基于动态规划的最小化最大加权响应时间的中心控制节点选举算法
School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710072, China
Received:
19
May
2022
In order to minimize the maximum weighted response time for any node in the network to reach the central control node, a central control node election algorithm based on dynamic programming is proposed. Firstly, the response times of nodes and links in the wireless network are modeled as the node weights and edge weights in the network topology, and then the central control node election problem that minimizes the maximum weighted response time for any node in the network to reach the central control node is modeled as the central problem, where represents the number of central control nodes. Then, by using the interpolation method based on dynamic programming, the weighted response time between the two points can be obtained, and the K-central problem modeled is transformed into several R-control set problems. Then, several control R-set problems are transformed into several 0-1 integer programming problems, and each integer programming problem can be solved one by one by using the branch and bound method. Finally, a simplified implementation method based on the above algorithm is given when K=1, the optimality of the proposed algorithm is proved and the complexity of the algorithm is analyzed. Simulation results show that the proposed central control algorithm can minimize the maximum weighted response time of the network.
摘要
为了最小化网络中任意节点到达中心控制节点的最大加权响应时间, 提出了一种基于动态规划的中心控制节点选举算法。无线网络中的节点和链路的响应时间被建模为网络拓扑图中的节点权值和边权值, 进而最小化网络中任意节点到达中心控制节点的最大加权响应时间的中心控制节点选举问题被建模为K-中心问题, 其中K表示中心控制节点的个数。采用基于动态规划的插点法可求出任意2个点之间的最小加权响应时间, 所建模的K-中心问题被转化为若干个R-控制集问题。将若干个R-控制集问题转化为若干个0-1整数规划问题, 采用分支定界的方法逐个求解每个整数规划问题。给出了K=1时上述算法的简化实现方法, 证明了所提算法的最优性并分析了算法的复杂度。仿真结果表明, 所提算法选举的中心控制算法可最小化网络最大加权响应时间。
Key words: wireless network / central node selection / dynamic programming
关键字 : 无线网络 / 中心节点选举 / 动态规划
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
在无线网络协议架构中, 基于传统的开放互联系统模型[1](open system interconnection, OSI)的分层标准结构, 人们提出了基于平面的标准结构下的软件定义网络(software defined network, SDN)结构模型。该结构模型将开放的互联系统分为控制面和业务面, 提供了在基于OSI模型结构下传统通信中插入调度系统的可能。在调度系统中存在统一的中心控制节点集是关键, 中心控制节点集负责整体网络调度以及协调工作。例如, 在无线网络中进行频点优化、路由优化, 在复杂的物联网环境中负责分配带宽资源等, 而在弹性通信网络中, 需要快速地在弹性组织网络中选举一个中心控制节点集。因此, 在自组织网络下, 中心控制节点集的选举就十分重要。
国内外对中心控制集的选举问题做了大量的研究, 文献[2]将参照能量和点对点的传输时间作为评估标准进行中心控制节点自选举; 文献[3]在网络拓扑中的任一节点获取自身的加权平均值进行自选举, 该加权平均值用来描述所述网络中节点作为中心节点的适合程度; 文献[4]是一种分布式中心控制节点选举方法,将最高节点度数(即节点的一跳邻居节点数)作为标准; 文献[5]使用节点的剩余能量, 集群范围内活动的邻居节点的数量以及节点与基站之间的距离来计算成为簇头的几率; 文献[6]通过动态规划下计算树状网络的控制集完成中心控制节点选举; 文献[7]在多重竞争下根据能量、邻节点的个数以及与已选簇头的距离来决定簇头的位置; 文献[8]将节点度和介数中心性抽象成领导因素, 再由领导因素通过算法找到簇头节点; 文献[9]基于混沌粒子群算法下, 对低功耗自适应集簇型分层协议(low energy adaptive clustering hierarchy, LEACH)进行改进; 文献[10]利用遗传算法在LEACH上改进。
现有研究尚存在下述不足。首先, 现有工作未对最小化最大响应时间进行研究, 而在现有的工业物联网、家庭物联网等无线接入网络中, 节点移动性不强, 无法保障时延性能, 因此, 考虑最小化响应时间具有重要研究意义; 其次, 部分算法基于LEACH协议, 该算法具有随机性, 即使是改进后也有可能选举到非最优点; 最后, 部分可选举最优节点的算法只适用于树状拓扑, 且只适用于点权值为正数下的情况。
本文针对网络中最大加权响应时间的最小化问题, 提出了适合于无线网络下的中心控制节点自选举方案。首先, 将最小化最大响应时间的中心控制节点选举问题建模为K-中心问题, 其中K表示中心控制节点的个数。然后, 基于动态规划的插点法, 求出任意2个点之间的距离, 从而将所建模的K-中心问题转化为若干个R-控制集问题。接着, 将若干个R-控制集问题转化为若干个0-1整数规划问题。最后, 对每个0-1规划问题采用分支定界法进行求解, 并设计了一种适用于K=1时的简化算法, 当K>1时时间复杂度为O(nK+2log2n), 而当K=1时时间复杂度可降为为O(n3)。
1 系统建模
1.1 无线网络描述
无线网络可建模为无向加权网络图T=(V, E; f, w), 其中E是网络拓扑中各个节点之间的链路的集合, V是网络图T中各个节点的集合。映射w: V→{x∈R|x≥0}表示点到权值的映射, 该权值称为点权值, 用以描述节点处理数据包所需的时间, 该权值越大表示该节点的业务负载越大, 从而导致单个数据包传输时延越大。映射f: E→R+表示链路到权值的映射, 该权值称为边权值, 用以表示一条链路传输包所需的时间, 该权值越大同一个大小的数据包所消耗的传输时间越多。ei与vi分别代表集合E与集合V中的元素, 分别代表了网络图中的链路和节点。
节点vi到vj加权响应时间, 指的是从节点vi发出请求数据包到节点vj收到该请求数据包的时间, 其中包括链路传输的时间和节点中继转发的时间。
1.2 目标函数建立和问题建模
在无线网络中, 根据节点是否具有数据包中继转发功能, 所有节点可被分为桥节点和叶子节点两类, 其中桥节点具有AP或Master网卡而叶子节点不具有AP或Master网卡。不同类型的节点可通过安装不同类型的网卡实现, 表1给出了Wi-Fi网络和蓝牙网络中的网卡类型与节点类型的对照关系。
图1给出了网络连接示意图, 其中节点1, 2, 5为桥节点, 分别装配有Wi-Fi中的AP(access point)网卡或蓝牙Master网卡, 而节点3, 4, 6, 7为叶子节点, 仅装配有Wi-Fi中的STA(station)网卡或蓝牙Slave网卡。节点vi到vj的加权响应时间包括两部分, 链路传输所消耗的时间和节点中继转发的时间, 因此在网络中节点vi到vj的加权响应时间tRsp可写成
公式(1)中, w表示路径空间, 即表示节点vi到vj的路由路径上经过节点vk以及对应的链路ek, 用符号表达为
根据上述分析, 最小化最大加权响应时间的目标优化模型为
其物理含义为, 从节点集合V中选举K个节点为中心控制节点集S, 使得最大的加权响应时间最小。该问题在数学中被称为K-中心问题[11]。
Wi-Fi和蓝牙网络中桥与叶子节点的网卡示例
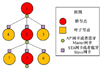 |
图1 网络连接示意图 |
2 算法设计
K-中心问题是一个非确定多项式时间问题(non-determinstic polynomial, NP)问题[12]。K-中心问题是指在无向赋权网络中, 从备选节点中选择K个中心节点, 使其到非中心节点的最大距离最小。
2.1 任意K下基于动态规划的算法设计
2.1.1 基于动态规划的距离d的计算
该算法用于计算全局网络图拓扑的任意节点间的最小加权响应时间, 使用动态规划思路进行求解。
算法核心思想是将所有节点依次插入任意两节点之间, 以求得任意两点间的最小加权响应时间。当所有节点插入完成后, 形成的加权响应时间矩阵为任意节点间最小加权响应时间矩阵, 该矩阵记作矩阵M。根据文献[13]可知, 算法时间复杂度为O(n3)。
2.1.2 K-中心问题的计算方法
根据文献[6]相关内容, 最小化最大加权响应时间问题类似于一个K-中心问题, 该问题是寻找满足要求的中心控制节点集D, 且|D|≤K, 使得全拓扑中节点到达D中的最大加权响应时间r最小。
对于K-中心问题中的最优解r0, 当使用加权响应时间r < r0进行覆盖时, 必然有满足要求的中心控制集合|D|>K, 反之, 对于覆盖的加权响应时间r≥r0, 必存在满足要求的中心控制集合|D|≤K。假设行向量D={d(1), d(2), …, d(n2)}, D中元素为2.1节中M矩阵的元素从小到大排列, 且r0∈D。因此, 利用上述最优解的特点, 并采用二分法迭代求得r0的大小, 其算法流程图如下:
将根据覆盖范围r, 寻找最少中心控制节点个数的问题称为R-控制集问题[6], 最后该K-中心问题就会转换为若干个R-控制集问题。上述算法伪代码如算法1所示。
第一步是计算距离矩阵M, 并将其中元素排列成从小到大的集合D, 第二步是设置初始值, 并计算集合D起始元素是否符合约束条件, 若符合则直接输出, 第三步是采用二分法, 利用覆盖问题的相关性质, 使dU逼近最优解r0, 第四步输出结果。
算法1 K-中心算法:
step1 通过动态规划中的算法求出任何两点间的加权响应时间,并将M中元素从小到大排列成行向量D={d(1), d(2), …, d(n2)};
step2 令U=n2, L=1, r=d(1),执行R-控制集算法,输出控制集D1,若|D1|≠0,则直接跳到step 4输出结果;
step3 while(U>L+1)令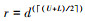 ,利用R-控制集算法计算出输出集合
,利用R-控制集算法计算出输出集合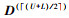 若
若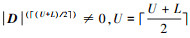 , 否则,
, 否则,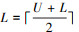
END
step4 若|DU|=k,则直接输出,否则,选举任意剩余节点补充至D。
R-控制集问题中通过2.1.1节动态规划计算任意两点间的加权响应时间, 并得出任意两点间加权响应时间矩阵M, 对于M中的任意元素, 有约束的加权响应时间r, 使得约束矩阵G, 对于∀vi, vj∈E, 若M(vi, vj)≤r, 则G(vi, vj)=1, 否则, G(vi, vj)=0, 1表示vi, vj可以互相覆盖, 0表示节点vi, vj之间无法互相覆盖, 根据相关R-控制集问题的表述[6], 可将问题转化为以下整数规划。设列向量XT=[x1, x2, …, xn], 当xn=1时,对应vn为中心控制节点,当xn=0时,则不是中心控制节点, 对于X有以下整数规划
算式(4)表示最优化目标, 即启用尽可能少的中心控制节点, (5)式表示其约束条件, 即表示选择的中心控制节点集必须至少覆盖一次V中的节点。
根据相关文献[14], 对于该整数规划问题, 可以采用分支定界的思路进行求解, 目标函数的系数全为1情况下, 可以使用隐枚举的方法进行求解[15], 但是该种方法仅针对整数规划进行讨论, 没有结合K-中心问题的一些特性, 借鉴隐枚举中的思路, 增设条件, 若目前枚举的输出集大于要求的K则停止当前分支的枚举, 算法伪代码如算法2所示。
算法2 限定控制集合数量的R-控制集算法:
step1 map←动态规划计算的加权响应时间矩阵,k←K
step 2 for(i < |E|)//变换为约束矩阵
for(j < |E|)
if(map(i, j)≤r) G(i, j)=1
else G(i, j)=0
end
end
step3 //形成空集根层节点,before=0, behind=1, record, i=1, mapTree[0]清空用以表示控制集
while (i≤|E|)
//插入第i号节点,record=behind
while (before < record)
if(mapTree[before]的个数 < k)//一个插入vi节点,另一个不插入vi节点,分别填入mapTree[behind+1]和mapTree[behind+2]中,推进behind,并记录前一个的结果z
//检查前一个的结果
if(z的结果符合约束条件)//结束并输出结果z
end
end
before++
end
//终止条件检查
//若record=behind,则返回空集并终止
End
//返回空集
第一步是变量赋值,第二步是将距离矩阵M变为约束矩阵G,第三步采用分支定界的思路对整数规划问题进行讨论,若没有符合约束条件的解,则输出空集,否则输出可行解。
该算法的核心是当枚举控制集中的个数等于K时,若其不符合约束条件,则其分支不再插入新的节点,当一个结果符合约束条件并小于要求的K时,则认为找到符合要求的解并直接输出。
相较于文献[13]中的算法, 算法1延续了其二分法查找的思想, 算法2主要是改变了对R-控制集问题的求解方法, 文献[13]中使用动态规划将树状网络分层, 再将分层的树状网络逐级求解, 计算出中心节点。算法2使用动态规划方法得出任意节点间的最小加权响应时间, 然后通过整数规划的思路解决问题。相较于之前只适用于求解树状网络拓扑的方案, 本文方案能够求出非树状网络图的K-中心问题, 有更好的适应范围。
 |
图2 算法流程图 |
2.2 K=1下基于动态规划的算法设计
若所求控制集K=1, 可以直接通过矩阵M直接得出结果。
算法3 特殊求解算法
step1 按照动态规划得出矩阵M
step2 Out←∞
step3//找出横排中最大的元素
//找出这些最大中最小的,记为Mi
Out←Mi
该算法的核心思想是先找寻所有节点的最大加权响应时间, 然后将所有节点的最大的加权响应时间进行比对, 找出其中最小的, 选中的节点就是中心控制节点。
算法3仅使用了简单的动态规划求出任意两节点间的加权响应时间矩阵M, 并通过查询直接找出每个节点的最大加权响应时间, 从而获得最小的最大加权响应时间, 相较于文献[13]中的算法, 本算法拥有较低的复杂度, 且适用于非树状网络, 但只适用于K=1时的情况。
2.3 算法性能分析
定理1 在算法2中,若输出为Ø,则不存在一个满足条件的控制集D,使得|D|≤K。
其证明如下(反证法):
若∃D满足最优性, 且|D|≤K, 且D={x1, x2, …, xn-1, xn}, 则存在子集D1={x1, x2, …, xn-1}, 且|D1| < K, 以此类推, 对于Dn-1={x1}, 且|Dn-1| < K, 因此必然能存在推导路径Ø→Dn-1→…D1→D, 与输出集为Ø的结论不符合, 矛盾, 因此结论成立。
定理2 算法1求得结果为最优解。
设该问题的最优值为x0, 而算法1输出值为x1, 在算法3中, 若直接在step2中输出集合|D1|≠0,则该结果没有比起始元素更小,必然为最优解,则必然有x0=x1,若|D1|=0,由于x0时最优的,必然有x0≤x1,而根据定理1中的相关内容,且迭代后有U=L+1, |DL|=0,因此仅当x0≥x1时才存在|Du|≤K,综上所述,x0=x1。
定理3 对于K=k,算法1的时间复杂度为O(nk+2log2n)。
首先,对于K=k的K-问题,算法主要步骤集中在step3的双循环下的演算步骤中,在最差情况下,输出组合为一空集时,终端排列组合的情况有Cnk种解的存在,各自解还有其对应的子集,即一共需要验证kCnk个结果,检查方案为将序列的每个位置与矩阵G中的各个行向量对应相乘,并判断是否均大于1,因此,该部分对应的时间复杂度为O(n2),又因为kCnk < knk,因此该段代码的时间复杂度为O(nk+2)。
接着,对于K=k的算法1问题,step1对于K=k,下动态规划的距离计算方法时间复杂度为O(n3),再将O(n2)个数据排列,则该阶段的时间复杂度O(n2log2n),之后在step2中循环次数为O(log2n),根据定理2总共的时间复杂度为O(nk+2log2n),因此,综合的时间复杂度为O(nk+2log2n)。
定理4 算法3的时间复杂度为O(n3)。
对于算法3,其动态规划的时间复杂度为O(n3),step2中需要对O(n2)进行比较,因此这一步的时间复杂度为O(n2),因此整体的时间复杂度为O(n3)。
3 结果仿真
3.1 仿真系统搭建
首先是比较各种中心控制节点在K=1的等权情况下的仿真效果,仿真系统中有n+1个节点,其中包含1个仅有1个网卡的桥节点、0.25n个多网卡的桥节点的设备、0.75n个叶子节点,n=4, 8, 12, 16, 20。比较在这些情况下的动态规划方案、特殊求解方案、随机中心控制节点方案,测度决定方案的最大加权响应时间的最小值。
其次是比较K=1情况下,非等边权情况下测试各个方案的性能,引入部分蓝牙节点改变边权值,根据带宽计算,Wi-Fi系统的标准带宽为20 MHz,0.75n个终端中,0.25n个是2 MHz带宽的低功耗蓝牙(bluetooth low energy,BLE),0.25n个1 MHz带宽的蓝牙增强速率(enhanced data rate,EDR),0.25n个Wi-Fi,假设Wi-Fi传输的权值为1,则根据蓝牙的带宽与Wi-Fi的带宽比值,蓝牙应当约为10和20,节点个数配置与上一个测试情况一致。
最后在相同连通图的情况下,测试K的变化对提出算法效果的影响,即在节点个数为n=4,8,12,16,20时,测试K=1,2,3,4对仿真结果的影响。
3.2 仿真结果
仿真系统下,节点之间的连接方式如图1中所示,K=1的等权情况下的仿真结果如图3所示。
图3中横坐标代表仿真场景中节点的数量, 纵坐标代表了该方案下产生的中心控制节点的最小化最大响应时间, 数值越大, 网络拓扑中实际最大的加权响应时间越大。该图仿真的是在选择一个中心控制节点并在网络图节点权值与边权值均为1时, 各个方案的性能指标。从图中可知, 随机节点方案其最大相应的均值在同节点数情况下一定大于其他方案, 其他3种方案在节点数小于等于17的结果均一致, 节点数大于17之后, 节点度方案高于特殊求解方案和动态规划方案, 当节点数从5到9时, 由于节点是均匀对称地插入, 最大响应时延没有改变, 如图4所示, 假设节点权值和边权值均为1,节点右上角为该节点对应的最大加权响应时间, 左侧最优的节点为1或者2, 以该节点为中心控制节点最大加权响应时间为4, 而右侧最优为2, 同理最大响应时间为4。
K=1的非等边权情况下的仿真结果如图5所示。
图5中横坐标代表仿真场景中节点的数量, 纵坐标代表了该方案下产生的中心控制节点最小化最大响应时间。该图仿真的是选择一个中心控制节点时, 节点权值为1, 但边权值不一致时各个方案性能的差异, 从图5中可以看出随机节点选举的方案总体大于其他2种方案, 整体随着节点增加而增大, 而节点度方案在n=9时与基于动态规划方案偏离整体大于等于动态规划方案, 并在n=19处出现拐点。
图6中横坐标代表仿真场景中节点的数量, 纵坐标代表了不同K值下产生的中心控制节点最小化最大响应时间。该图仿真选择的是一个中心控制节点时, 节点权值为1, 但边权值不一致时不同中心控制节点数量的性能差异。根据图6所示,K=1的曲线总大于等于其他曲线n=5时, K=2偏离其他曲线, 总体大于等于K=3以及K=4, n=9时, K=3分离, 总体大于等于K=4。
 |
图3 K=1时等权情况最大加权响应时间随节点数量变化曲线 |
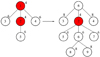 |
图4 插入节点变化图 |
 |
图5 K=1时非等权时最大加权响应时间随节点数变化曲线 |
 |
图6 K≠1时最大加权响应时间随节点数变化曲线 |
4 结论
针对最小化网络中任意节点到达中心控制节点的最大加权响应时间的问题, 本文提出了一种基于动态规划的中心控制节点选举算法。首先, 将无线网络中的节点和链路的响应时间建模为无向加权网络图中的节点权值和链路权值, 并将加权响应时间表示为路径上节点权值与链路权值之和。然后, 采用基于动态规划的插点法可求出任意2个点之间的距离, 将问题转化为多个整数规划问题, 并采用分支定界的方法逐个求解每个整数规划问题。最后, 当K=1时提出了上述算法的简化实现方法, 并证明了所提算法的相关性能。
仿真结果表明, 动态规划与特殊处理法效果优于测度优先以及随机节点选举法。前两者最大加权响应时间, 优于节点度方案与随机节点方案的最大加权响应时间, 具有更好的延时特性。而相较于文献[13]中的算法, 本文中设计的2种算法能够适用于非树状网络拓扑中。
References
- LIN Hua, XUE Jingyi. Research and deployment of software definition network(SDN)/network function virtualization(NFV) technology[J]. Radio and Television Network, 2022, 29(1): 106–108 [Article] (in Chinese) [Google Scholar]
- 杨坤, 吴昊, 刘松洁, 等. 网络中心节点的确定方法、装置及设备节点: 中国, CN108075912A[P]. 2018-05-25 [Google Scholar]
- 孙耀, 高孟杰, 秦爽, 等. 一种基于无线自组织网络的分布式簇头选举方法: 中国, CN110943920B[P]. 2020-10-27 [Google Scholar]
- ABIDI W, EZZEDINE T. Fuzzy cluster head election algorithm based on LEACH protocol for wireless sensor networks[C]//2017 13th International Wireless Communications and Mobile Computing Conference, 2017: 993–997 [Google Scholar]
- DJOUAMA A, ABDENNEBI M. Clusterhead selection algorithm based on energy and mobility in wireless mobile sensor networks[C]//2019 IEEE Symposium on Computers and Communications, 2019: 982-986 [Google Scholar]
- LI Jianping, LIU Xu, ZHU Juanping. R-control set problem and K-center problem in weighted tree network[J]. Journal of Operations Research, 2009, 13(2): 111–118 [Article] (in Chinese) [Google Scholar]
- JIA Yinliang, ZHANG Chiyu, LIANG Kangwu. Cluster head selection algorithm for wireless sensor networks based on multiple competition[J]. Sensors and Microsystems, 2018, 37(2): 140–142 [Article] (in Chinese) [Google Scholar]
- WEI Changbao, CHEN Zhongliang, YAO Ruxian. Cluster head selection algorithm based on fuzzy logic in vehicle network[J]. Measurement and Control Technology, 2016, 35(9): 83–86 [Article] (in Chinese) [Google Scholar]
- LIU Xiaoli, WANG Chuhang, WANG Xue. Improved LEACH algorithm based on chaotic particle swarm optimization[J]. Journal of Changchun University of Technology, 2021, 42(5): 451–454 [Article] (in Chinese) [Google Scholar]
- LIU Tao, PANG Bo. Clustering algorithm for heterogeneous wireless sensor networks based on genetic algorithm[J]. Modern Electronic Technology, 2022, 45(5): 25–30 [Article] (in Chinese) [Google Scholar]
- HAKIMI S. Optimal locations of switching centers and the absolute centers and medians of a graph[J]. Operations Research, 1964, 12(3): 450–459 [CrossRef] [Google Scholar]
- HUANG Shuqiang, JIANG Xiumei, FAN Rensheng. A weighted distance continuous K-center location problem solving method[J]. Minicomputer System, 2020, 41(2): 310–315 [Article] (in Chinese) [Google Scholar]
- LIU Xu. R-control set problem and K-center problem in weighted tree network[D]. Kunming: Yunnan University, 2007 (in Chinese) [Google Scholar]
- HAO Zijun, HE Shanglu. Some discussion on Floyd algorithm for the shortest problem[J]. Journal of Chongqing of Technology, 2008, 138(5): 156–159 [Article] (in Chinese) [Google Scholar]
- YAO Enyu, HE Yong, CHEN ShipingMathematical planning and combination optimization[M]. Hangzhou: Zhejiang University Press, 2001 (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 网络连接示意图 |
| In the text | |
 |
图2 算法流程图 |
| In the text | |
 |
图3 K=1时等权情况最大加权响应时间随节点数量变化曲线 |
| In the text | |
 |
图4 插入节点变化图 |
| In the text | |
 |
图5 K=1时非等权时最大加权响应时间随节点数变化曲线 |
| In the text | |
 |
图6 K≠1时最大加权响应时间随节点数变化曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


