| Issue |
JNWPU
Volume 42, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 117 - 128 | |
| DOI | https://doi.org/10.1051/jnwpu/20244210117 | |
| Published online | 29 March 2024 | |
Research on game strategy of spacecraft chase and escape based on adaptive augmented random search
基于自适应增强随机搜索的航天器追逃博弈策略研究
1
School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
2
National Key Laboratory of Aerospace Flight Dynamics, Xi'an 710072, China
3
Shanghai Aerospace Systems Engineering Institute, Shanghai 201108, China
Received:
29
December
2022
To solve the problem of the survival differential policy interception between a spacecraft and a non-cooperative target pursuit game, the pursuit game policy is studied based on reinforcement learning, and the adaptive-augmented random search algorithm is proposed. Firstly, to solve the sparse reward problem of sequential decision making, an exploration method based on the spatial perturbation of parameters of the policy is designed, thus accelerating its convergence speed. Secondly, to avoid the possibility of falling into local optimum prematurely, a novelty degree function is designed to guide the policy update, enhancing the efficiency of data utilization. Finally, the effectiveness and advancement of the exploration method are verified with numerical simulations and compared with those of the augmented random search algorithm, the proximal policy optimization algorithm and the deep deterministic policy gradient algorithm.
摘要
针对航天器与非合作目标追逃博弈的生存型微分对策拦截问题, 基于强化学习研究了追逃博弈策略, 提出了自适应增强随机搜索(adaptive-augmented random search, A-ARS)算法。针对序贯决策的稀疏奖励难题, 设计了基于策略参数空间扰动的探索方法, 加快策略收敛速度; 针对可能过早陷入局部最优问题设计了新颖度函数并引导策略更新, 可提升数据利用效率; 通过数值仿真验证并与增强随机搜索(augmented random search, ARS)、近端策略优化算法(proximal policy optimization, PPO)以及深度确定性策略梯度下降算法(deep deterministic policy gradient, DDPG)进行对比, 验证了此方法的有效性和先进性。
Key words: non-cooperative target / pursuit game / differential game theory / reinforcement learning / sparse reward
关键字 : 非合作目标 / 追逃博弈 / 微分对策 / 强化学习 / 稀疏奖励
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
近年来, 随着空间交会对接技术的发展, 合作目标自主交会已经逐渐成熟[1-2], 但针对具有自主机动、自主决策能力的非合作目标的交会任务依然存在难度, 此时交会任务可视为航天器间的追逃博弈问题进行分析求解[3-4]。空间航天器间的追逃博弈问题实质上是一个双边控制的连续动态对抗问题, 具有信息层面不沟通、机动行为不配合、先验知识不完备等特征。目前航天器机动主要采用非自主控制, 但博弈过程中航天器若仅依靠地面指挥中心提供指令信息进行机动, 机动的有效性和及时性无法满足任务需求, 安全性和可靠性大幅度降低。因此需要研究针对非合作目标交会对接任务的新方法。
微分对策理论是航天器追逃博弈研究中的主要方法之一。它将现代控制理论与博弈论相结合, 具有较强的竞争性和对抗性[5-7]。针对追逃博弈问题, 微分对策理论的求解方法可以分为基于模型和基于数据驱动2类方法。基于模型的方法依赖于对博弈模型的具体表达式和方程的求解, 通常使用最优控制理论、动态规划等方法。这类方法的特点有:具有较高的控制精度和可靠性, 能够适应不同的任务和环境; 能够提供较为直观的控制指令, 方便对系统进行调试和优化,例如基于线性二次型最优控制, 将问题转化为求解黎卡提方程, 最终得到反馈控制律[8-9]; 可以直接求解两点边值问题所对应的非线性方程组[10]。传统微分对策理论方法在解决航天器追逃博弈问题时需要对航天器的动力学模型进行精确建模, 这样的方法存在误差累积和模型不准确等问题。此外, 传统方法通常假设双方瞬时状态信息完全已知, 这限制了其在逃逸航天器机动规律多变和博弈信息不完全情况下的应用。因此, 传统方法在实际应用中存在一定的局限性[11]。
随着以深度学习、强化学习等为代表的机器学习技术快速发展, 机器学习算法越来越多被应用于博弈问题。朱强等[12]将神经网络用于追逃博弈问题, 提高了计算效率, 减少了计算耗时, 与直接法的优化结果对比吻合较好。曹雷[13]提出了基于深度逆向强化学习、多智能体强化学习、分层强化学习及元深度强化学习等手段的应用模式, 具有重要的理论意义和应用价值。Chun等[14]利用深度Q学习在完成航天器合作交会任务的同时有效规避了碰撞。刘冰雁等[15]为避免应对连续空间存在的维数灾难问题, 通过构建模糊推理模型表征连续空间, 提出了一种具有多组并行神经网络和共享决策模块的分支深度强化学习架构。吴其昌等[16]将训练的深度神经网络作为强化学习的初始结果进行训练, 实现了在线地对网络参数进行调整,减小环境与动力学模型的偏差, 提升了结果准确度。但深度神经网络存在学习参数空间大、数据驱动需求大、算力及能耗要求高等缺点, 在算力、机动能力等受限的任务中难以直接应用。目前的研究主要集中在无限时域或固定时域的追逃博弈任务上, 对于更具对抗性的生存型微分对策问题, 依然以将其转化为一个最优控制问题进行求解的方法为主[17]。这类机器学习场景设计相对简单, 通常采用线性化处理方法。然而, 这种近似方法会引入线性化误差, 并忽略系统整体的非线性特性和复杂性。另外, 在处理复杂环境下的任务时, 强化学习算法面临设计奖励函数的困难, 特别是在稀疏奖励的情况下。稀疏奖励意味着智能体只在特定的时间点或特定的状态下获得奖励信号, 而在其他时间点或状态下没有明确的奖励反馈。这使得学习过程更加困难。因此, 未来的研究需要克服稀疏奖励带来的挑战, 并探索适用于对抗性更强的航天器追逃博弈问题的高效算法。
本文针对强化学习在非线性航天器拦截的追逃博弈求解问题, 发展了一种不依赖神经网络的强化学习方法: 基于增强随机搜索(augmented random search, ARS)算法的思想提出了自适应增强随机搜索(adapt-augmented random search, A-ARS)。该方法直接对策略参数进行扰动, 并设计了新颖度函数以引导策略更新, 从而进一步提升算法的探索能力。此外, 该方法不依赖于复杂的神经网络结构, 从而减少了参数调整的复杂性。数值仿真验证结果表明, 所提出的方法适用于连续控制任务和奖励信号极其稀疏的生存型追逃博弈任务, 进一步证明了该方法的有效性和适用性。
1 追逃博弈模型数学描述
航天器的相对动力学问题在Hill坐标系下描述[18]。Hill坐标系的原点是一个在圆轨道运行的动点, 但并不固定于航天器质心, 而是一个独立以圆轨道运行的假想点, 可在初始时刻定义为逃逸航天器的质心。坐标系X轴沿轨道地心矢径方向, Z轴沿轨道角动量方向, Y轴由左手定则确定(在轨道平面内并指向前进方向)。
当参考轨道为圆轨道, 追逃航天器的博弈在坐标系原点附近进行, 在二体动力学模型假设下状态微分方程可描述为
式中: 下标i=E, P, E代表逃逸航天器; P代表追踪航天器; XP, XE分别为追踪和逃逸航天器相对状态; X=XE-XP=(x, y, z, ẋ, ẏ, ż)T为航天器追逃博弈状态变量; a为轨道半径; μ为地球引力常数; 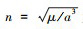 为参考轨道平均角速度; αi和βi分别为推力偏航角和推力俯仰角; Ti为航天器的推力加速度。生存型追逃博弈中, 追踪者期望以最短的时间捕获或拦截目标, 而逃避者期望尽可能延长被捕获或拦截的时间, 双方都仅以时间作为控制指标, 参与博弈的代价函数定义为
为参考轨道平均角速度; αi和βi分别为推力偏航角和推力俯仰角; Ti为航天器的推力加速度。生存型追逃博弈中, 追踪者期望以最短的时间捕获或拦截目标, 而逃避者期望尽可能延长被捕获或拦截的时间, 双方都仅以时间作为控制指标, 参与博弈的代价函数定义为
式中: tf为结束时间。博弈过程中追逃两航天器都将以最大推力加速度TP和TE推进, 此时双方的控制量均为推力加速度方向, 如图 2所示, 推力方向角分别记为uP=[αP, βP]T, uE=[αE, βE]T。
两航天器追逃博弈的目标集为对状态的约束, 设定追逃两航天器的距离小于追踪航天器的最大捕获半径时对策结束, 该值可表示为
在生存型微分对策中, 航天器与非合作目标分别根据当前状态, 将各自的目标函数最小化来获取行为策略。根据博弈论中的纳什均衡理论, 双方行为当且仅当满足不等式(4)时, 行为策略达到纳什均衡
根据微分对策理论[18], 为求解最优必要条件, 构建哈密顿函数
式中: λ为协态变量。控制最优必要条件为
对于追踪航天器, 将(5)式代入(6)式, 只需对控制项计算, 约去常数项后得到
其中二阶判定条件(8)又等价于
当满足(11)式和(12)式2种情况之一时,一阶条件(7)式和(9)式也就同时满足
进一步代入(10)式,证明可得也必然满足(10)式, 即
又因为
上述推导对逃逸航天器同样成立, 最终可得追逃两航天器生存微分对策最优策略的必要条件: 追踪航天器与逃逸航天器最优控制策略相同, 即
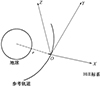 |
图1 Hill坐标系 |
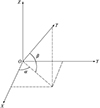 |
图2 航天器推力方向角 |
2 基于A-ARS的追逃博弈
强化学习需要不断在与环境交互过程中接收奖惩信号进行学习, 但强化学习在处理稀疏奖励问题时面临着挑战, 直接将算法应用于该问题存在2个难点:
1) 数据具有欺骗性。没有鼓励探索的机制会使算法过早收敛陷入局部最优中, 甚至无法收敛至可行解;
2) 数据的稀缺性。产生的训练数据有限, 无法计算梯度, 从而降低了以数据驱动的强化学习训练效率。
综上, 数据的欺骗性和稀缺性刺激了高效和广泛探索的需求。强化学习中针对稀疏奖励问题一般采取人为设计奖励、经验回放机制和增强探索利用等方法[19], 但这些方法可能给学习带来错误的引导, 导致策略收敛到局部最优。针对这些挑战, A-ARS强化学习算法针对航天器追逃博弈过程进行采样学习, 并利用有限差分法使用回合累积奖励值进行策略更新。同时, 在搜索和更新步骤上进行改进, 避免过早陷入局部最优解。相比传统的强化学习算法, A-ARS算法在处理稀疏奖励问题方面具有良好的收敛性能。
2.1 增强随机搜索算法
强化学习是一种序贯决策方法, 其过程涉及智能体与环境之间的交互。在数学上, 这个过程被形式化为马尔科夫决策过程(Markov decision process, MDP)。与传统的优化方法不同, 强化学习通过奖励值来指导优化过程。具体而言, 该过程包含以下步骤: 在当前时间步t, 智能体观察到当前状态st, 然后根据当前策略π(a|s)选择行为at并执行; 随后环境转移至下一个状态st+1, 并向智能体反馈奖励rt。最终的目标是寻找一种策略, 使得控制动态系统的平均奖励最大化, 即最大化奖励值的期望
θ表示策略π的参数, ξ表示环境的不确定性, r(πθ, ξ)表示策略π在当前环境下生成的一条状态序列的奖励值。
在生存型微分对策中, 追踪航天器需要不计燃料消耗地在限定时间内尽快靠近目标。当博弈结束时, 根据最后一幕的奖励评估整个决策序列的优劣。然而, 在这类环境中, 由于奖励信号的稀缺性, 基于梯度的算法缺乏足够的数据驱动来学习策略。因此, 本文采用有限差分法更新策略。该方法采用自适应步长策略, 通过近似梯度的多个方向导数进行优化。有限差分法是一种不依赖梯度的优化方法, 也被称为“零阶优化”或“黑盒优化”[20]。与基于梯度的方法相比, 它在处理局部最优和梯度消失等问题时有更好的表现。无梯度优化算法首先在搜索空间中随机初始化一些解, 再从当前可访问的解中建立一个显式或隐式的底层目标函数模型, 该模型隐含一个具有潜在更好解的区域。通过从该模型中采样新的解并更新模型, 无梯度优化算法不断提升解的质量。在这个过程中, 步长可以根据当前策略计算的方差自适应地调整。这种迭代的采样和更新过程被重复执行, 不断改善解的性能。无梯度优化算法通过重复这种采样和更新的过程提高解的质量。策略更新方向表示为
ξ1和ξ2表示2个随机变量值, v表示噪声方差。r(πθi, ξ)表示策略π在当前环境下生成的一条状态序列的奖励值。
图 3a)展示了有限差分法的基本原理。ARS算法将有限差分法中的梯度与导数关系结合起来, 通过使用随机方向的扰动探索策略空间, 实现在没有显式导数的情况下估计梯度, 并建立线性策略模型。图 3b)展示了ARS算法的更新原理。在每一步中, 以当前状态为原点, 算法会在周围的2n个方向上进行探索。通过比较对应相反方向的奖励差异, 选择具有最大奖励差值的k个方向作为下一步的更新方向。这样的更新策略能够引导算法朝着奖励最大化的方向前进。参数更新公式为
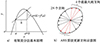 |
图3 有限差分法原理及ARS算法更新示意图 |
2.2 搜索采样模块
为了从总体分布中采样, 对策略添加正负对称的参数噪声
式中: δ表示均值为零的高斯向量; v为噪声方差。需要注意的是, 在动作噪声的作用下, 每次输入相同状态而得到的输出结果都不同。但本文中参数噪声在每个采样回合开始之前添加到当前策略参数中。因此, 在同一个采样回合中, 策略是确定的, 即多次输入相同的状态会得到相同的结果, 从而保证了策略在同一回合中的稳定性[21]。
每次采样时先在n个方向进行随机正负参数扰动, 从而获得2n个回合的采样结果。然后对这些采样结果的奖励值进行比较和排列, 并选择奖励相对较大的k组数据来更新策略。通过筛选相对较好的数据, 能够提高探索的效率, 避免了当回合奖励较小时, 无论朝着哪个方向更新都无法改善策略的情况发生。在此基础上, 进一步构建了搜索采样模块, 策略参数扰动过程表示为
式中: rmax为目前获得的最大回合奖励值; rt为当前策略奖励值; ε为设置的阈值。如果经过策略更新后, 发现回合奖励有显著提升且超过了设定的阈值, 那么在下次探索中保持探索方向不变, 并调整噪声方差, 以生成新的探索策略进行采样和策略更新。如果当前方向无法进一步改进策略时, 则产生新的扰动方向进行探索, 但保持噪声方差不变。这个过程实质上是根据探索经验指导下一步的探索方向, 通过对同一方向进行多次变步长探索, 以提高探索的效率。
2.3 新颖度引导复合更新模块
为了鼓励智能体进行探索并访问新的状态空间, 本文引入新颖度的概念, 以防止过早陷入局部最优解。在每个回合中, 设计了特征参数b(πi)以表示策略πi的特点。在本算例中, 可以使用回合结束时间Tf描述各个策略, 并记录每次采样得到的特征参数, 形成一个特征参数集合 A。当前策略的新颖度值N(b(πθ), A)通过计算当前策略πθ的特征参数b(πθ)与集合 A中随机抽取s个先前策略特征参数之间的平均距离获得, 即
新颖度值N(b(πθ), A)能够量化当前策略与过去策略之间的差异程度, 进而激励智能体更加积极地探索未知的状态空间。较大的新颖度值表示相对于之前的探索策略, 当前策略的探索能力更强。随着更多特征参数被添加到集合中, 探索策略的新颖度提升速度会变缓, 策略的新颖度会降低。通过优化新颖度值, 能够引导策略朝向未探索的行为空间进行调整, 从而实现更充分探索。基于策略新颖度的参数更新表示为
通过上述公式更新当前策略参数, 鼓励产生不同的行为策略, 使得策略参数向具有高新颖度的参数空间区域移动, 从而增加策略的新颖度。
然而, 奖励值可以直接反映策略的收益, 完全放弃基于奖励值的更新会导致数据利用效率降低。因此, 在策略更新过程中, 本文将新颖度引导的更新方法与有限差分方法相结合。为了充分发挥它们各自的优势, 引入权重值来对这2种更新方式进行加权, 并动态调整策略更新梯度的优先级。这样可以在更新过程中综合考虑新颖度和奖励值, 以实现更有效的策略更新。此时策略更新可以表示为
式中: ‖·‖2为二范数; ω表示自适应权重值, ω∈(0, 1)。在学习过程中, 权重值可以自适应地增加或减少。通过设置奖励阈值, 当奖励激励策略不断获得更优结果(奖励提升大于阈值)时增加奖励激励更新的比重。这意味着奖励值对策略更新的影响更大, 以便进一步提高策略的性能。然而, 如果在一定次数的更新后无法获得更优的策略或陷入局部最优解中(奖励提升始终小于阈值), 增加新颖度激励更新的权重。这样可以鼓励策略朝着具有更高新颖度的参数空间前进, 尝试更多不同的策略行为, 以克服局部最优解的困境。
通过2种更新方式的自适应切换, 既能够更好地探索未知领域, 又能够获得高回报的策略。奖励值可以直接反映策略的收益, 因此, 在训练结束后返回平均情景奖励最高的策略, 以保证获得最优的策略。算法流程如图 4所示。
 |
图4 A-ARS算法流程图 |
3 数值仿真验证与分析
数值仿真中假设航天器与非合作目标均在近地轨道附近且为短距离拦截任务, 考虑到燃料消耗相对于航天器以及非合作目标的质量而言可以忽略不计, 因此本文假定整个机动过程中航天器、非合作目标质量不变。传统方法基于策略最优必要条件和瞬时信息完全已知的假设对问题进行求解, 本仿真中将对满足必要条件和不满足必要条件的情景分别进行仿真分析。设参考轨道为600 km, 地球引力常数μ=3.986×105 km3/s2, 追踪航天器加速度约束aP=0.8 m/s2; 逃逸航天器加速度约束aE=0.3 m/s2; 追踪航天器的最大捕获半径Rmax=2 m; 行为空间分别为αi∈[-π/2, π/2], βi∈[-π/2, π/2];选取追踪航天器与目标航天器相对状态量为状态空间
在状态观测值的基础上, 在决策时位置和速度状态值上添加均值为0, 方差为3的高斯噪声; 为了进一步处理观测值并构造特征, 本文使用高斯函数作为基函数进行特征构造。具体而言, 可以对状态进行高斯平滑处理, 对每个状态值施加高斯函数的权重构造特征。这样做可以使观测值在不同状态下的变化更加平滑, 并将其转化为一组可供学习的特征。通过简化问题的复杂性, 提取出对问题求解有用的特征, 可以帮助智能体更好地理解状态空间, 更有效地学习策略。特征构造表示为
式中: μ为均值, 设为0;σ为标准差, 设为4;宽度为20。设计每回合最大时间tfmax=70 s。每回合奖励函数设计为
式中: R为结束时刻相对距离; ΔR为相邻时刻相对距离差值: ΔR=Rt-Rt-1; T为本次回合结束时间。仿真中出现以下3种情况则循环结束:
1) 在给定时域内, 仍未满足精度要求, 则该次循环结束;
2) 相对距离向量的二范数小于追踪航天器的最大捕获半径, 即表示成功拦截, 则该次循环结束;
3) 逃逸航天器和追踪航天器相对距离变大则该次循环结束。
为了验证算法的有效性和先进性, 以体现其性能, 对A-ARS算法、ARS算法、近端策略优化算法(proximal policy optimization, PPO)[22]和深度确定性策略梯度下降算法(deep deterministic policy gradient, DDPG)[23]进行了对比。在强化学习领域中, ARS和A-ARS算法都属于无梯度优化的非神经网络策略算法, 而PPO和DDPG分别是采用策略梯度下降更新的随机策略和确定性策略算法。使用算法对相同工况进行自主学习, 即S=[-5 000, 600, 0, 100, -6, 0], 并假设2个航天器的博弈策略满足最优必要条件。最后记录了奖励值的变化和更新次数, 并对追逃博弈的结果进行比对。仿真采用配置为2.3 GHz, CPU为i5-6300HQ, 8GRAM的计算机, 仿真编译环境采用Pycharm软件, 仿真步长0.1 s。
A-ARS和ARS算法的超参数设置为: 策略矩阵的初始值为一个6×2的随机初始化矩阵, 随机搜索方向的数量为20, 学习率为0.1, 更新样本的数量为10。A-ARS算法中, 探索阈值设置为0.1, 权重的初始值为0.5, 权重变化步长为0.1。PPO算法的超参数设置为折扣因子0.9, 批样本数量为30, critic网络的学习率为0.000 05, actor网络的学习率为0.000 1。DDPG算法的超参数设置为折扣因子0.9, 批样本数量为30, critic网络的学习率为0.000 2, actor网络的学习率为0.000 1。在DDPG和PPO算法中, 神经网络的隐藏层激活函数均选择了tanh函数。神经网络的具体设计如表 1所示。
强化学习算法的学习效果对比如表 2所示, 奖励值的累积变化如图 5所示。PPO和DDPG算法的采样回合和更新次数都多于其他算法, 但是策略效果提升缓慢。在该工况下控制量与距离变化如图 6~7所示。两者学到策略产生的控制量相对稳定, 变化较小, 这可以归因于在稀疏奖励环境中缺乏足够且有效的驱动数据, 无法计算梯度和更新策略参数, 无法有效探索新的行为空间和状态空间。因此, 深度强化学习算法的梯度下降优势无法充分发挥, 导致神经网络的收敛速度缓慢。
相比之下, ARS和A-ARS算法作为无梯度算法在该稀疏奖励问题中获得的奖励值增长更为显著, 策略的改进效果更好。可以看出相对于A-ARS算法, ARS算法由于缺乏有效的探索机制, 学习速度较慢。在前40次学习中, 策略改进效果明显, 但之后策略未能取得显著改善, 陷入了局部最优解, 无法有效地探索新的策略行为。学习结束时, ARS算法学习得到的策略与博弈成功的最小距离为39 m, 这超过了追踪航天器博弈成功的最小距离, 说明学习过程中未能稳定收敛到可行的策略。与此相反, A-ARS算法在经过80次学习更新后, 策略的改进稳定收敛, 并成功完成追踪任务。学习结束时, A-ARS算法的最小距离为0.05 m。这表明该算法在学习过程中能够稳定地收敛, 并成功找到了可行的策略。
在该工况下A-ARS算法的奖励值随学习次数的累积和权重值变化情况如图 8所示, 权重值自适应变化过程表明在学习过程中探索与奖励激励策略更新的方法交替进行。初始权重为0.5, 表示对探索和奖励激励策略更新的权重相同。然而, 由于初始时刻的快速策略效果提升, 有限差分方法开始更新策略参数的权重。随着学习的进行, 当策略在经过80个回合后逐渐稳定, 无法获得更高奖励值或更优策略时, 新颖度更新的权重值逐渐增加, 以鼓励探索新的参数空间。此外, 搜索采样模块的引入提高了探索效率, 使得A-ARS算法在更少的更新次数和采样回合的条件下能够更快地提升策略效果。
拦截博弈过程中轨迹变化如图 9所示, 行为控制量和相对距离相对速度分别如图 10和图 11所示。在一定初始距离下, 逃逸航天器采取逃逸策略, 追踪航天器朝着逃逸航天器方向逼近。随着追逃博弈的进行, 追踪航天器合理利用推力优势, 相对逃逸航天器速度越来越大, 两航天器之间的相对距离逐渐减小。在45 s时, 追踪航天器与逃逸航天器距离小于Rmax, 博弈结束。经过对比仿真, 验证了A-ARS算法相比于ARS、PPO及DDPG算法,极大地改善了策略学习效果, 具有明显的学习效率优势。仿真结果表明, 在一定工况下在经过自主学习后, A-ARS相对于其他强化学习算法能够更快地学习可行策略, 与非合作目标实现空间交会, 成功完成追逃博弈。综上所述, A-ARS算法相对于其他算法在此稀疏奖励问题中表现出更好的策略改进效果。
现实场景中, 由于受到太空环境、测量设备、导航方法以及天地通信能力的影响, 尤其是对于速度的测量存在误差, 可能会对求解结果产生影响。为了测试算法的鲁棒性和噪声对求解策略的影响, 选取初始状态S=[-5 000, -200, 0, 100, 6, 0], 在仿真的每一维状态值上分别添加均值为0, 方差1~4的高斯噪声, 每组方差间隔0.5, 并对已经收敛的策略在该初始状态下进行100次重复实验, 将误差分布绘制在图 12中。通过观察图 12可以发现, 当噪声为0时, A-ARS算法求解的策略最终距离为0.3 m。随着噪声的增加, 最终的误差也逐渐增大, 尤其是在方差为2.5之后, 误差增加明显, 特别是对极值的影响更为显著。然而, 由于强化学习算法直接与环境进行交互, 并对观测值进行特征构造处理, 它减小了噪声对策略效果的影响。在这个过程中, 速度分量相对于位置分量更容易受到初始噪声扰动的影响, 但最终对结果的误差影响非常小。均值相对来说都很好地保持在一定的误差范围内, 即使在方差最大为4的情况下, 所求得的解仍然能够满足追逃博弈成功的条件。这证明了该方法具有较好的鲁棒性。
为测试算法在不同工况学习求解能力和稳定性, 假设航天器初始位置在一定范围内随机分布, 如表 3所示, 采用A-ARS和ARS算法在随机初始位置条件下做200次重复实验, 得到结果如表 4所示。可以看出, 在初始位置随机变化时, 利用A-ARS算法学习求解, 可以实现高效拦截: 所有的轨迹均满足约束条件, 最终的相对距离也符合精度要求。而在同样的初始条件范围内ARS算法成功率只有64%, 证明前者对搜索采样和自适应更新的改进有效提升了算法的收敛能力和应对不同工况下学习能力。
传统的方法主要基于完全信息假设进行计算并且需要事先装订, 而在实际的追逃博弈中, 状态观测值存在噪声干扰, 两航天器并不知道对方的策略支付函数, 属于不完全信息博弈, 该方法缺乏灵活性[19]。而强化学习可以通过交互对策略参数进行调整, 使策略模型逐渐适用于当前的环境。针对逃逸航天器策略不满足最优博弈必要条件的情况, 在S=[-5 000, -200, 0, 100, 6, 0]工况下设计逃逸航天器的随机策略uE=k·uP, 其中k∈(0, 1)且在每一工况中随机产生, 仿真100次, 结果如表 5所示。
传统方法需要假定双方策略信息(如支付函数)和瞬时状态信息完全已知, 在强化学习中逃逸航天器的逃逸策略在博弈中通过状态观测值可以间接体现, 而强化学习是直接根据状态转移和奖惩值学习策略, 减少了对已知先验信息的依赖。针对仿真设计的随机逃逸策略, 对求解结果所需博弈时间影响小于1 s, 结果证明即使存在方差且对逃逸航天器策略不可知的非完全信息条件下也可以与环境交互获得可行的博弈策略。这进一步证明了强化学习的优势, 以及其在处理现实场景中复杂问题时的潜力。
经仿真比对, 本文采取的A-ARS算法提高了对数据的利用效率, 相对其他强化学习算法, 避免了智能体过早陷入局部最优, 能更快地学习到更优的策略, 采用神经网络的强化学习算法, 通过与巨大的状态空间和行为空间探索学习, 虽然可以在线决策, 但对数据有大量需求; 相比于传统的航天器追逃博弈求解, 强化学习直接与博弈环境交互, 减少了对博弈先验信息的依赖, 证明观测值的噪声干扰对求解影响较小, 能够有效解决航天器与非合作目标在非完全信息条件下追逃博弈问题, 更符合实际博弈场景。
策略和价值神经网络结构
算法学习效果对比
 |
图5 平均奖励曲线 |
 |
图6 控制量随时间变化曲线 |
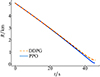 |
图7 距离随时间变化曲线 |
 |
图8 奖励值与权重值变化曲线 |
 |
图9 追踪与逃逸航天器轨迹随时间变化曲线 |
 |
图10 控制量随时间变化曲线 |
 |
图11 追逃航天器相对距离和相对速度随时间变化曲线 |
 |
图12 高斯噪声影响下误差分布 |
追踪航天器和目标的初始相对状态
不同初始位置下仿真结果
非最优博弈策略仿真结果
4 结论
本文针对生存型微分对策问题, 考虑强化学习稀疏奖励环境和探索困境, 设计了A-ARS算法。主要结论如下:
1) 基于增强随机搜索算法设计了搜索采样和自适应更新模块, 在稀疏奖励环境中稳定学习并且避免过早陷入局部最优。通过使用自适应增强随机搜索, 能够有效地应对追逃过程中存在的复杂非线性关系, 并实现对稀疏奖励任务的优化。
2) 利用微分策略最优控制必要条件辅助策略迭代, 进行算法测试后实验结果表明A-ARS算法相比ARS、PPO算法有更好的训练表现。
3) A-ARS采取线性策略形式而非神经网络策略, 放弃了神经网络更精确的拟合能力, 同时也减少了策略参数学习所需的数据量和学习时间需求, 具有简单有效、训练优化速度快等优点, 优于传统的强化学习方法, 在稀疏奖励环境中可以更快学习和收敛。
4) 强化学习直接与环境交互减少了对先验信息的依赖, 并且对观测值噪声干扰有一定的抵抗能力, 可以直接与环境交互学习而不需要初始值。
5) 通过仿真实验验证了构建线性策略的可行性, 具有策略形式简单, 节省计算资源, 数据利用效率高, 搜索学习能力更强的优势, 为生存型微分对策问题的解决提供一种新思路。
References
- RUMFORD T E. Demonstration of autonomous rendezvous technology(dart) project summary[J]. Space Systems Technology and Dperations, 2003, 5088: 10–19. [Article] [CrossRef] [Google Scholar]
- WEISMULLER T, LEINZ M. GNC demonstrated by the orbital express autonomous rendezvous and capture sensor system[C]//Proceedings of the 29th Annual AAS Guidance and Control Conference, 2006 [Google Scholar]
- LI Zhenyu, ZHU Hai. Survey on spacecraft orbital pursuit-evasion dferental games[J]. Scientia Sinica Technologica, 2020, 50(12): 1533–1545. [Article] (in Chinese) [CrossRef] [Google Scholar]
- YU Dateng, WANG Hua, ZHOU Wanmeng. Anti-rendezvous evasive maneuver method considering space geometrical relationship[J]. Journal of National University of Defense Technology, 2016, 38(6): 89–94. [Article] (in Chinese) [Google Scholar]
- QIAN Xingfang, LIN Ruixiong, ZHAO Yanan. Missile flight mechanics[M]. Beijing: Beijing Institute of Technology Press, 2006 (in Chinese) [Google Scholar]
- LI Chaoyong. Study on guidance and control problems for tactical ballistic missile interceptor[D]. Harbin: Harbin Institute of Technology, 2008 (in Chinese) [Google Scholar]
- ISAACS R. Differential Games[M]. New York: John Wiley and Sons, 1965 [Google Scholar]
- INNOCENTI M A, TARIAGIA V. Game tharec stalegies for spaceraif endezvous and mofion synchronzalion[C]//AIAA Guidance, Navigation and Control Conference, 2016 [Google Scholar]
- BARCHAN R, GCHOSE D. An SDRE based difrenial game approach for maneuvering target in erception[C]//AIAA Guidance, Navigation, and Control Conference, 2015 [Google Scholar]
- LI Z Y, ZHU H, YANG Z. A dimension-eduction solution of fre-time diferential games for spacecraft ursuit-evasion[J]. Acta Astronautica, 2019, 163: 201–210. [Article] [CrossRef] [Google Scholar]
- LIU Yanfang. Research on end-game guidance law for interceptor missile based on differential game theory[D]. Harbin: Harbin Institute of Technology, 2014 (in Chinese) [Google Scholar]
- ZHU Q, SHAO Z J. Missile real-time receding horizon pursuit and evasion games guidance based on neural network[J]. Systems Engineering and Electronics, 2019(7): 1597–1605 [Google Scholar]
- CAO Lei. Key technologies of intelligent game confrontation based on deep reinforcement learning[J]. Command Information System and Technology, 2019, 10(5): 1–7. [Article] (in Chinese) [Google Scholar]
- CHUN X, ALFRIEND K T, ZHANG J, et al. Q-learning algorithm for pathplanning to maneuver through a satellite cluster[C]//AAS/AIAA Astro-Dynamics Specialist Conference, 2018: 218–268 [Google Scholar]
- LIU Bingyan, YE Xiongbing, GAO Yong, et al. Strategy solution of norn-cooperative target pursuit evasion game based on branching deep rein-forcement learning[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(10): 348–358. [Article] (in Chinese) [Google Scholar]
- WU Qichang. Autonomous planning of spacecraft pursuit-evasion maneuver trajectory based on artificial intelligence method[D]. Changsha: National University of Defense Technology, 2019 (in Chinese) [Google Scholar]
- WU Qichang, ZHANG Hongbo. Spacecraft pursuit strategy and numerical solution based on survival differential strategy[J]. Control and Information Technology, 2019(4): 39–43. [Article] (in Chinese) [Google Scholar]
- LIAO Tian. Research on control and solving method of pursuit-evasion game for spacecraft[D]. Harbin: Harbin Institute of Technology, 2021 (in Chinese) [Google Scholar]
- ANDRYCHOWICZ M, WOLSKI F, RAY A, et al. Hindsight experience replay[C]//30th Annual Conference on Neural Information Processing Systems, 2017 [Google Scholar]
- MANIA H, GUY A, RECHT B. Simple random search of static linear policies is competitive for reinforcement learning[C]//31st Annual Conference on Neural Information Processing Systems, 2018 [Google Scholar]
- CONTI E, MADHAVAN V, SUCH F P, et al. Improving exploration in evolution strategies for deep reinforcement learning via a population of novelty-seeking agents[C]//31st Annual Conference on Neural Information Processing Systems, 2018 [Google Scholar]
- GU Y, CHENG Y, CHEN C L P, et al. Proximal policy optimization with policy feedback[J]. IEEE Trans on Systems, Man, and Cybernetics: Systems, 2021, 52(7): 4600–4610 [Google Scholar]
- SILVER D, LEVER G, HEESS N, et al. Deterministic policy gradient algorithms[C]//International Conference on Machine Learning, 2014 [Google Scholar]
All Tables
All Figures
 |
图1 Hill坐标系 |
| In the text | |
 |
图2 航天器推力方向角 |
| In the text | |
 |
图3 有限差分法原理及ARS算法更新示意图 |
| In the text | |
 |
图4 A-ARS算法流程图 |
| In the text | |
 |
图5 平均奖励曲线 |
| In the text | |
 |
图6 控制量随时间变化曲线 |
| In the text | |
 |
图7 距离随时间变化曲线 |
| In the text | |
 |
图8 奖励值与权重值变化曲线 |
| In the text | |
 |
图9 追踪与逃逸航天器轨迹随时间变化曲线 |
| In the text | |
 |
图10 控制量随时间变化曲线 |
| In the text | |
 |
图11 追逃航天器相对距离和相对速度随时间变化曲线 |
| In the text | |
 |
图12 高斯噪声影响下误差分布 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


