| Issue |
JNWPU
Volume 42, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 108 - 116 | |
| DOI | https://doi.org/10.1051/jnwpu/20244210108 | |
| Published online | 29 March 2024 | |
Optimizing and designing upper-stage separation spring of lifting-body rocket
升力体火箭上面级分离弹簧优化设计研究
Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China
Received:
23
February
2023
Because the upper-stage separation of a lifting-body rocket is difficult under the low-altitude and high-speed flight environments, an upper-stage separation scheme based on the separation spring is proposed. The integration of ADAMS and MATLAB realizes the multi-body dynamics simulation analysis of upper-stage separation. The experimental design method is used to carry out the target simulation and calculation of the upper-stage separation process, with the separation condition deviation and the separation spring deviation considered at the same time, thus ensuring the reliability of the separation scheme. In order to further optimize the separation scheme, an upper-stage separation optimization model is established with the Isight software, and the mass of separation spring is optimized with the multi-island genetic algorithm and significantly reduced by 48.87% under the condition that the upper-stage separation process satisfies all constraints, thereby effectively improving the performance of the lifting-body rocket.
摘要
针对升力体火箭在低空高速飞行环境下上面级分离难度大的问题, 提出了一种基于分离弹簧的上面级分离方案, 将ADAMS和Matlab集成实现了分离多体动力学仿真分析, 采用试验设计方法对同时考虑分离工况偏差和分离弹簧偏差的上面级分离过程进行打靶仿真计算, 确保了分离方案的可靠性。为了进一步优化分离方案, 基于Isight建立了上面级分离优化问题模型, 并采用多岛遗传算法对分离弹簧质量进行了优化设计, 在确保分离过程满足全部约束条件的情况下使分离弹簧质量大幅降低, 其降幅达到了48.87%, 有效提升了火箭性能。
Key words: upper-stage separation / separation spring / dynamics simulation / target simulation / design optimization
关键字 : 上面级分离 / 分离弹簧 / 动力学仿真 / 打靶仿真 / 优化设计
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
运载火箭的分离运动是一个复杂的高速多体运动学过程,近几十年来各国火箭型号由于分离出现问题导致飞行失败的情况并不少见,故分离是运载火箭执行任务中至关重要的一环,分离方案的可靠程度以及分离装置的性能将直接决定发射任务成败[1]。
运载火箭上面级分离一般为冷分离,升力体火箭为了充分利用分离前体的升力体构型产生的高升阻比特性,分离高度较低、动压较大,分离过程中气动特性相对复杂,在下面级助推器的影响下分离难度更大,往往需要依靠分离弹簧等分离能源辅助前后体安全分开[2]。分离弹簧作为一种常用的分离能源,优势在于不需要火工品,分离可靠性高,但其在分离过程中产生的分离力会同时作用在前后体上,进而同时影响前后体的相对位置和姿态,故分离弹簧的性能参数对分离可行域和适应边界影响较大[3]。
近年来国内外对分离动力学过程和分离弹簧作用影响展开研究,Christensen等[4]完成了分离动力学分析综述,对各类分离动力学问题进行了归纳总结; Chao等[5]对基于分离弹簧的有效载荷卫星释放过程进行了分析,重点研究了分离对卫星相对运动和姿态的影响;Shiell等[6]研究了分离弹簧将有效载荷模块从某航天器中分离的过程,分析满足最小分离速度、最小姿态扰动等约束条件,并确保分离体间不发生干涉碰撞;Liu等[7]对航天器分离弹簧进行了优化设计,以最小体积为优化目标,在确保性能参数满足要求的情况下实现体积有效降低;袁勇等[8]对采用4根分离弹簧的小卫星分离过程进行了分析,重点考虑了弹簧作用点、推力线、不同步性等偏差干扰因素,获得了不同影响因素对分离精度的敏感程度及相互关系。本文针对某升力体火箭在低空高速飞行环境下的上面级分离问题开展研究。首先基于ADAMS和Matlab的多体动力学联合仿真分析完成了上面级分离方案设计,明确了分离弹簧的初始性能参数和安装位置,同时在仿真分析过程中引入了火箭各项偏差干扰,并通过试验设计完成了打靶仿真,确保在偏差干扰下也能够安全分离。之后为了进一步提升火箭性能,以分离弹簧质量最小为目标,基于Isight建立了上面级分离优化问题模型,采用多岛遗传算法对分离弹簧性能参数和安装位置进行了设计优化。最终在确保安全分离的条件下大幅降低了弹簧质量,相比初始状态降低了48.87%,从而实现了对火箭性能的提升。
1 上面级分离问题描述
在运载火箭研制中,分离技术的研究十分关键。本文研究的升力体火箭上面级分离采用冷分离方案,分离面设置在分离前体和分离后体的对接面,在对接面处安装4根分离弹簧辅助前后体安全分开。上面级分离前,火箭几何模型坐标系如图 1所示。
其中坐标原点O位于分离前体顶点偏上的位置;OX轴位于火箭纵向对称平面内,垂直于底部平面,与分离后体柱段轴线重合,从弹尾指向分离前体方向为正;OY轴位于火箭纵向对称平面内,垂直于OX轴指向上方为正;OZ轴垂直于OXY平面,正向满足右手定则。
分离前体底部存在突出物,其伸入分离面以下225 mm,故分离过程中需确保前后体轴向相对运动距离超过225 mm时不发生碰撞,将此作为安全分离的重要约束条件。上面级分离位置关系如图 2所示。
为了提升分离可靠性,在分离前体突出物左右两侧对称安装4个分离弹簧,如图 3所示。同时,由于分离前体为升力体构型,为了利于分离前体起控,需确保分离过程中不出现低头运动情况,即俯仰角增量大于0,故将分离弹簧布置在分离前体和分离后体质心偏下的位置,使其在分离过程中能够为分离前体提供抬头力矩。
确定分离弹簧初始性能参数如表 1所示。
分离弹簧机构由外套筒、内套筒、上顶板和弹簧组成[9],外套筒固定安装在分离后体的弹簧支架上,从而使分离过程中分离弹簧机构随分离后体运动,且与分离后体完全固连、无相对运动。尚未分离时,分离弹簧处于最大压缩状态,此时弹簧预紧力达到最大803 N。随着前后体逐渐分离,弹簧力逐渐释放,在弹簧作用下内套筒与上顶板向前伸出外套筒,并通过外套筒端口限位确保内套筒与外套筒的相对运动仅有一个(轴向)自由度。最终弹簧达到自由长度,弹簧推力完全释放,内套筒伸出长度达到最大[10]。分离弹簧机构的结构示意图如图 4所示。
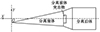 |
图1 坐标系示意图 |
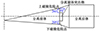 |
图2 上面级分离位置关系 |
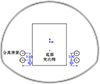 |
图3 分离弹簧安装位置 |
分离弹簧初始性能参数
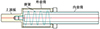 |
图4 分离弹簧结构示意图 |
2 多体动力学数学模型与仿真模型分析
2.1 分离数学模型
首先通过理论分析建立数学模型,对前后体的运动特性进行初步分析[11]。
由于上面级分离过程较复杂,在建立分离动力学的数学模型时进行适当简化,将前后体气动力简化为分离全程受到气动力的平均值,可使得理论分析结果与实际结果相差较小,分离过程中考虑了以如表 2所示的受力因素。
将前后体分离运动分解为:质心轴向相对运动、质心法向相对运动和前后体相对各自质心的转动运动。其中,分离弹簧推力作用点简化为分别作用于前后体质心[12]。
前后体法向运动和转动运动的微分方程如(1)式所示:
式中: m1, m2分别为分离前体和分离后体的质量; FN1, FN2分别为分离前体和分离后体受到的法向气动力; ΔH为前后体法向相对错动距离; θ1, θ2分别为分离前体和分离后体的俯仰角增量; J1, J2分别为分离前体和分离后体的转动惯量; Mz1, Mz2分别为分离前体和分离后体受到的气动力矩;
分离过程中, 后体碰撞危险点的运动情况可分解为: 后体质心在惯性坐标系下的平动运动与碰撞危险点相对后体质心转动运动的叠加,如图 5所示。
由图可见, 碰撞危险点在分离过程中的法向合位移Y=Y1+Y2, 代入前后体几何参数和气动力进行计算, 可获得碰撞危险点的法向合位移。联立公式(1), 并通过前后体几何参数转换, 即可分别求得分离前体和分离后体碰撞危险点的法向合位移, 从而求得分离间隙以及分离碰撞时间。
考虑分离弹簧工作情况时, 前后体轴向运动情况如(2)式所示, 令弹簧自由长度x0小于最小安全分离距离(225 mm), 当x < x0时根据受力分析得到
式中: a1, a2分别为分离前体和分离后体的轴向加速度; F弹为分离弹簧推力;FA1, FA2分别为分离前体和分离后体受到的轴向气动力; F后效为分离后体发动机后效力; k为弹簧刚度系数; x0, x分别为弹簧自由长度和前后体轴向分离距离。令
则
由(4)式可求出通解
当t=0时, x=0, ẋ=0, ẍ=c1a
联立可求得
当x=x0时, 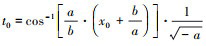 , t0为弹簧达到自由长度时经历的时间。
, t0为弹簧达到自由长度时经历的时间。
当x>x0时, 分离弹簧已不再继续做功, 该状态下根据受力分析得到(8)式
联立求解可得到
式中, 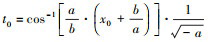 ,
, 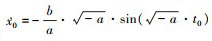 。
。
此时该方程为前后体轴向分离距离x与弹簧刚度系数k、弹簧自由长度x0、分离时间t有关的函数。因此, 当分离弹簧性能确定时, 即可获得轴向相对分离距离、分离间隙随分离时间t的变化情况。
对于本文上面级分离方案, 将分离弹簧的刚度系数和自由长度代入公式, 计算得到当前后体轴向分开225 mm时, 分离时间为0.192 s, 最小分离间隙为184.61 mm。因此, 通过建立数学模型进行理论计算可获得结论: 上面级可以实现安全分离, 且分离间隙余量较大。
上面级分离受力因素
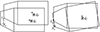 |
图5 后体碰撞危险点运动示意 |
2.2 分离仿真模型
为了建立更加准确预示分离过程的精细化模型, 本文联合多种软件对整个分离过程进行多体动力学仿真分析[13]。首先采用CATIA进行三维精细化建模, 将模型导入到ADAMS中进行多体动力学仿真分析, 之后完成ADAMS与Matlab的输入输出接口设置, 通过Matlab实现气动数据插值, 并利用simulink完成ADAMS多体动力学分析模块与气动数据插值模块的集成, 实现数据传递。ADAMS和Matlab进行联合仿真流程如图 6所示。
如流程图所示, 根据初始分离姿态, 得到分离起始时刻的气动特性。将气动特性传入ADAMS多体动力学求解模块, 获得下一迭代步两体姿态和位置的变化情况, 之后将该变化情况传回Matlab气动插值程序获得下一迭代步的气动特性。如此反复进行迭代计算, 直到两体的分离距离满足分离要求, 则分离仿真结束。
上面级分离过程中, 分离弹簧推力同时作用在分离前体和分离后体上, 由于分离前体和分离后体质量特性存在差异, 在弹簧推力作用下前后体存在相对姿态转动, 从而使弹簧的推力作用点在分离过程中不断移动。故仿真模型中除弹簧轴向推力外, 还需要考虑弹簧推力作用点在分离前体底部移动产生的摩擦力[14]。
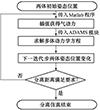 |
图6 ADAMS与Matlab联合仿真流程图 |
2.3 分离仿真分析结果
对基于分离弹簧的上面级分离过程开展仿真分析。仿真初始条件为: 分离动压3 000 Pa, 分离攻角2°, 分离过程中后体发动机后效力取400 N。本文取分离前体起控时刻为上面级分离后0.5 s, 在标准分离条件下, 分离0.5 s时轴向分离距离为531.7 mm, 分离过程中最小分离间隙为173.2 mm, 分离后体脱离分离前体突出物包络时间为0.215 s。分离仿真情况如图 7~9所示。可以看出, 前后体能够安全可靠分离, 该仿真计算结果与2.1节理论推导结果较为接近, 偏差不超过10%, 能够验证理论分析的正确性, 较小的差异主要在于理论推导中将前后体气动力简化为分离全程受到气动力的平均值, 以便于推导计算。
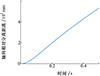 |
图7 轴向相对分离距离 |
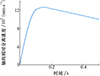 |
图8 轴向相对分离速度 |
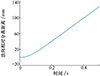 |
图9 法向相对分离距离 |
3 偏差试验设计打靶仿真
3.1 上面级分离偏差项
实际分离过程中, 分离工况不会像标准状态那么理想, 存在大量偏差干扰, 使得上面级分离风险增大。为了验证分离方案的适应能力和可靠性, 确保其在各极限偏差条件下也能安全分离, 采用DOE screening design(2 level)方法获得各极限偏差组合下的设计矩阵, 对各偏差条件下分离过程进行打靶仿真分析。对分离过程影响较大的偏差为: 前后体气动力偏差、后效力推力偏差、质心位置偏差、质量偏差、转动惯量偏差[15]。基于该背景火箭研制情况, 并参考规模相近火箭的设计情况, 各偏差项偏差取值见表 3。
除分离工况偏差外, 分离弹簧在安装和工作过程中也会产生偏差, 对分离前体起控姿态和分离间隙产生干扰, 故也需要对分离弹簧的安装位置偏差、性能偏差以及不同步性导致的推力偏差进行分析。根据航天工业部部标准QJ 1787-89, Ⅱ类弹簧推力极限偏差不超过10%;根据生产误差及装配工艺, 弹簧安装位置偏差不会超过5 mm, 为便于分析其影响程度, 将弹簧推力位置偏差适当扩大至10 mm进行分析, 故打靶仿真中考虑的分离弹簧各偏差项及其上下限如表 4所示。
基于表 3和表 4的所有偏差项, 在ADAMS中建立考虑偏差干扰下的分离仿真模型, 对该模型进行打靶仿真分析。
分离工况偏差项情况
分离弹簧偏差项情况
3.2 打靶仿真分析结果
采用DOE screening design(2 level)方法针对各偏差项选取256个试验设计状态, 并进行256次打靶仿真。其所有设计参数均取上下边界值, 进行交叉组合并生成设计矩阵[16], 基于设计矩阵完成打靶仿真计算和结果分析, 打靶仿真结果如图 10~12所示。
根据仿真结果, 分离0.5 s时前后体轴向相对分离距离范围为470~580 mm, 轴向相对分离速度范围为840~1 100 mm/s, 最小分离间隙范围为140~195 mm, 所有偏差组合工况下前后体均能实现安全分离。
可以看出, 根据打靶仿真结果, 考虑不同极限偏差组合干扰下, 前后体依然能够实现安全分离, 且仍有一定分离裕度。因此, 该分离弹簧方案可以满足上面级分离需求, 且存在进一步优化的余量。
 |
图10 轴向相对分离距离(打靶) |
 |
图11 轴向相对分离速度(打靶) |
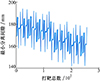 |
图12 最小分离间隙(打靶) |
4 上面级分离优化设计
火箭运载能力对火箭结构质量十分敏感, 为了最大化确保火箭运载能力, 火箭结构质量需尽量降低。对于总质量相对较轻的火箭, 仅减重几公斤即能够对火箭运载能力有明显提升。因此, 需要对分离弹簧进行优化设计, 使其质量最好。
4.1 优化问题描述
为了使火箭性能更优, 将分离弹簧质量M最小作为该上面级分离优化问题的目标函数。设计变量一般选取能直接反映分离运动特性的参数, 对于该优化问题, 分离弹簧推力和刚度系数直接决定了弹簧质量大小和分离速度快慢, 分离弹簧安装位置则直接决定了分离体姿态变化情况和分离间隙大小, 故选择分离弹簧初始推力F、分离弹簧刚度系数k以及4个分离弹簧法向安装位置y1, y2, y3, y4作为设计变量。上面级分离过程间隙需留有一定余量, 且前后体需具有较大相对分离速度, 使拉开安全距离所需时间较短, 确保分离前体尽早起控。因此, 该优化问题约束条件设置为: 前后体分离过程中最小分离间隙d不小于50 mm, 确保分离安全, 无碰撞风险; 前后体分离至安全距离所需时间t不超过0.4 s, 确保前后体快速分开, 缩短上面级起控时间; 前后体分离至安全距离(分离前体起控)时分离前体俯仰角增量Δψ大于0°, 确保分离过程中上面级为抬头运动趋势, 有利于升力体上面级可靠起控。上面级分离优化问题的数学模型为
上面级分离优化设计的初始条件与2.3节一致, 根据3.2节不同偏差项组合下的上面级分离偏差打靶仿真结果, 可以获得最不利于分离的偏差项组合及其取值情况, 即: 气动力取上偏差, 后效力取上偏差, 分离前体和分离后体质量取上偏差, 分离前体质心纵向偏差取上偏差, 分离前体质心法向偏差取下偏差, 分离后体质心纵向偏差取下偏差, 分离后体质心法向偏差取上偏差, 分离前体转动惯量取上偏差, 分离后体转动惯量取下偏差。基于该极限偏差工况和初始分离条件, 对上面级分离进行优化设计, 其中设计变量参数初始值如表 5所示, 约束条件和目标函数初始值如表 6所示。
设计变量初始状态
约束条件和目标函数初始状态
4.2 优化框架
本文采用Isight商用软件搭建分离优化问题框架[17], 搭建的优化流程如图 13所示。
上面级分离优化框架由优化模块、多体动力学计算模块和参数求解模块组成。首先通过多体动力学计算模块实现整个分离过程的仿真计算, 之后通过参数求解模块将分离仿真结果转换为优化所需的约束条件和目标函数, 最终通过优化模块实现对分离问题的优化分析, 在不断迭代计算中使目标函数逐渐逼近最优解。
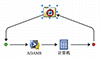 |
图13 上面级分离优化框架 |
4.3 优化结果
分离多体动力学求解速度较快, 分析成本较低, 能够满足较多样本点数的求解需求, 因此针对上面级分离优化问题采用多岛遗传算法进行优化设计, 控制参数设置为: 岛数为5, 子种群规模为50, 进化代数为10, 交叉概率为0.8, 变异概率为0.01, 移植概率为0.01。优化过程共迭代2 501步, 第2 385步获得最优解, 优化后的分离弹簧最小质量为0.308 33 kg, 相比初始状态有了显著降低, 其降幅达到48.87%。分离弹簧质量优化历程如图 14所示。
最小分离间隙、分离时间和分离前体俯仰角增量随着优化的进行逐渐趋于收敛, 如图 15~17所示。优化达到最优点时最小分离间隙降至131.95 mm, 分离时间增大至0.399 s(已接近0.4 s边界), 分离前体俯仰角增量降至0.071°(已接近0°边界), 所有约束条件均收敛至边界范围以内, 且分离时间和分离前体俯仰角增量均接近约束边界。可以看出, 此时已基本没有进一步优化的空间。
分离弹簧质量优化达到最小值时, 其弹簧初始推力为655.765 N、弹簧刚度系数为7.462, 对应的弹簧长度工作行程约为87.88 mm, 相比优化前状态171 mm的工作行程和803 N的初始推力均有显著降低。4个分离弹簧法向安装位置y1, y2, y3, y4优化后分别为-98, -45, 24, -42 mm。可以看出, 分离弹簧法向安装位置在优化后相比初始状态(0, 0, 50, 50)mm均有一定程度下移, 说明在弹簧推力和弹簧工作行程减小时, 通过适当下移分离弹簧的安装位置可确保为上面级提供抬头力矩, 以满足起控时分离前体俯仰角增量大于0°的约束条件。分离弹簧推力、刚度系数的优化收敛历程如图 18~19所示。
因此, 上面级分离方案经过优化设计后, 分离弹簧质量显著降低, 且约束条件均能满足分离需求, 火箭总体性能得到有效提升。
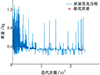 |
图14 分离弹簧质量优化历程(目标函数) |
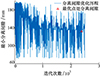 |
图15 最小分离间隙优化迭代 |
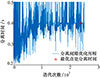 |
图16 分离时间优化迭代历程(约束条件) |
 |
图17 分离前体俯仰角增量优化迭代历程(约束条件) |
 |
图18 分离弹簧推力优化迭代历程(设计变量) |
 |
图19 分离弹簧刚度系数优化迭代历程(设计变量) |
5 结论
本文以升力体运载火箭作为研究背景, 对基于分离弹簧的上面级分离方案进行了仿真分析和优化设计, 取得的研究成果为:
1) 完成了基于分离弹簧的上面级分离初始方案设计, 形成了满足升力体火箭分离和起控约束的分离方案, 通过理论推导和数值模拟验证了方案的正确性, 计算偏差不超过10%。
2) 建立了考虑不同偏差干扰下的上面级分离打靶仿真模型, 对分离过程进行了打靶分析, 结果表明考虑多种偏差干扰因素后, 仍能够满足升力体火箭分离和起控要求, 且该方案具有进一步优化的空间。
3) 为使火箭性能更优, 以分离弹簧质量最小为目标, 采用多岛遗传优化算法对上面级分离初始方案进行了优化设计, 针对升力体火箭特征建立了满足升力体上面级分离和起控需求的优化问题数学模型, 最终在满足约束条件的情况下使分离弹簧质量降低了48.87%, 获得了较好的优化效果。
References
- GUO Tiancheng. Dynamics of multi-warhead separation process in high speed aerodynamic environment[D]. Harbin: Harbin Institute of Technology, 2019 (in Chinese) [Google Scholar]
- QIAN Cheng, WANG Xiaohui, ZHANG Haizheng, et al. Simulation and analysis of rigid-flexible coupling for stage separation of missile based on ADAMS[J]. Journal of Ordnance Equipment Engineering, 2017(4): 77–81. [Article] (in Chinese) [Google Scholar]
- GU Mingkun, HE Wei, TANG Ke, et al. Research on the development plan of Chinese liquid launch vehicle structure system[J]. Astronautical Systems Engineering Technology, 2021, 5(2): 55–67. [Article] (in Chinese) [Google Scholar]
- CHRISTENSEN K L, NARAHARA R M. Spacecraft separation[J]. Space Aeronuatics, 1996, 46: 74–82 [Google Scholar]
- CHAO J, WANG Z, ZHANG Y. Development of the new approach of formation initialization using spring separation mechanism considering J2 perturbation[J]. Advances in Space Research, 2015, 55(11): 2616–2627. [Article] [CrossRef] [Google Scholar]
- SHIELL J, CANTY P, KILEY A, et al. Dynamic modelling of the bepi-colombo separation system: perturbation analysis of mass properties and separation spring parameters[C]//13th European Space Mechanisms and Tribology Symposium, 2009: 505–532 [Google Scholar]
- LIU Z J, ZHAO X Q, ZHANG J Y, et al. Spiral torsion spring optimization design for separation devices[J]. Journal of Donghua University(English Edition), 2016(2): 33 [Google Scholar]
- YUAN Yong, CHEN Hui, DU Shanliang, et al. Modeling and analysis on separation process for small satellite[J]. Flight Dynamics, 2019, 37(1): 4. [Article] (in Chinese) [Google Scholar]
- GUO Yongchang. Study on interstage scheme of solid launch vehicle considering residual thrust[D]. Harbin: Harbin Institute of Technology, 2017 (in Chinese) [Google Scholar]
- HURLEY M J, CARRIE G W. Stage separation of parallel-staged shuttle vehicles-A capability assessment[J]. Journal of Spacecraft & Rockets, 2012, 9(10): 764–771 [Google Scholar]
- RAO B N, JEYAKUMAR D, BISWAS K K, et al. Rigid body separation dynamics for space launch vehicles[J]. The Aeronautical Journal, 2016, 110(1107): 289–302 [Google Scholar]
- PAMADI B N, TARTABINI P V, TONIOLO M D, et al. Application of constraint force equation methodology for launch vehicle stage separation[J]. Journal of Spacecraft and Rockets, 2013, 50(1): 191–205. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- LI Yanjun. Co-simulation analysis of stage separation of missile based on FLUENT and ADAMS[D]. Harbin: Harbin Institute of Technology, 2012 (in Chinese) [Google Scholar]
- TIAN S, FU J, CHEN J. A numerical method for multi-body separation with collisions[J]. Aerospace Science and Technology, 2020, 109(3): 106426 [Google Scholar]
- ROSHANIAN J, TALEBI M. Monte Carlo simulation of stage separation dynamics of a multistage launch vehicle[J]. Applied Mathematics and Mechanics, 2008(11): 29 [Google Scholar]
- JUNG U H, KIM J H, KIM J H, et al. Optimum design of diffuser in a small high-speed centrifugal fan using CFD & DOE[J]. Journal of Mechanical Science & Technology, 2016, 30(3): 1171–1184 [CrossRef] [Google Scholar]
- LAI Yuyang. Isight parameter optimization theory and example explanation[M]. Beijing: Beihang University Press, 2012: 1–10 (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 坐标系示意图 |
| In the text | |
 |
图2 上面级分离位置关系 |
| In the text | |
 |
图3 分离弹簧安装位置 |
| In the text | |
 |
图4 分离弹簧结构示意图 |
| In the text | |
 |
图5 后体碰撞危险点运动示意 |
| In the text | |
 |
图6 ADAMS与Matlab联合仿真流程图 |
| In the text | |
 |
图7 轴向相对分离距离 |
| In the text | |
 |
图8 轴向相对分离速度 |
| In the text | |
 |
图9 法向相对分离距离 |
| In the text | |
 |
图10 轴向相对分离距离(打靶) |
| In the text | |
 |
图11 轴向相对分离速度(打靶) |
| In the text | |
 |
图12 最小分离间隙(打靶) |
| In the text | |
 |
图13 上面级分离优化框架 |
| In the text | |
 |
图14 分离弹簧质量优化历程(目标函数) |
| In the text | |
 |
图15 最小分离间隙优化迭代 |
| In the text | |
 |
图16 分离时间优化迭代历程(约束条件) |
| In the text | |
 |
图17 分离前体俯仰角增量优化迭代历程(约束条件) |
| In the text | |
 |
图18 分离弹簧推力优化迭代历程(设计变量) |
| In the text | |
 |
图19 分离弹簧刚度系数优化迭代历程(设计变量) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


