| Issue |
JNWPU
Volume 42, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 129 - 137 | |
| DOI | https://doi.org/10.1051/jnwpu/20244210129 | |
| Published online | 29 March 2024 | |
Unsupervised 3D reconstruction method based on multi-view propagation
基于多视图传播的无监督三维重建方法
1
School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
2
School of Cyber Engineering, Xidian University, Xi'an 710071, China
Received:
17
March
2023
In this paper, an end-to-end deep learning framework for reconstructing 3D models by computing depth maps from multiple views is proposed. An unsupervised 3D reconstruction method based on multi-view propagation is introduced, which addresses the issues of large GPU memory consumption caused by most current research methods using 3D convolution for 3D cost volume regularization and regression to obtain the initial depth map, as well as the difficulty in obtaining true depth values in supervised methods due to device limitations. The method is inspired by the Patchmatch algorithm, and the depth is divided into n layers within the depth range to obtain depth hypotheses through multi-view propagation. What's more, a multi-metric loss function is constructed based on luminosity consistency, structural similarity, and depth smoothness between multiple views to serve as a supervisory signal for learning depth predictions in the network. The experimental results show our proposed method has a very competitive performance and generalization on the DTU, Tanks & Temples and our self-made dataset; Specifically, it is at least 1.7 times faster and requires more than 75% less memory than the method that utilizes 3D cost volume regularization.
摘要
提出一种端到端的深度学习框架, 从多视图中计算深度图从而重建出三维模型。针对目前大多数研究方法通过3D卷积实现3D成本体积正则化并回归得到初始深度图带来巨大的GPU内存消耗, 以及由于设备受限导致有监督的方法中深度图真值难以获取的问题, 提出一种多视图传播的无监督三维重建方法。该方法借鉴Patchmatch算法思想, 在深度范围内将深度划分n层, 通过多视图传播得到深度假设, 并利用多个视图之间的光度一致性、结构相似性和深度平滑度构建多指标损失函数, 作为网络中学习深度预测的监督信号。实验表明, 文中提出的方法在DTU、Tanks & Temples和自制数据集上的性能和泛化性非常有竞争力, 比采用3D成本体积正则化的方法快1.7倍以上, 内存使用量减少75%。
Key words: multi-view propagation / unsupervised / 3D reconstruction / Patchmatch algorithm / multi-metric loss function
关键字 : 多视图传播 / 无监督 / 三维重建 / Patchmatch算法 / 多指标损失函数
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
三维重建技术作为计算机视觉领域的热门技术在医学治疗、航天航海、自动驾驶、VR虚拟现实等领域应用相较成熟, 一直受到大家重点关注。出于对重建成本和设备易得性考虑, 利用视觉传感器获得多张已知相机参数的不同视角图像重建出真实三维场景成为研究人员常用手段之一, 即多视图立体匹配(multi-view stereo, MVS)。尽管, MVS已经被研究了几十年, 但它仍面临一些挑战, 如遮挡、照明变化以及无纹理区域等问题使得MVS的实际应用更加具有挑战性。
随着深度学习的高速发展, 越来越多的研究人员将端到端的神经网络引入到MVS方法中, 将三维重建看作分类和回归问题, 从而利用神经网络在训练过程中得到的先验知识, 解决经典MVS模型无法解决的问题。2018年, Yao等[1]首次将深度学习引入到MVS方法中, 提出MVSNet, 其基于Plane-sweeping算法[2]和可微单应性变换构建3D代价体, 使用3D CNN对其进行正则化, 然后回归出深度图, 最后通过融合估计的深度图来获得3D几何体, 但3D CNN的使用需要消耗巨大的GPU内存。为此, R-MVSNet采用GRU时序网络以顺序方式正则化代价体[3], 以增加大量运行时间为代价, 减少了GPU内存需求。Yang等[4]提出了CVP-MVSNet, 采用从粗到细的网络构建代价体金字塔, 而不是像MVSNet方法一样以固定分辨率构建代价体, 与上述所提方法相比, 有着更加紧凑、轻量级的网络结构。这些通过构建代价体的方法虽然在重建质量上取得了不错的效果, 但在运行时间和消耗内存方面仍不令人满意。
几种传统的MVS方法[5-7]舍弃了构建代价体的思想, 基于Patchmatch算法思想, 消耗较少的内存就能完成深度图估计。Patchmatch算法最早于2009年由Barnes等[8]提出, 用于寻找图像块之间的近似最近邻匹配, 寻找最近邻的速度是一次质的飞跃。2011年, 文献[9]提出了Patchmatch Stereo算法, 其核心思想是基于迭代传播为所有的像素点分别找一个属于该像素的视差平面, 利用这个视差平面计算该像素点的视差值。2015年, Galliani等[5]提出了Gipuma算法, 该算法基于Patchmatch Stereo算法提出了一种新的、大规模并行的高质量多视点匹配方法, 它使用红黑棋盘模式并行化进行过程中的消息传递, 更适合多核GPU, 并从双目匹配扩展到多视图匹配。2016年, Schönberger等[6]基于Patchmatch算法提出了Colmap算法, 它联合逐像素视图选择、深度图和表面法线进行深度估计。2019年, Xu等[7]在Gipuma算法基础上, 提出了高效准确的ACMH算法, 效率是Colmap算法的8~10倍; 针对低纹理区域的深度估计, 他进一步提出了多尺度几何一致性引导框架(ACMM), 并将ACMH与ACMM相结合, 获得较粗尺度下低纹理区域可靠的深度估计值, 并确保其可以传播到更细尺度。
文献[10]结合深度学习和Patchmatch方法思想, 提出了PatchmatchNet算法, 它继承Patchmatch算法效率的同时, 也利用深度学习提高了性能。相比于3D CNN正则化3D代价体和GRU时序网络正则化2D代价图的方法, 运行速度快2.5倍以上, 内存使用量减少66.67%。然而, 这些方法虽然取得了不错的精度, 但依赖于3D地面真实数据的监督。
针对3D地面真实数据获取困难的问题, 不少研究人员开始研究无监督的MVS方法, 通过建立自我监督损失以估计该视图上重建的图像和真实图像之间的差异。Khot等[11]提出了基于鲁棒光度一致性的无监督MVS方法(Unsup-MVS), 为克服视图之间的遮挡和照明变化, 提出一种稳健的损失公式, 即强制执行一阶一致性和针对每个点选择性地强制执行与某些视图一致性的方法。Huang等[12]提出了一种新的无监督多度量MVS网络(M3VSNet), 提出一种新的多度量损失函数, 该函数结合了像素和特征损失函数, 以从匹配对应的不同视角学习固有约束。但是, 这些无监督MVS方法中大部分采用了经典的方法, 即采用3D CNN对3D代价体进行正则化并回归出深度图的方法, 耗费了大量的内存和时间。
针对上述问题, 借鉴PatchmatchNet方法, 本文提出一种基于多视图传播的无监督三维重建方法, 命名为Uns-PMVSNet, 改进了PatchmatchNet网络内部结构, 不用依赖于3D地面真实数据并使用较少的内存和较短的时间就能重建出较高质量的三维模型, 使网络的普适性得到大幅度提升。
1 Patchmatch算法理论
文献[9]提出Patchmatch方法核心思想是随机搜索和迭代更新, 主要包括4个步骤:①初始化:每个像素根据深度范围随机初始化相应的深度值; ②传播:把初始的所有深度平面内的正确的深度平面传播至同一深度平面内的其他像素, 迭代多次; ③匹配代价计算与聚合:计算每个像素不同深度估计的匹配代价, 选取代价最小的深度值作为深度估计值;④随机分配:在每次传播后, 对当前像素的平面在一定范围内随机生成一个调整量, 寻找代价最小的那个平面, 加快找到真实的平面。
基于Patchmatch算法思想,文献[10]提出了基于学习的Patchmatch方法, 即PatchmatchNet。该方法主要流程为: ①深度图初始化:借鉴Plane-sweeping算法[2]思想, 预定义深度范围为[dmin, dmax], 第一次迭代时, 在逆深度范围内对每个像素的深度假设采样48个间隔得到48个深度层, 这些深度层组成一个采样深度图; ②自适应传播:采用2D卷积学习每个像素p的K个邻域的额外偏移量, 然后根据这个偏移量得到自适应邻域的像素坐标, 将邻域对应的深度值传给中心像素作为中心像素的深度假设, 然后加上初始化得到的深度图为中心上下采样几层(局部扰动)后的深度假设作为新的深度假设; ③自适应匹配代价计算:根据第一步得到深度假设后, 计算邻域帧的特征映射到参考帧对应的深度层下的特征相似性, 然后根据计算得到的特征相似性采用1×1×1卷积和sigmoid函数计算每个像素邻域帧的权重, 根据该权重值和特征相似性计算最终的匹配代价; ④自适应匹配代价聚合:自适应采样一些邻域内像素对应的深度假设, 计算邻域像素相对于中心像素的深度图相似性, 根据特征相似性和深度图相似性计算代价聚合的权重值, 最后采用1×1×1卷积进行匹配代价聚合;⑤深度图回归:采用softmax函数将匹配代价聚合值回归得到各个像素对应的深度值;⑥深度图优化:将估计的深度图分辨率从W/2×H/2提高到W×H, 并基于MSG-Net[13], 设计一个深度残差网络, 使用RGB图像优化估计的深度图。
考虑PatchmatchNet方法在深度图随机初始化带来的较大计算量以及该方法模型需要依赖深度图真值监督的局限性, 本文对此做出一些改进。
2 多视图传播无监督网络设计
本文提出的多视图传播无监督三维重建方法继承了PatchmatchNet方法利用从粗到细的框架估计深度图的思想, 整体网络结构框架分为多尺度特征提取、深度图初始化、自适应传播、自适应匹配代价计算、自适应匹配代价聚合、深度图回归和多指标损失函数, 相比于PatchmatchNet方法主要做两点改进。
从第1节可知PatchmatchNet方法[10]在深度图初始化阶段采用的是随机初始化方法, 该方法需要比较大的计算量; 考虑到采用Colmap[6]、SLAM[14]等方法获取图像的相机参数(内参和外参), 在这过程中也获得了三维模型的稀疏点。基于这些稀疏点, 本文提出通过三角剖分[15]获得深度图的方法取代PatchmatchNet网络中深度图随机初始化方法, 简化了网络结构,加快了网络的运行时间。
另外, PatchmatchNet方法[10]属于有监督的三维重建方法, 在网络训练过程中, 需要采用深度图真值进行监督训练, 这些深度图真值的质量取决于激光雷达、深度相机等设备的质量, 且存在设备受限获取不了深度图的问题。因此, 本文提出多指标的损失函数, 从大规模的无监督数据中挖掘自身的监督信息, 使得该网络不需要依赖3D地面真实数据监督就能获得较好的精度, 且网络的普适性得到大幅度提升。
综上所述, 整体网络结构如图 1所示, 由多尺度特征提取器、基于学习的Patchmatch网络(网络结构详见图 2)和空间细化模块组成。
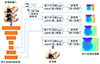 |
图1 整体网络结构 |
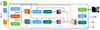 |
图2 基于学习的Patchmatch网络结构 |
2.1 多尺度特征提取
在N张尺寸为W×H图片中, 定义I0为参考图像, {Ii}i=1N-1表示邻域图像。采用FPN[16]特征提取网络从输入的图像中, 以多个分辨率分层提取特征, 用于基于学习的Patchmatch网络框架中, 以从粗到细的方式不断推进深度图估计。
2.2 基于学习的Patchmatch网络
基于学习的Patchmatch网络主要分为:初始化深度图、深度假设自适应传播、自适应匹配代价计算、聚合和深度图计算。相比于传统的Patchmatch使用倾斜平面的方法(每像素对应的深度假设包括深度值和对应的法向量), 为了减小计算量, 采用MVSNet方法[1]中使用的前向平行平面(假设像素在相机坐标系下平行于图像平面, 对应的深度假设只包含深度值), 具体结构如图 2所示。
2.2.1 深度图初始化
PatchmatchNet方法[10]的第一次迭代中, 预定义一个深度范围[dmin, dmax], 并在逆深度范围中随机初始化深度图。本文提出的方法在这方面进行了改进, 考虑实际过程中, 通过Colmap[6]、SLAM[14]等方法获取图像的相机参数(内参和外参)的同时, 也可以获得模型的稀疏点, 因此本文通过这些稀疏点初始化深度图, 具体方法是: ①根据深度范围定义深度图的4个角点, 界定感兴趣区域; ②基于定义的深度图区域, 将稀疏点通过几何变换投影到对应帧上, 获得稀疏深度图; ③采用三角剖分[15]算法对投影后的的稀疏点进行处理, 即根据3个稀疏点构成的三角形平面, 在该平面内插值获得其他点的深度信息进而获得完整的深度图, 具体流程如图 3所示。
三角剖分算法主要分为4步:
1) 根据(1)式的转换关系, 将稀疏点的像素Pu的齐次坐标转换到相机坐标下, 求得三角形3个顶点的相机坐标[X Y Z]′。
式中: K为相机内参;fx, fy为焦距; cx, cy为相机光轴在图像坐标系的偏移量; 像素Pu的齐次坐标[u v 1]′; Z为深度值。
2) 通过三角形3个顶点的相机坐标求得三角形组成的平面的法向量n, 如(2)式所示。
式中: p0, p1, p2是平面内3个点的坐标。
3) 根据三角形平面的法向量n和一个顶点的坐标p0求得该三角形平面方程L, 如(3)式所示。
式中: n=(n1, n2, n3); 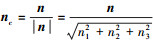 。
。
4) 将每个三角形进行栅格化得到面内投影的每一个像素坐标Pu, 再根据三角形平面方程L和像素坐标与相机坐标的转换关系K-1在每个三角形平面内插值得到对应的深度值, 如(4)式所示。
本文提出通过稀疏点进行三角剖分[15]获得深度图的方法取代PatchmatchNet[10]网络中深度图随机初始化方法, 从而缩短网络的运行时间。
 |
图3 深度图初始化流程图 |
2.2.2 自适应传播
大部分传统的方法从静态的邻域中传播深度假设, 但是深度图的空间一致性往往只对一个表面上的像素成立, 所以希望在采样邻域的过程中只采样和当前像素在同一表面上的邻域。即采用2D卷积学习每个像素p的Kp个邻域的额外偏移量{Δoi(p)}i=1Kp, 并通过双线性插值获得深度假设, 实现自适应传播, 如(5)式所示, 加快算法的收敛速度, 提升精度。
式中: {oi}i=1Kp为固定的偏移量;Dp(p)为每个像素p深度假设集合;D为上个阶段输出的深度图。
2.2.3 自适应匹配代价计算
自适应匹配代价计算即计算图像特征相似度, 通过自适应传播获得所有深度假设后, 在参考帧的深度假设下建立前向平行平面, 采用可微单应性变换将邻域帧的图像特征映射到这些平面中, 可微单应性变换如(6)式所示。
式中: pi,j为参考帧在深度dj下的像素p映射到邻域帧i下的像素位置; {Ki}i=0K为参考帧0和邻域帧i的相机内参; {[R0,i|t0,i]}i=1K为参考帧0和邻域帧i的相机外参; dj=dj(p)为像素p对应深度假设。
根据邻域帧映射到参考帧上的图像特征和参考帧的图像特征计算相似度, 进而获得每个像素的匹配代价。具体是将图像特征通道分为G组以降低内存, 然后计算第g组的特征相似度, 如(7)式所示。
式中: 〈·, ·〉表示内积; C为特征通道数; F0(p)∈ RC为像素p的特征; Fi(pi,j)∈ RC为像素p映射到邻域帧i下对应的特征; Si(p, j)∈ RG为群相似性向量。
2.2.4 自适应空间代价聚合和深度回归
根据每组的特征相似度, 采用1×1×1卷积和sigmoid函数计算每个像素的邻域帧的权重ωi(p), 然后根据这些像素级视图权重为像素p和第j个深度假设计算每组特征相似性S(p, j), 如(8)式所示。
式中,N-1为邻域帧数量。
考虑多尺度特征提取器在空间域中聚合了来自大感受野的相邻信息, 为防止跨表面边界聚合问题, 采用2D卷积学习每个像素p的额外2D偏移量{Δpk}k=1Ke, 并使用特征权重ωk和深度权重dk分配第k个邻域的贡献权重, 然后采用1×1×1卷积聚合G组匹配代价 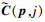 , 定义为
, 定义为
式中: C为邻域像素的匹配代价, 通过采样位置(p+pk+Δpk,j)k=1Ke处的特征相似度双线性插值到邻域位置获得; Ke为邻域像素的个数。
在深度图回归中, 使用softmax函数将代价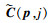 转化成置信度P, 然后根据每层深度假设值与对应的置信度值求期望获得像素p处的深度值D(p), 如(10)式所示。
转化成置信度P, 然后根据每层深度假设值与对应的置信度值求期望获得像素p处的深度值D(p), 如(10)式所示。
式中,m为深度层数。
2.3 深度图优化
深度图优化首先将估计的深度图的分辨率从W/2×H/2提高到W×H, 然后使用RGB图像优化估计的深度图。基于MSG-Net[13], 设计一个深度残差网络, 网络输出一个残差值加到Patchmatch的上采样估计中, 以获得细化的深度图。为了避免对某个深度比例产生偏差, 先将深度图归一化到[0, 1], 并在细化后将深度图反归一化回原始深度范围。
2.4 多指标损失函数
PatchmatchNet[10]方法采用数据集的深度图真值监督网络预测的深度值, 本文在这方面做出改进, 提出多指标损失函数, 实现无需借助深度真值进行训练也能重建得到较好的精度。多指标损失函数包括光度一致性损失、结构相似性损失和深度平滑损失。
光度一致性损失的关键思想是在同一视图上计算邻域帧与参考帧的颜色差异, 即根据(6)式将N-1个邻域帧Ii映射到参考帧I1上以计算颜色差异, 另考虑到一些像素可能被映射到图像的外部区域, 定义映射过程中的二进制有效掩码为Mi, 光度一致性损失计算如(11)式所示。
式中: I′i为邻域帧Ii映射到参考帧I1的图像; ∇表示梯度算子; ⊙表示点积; ‖‖1表示1-范数; ‖‖2表示2-范数。
结构相似性损失的关键思想是在同一视图上计算邻域帧与参考帧之间的相似性, 同理, 根据(6)式将邻域帧映射到与参考帧同一视图上, 根据(12)式计算2个图像之间的相似度。
式中: μx为参考帧的均值; μy为邻域帧的均值; σx为参考帧的标准差; σy为邻域帧的标准差; σxy为参考帧与邻域帧之间的协方差; c1, c2为常数, 是避免分母为0的平滑因子。
定义结构相似性损失为
深度平滑损失的关键思想是深度图变化较大的区域对应的RGB值变化也相对较大,定义深度平滑损失为
式中: ∂xDij表示深度图x方向的梯度; ∂xXij表示RGB图x方向的梯度; ∂yDij表示深度图y方向的梯度; ∂yXij表示RGB图y方向的梯度。
综上所述, 定义无监督三维重建网络的损失为
式中, λ1, λ2, λ3为权重参数。
3 实验与分析
本文所提出的Uns-PMVSNet方法在DTU数据集[17]、Tanks & Temples数据集[18]和自制数据集下进行评估, 验证本方法的性能和泛化性。
3.1 实验数据
DTU数据集[17]是具有128个不同场景的室内多视图立体数据集, 利用一个搭载可调节亮度灯的工业机械臂对每个物体拍摄49个视角, 每个视角共有7个不同亮度, 且所有场景有相同的相机轨迹; Tanks & Temples数据集[18]是室外大型场景高分辨率图像, 由现实环境中的视频序列提供, 其中测试数据分为中级组和高级组。由于上述2个数据集都是通过专业的设备, 且是固定距离拍摄的, 因此为更好地验证本文方法的泛化能力, 确保结果的可靠性, 采用自制数据集进行验证。自制数据集是西北工业大学的标志性雕像, 数据集包含300张水平360°视角的图片, 采用1 200万像素的手机在阳光下任意距离拍摄获得, 且未对图像做滤波、曝光补偿等任何处理。
3.2 实验细节
本文使用了Pytorch框架实现该模型, 并在DTU数据集[17]下进行训练和测试, 选择场景: 1, 4, 9, 10, 11, 12, 13, 15, 23, 24, 29, 32, 33, 34, 48, 49, 62, 75, 77, 110, 114, 118作为测试集, 其他作为训练集, DTU训练集是分辨率为640×512的图像, 测试集是1 600×1 200的图像; 输入图像数量设置为5, 将阶段3, 2, 1的Patchmatch迭代次数分别设置为2, 2, 1, 传播的邻域个数设置为16, 8, 0, 学习率设置为0.001;结构相似性损失中图像均值、标准差和协方差采用平均池化实现, 平滑因子c1为0.000 1, c2为0.000 9;多指标损失函数权重参数(λ1, λ2, λ3)分别设置为12, 6, 0.05;网络在NVIDIA RTX A6000服务器上进行训练, 在NVIDIA GTX 1650 GPU上进行测试。
为进一步验证本文方法的泛化能力, 在更复杂的室外数据集Tanks & Temples[18]和自己制作的数据集下测试了本文方法。另外, 2.2.1节提出采用稀疏点进行深度图初始化的方法中, 这些稀疏点以及相机内参、外参和深度范围是由Colmap[6]方法计算得到。
3.3 实验结果
为了验证本文提出的Uns-PMVSNet方法的性能, 在DTU数据集[17]上进行测试并与其他MVS方法进行重建效果对比, 如图 4所示。从图 4可以看出, 本文提出的Uns-PMVSNet方法重建效果比3D激光扫描得到的地面真实点更好, 比有监督的PatchmatchNet方法重建效果略差一点, 相比于无监督的JDACS[19]方法重建效果更好。
本文方法在DTU测试集[17]上的部分重建结果如图 5所示, 另外, 为验证本方法的泛化能力, 在Tanks & Temples数据集[18]和自己制作的数据集上进行实验, 在Tanks & Temples数据集上的部分重建重建结果分别如图 6所示, 在自制数据集上重建结果如图 7所示。在图 6中, 可以观察到重建结果呈现出较好的细节保留和几何形状的精确重建, 图中的物体轮廓清晰可见, 纹理细节也得到了良好的恢复。图 7表明, 本文方法在自制数据集下仍能展现出令人满意的重建效果, 具备较强的泛化性能。
 |
图4 DTU数据集部分场景重建结构对比图 |
 |
图5 DTU数据集上的部分重建结果 |
 |
图6 Tanks & Temples数据集上的部分重建结果 |
 |
图7 自制数据集上的重建结果 |
3.4 实验评估
将本文方法在整体质量、显存消耗和运行时间上与几种先进的重建方法进行对比, 证明本文方法的先进性能。
3.4.1 质量评估
使用距离度量[17](越低越好)评估本文提出的Uns-PMVSNet在DTU数据集[17]上的重建质量, 规定输入图像的分辨率为1 600×1 200, 评估结果如表 1所示。
距离度量包括精度度量、完整度度量和整体质量度量。精度度量是测量重建点与地面真值的平均距离, 衡量重建点的质量; 完整度度量是测量地面真实点到重建的平均距离, 衡量重建模型表面的完整性; 整体质量度量是综合精度和完整度, 计算精度和完整度的平均值。从表 1可以看出, 本文提出的Uns-PMVSNet方法重建的整体质量仅略低于部分有监督方法,在传统几何方法和无监督方法中具有较强的竞争力。
DTU数据集上的评估结果
3.4.2 显存和时间消耗对比
本文提出的Uns-PMVSNet方法在运行所耗显存和时间上较以往的大部分方法有很大的竞争力, 规定输入图像的分辨率为1 600×1 200, 运行网络所耗GPU内存为2.6 GB, 运行时间为1.0 s左右,如图 8所示。在图像分辨率同为1 600×1 200情况下, 在有监督的方法中, 如MVSNet[1]、CVP-MSVNet[4]、PatchmatchNet[10]等, 本文提出的方法在消耗显存方面比MVSNet[1]少88.6%左右, 比CVP-MVSNet[4]少75%左右, 比PatchMatchNet[10]少0.1 GB显存; 在运行时间方面比MVSNet[1]少63%左右, 比CVP-MVSNet[4]少41.2%左右; 重建DTU数据集中每一个场景三维模型时, PatchmatchNet[10]耗时为80 s左右, 而本文方法只需要74 s左右, 比PatchmatchNet[10]具有更快的运行速度。在同为无监督的方法中, 如MVS[24]、M3VSNet[12]、JDACS[19]等, 本文提出方法在显存消耗方面比MVS[24]和M3VSNet[12]少88.9%左右, 比JDACS[19]少75%左右; 在运行时间方面比MVS[24]和M3VSNet[12]少64.3%左右, 比JDACS[19]少44.4%左右。综上所述, 本文提出的Uns-PMVSNet实现了优越的性能, 在显存和运行时间消耗上具备较强的竞争力。
 |
图8 不同网络的GPU内存和时间消耗对比图 |
4 结论
本文提出了Uns-PMVSNet, 这是一种基于多视图传播的无监督三维重建方法, 该网络改进了PatchMatchNet深度图初始化这部分结构, 采用三角剖分方法进行深度图初始化, 降低了网络的复杂度, 提高了网络运行时间。同时, 基于该改进网络, 提出无监督的三维重建方法。在DTU、Tanks & Temples和自己制作的数据集上的实验表明, 本文提出的方法相较于采用3D成本体积正则化的方法, 在运行速度上少快1.7倍, 在内存使用量方面少75%;相较于当前已知的无监督的MVS方法, 本文方法在GPU内存消耗和耗时方面展现出显著的优势; 此外, 在重建精度、完整度和整体质量方面超过了许多已有的无监督MVS方法, 具备较强的竞争力。
References
- YAO Y, LUO Z X, LI S W, et al. MVSNet: depth inference for unstructured multi-view stereo[C]//15th European Conference on Computer Vision, 2018: 785–801 [Google Scholar]
- GALLUP D, FRAHM J M, MORDOHAI P, et al. Real-time plane-sweeping stereo with multiple sweeping directions[C]//2007 IEEE Conference on Computer Vision and Pattern Recognition, 2007: 1–8 [Google Scholar]
- YAO Y, LUO Z X, LI S W, et al. Recurrent MVSNet for high-resolution multi-view stereo depth inference[C]//32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019: 5520–5529 [Google Scholar]
- YANG J, MAO W, ALVAREZ J, et al. Cost volume pyramid based depth inference for multi-view stereo[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2022, 44(9): 4748–4760 [Google Scholar]
- GALLIANI S, LASINGER K, SCHINDLER K. Massively parallel multiview stereopsis by surface normal diffusion[C]//2015 IEEE International Conference on Computer Vision, 2015: 873–881 [Google Scholar]
- SCHÖNBERGER J L, FRAHM J M. Structure-from-motion revisited[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016: 4104–4113 [Google Scholar]
- XU Q, TAO W. Multi-scale geometric consistency guided multi-view stereo[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019: 5478–5487 [Google Scholar]
- BARNES C, SHECHTMAN E, FINKELSTEIN A, et al. PatchMatch: a randomized correspondence algorithm for structural image editing[J]. ACM Transactions on Graphics, 2009, 28(3): 24 [Google Scholar]
- BLEYER M, RHEMANN C, ROTHER C. PatchMatch stereo-stereo matching with slanted support windows[C]//British Machine Vision Conference, 2011 [Google Scholar]
- WANG F, GALLIANI S, VOGEL C, et al. PatchmatchNet: learned multi-view patchmatch stereo[C]//IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021: 14189–14198 [Google Scholar]
- KHOT T, AGRAWAL S, TULSIANI S, et al. Learning unsupervised multi-view stereopsis via robust photometric consistency[J/OL]. (2019-05-07)[2023-03-17]. https://arxiv.org/abs/1905.02706 [Google Scholar]
- HUANG B, YI H, HUANG C, et al. M3VSNET: unsupervised multi-metric multi-view stereo network[C]//IEEE International Conference on Image Processing, 2021: 3163–3167 [Google Scholar]
- HUI T W, LOY C C, TANG X O. Depth map super-resolution by deep multi-scale guidance[C]//14th European Conference on Computer Vision, 2016: 353–369 [Google Scholar]
- MUR-ARTAL R, TARDÓJ D. ORB-SLAM2: an open-source slam system for monocular, stereo, and RGB-D cameras[J]. IEEE Trans on Robotics, 2017, 33(5): 1255–1262. [Article] [CrossRef] [Google Scholar]
- SHEWCHUK J R. Delaunay refinement algorithms for triangular mesh generation[J]. Computational Geometry & Applications, 2014, 47(1/2/3): 741–778 [CrossRef] [Google Scholar]
- LIN T Y, DOLLÁR P, GIRSHICK R, et al. Feature pyramid networks for object detection[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition, 2017: 936–944 [Google Scholar]
- AANAES H, JENSEN R R, VOGIATIZIS G, et al. Large-scale data for multiple-view stereopisis[J]. International Journal of Computer Vision, 2016, 120(2): 153–168. [Article] [CrossRef] [Google Scholar]
- KNAPITSCH A, PARK J, ZHOU Q Y, et al. Tanks and temples: benchmarking large-scale scene reconstruction[J]. ACM Transactions on Graphics, 2017, 36(4): 1–13 [Google Scholar]
- XU H, ZHOU Z, QIAO Y, et al. Self-supervised multi-view stereo via effective co-segmentation and data-augmentation[C]//35th AAAI Conference on Artificial Intelligence, 2021: 3030–3038 [Google Scholar]
- FURUKAWA Y, PONCE J. Accurate, dense, and robust multiview stereopsis[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2010, 32(8): 1362–1376. [Article] [Google Scholar]
- CAMPBELL N, VOGIATZIS G, HERNÁNDEZ C, et al. Using multiple hypotheses to improvedepth-maps for multi-view stereo[C]//10th European Conference on Computer Vision, 2008: 766–779 [Google Scholar]
- JI M, GALL J, ZHENG H, et al. SurfaceNet: an end-to-end 3D neural network for multiview stereopsis[C]//2017 IEEE International Conference on Computer Vision, 2017: 2326–2334 [Google Scholar]
- YU Z, GAO S. Fast-MVSNet: sparse-to-dense multi-view stereo with learned propagation and gauss-newton refinement[C]//IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020: 1946–1955 [Google Scholar]
- DAI Y, ZHU Z, RAO Z, et al. MVS2: deep unsupervised multi-view stereo with multi-view symmetry[C]//2019 International Conference on 3D Vision, 2019: 1–8 [Google Scholar]
All Tables
All Figures
 |
图1 整体网络结构 |
| In the text | |
 |
图2 基于学习的Patchmatch网络结构 |
| In the text | |
 |
图3 深度图初始化流程图 |
| In the text | |
 |
图4 DTU数据集部分场景重建结构对比图 |
| In the text | |
 |
图5 DTU数据集上的部分重建结果 |
| In the text | |
 |
图6 Tanks & Temples数据集上的部分重建结果 |
| In the text | |
 |
图7 自制数据集上的重建结果 |
| In the text | |
 |
图8 不同网络的GPU内存和时间消耗对比图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


