| Issue |
JNWPU
Volume 38, Number 2, April 2020
|
|
|---|---|---|
| Page(s) | 333 - 340 | |
| DOI | https://doi.org/10.1051/jnwpu/20203820333 | |
| Published online | 17 July 2020 | |
Data Collection Method of Large Scale WSNS Mobile Node Based on Compressed Sensing and Intelligent Optimization
采用压缩感知与智能优化的大规模WSNs移动稀疏数据收集
1
School of Computer Science, Xi'an Aeronautical University, Xi'an 710077, China
2
School of information and Engineering Sciences, Norwegian University of Science and Technology, Alesund
3
School of Computer Science, Northwestern Polytechnical University, Xi'an 710072, China
Received:
13
January
2019
Aiming at the defects of large-scale large scale wireless sensor network data processing network traffic and high task latency, a data collection scheme of mobile node based on discrete elastic collision optimization algorithm and adaptive block compression sensing is proposed. Firstly, by analyzing the relationship between the network partitioning and the node deployment, an adaptive block compressed sensing data collection strategy is proposed to realize sensor node based on adaptive network block compressed sensing data collection. Designing mobile node data acquisition path planning strategy and multiple mobile nodes The collaborative computer system adopts the fitness value constraint transformation processing technology and the parallel discrete elastic collision optimization algorithm to achieve the purpose of balancing network node energy consumption and reducing data processing task delay. Finally, the simulation results show that the data collection scheme can effectively realize high-efficiency processing of large-scale sensor network data, and reduce network traffic and network task delay, and better balance network node energy consumption.
摘要
针对大规模无线传感网数据处理网络流量大、任务时延高的缺陷,提出了一种基于自适应块压缩感知与离散弹性碰撞优化算法的移动节点数据收集方案。首先,通过分析网络分块与节点部署之间的关系,提出自适应块压缩感知数据采集策略,实现传感器节点基于自适应网络块压缩感知数据采集;设计移动节点数据采集路径规划策略和多移动节点协同计算机制,通过采用适应度值约束变换处理技术和并行离散弹性碰撞优化算法,达到均衡网络节点能耗和降低数据处理任务时延的目的。最后,仿真结果表明,该数据收集方案能够有效实现大规模传感网数据高效处理,而且降低了网络流量和网络任务时延,更好均衡了网络节点能耗。
Key words: wireless sensor networks / compressive sensing / discrete elastic collision optimization / data collection
关键字 : 无线传感器网络 / 压缩感知 / 离散弹性碰撞优化 / 数据收集
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
无线传感器网络(wireless sensor networks, WSNs)为人类灵活快速地获取各种资源信息, 实时有效的监控目标区域状态提供了可能[1], 并被广泛应用于环境检测、森林火灾预警、军事国防等领域。然而计算存储能力有限、服务模式单一、资源浪费严重等已成为制约WSNs深度发展的瓶颈问题[2]。然而, 随着WSNs规模的不断扩大, 需要处理的节点数据呈现爆炸式增长, 这对WSNs通信能力、能耗来说将是极大的挑战。由于大规模WSNs中的监测事件远远小于传感器节点数量, 因此在均衡网络能耗的同时保证可靠稀疏数据采集是大规模WSNs最关键的问题。压缩感知(compressive sensing, CS)理论[3]、移动Agent(mobile agent, MA)[4]等技术的不断成熟,有效提高了大规模WSNs数据采集效率, 如何设计更加稳定高效的CS以及MA策略仍是当前WSNs数据采集研究热点。为此学者开展了相关系列研究:李鹏等[5]提出了一种基于压缩感知和树分解路由优化的数据收集方法, 分为稀疏处理和路径优化2个步骤, 保证了数据收集的高精度, 但是随着网络规模的增大, 路径优化计算呈现爆炸式增长; 文献[6]提出了基于区域化压缩感知的数据收集方法, 将每个区域独立执行压缩感知, 从而避免在数据传输过程形成较大的数据流, 但是测量矩阵设计较为复杂; 文献[7]提出了一种将压缩感知和Pegasis路由协议相结合的数据收集方案, 通过在通信链路中压缩数据实现延长网络生存周期的目的, 但没考虑链路不可靠情况且网络能耗并不一定能够达到最小期望值; WU等[8]提出了一种将LEACH分簇和压缩感知结合的数据收集算法, 实现了较高效率的网络数据收集, 但该算法没有充分考虑簇内节点数据相关性, 链路鲁棒性较差容易导致节点能耗过快。
但上述研究均未考虑移动节点对稀疏数据采样过程的影响, 同时, 稀疏信号重构算法的性能也直接影响着最后数据收集结果的可信度[9], 目前大规模数据处理效率低、重构算法参数难以选择、信号稀疏度事先确定等缺陷仍是亟需解决的问题:①改进算法往往简单融合不同类型进化策略, 并没有深入分析融合的合理性; ②大多数优化算法虽然扩展了种群搜索空间, 但是缺少种群样本多样性理论分析支撑;③改进优化算法很大程度上增加了实现难度和计算复杂度, 然而这些牺牲代价却没有得到足够重视。本文模拟物体间极短的相互作用过程, 以碰撞前后物理量变化作为学习进化机制, 提出一种智能优化算法——弹性碰撞优化算法(elastic collision optimization algorithm, ECO)并加以离散化, 同时从理论角度对算法收敛性和全局寻优能力进行分析。
针对上述问题, 本文以大规模传感网稀疏数据收集为应用背景, 提出一种自适应块压缩感知与离散弹性碰撞优化算法的数据采集方案:对涉及的自适应块压缩感知数据采集策略、移动节点数据采集路径规划以及多移动节点协同计算机制进行详细描述, 以达到减少网络数据通信总量、降低网络时延和能耗要求的目的。
1 网络模型
压缩感知理论的提出为信号采集处理带来了全新研究思路, 其利用低维空间少量观测数据就能够实现对高维信号的准确感知。对于N维信号xN×1, 可以用正交矩阵ΨN×N={ψ1, …, ψN}进行表示, 即
式中, sN×1为N×1维向量。当sN×1仅有K(K≪N)个非零系数时, 则sN×1在ΨN×N是稀疏的, 稀疏度为K。通过非相关测量矩阵ΦM×N将xN×1投影到低维测量向量yM×1上, 得到M个测量数据, 即
式中, AM×N=ΦM×NΨN×N。当M≪N时, (2)式为欠定方程组, 但如果sN×1足够稀疏, 且AM×N满足RIP条件[10]时, 可以通过求解最小l0范数稀疏重构出sN×1, 即
对于某块传感网区域内大规模部署Q个传感器节点的无线传感器网络W={Si}(i=1, 2, …, Q), 利用虚拟技术将W划分为V个虚拟簇V={Zj}(Zj为第j个虚拟簇, j=1, 2, …, V), 以实现对不同区域的监控。对于虚拟簇Zj, 根据传感器节点能耗, 在满足网络覆盖要求的情况下, 选择一定节点处于工作状态(取工作节点数为G)。Zj监控区域内有N个事件源(取K为发生事件的事件源个数), 设fi表示Zj内工作节点Sij采集到的数据(i=1, 2, …, G), 则传感器数据向量XG×1=(f1, f2, …, fG)T; 设sk为第k(k=1, 2, …, N)个事件源信号强度, 则事件源信号向量sN×1=[s1, s2, …, sN]T, 有
式中, ΨG×N为传播矩阵。根据压缩感知理论, 选取M(M < G)个传感器数据就可以得到sN×1, 因此利用观测矩阵ΦM×G对XG×1进行选取, 得到测量向量yM×1
通常来说, 同一时刻N个事件源只产生少量事件(K≪N), 即sN×1是K度稀疏的。相关研究表明, 当采用(4)~(5)式列举的ΨG×N和ΦM×N时, ΦM×GΨG×N能以极大概率满足RIP条件, 因此可以利用CS技术, 只需要少量传感器节点数据, 就可以实现监控目的, 如图1所示。
采用压缩感知技术很大程度的降低了数据采集量, 但是, 在数据通信阶段对节点进行数据采集仍需消耗一定时间, 从而造成数据时延。另外, 在传感网部署初期, 节点往往是很稠密的, 此时将Zj动态的划分为C个具有相同半径RC的块, 根据网络覆盖要求可以推导出 (R为节点通信半径, η为块内最大通信跳数)。当Zj网络工作节点密度为λ时有
(R为节点通信半径, η为块内最大通信跳数)。当Zj网络工作节点密度为λ时有
显然, 每个块具有O=G/C个工作节点, 此时每个块可以等效为一个WSNs。对于Zj内第i个块(1≤i≤C), 选取位于块中心位置的节点为块中心Ci, 用来汇聚块内被采集的节点数据, 其利用ΦI×Oi选取块内I个节点进行数据采集(∑I=M), 得到观测信号yI×1i=ΦI×OiXO×1i。当所有块完成数据采集后, 移动节点按照规划路径汇集所有块中心数据, 得到测量向量yM×1={yI×1i}(i=1, 2, …, C)
从(7)式可以看出Φ′M×G为块矩阵, 令Α=Φ′M×GΨG×N, 则A也为块矩阵。由于A中含有大量“0”元素, 因此大大降低了节点数据采集量, 而且研究表明, 对于同一种稀疏信号重构算法, 当采用块观测矩阵时, 稀疏信号恢复速度更快、精度更高。
由于分块个数C越大, 块内通信次数增加; 同样C越小, 块间通信次数增加, 因此需要合理确定C大小以平衡块内和块间通信。
结论1 当网络分块C取下值时, 可以使得块内与块间通信效益最大。
式中, μ1∈(0, 1)、μ2∈(0, 1)分别为块间通信与块内通信的控制系数, 且μ1+μ2=1。
证明 确定网络分块C的目的是平衡块内和块间通信能耗, 即有minF=μ1C+μ2Γ=μ1· 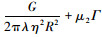 (Γ为块内通信总跳数)。如图1a)所示, 块内节点至少需要a跳到达CHi的节点数Ga=λπ(aR)2=πλa2R2, 同理需要至少a-1跳到达Ci的节点数Ga-1=πλ(a-1)2R2, 因此恰好需要a跳到达Ci的节点数G′a为
(Γ为块内通信总跳数)。如图1a)所示, 块内节点至少需要a跳到达CHi的节点数Ga=λπ(aR)2=πλa2R2, 同理需要至少a-1跳到达Ci的节点数Ga-1=πλ(a-1)2R2, 因此恰好需要a跳到达Ci的节点数G′a为
因此, 块内节点通信跳数Γ′为
所有分簇簇内节点通信跳数为
联立(10)式、(11)式有
对(12)式求偏导
(13) 式为一元三次方程, 根据卡尔丹公式法, 该方程有唯一实数解, 即
结合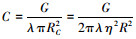 , 有
, 有
证毕。
从结论1可知, 分块个数C的大小跟网络节点密度息息相关, 这也使得块压缩感知数据采集总量因节点密度改变而改变, 其本质是动态自适应变化过程, 这样更有利于降低网络数据采集量和降低网络能耗。
K度稀疏信号sN×1满足准确重构的充分非必要条件为对于任意sN×1和常数δK∈(0, 1), 矩阵A有K阶约束等距性
对于(7)式块压缩感知模型, 观测矩阵A以极大概率满足(16)式RIP条件, 因此对于sN×1, zN×1存在(通常K≪N/2)
联立(16)式、(17)式有
因此可以得出观测次数M满足(Λ≈0.28)
对于稀疏信号sN×1精确重构问题, 目前存在的大多数重构算法需要设定K已知前提, 但是通常情况下这是不现实的, 因为无法预知有多少的事件源会发生事件, 因此为了解决稀疏度未知下信号重构问题, 以min‖s‖l0为目标优化函数, 采用智能优化算法进行求解。
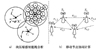 |
图1 块通信与协同计算模型 |
2 弹性碰撞优化算法(ECO)
学者们通过模拟物种生存进化规律, 提出了一系列智能优化算法, 并被广泛应用于生产生活各个领域[9]。由于智能优化算法隶属于启发式搜索算法范畴, 早熟收敛、收敛效率低仍是当前智能优化算法需要解决的关键难题。大量研究表明, 有效保持种群样本多样性是提高智能优化算法全局寻优能力的关键因素, 为此本文模拟物体对心完全弹性碰撞、完全非弹性碰撞和非完全弹性碰撞3种弹性碰撞过程, 提出一种智能优化算法:弹性碰撞优化算法[11], 关于ECO算法文献[10]已有详细介绍, 此处不再赘述。
大规模传感网稀疏数据采集主要涉及自适应块压缩感知、多移动节点协同计算和移动节点数据采集路径规划。其中, 多移动节点协同计算属于连续优化问题, 可以直接采用ECO对约束处理后的适应度值函数进行求解, 从而得到最佳多移动节点间数据协同处理方案, 而对于其他2个问题则属于离散优化问题, 本文提出离散弹性碰撞优化算法(discrete elastic collision optimization algorithm, DECO), DECO内每个粒子Xi=[xi1, xi2, …, xin]代表问题的一个解。对于稀疏信号重构问题, Xi等效为待重构信号sN×1, 每维元素取值为1或者为0, 而且取值为1的维度数恰好等于信号稀疏度K; 对于Mm移动路径规划问题, Xi维度为网络分块数C, 且每个维度取值与块中心集合{Cim}i=1:C相互对应, 即Xi-{1, 2, …, C}=Ø。无论是稀疏信号重构还是移动路径规划, 可以发现, 2个不同粒子通过一系列编码位调整可以实现相互转化, 因此结合这个特点给出DECO更新策略。
对于粒子Xi=[xi1, …, xin], 定义粒子编码对调操作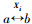 为选取Xi内第a, b维编码进行对调; 对于2个不同粒子Xi, Xj, 定义粒子转化操作Xi↔Xj为一系列编码对调操作, 即
为选取Xi内第a, b维编码进行对调; 对于2个不同粒子Xi, Xj, 定义粒子转化操作Xi↔Xj为一系列编码对调操作, 即
式中, Vi, j表示Xi↔Xj包含编码对调操作的个数。
3 移动稀疏数据收集
图1b)所示由U个可移动Sink{S1, S2, …, SU}组成, 相互之间可以直连通信。将Sink间虚拟通信网络等效为G=(V, E), 其中E={ei, j}(i, j=1, 2, …, U且i≠j)为边集, ei, j为Si和Sj之间通信时延, V={S1, S2, …, SU}为顶点集。数据采集任务执行前, 根据Sink物理位置等信息对ei, j进行更新:
1) for i=1:U
2) for j=i:U
3) refresh ei, j according to the location of Si and Sj
4) j=j+1
5) end for
6) i=i+1
7) end for
当节点间通信时延完成更新后, 节点将采集到的数据分配到其他节点, 协同完成数据处理传输任务。WSNs采集数据可能来源于任一Si, 不失一般性, 以S1数据采集为例进行分析:定义S1数据处理任务总量为H, 分配到节点Si的任务量为hi(0≤hi≤H), 节点Si任务处理速度为vi、任务处理总时间为ti, 则移动节点协同计算总时间t(H)为
从(21)式可以看出, 合理确定h=(h1, h2, …, hU)T可以使得t(H)取最小值, 此时移动节点协同计算问题转化为约束优化问题
式中, I为h搜索空间, 即
智能优化技术是求解目标优化问题行之有效的方法, 但是对于约束优化问题, 粒子目标函数值不能简单等效为粒子适应度值, 因此需要对粒子目标函数值进行约束处理。对于(23)式最小化约束优化问题, 对种群内粒子进行适应度值约束处理后, 在满足约束条件的同时能够选择适应度优秀的个体继续进化, 从而提高了算法求解约束优化问题效率和求解精度[11-12]。
4 实验仿真
利用NS3平台模拟大规模无线传感器网络, 在10 km×10 km区域内部署Q=2 000个传感器节点, 传感器节点位置信息和性能指标参数已知; 通信速率250 kb/s, 发送功率1 mW, 路由协议选取经典的LEACH协议, MAC协议采用IEEE802.15.4, 在设定时间内连续对网络进行数据采集; 利用Matlab实验仿真平台模拟多移动节点协同计算和移动节点数据采集路径规划过程, 有U=20个移动节点, 每个移动节点初始位置信息已知, 且具有相同的物理指标参数, 取移动节点数据处理速度vi=1.5 GHz, ei, j在0.08~0.12xs范围内随机生成。采用实验法给出弹性碰撞优化算法参数设置:P=300, ε=0.35, ξ=0.15, β=0.35, Tmax=500, rmin, rmax根据具体优化问题设定取值。选取文献[13]提出的DGSP数据采集算法和经典的CDG数据采集算法进行对比试验, 实验过程设定3种方案采用固定节点汇集数据的模式, 在这里使用一阶无线模型进行网络能耗分析, 即将m个比特数据传送至距离为d的节点或基站处的发送和接收能耗分别定义如下
公式中Etrans和Erecv分别表示节点发送和接收能耗。ETx-amp为信道传输能耗。Eelec为发送单个字节时的传感器节点能耗, 通常取Eelec=50 nJ/bit, ε=100 pJ/(b·m-2)。图2给出了不同重构误差要求下测量节点数M和网络能耗对比结果, 具体实验参数见表1。
从图2可以看出, 随着系统对重构误差要求的不断降低, 本文提出的自适应分块压缩感知方案和DGSP所需要的测量节点数M不断降低, 并且本文方案所需M要小于DGSP, 而CDG算法仍需要采集所有工作节点数据, 这表明, 在满足重构精度的前提下, 本文算法只需要采集少量工作节点数据, 就可以实现准确监测, 从而有效降低了网络数据通信量, 相比于其他2种方案, 数据采集量降低了约20%。对于网络能耗, 由于CDG需要多次重复采集数据以提高重构精度, 因此随着系统对重构误差要求不断降低, 网络能耗也随之下降, 但是仍远远高于本文和DGSP。对于相同系统重构误差下, 本文方案能耗要求小于DGSP, 特别的, 即使本文和DGSP在相同测量节点数M下, 本文方案能耗仍要小于DGSP, 上述实验结果表明, 自适应块压缩感知数据采集机制能够有效降低数据采集量, 而且网络节点能耗更加均衡, 网络生存周期更长。
不失一般性, 假设只有1个移动节点数据需要进行负载均衡分配, 为了分析ECO求解多移动节点协同计算问题的有效性, 分别与Greedy-LB(贪婪负载均衡算法)、WRR(加权轮转法)和文献[14]提出的CPSO-LB 3种负载均衡算法进行对比分析, 评价指标设定为数据协同计算时延, 其具体含义为数据进行负载均衡分配时间, 图3给出了3种负载均衡算法时延对比结果, 图4给出了ECO算法与遗传算法(GA)[9]、量子粒子群优化算法(QPSO)[15]目标函数收敛曲线对比结果, 图5给出了移动节点数U对数据协同计算时延的影响。
从图3可以看出, 随着任务处理量不断增加, 4重算法数据协同计算时延都在增加, 但是ECO要好于其他3种算法, 特别的当数据处理量较大(20 Gb)时, ECO数据协同计算时延优势更加明显, 约降低了50.1~77.6%。从图4可以看出, ECO算法在处理目标优化问题时, 收敛速度更快、精度更高, 只需要迭代204次就可以找到全局最优解, 要快于QPSO和GA算法。从图5可以看出, 当数据处理量较小时, 可移动节点数对数据协同计算时延影响不大, 但是当数据处理量逐渐增大时, 可移动节点数越多, 数据协同计算时延越小。上述实验表明, 对于较大数据处理任务, ECO能够给出更加优秀的负载均衡分配方案, 而且增加可移动节点数能够有效。可以看出, 移动节点以及自适应块压缩感知的引入能够大大降低网络能耗, 这是因为采用移动节点进行数据采集, 块中心节点之间无需进行数据通信, 而且路径规划以网络节点能耗均衡度为优化目标, 从而有效降低网络能耗, 延长网络生存时间。
 |
图2 不同重构误差下M和网络能耗对比 |
实验参数设置
 |
图3 3种负载均衡算法数据 |
 |
图5 移动节点数对数据协同处理时延对比计算时延的影响 |
5 结论
对大规模无线传感器网络数据采集问题进行了研究, 提出了一种基于自适应块压缩感知与离散弹性碰撞优化算法的传感网移动数据采集方案, 该方案以解决传感网大规模数据处理网络流量大、任务时延高、网络能耗不均衡等问题为目的, 设计了自适应块压缩感知、多移动节点数据采集路径规划、弹性碰撞优化算法关键技术。最后仿真实验也验证了本文传感网移动数据采集方案的有效性和突出优势。
References
- Rawat P, Singh K D, Chaouchi H, et al. Wireless Sensor Networks:a Survey on Recent Developments and Potential Synergies[J]. The Journal of Supercomputing, 2014, 68 (1): 1– 48 [Article] [CrossRef] [Google Scholar]
- Xue Y, Chang X, Zhong S, et al. An Efficient Energy Hole Alleviating Algorithm for Wireless Sensor Networks[J]. IEEE Trans on Consumer Electronics, 2014, 60 (3): 347– 355 [Article] [CrossRef] [Google Scholar]
- Ebrahimi D, Assi C. Network Coding-Aware Compressive Data Gathering for Energy-Efficient Wireless Sensor Networks[J]. ACM Trans on Sensor Networks, 2015, 11 (4): 1– 24 [Article] [CrossRef] [Google Scholar]
- Abbasi A Z, Islam N, Shaikh Z A. A Review of Wireless Sensors and Network's Applications in Agriculture[J]. Computer Standards & Interfaces, 2014, 36 (2): 263– 270 [Article] [CrossRef] [Google Scholar]
- Li Peng, Wang Jianxin, Ding Changsong. Efficient Data Collection Scheme Based on Compression Perception in WSN[J]. Journal of Automation, 2016, 42 (11): 1648– 1656 [Article] [Google Scholar]
- Yang Hao, Wang Xiwei. Data Collection Method of Wireless Sensor Network Based on Regional Compressed Sensing[J]. Journal of Computer Science, 2017, 40 (8): 1933– 1945 [Article] [Google Scholar]
- Osamy W, Salim A, Aziz A. Efficient Compressive Sensing Based Technique for Routing in Wireless Sensor Networks[J]. INFOCOMP Journal of Computer Science, 2013, 12 (1): 1– 9 [Article] [Google Scholar]
- Wu X, Xiong Y, Huang W, et al. An Efficient Compressive Data Gathering Routing Scheme for Large Scale Wireless Sensor Networks[J]. Computers & Electrical Engineering, 2013, 39 (6): 1935– 1946 [Article] [CrossRef] [Google Scholar]
- Feng Hao, Luo Lei, Wang Yong, et al. Multi Objective Data Acquisition Strategy Based on Time-Varying Multi-Agent and Genetic Algorithm in Wireless Sensor Network[J]. Journal of Communications, 2017, 38 (3): 112– 123 [Article] [Google Scholar]
- Liu Zhouzhou, Li Shining, Li Bin, et al. Resource Scheduling of Sensor Cloud Based on Elastic Collision Optimization Algorithm[J]. Journal of Zhejiang University, 2018, 52 (8): 1431– 1443 [Article] [Google Scholar]
- Liu Panpan, Li Lei, Wang Haoyu. Research on Greedy Reconstruction Algorithm Based on Variable Scale Method in Compressed Sensing[J]. Journal of Communications, 2014, 35 (12): 98– 105, 115 [Article] [Google Scholar]
- Sun Bo, Shan Xuemei, Wu Kui, et al. Anomaly Detection Based Secure In-Network Aggregation for Wireless Sensor Networks[J]. IEEE Systems Journal, 2013, 7 (1): 13 25 [Article] [CrossRef] [Google Scholar]
- Li Peng, Wang Jianxin. Data Collection Scheme Based on Sparse Projection in Wireless Sensor Networks[J]. Journal of Central South University, 2016, 47 (10): 3445– 3453 [Article] [Google Scholar]
- He Xiuli, Ren Zhiyuan, Shi Chenhua, et al. Cloud Network and Its Distributed Computing Scheme for Medical Big Data[J]. Journal of Xi'an Jiaotong University, 2016, 50 (10): 71– 77 [Article] [Google Scholar]
- Tian Jin. Study on the Improvement of Particle Swarm Optimization Algorithm, for High Dimensional Multimodal Functions[J]. Control and Decision, 2016, 31 (11): 1967– 1972 [Article] [Google Scholar]
- Mini S, Udgata S, Sabat S. Sensor Deployment and Scheduling for Target Coverage Problem in Wireless Sensor Networks[J]. IEEE Sensors Journal, 2014, 14 (3): 636 644 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 块通信与协同计算模型 |
| In the text | |
 |
图2 不同重构误差下M和网络能耗对比 |
| In the text | |
 |
图3 3种负载均衡算法数据 |
| In the text | |
 |
图4 3种算法目标函数收敛曲线图5 |
| In the text | |
 |
图5 移动节点数对数据协同处理时延对比计算时延的影响 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


