EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 447-456 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 447 - 456
DOI https://doi.org/10.1051/jnwpu/20254330447
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

压气机是航空发动机中十分重要的部件之一，其不仅对发动机的工作能力有很大影响，还对加工发动机所需要的成本也有很大影响，因此，围绕压气机性能进步所展开的研究对航空发动机的发展是十分必要的。在真实加工过程中，由于加工水平、环境干扰和一些其他不可控因素的影响，实际加工得到的压气机叶片在型面、安装角等叶型参数上难免会与设计叶片有一定的偏差，进而对压气机的气动性能及稳定性造成影响。随着加工技术的进步，现在的加工精度已经达到了很高的水平，如果继续提高加工精度来减少加工偏差的影响，会耗费过多的成本。然而，如果能够评估出叶片加工偏差与压气机气动性能及稳定性之间的定量关系，并将这部分影响考虑到压气机叶型的设计中不仅可以减少在加工技术上花费的成本，还对提升压气机性能有着重要意义。因此，关于加工偏差对压气机叶片的不确定性影响研究在近些年获得了广泛关注，目前该类研究的重点主要是几何偏差的量化及其对气动性能的不确定性影响。

国外有关加工偏差对压气机性能的不确定性影响研究开展得较早，2003年，Garzon等[1-2]使用了主成分分析法(principle component analysis, PCA)得到了某翼型的高保真几何概率分布模型并基于叶片通道分析使用蒙特卡洛模拟(Monte Carlo simulation, MCS)估算出了该翼型气动性能的统计数据。后来Lamb[3]也使用了相似的方法得到了某压气机叶片几何偏差的概率模型并进行了公差优化以减小加工偏差带来的负面影响。早期对加工偏差不确定性影响的研究开展得十分困难，数值模拟部分的工作采用叶片通道分析，而没有全部依靠CFD(computational fluid dynamics)，这主要是因为主成分分析方法需要大量几何样本并且蒙特卡洛方法也需要大量的计算时间。2009年，Lange等[4]基于某压气机叶片的实测数据用较少的叶型参数得到了叶片的几何偏差，这种方法实现了降维，因此更便于采用CFD进行不确定性分析。近些年国内外关于加工偏差影响的研究中，对叶片参数化并用相互独立的不确定变量来表示叶片的关键参数，是构建几何偏差最常见的方法之一。Giebmanns等[5]使用伴随方法研究前缘加工偏差对轴流压气机效率的影响。Wunsch等[6]使用了非嵌入式概率配置点的方法并结合稀疏网格技术，研究了叶顶间隙、前缘角及尾缘角等对某轴流压气机压比、流量等气动参数的不确定性影响。国内对加工偏差不确定性影响的研究虽起步较晚，但在近些年取得了相当大的进展。Wang等[7]改变了某压气机转子3个关键截面的前缘半径、尾缘半径、厚度和安装角，并使用神经网络建立代理模型分析了等熵效率对压气机特性线上不同工况点的不确定性影响。Ma等[8]采用了Bezier的参数化方法建立前缘半径和前缘角偏差的不确定性模型并使用了非嵌入式多项式混沌(non-intrusive polynomial chaos, NIPC)分析了前缘加工偏差对某压气机叶栅气动损失的影响。姬田园等[9-10]同样使用了NIPC进行不确定性分析，研究了安装角、弦长、厚度、前尾缘半径偏差对某压气机稳定性的影响。此外，还有学者基于叶片几何参数偏差的影响开展了鲁棒性优化[11-12]。可以看出，改变叶型关键参数的方法可以明显减少样本数，使数值模拟工作更容易展开。

关于国内外学者使用的不确定性分析方法，主要包括了MCS[13-14]、伴随方法[15-16]、NIPC[17-18]以及代理模型[19-20]等。根据现有的不确定性分析结果进行总结可以发现，对效率影响较为明显的叶型参数包括了厚度、前缘半径和弦长等[5-6, 9]，对损失影响较为明显的叶型参数包括了前缘半径和前缘角等[8, 21]。然而，目前的研究还有需要补充的地方。首先，叶型轮廓是连续的，因此在真实加工过程中由轮廓产生的偏差会导致各叶型参数的不确定性偏差，而改变叶型关键参数的方法是将各叶型参数作为独立的变量进行变化，这可能会对不确定性影响的量化结果造成一定干扰。其次，大部分学者关注的都是压气机的效率、损失等气动性能参数及流场的变化，关于加工偏差对压气机气动稳定性影响的研究还不够充分，而稳定裕度是反映压气机在非设计工况稳定工作能力的重要气动性能参数，因此加工偏差对其影响的研究同样十分重要。

综上所述，本文以某亚声速轴流压气机转子为研究对象，为了体现加工过程中不同位置的叶型轮廓之间的相关性，建立了一种基于叶片表面的几何不确定性降阶模型来构建出由法向加工偏差所引起的叶片轮廓度偏差。随后，使用神经网络建立代理模型进行不确定性分析并根据统计学分析总结出叶片加工偏差对压气机稳定裕度的影响。最后，本文观测了由加工偏差所导致的流场细微变化，进一步了解叶片参数偏差对压气机稳定裕度的影响机理。在本文工作的基础上，今后将进一步对跨声速和超声速压气机叶片展开研究以验证本文所得结论的通用性，本文所得结论旨在为压气机叶片加工偏差对压气机稳定性影响的分析提供一定参考。

1 研究方法及对象

1.1 基元叶型建模方法

真实加工过程中，由于加工偏差的作用，实际得到的叶片型线会与最初的设计型线产生一定偏离。假设这部分偏移使叶型上某一点S d沿着叶型的法向n移动了h的距离后到达了新的位置，记为点S m, 此过程即为法向加工偏差导致的叶型轮廓度偏差, 用函数表达为

式中，C a∈ [-1, 1]表示叶表轴向位置, 当处于吸力面时C a < 0, 位于压力面时C a>0。

在实际加工过程中由不确定因素引起的加工偏差应是一个随机变量, 并且根据研究表明[22-23], 当样本数足够大的时候, 叶片加工偏差近似服从零均值的高斯分布, 此外考虑到叶片表面的连续性, 加工偏差还受到叶片轮廓的限制。因此, 用h(C a)作为零均值高斯过程的随机变量来表示加工偏差, 其定义为

式中, ∀Ca∈ K, K 是仅与C a有关的几何变量。ω∈Ω, ω为概率空间{Ω, F, P}中的随机事件。通过对h(C a, ω)进行Karhunen-Loève(K-L)展开可以将h(C a, ω)表示为

式中, ξi (ω)是均值为0方差为1且相互独立的高斯随机变量。fi (C a)和λi 分别是协方差cov(C a, 1, C a, 2)的特征函数与特征值。cov(C a, 1, C a, 2)的定义为

式中，ρ(C a, 1, C a, 2)代表了型线上2个点之间的相关性, 用公式表示为

式中, k为常数, 通过改变系数k可以控制各点之间的相关性, 本文取k=1。

根据第2类齐次FredHolm积分方程可以求得(3)式中的fi (C a)和λi 。

最后, 将(3)式代入(1)式中即可得到法向加工偏差扰动后的叶型, 但是由于λi 是不断减小的, 通常取(3)式的前有限项N KL从而实现降维, 最终得到的几何不确定性降阶模型则可以表示为

1.2 三维叶片建模方法

在基元叶型的基础上, 本研究考虑了多年来各国学者研究时采用的轮廓度和安装角公差, 最终采用航空工业标准《叶片叶型的标注、公差与叶身表面粗糙度》(HB5647-1998)中规定的1级加工精度对应的叶型轮廓度和安装角公差[24]开展轴流压气机的研究, 对应前尾缘区域轮廓度公差为0.06 mm, 叶中区域轮廓度公差为0.08 mm, 安装角公差为20′, 结合3σ准则, 取高斯随机过程的标准差为公差的1/3。

在实际叶片加工过程中, 轮廓度误差在叶片型线的不同位置上通常是不同的[25-26]。轮廓度误差概率分布的标准偏差可定义为σ, 在任意基元叶型中, 假设σ是轴向弦长的函数, 则利用其在前缘、尾缘以及压力面和吸力面的叶中位置的值对σ进行插值。该过程可以通过4阶Legendre多项式实现。

式中, αi 表示各阶φi 对应的常数系数。φi 为i阶Legendre多项式。

根据(8)式可得到某叶高型线各轴向位置标准差分布, 把叶片所有叶高截面都离散成198个节点, 节点在前缘和尾缘区域分布较密集(各39个), 叶中区域分布较稀疏。将离散节点的C a代入(8)式求得标准差, 随后联立(4)~(5)式, 最后用数值积分法求解(6)式, 获得协方差函数的特征值和特征函数。通过计算可得4个模态的贡献率几乎为零, 前3阶模态的贡献率总和大于99%, 因此, 使用前3个特征值及其对应的特征函数建立(7)式中的几何不确定性降阶模型。考虑到计算资源有限, 使用过多的随机数会导致计算量增大, 并且压气机的失速主要也与叶根及叶顶有关, 本文将基元叶型建模方法应用于转子的叶根和叶顶, 并使用1个随机数改变安装角, 因此整个过程共控制了7个输入随机数。

1.3 研究对象及数值计算方法

本文研究对象为某亚声速压气机转子。该转子是沿叶高按变功变熵设计的, 流道基本为直流道, 转速为10 765 r/min, 转子主要几何参数如表 1所示。

表1

压气机叶片几何和气动参数

本文用于数值模拟的网格是使用Numeca/Autogrid5模块生成的, 并采取了周期性和对称性假设。如图 1a)所示, 本文仅对单通道创建结构化网格, 网格拓扑使用“H-O4H-H”结构, 网格无关性验证将在后文展示。图 1b)展示了数值模拟所使用的计算域。

thumbnail 图1

转子网格和计算域示意图

数值计算使用ANSYS-CFX定常求解相对坐标系下三维雷诺时均Navier-Stokes方程, 湍流模型选择BSL(baseline k-ω model)模型, 空间离散格式为2阶迎风格式。边界条件为叶片表面和端壁面给定绝热无滑移固体壁面; 出口边界给定平均静压; 进口边界给定海平面标准状况下绝对总压(101 325 Pa), 绝对总温(288.15 K)以及径向进气方向, 全局残差下降至10-6且总性能参数无明显数值波动时认为计算收敛。计算近失速工况点时逐渐增加出口平均静压, 将能获得收敛解的最后一个工况点视为近失速工况点(near stall, NS), 要求数值计算发散时的背压条件与最后一个收敛解的背压条件相差不大于10 Pa。通过计算, 流量误差仅为0.08%。

1.4 实验校准及网格无关性验证

由于网格数量对数值模拟的潜在影响, 本文对压气机转子进行了网格无关性验证, 并将总压比、等熵效率和出口绝对气流角的计算结果与实验结果进行比较。考虑到计算资源, 本文分别以59万, 89万和119万这3个数量的网格进行计算。图 2展示了对比结果, 从图 2a)~2b)可以看出, 数值模拟结果与实验结果虽有一定偏差, 但等熵效率和总压比随无量纲质量流量(M n)的变化趋势与实验结果几乎一致, 基于相同的数值方法, 59万和89万网格数计算得出的等熵效率相差约0.3%。此外, 89万和119万网格数计算得出的总压比和等熵效率特性线几乎相同。考虑到计算资源和求解精度, 本文选择89万网格数进行数值模拟, 近壁面第1层网格的厚度设置为0.006 mm, 这确保了y +≈2。

thumbnail 图2

实验与数值计算结果对比

经过前期研究发现[27], 该压气机失速主要是由叶顶堵塞导致的, 因此在进行流场分析时将重点观察压气机叶顶通道的变化情况。

2 不确定性分析方法

2.1 不确定性输出变量定义

本文引用裕度改进量ΔS M作为不确定性分析中衡量气动性能的指标, 裕度改进量的定义为

式中：π b和m b分别是原型压气机叶片近失速点的总压比及流量; π a和m a分别是带有加工偏差叶片近失速点的总压比和流量。

为了分析加工偏差对单级轴流压气机稳定性的影响, 需要计算原型叶片和带有加工偏差叶片的近失速工况点, 这是因为ΔS M与近失速工况下的总压比和质量流量有关。样本数值模拟时计算设置与原型设置相同, 以确保结果具有可比性。

2.2 代理模型介绍及精度验证

不确定性分析需要大量的计算样本及其对应的性能参数, 直接计算成本过高。因此, 本文采用单隐藏层的BP神经网络生成样本。隐藏层神经元个数为5, 激活函数采用双极S形函数, 传递函数为purelin, 训练函数为trainlm, 学习速率设置为0.01, 训练次数大于2 000, 训练目标的最小误差设置为10-9, 输入层的节点数为7即7个不确定输入变量, 输出参数为裕度改进量。从300个样本中选取30个作为测试样本，其余作为训练样本。

本文使用决定系数(r 2)和均方根误差(e rms) 作为评价代理模型精度的指标(见(10)~(11)式)。通过计算, r 2约为0.98, e rms约为0.14%, 因此认为神经网络精度足够。图 3还给出了ΔS M预测结果和数值仿真结果的对比图, 从图 3的结果可以看出, ΔSM的计算结果与预测结果几乎呈线性关系, 这也证明预测结果较为准确。

thumbnail 图3

模型预测结果与计算结果对比

式中: xi 是真实值; x i, p是预测值; x ave是xi 的平均值; t代表样本总数。

3 结果分析

3.1 输出参数统计学分析

使用QMC方法生成3万组随机变量, 结合已建立的神经网络模型预测其对应的输出参数, 图 4展示了统计结果。

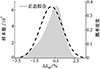thumbnail 图4

ΔS M概率密度直方图

可以看出ΔS M的分布并非服从标准正态分布, 这说明加工偏差使稳定裕度减小和增加的幅度并不相同。通过计算可以得到所有样本的ΔS M均值约为0.09%, 使稳定裕度减小的样本ΔS M均值约为-0.97%, 使稳定裕度增加的样本ΔS M均值约为0.80%。因此, 以HB5647中1级加工精度加工时, 虽然稳定裕度的平均值与设计值基本相等, 但加工偏差使压气机的稳定性具有相当大的随机性, 几何形状改变使稳定裕度降低的幅度要大于使稳定裕度增加的幅度, 最多可使稳定裕度减小约3.5%。

3.2 敏感性分析

本文使用Sobol敏感性分析来评估叶片参数对裕度改进量的影响。前文提到的研究表明, 叶片性能对厚度、前缘半径和弦长等参数比较敏感。因此, 本文进一步选取更多叶片参数, 分别为弯角(θ)、最大厚度(δ)、最大厚度位置(l)、弦长(C)、安装角(χ)、前缘半径(r LE) 和尾缘半径(r TE) 进行敏感性分析。

表 2展示了叶根和叶顶各7个叶型参数的1阶灵敏度系数(Si )和全阶灵敏度系数(Sti )。1阶灵敏度系数表示裕度改进量在某参数单独作用下对其敏感程度, 而全阶灵敏度系数表示裕度改进量在多个参数共同作用下对某个参数的敏感程度。灵敏度参数越大, 裕度改进量对该参数越敏感。

表2

叶型参数的敏感性分析结果

通过结果可以看出:

1) 综合来看, 裕度改进量对叶顶最大厚度最敏感, 其次是叶根弦长, 这说明这2个参数对稳定裕度的变化起着至关重要的作用。

2) 从全阶灵敏度系数看, 叶根最大厚度位置、叶顶弯角、叶顶弦长和叶顶安装角的1阶灵敏度系数与全阶灵敏度系数数值相差较大, 这说明这几个叶型参数可能不是因为其独立变化才对稳定裕度产生影响, 而是与叶片几何轮廓变化带来的其余叶型参数协同变化有关。从样本中分别选取上述叶型参数变化最大的前100个样本, 通过统计发现叶根最大厚度位置变化最大的100个样本中, 超过90%的样本其叶根弦长相对偏差的绝对值都大于0.2, 而叶顶弯角、叶顶弦长和叶顶安装角变化最大的样本中, 超过90%的样本其叶顶最大厚度相对偏差的绝对值都大于0.25, 这说明这些叶型参数可能是与叶根弦长或叶顶最大厚度协同变化从而对稳定裕度产生影响。

3) 其余参数, 即前缘半径、尾缘半径、叶根弯角、叶根最大厚度、叶根安装角以及叶顶最大厚度位置的1阶和全阶灵敏度系数都比较小, 这说明这些参数的偏差对裕度改进量的影响可以忽略不计。文献[5, 7]等研究表明前缘半径影响较大, 与本文结论不一致, 这可能因为本文研究了它们对压气机稳定性而非对效率等参数的影响, 并且本文研究的是亚声速压气机叶片, 前缘半径较大, 而跨声速叶片前缘半径较小, 因此本文得出前缘半径影响小也是正常的。

3.3 叶型参数偏差对流场的影响机理

结合敏感性分析结果, 在讨论加工偏差对压气机性能影响时, 应重点关注叶根弦长和叶顶最大厚度的变化。因此, 本文从前文建立的样本中选取4个转子如表 3所示，并比较了其叶型参数相对偏差及裕度改进量。可以看出, Case 1的稳定裕度有所提升而其余样本都是降低的, 其中Case 3的稳定裕度降低得最多。因此, 本文将进一步研究加工偏差是如何影响稳定裕度的。

表3

样本对比结果

选取的4个样本中, Case 3的近失速点无量纲流量最大(M n=0.71), 因此在分析4个转子时分别计算出M n为0.71时的工况点来进行比较。

前文已经说明, 压气机失速是由叶顶间隙通道堵塞造成的。因此, 加工偏差导致的压气机稳定性变化应该与叶顶泄漏流或吸力面分离流动密切相关, 因为在近失速工况下, 二者都会导致叶顶堵塞。本文选取了0, 20%, 40%, 60%, 80%及100%无量纲轴向弦长位置(Cz ), 并分别计算了6个位置在90%叶高以上的轴向流量, 表 4展示了4个转子与原型转子之间的轴向流量差值(ΔM n)在不同位置的值, 下标表示Cz 的值。轴向流量表达式为

表4

叶顶轴向流量变化对比结果

式中: ρ为流体密度; vz 为轴向速度; A为选取的叶顶区域面积; A in为进口截面面积。

可以发现, 当Cz ≥0.6时, 原型转子的叶顶轴向流量比Case 2、Case 3及Case 4高, 并且比Case 1低, 这与表 3中得到的裕度改进量的结果一致。考虑到该压气机的叶顶堵塞主要是由叶顶泄漏流和吸力面的分离流动造成的, 其中, 叶顶泄漏流在通道下游的影响相对较小, 因此叶顶泄漏流主导引发的稳定裕度变化, 通常可反映于通道上游区域的叶顶堵塞显著变化; 相比之下, 由吸力面附面层分离主导引发的稳定裕度变化, 通常反映于通道下游区域的叶顶堵塞显著变化。由于表 4的结果显示通道下游的堵塞变化与稳定裕度的变化趋势一致, 因此可以推断, 加工偏差造成的稳定性变化可能几乎不受叶顶泄漏涡的影响。此外, Case 4的轴向流量值略高于Case 2, 但其裕度改进量值较低, 这表明可能有其他因素影响Case 4的稳定裕度, 下文将对此展开分析。

图 5展示了原型转子尾缘平面上的无量纲轴向速度云图, 可以看出叶顶区域有明显的低速区, 黑色实线表示流到该低速区的流线，低速区流体主要由三部分组成, 分别标记为流动Ⅰ、Ⅱ(虚线框)和Ⅲ。流动Ⅰ和流动Ⅱ均有从叶根向叶顶流动的趋势, 流动Ⅰ源于叶根角区分离, 流动Ⅱ源于高叶展叶片上游附面层。由于叶片径向上的静压从内径到外径逐渐增大, 通道中的气流微团做曲线运动时所受的离心力和该压力差会相互平衡, 而附面层内的气流微团会随叶片一起旋转, 导致附面层内气流微团的周向分速度增大, 离心力增加, 与径向压力差无法平衡, 最终由叶根流向叶顶。因此两处流动的径向流动趋势均由附面层流动的径向压力梯度不平衡造成, 属于径向二次流。流动Ⅲ来自叶顶吸力面附面层, 下文将分别分析4个转子。

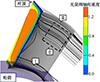thumbnail 图5

近失速工况尾缘区域无量纲轴向速度分布及流线图

首先分析叶根弦长变化明显的转子。图 6展示了它们与原型之间的静压梯度差值。云图中的变量定义为

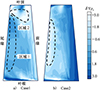thumbnail 图6

吸力面径向静压梯度差分布云图(M n=0.71)

式中：c p, a 表示有加工偏差转子的静压系数; c p, b 表示原型转子的静压系数; r表示转子径向。cp 的定义为

式中：p t, in为进口截面的总压; p in为进口截面静压。

因此, δ∇ｐr指的是叶片几何偏差导致的径向压力梯度的变化。根据图 6a), Case 1从叶根到80%叶高区域(区域1)压力梯度增加, 而从80%叶高到叶顶区域(区域2)压力梯度减小, 这表示在尾缘区域的大部分叶高范围内, 径向压力梯度相比于原型转子有所增大。因此, 图 5所示的径向二次流(即流动Ⅰ和流动Ⅱ)将有所减缓, 进而缓解叶顶的堵塞。

图 7分别给出了原型、Case 1及Case 2在99.2%叶高的无量纲轴向速度分布图, 为了进行对比将原型通道下游的低速区轮廓在Case 1和Case 2的图中用黑色虚线表示。可以看出Case 1下游的轴向速度有所增加, 所以Case 1的稳定裕度有所增加。Case 2在50%轴向弦长之前的压力梯度有所增大, 但是尾缘附近大部分区域的径向压力梯度都在减小, 因此, 如图 7c)所示, 下游的轴向速度减小, 径向二次流将会增强, 进而加剧叶顶阻塞, 最终减小Case 2的稳定裕度。

thumbnail 图7

99.2%叶高无量纲轴向速度分布云图(M n=0.71)

叶顶最大厚度存在偏差的情况与上述转子不同, 其叶顶区域的流动不仅仅受到径向压力梯度的影响, 由于吸力面型线曲率的变化, 它们还受到轴向压力梯度的影响, 因此, 几何偏差对稳定裕度的影响可能会更加复杂。图 8a)中Case 3的δ∇ｐｒ 分布与Case 1有一定相似, 但压力梯度增加的区域只出现在60%~80%叶高之间, 而80%叶高以上区域减小得十分显著。因此, 除了60%~80%叶高之间的径向二次流略有减少之外, 从叶根到叶顶区域的径向二次流(流动Ⅰ)并没有明显变化; 而80%叶高以上区域产生的二次流(流动Ⅱ)显著增强。

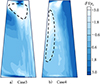thumbnail 图8

吸力面径向静压梯度差分布云图(M n=0.71)

图 9给出了原型及Case 3在99%叶高的无量纲轴向速度分布图, 并且在Case 3中将原型的低速区轮廓表示出来, 可以看出Case 3在99%叶高下的下游气流速度相比原型有所减小, 这也解释了为什么Case 3在叶顶尾缘的轴向流量最低(如表 4所示)。比较Case 4和Case 2的δΔp r分布可以发现, 靠近尾缘区域时, Case 4(见图 8b))在50%叶高以下其压力梯度减小得没有Case 2明显, 但在50%叶高以上明显减小, 因此, 来自叶根的径向二次流将在叶顶区域积累得更多。

thumbnail 图9

99%叶高无量纲轴向速度分布云图(M n=0.71)

图 10展示了叶顶轴向速度的分布, 可以看出, 与原型转子相比, Case 4的吸力面分离提前了, 这将导致压气机近失速点的低速区明显增加, 这就解释了为什么Case 4的轴向流量比Case 2高(如表 4所示), 但稳定裕度却低于Case 2, 而Case 4分离的加剧可能与其叶片变薄有关。

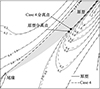thumbnail 图10

99%叶高无量纲轴向速度分布图(M n=0.71)

4 结论

本文介绍了几何不确定性降阶模型的建模方法，该方法考虑了叶型参数之间的相关性，随后以航空工业标准HB5647中1级精度的轮廓度公差为参考，用7个变量建立几何不确定性模型。在此基础上对亚声速压气机转子加工偏差的影响进行了研究，得出的主要结论如下：

1) 在本文所选的公差下，加工偏差导致的裕度改进量99.74%置信区间的上界和下界分别为3.38%和-3.19%。虽然稳定裕度的平均值几乎等于设计值，但是考虑极限情况，加工偏差最多可使稳定裕度下降3.19%。

2) 敏感性分析结果表明，对稳定裕度影响最大的叶片参数是叶顶最大厚度，其次是叶根弦长。其中，叶根最大厚度位置、叶顶弯角、叶顶弦长和叶顶安装角的1阶灵敏度系数与全阶灵敏度系数数值相差较大，这说明上述参数对压气机稳定裕度的作用有可能与压气机几何轮廓变化带来的其余叶型参数协同变化相关，而非其自身独立变化产生的影响。

3) 本文使用的压气机失速是由叶顶堵塞引起的，流场分析表明，叶根弦长偏差和叶顶最大厚度偏差都会影响吸力面的径向二次流影响进而影响叶顶通道下游的堵塞。值得注意的是，叶顶最大厚度减小还会影响吸力面上游的附面层分离，从而影响叶顶通道的堵塞。

今后的工作将利用本文的加工偏差建模及分析方法进一步研究跨声速和超声速压气机叶片以验证本文所得结论的通用性，并找到加工偏差与轴流压气机稳定性之间的通用性关系，为设计和加工压气机叶片提供一定参考。

References

  1. GARZON V E, DARMOFAL D L. Impact of geometric variability on axial compressor performance[R]. ASME GT-2003- 38130, 2003 [Google Scholar]
  2. GARZON V E. Probabilistic aerothermal design of compressor airfoils[D]. Massachusetts: Massachusetts Institute of Technology, 2003: 27–44 [Google Scholar]
  3. LAMB C T. Performance-based geometric tolerancing of compressor blades[R]. ASME GT-2004-53592, 2004 [Google Scholar]
  4. LANGE A, VOGELER K, GUMMER V, et al. Introduction of a parameter based compressor blade model for considering measured geometry uncertainties in numerical simulation[R]. ASME GT-2009-59937, 2004 [Google Scholar]
  5. GIEBMANNS A, BACKHAUS J, FREY C, et al. Compressor leading-edge sensitivities and analysis with an adjoint flow solver[R]. ASME GT-2013-94427, 2013 [Google Scholar]
  6. WUNSCH D, HIRSCH C, NIGRO R, et al. Quantification of combined operational and geometrical uncertainties in turbomachinery design[R]. ASME GT-2015-43399, 2015 [Google Scholar]
  7. WANG J, WANG B, YANG H, et al. Compressor geometric uncertainty quantification under conditions from near choke to near stall[J]. Chinese Journal of Aeronautics, 2023, 36(3): 16–29 [Google Scholar]
  8. MA C, GAO L, WANG H, et al. Influence of leading-edge with real manufacturing error on aerodynamic performance of high subsonic compressor cascades[J]. Chinese Journal of Aeronautics, 2021, 34(6): 220–232 [Google Scholar]
  9. JI Tianyuan, CHU Wuli, LI Qinghan, et al. Research blade geometric deviation affecting the compressor performance[C]//The Seventh Joint Conference on Air and Space Power and the 43rd Technical Exchange Meeting of the Third Specialized Information Network of China Aerospace, 2023 (in Chinese) [Google Scholar]
  10. JI Tianyuan, CHU Wuli, ZHANG Haoguang, et al. Uncertainty quantification of real stagger angle deviation affecting compressor performance[J]. Journal of Aerospace Power, 2024, 39: 20220858 (in Chinese) [Google Scholar]
  11. MA C, GAO L, CAI Y, et al. Robust optimization design of compressor blade considering machining error[R]. ASME GT-2017-63157, 2017 [Google Scholar]
  12. LI Zhihui. A study on robust optimization of highly loaded compressor blade-end considering fine-scale geometry deformations[D]. Beijing: Beijing Institute of Technology, 2018 (in Chinese) [Google Scholar]
  13. LANGE A, VOIGT M, VOGELER K, et al. Principal component analysis on 3D scanned compressor blades for probabilistic CFD simulation[C]//53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, 2012 [Google Scholar]
  14. SCHNELL R, LENGYEL-KAMPMANN T, NICKE E. On the impact of geometric variability on fan aerodynamic performance, unsteady blade row interaction, and its mechanical characteristics[J]. Journal of Turbomachinery, 2014, 136(9): 091005 [Google Scholar]
  15. LUO Jiaqi, ZHU Yalu, LIU Feng. Aerodynamic sensitivity analysis for manufacturing variations of a turbine blade by an adjoint method[J]. Journal of Engineering Thermophysics, 2017, 38(3): 498–503 (in Chinese) [Google Scholar]
  16. LUO J, FENG L. Statistical evaluation of performance impact of manufacturing variability by an adjoint method[J]. Aerospace Science and Technology, 2018, 77: 471–484 [Google Scholar]
  17. CAI Yutong, GAO Limin, MA Chi, et al. Uncertainty quantification on compressor blade considering manufacturing error based on NIPC method[J]. Journal of Engineering Thermophysics, 2017, 38(3): 490–497 (in Chinese) [Google Scholar]
  18. WANG Xiaojing, ZOU Zhengping. Uncertainty analysis of impact of profile geometric manufacture variations on turbine blade performance in stage environment[J]. Journal of Propulsion Technology, 2022, 43(3): 112–119 (in Chinese) [Google Scholar]
  19. JU Y, LIU Y, JIANG W, et al. Aerodynamic analysis and design optimization of a centrifugal compressor impeller considering realistic manufacturing uncertainties[J]. Aerospace Science and Technology, 2021, 115: 106787 [Google Scholar]
  20. HE X, ZHENG X. Performance improvement of transonic centrifugal compressors by optimization of complex three-dimensional features[J]. Journal of Aerospace Engineering, 2017, 231(14): 2723–2738 [Google Scholar]
  21. LIU B, LIU J, YU X, et al. A novel decomposition method for manufacture variations and the sensitivity analysis on compressor blades[J]. Aerospace, 2022, 9: 542 [Google Scholar]
  22. CHEN H, WANG Q, HU R, et al. Conditional sampling and experiment design for quantifying manufacturing error of transonic airfoil[R]. AIAA-2011-658, 2011 [Google Scholar]
  23. GAO Limin, CAI Yutong, XU Haoliang, et al. Uncertainty analysis of machining error influence of compressor blade[J]. Journal of Aerospace Power, 2017, 32(9): 2253–2259 (in Chinese) [Google Scholar]
  24. Aviation Industry Corporation of China. HB5647 Blade profile marking, tolerance and blade surface roughness [S]. HB5647-1998, 1999 [Google Scholar]
  25. DOW E A, WANG Q. Simultaneous robust design and tolerancing of compressor blades[R]. ASME GT-2014-25795, 2014 [Google Scholar]
  26. GUO Zhengtao, CHU Wuli, YAN Song, et al. Data mining on effects of manufacturing error on aerodynamic performance and stability of a compressor cascade[J]. Journal of Propulsion Technology, 2022, 43(3): 141–153 (in Chinse) [Google Scholar]
  27. LU Qing. Qualitative influence of machining deviation on critical attack angle of cascade[D]. Dalian: Dalian Maritime University, 2024 (in Chinese) [Google Scholar]

All Tables

表1

压气机叶片几何和气动参数

In the text
表2

叶型参数的敏感性分析结果

In the text
表3

样本对比结果

In the text
表4

叶顶轴向流量变化对比结果

In the text

All Figures

thumbnail 图1

转子网格和计算域示意图
In the text
thumbnail 图2

实验与数值计算结果对比
In the text
thumbnail 图3

模型预测结果与计算结果对比
In the text
thumbnail 图4

ΔS M概率密度直方图
In the text
thumbnail 图5

近失速工况尾缘区域无量纲轴向速度分布及流线图
In the text
thumbnail 图6

吸力面径向静压梯度差分布云图(M n=0.71)
In the text
thumbnail 图7

99.2%叶高无量纲轴向速度分布云图(M n=0.71)
In the text
thumbnail 图8

吸力面径向静压梯度差分布云图(M n=0.71)
In the text
thumbnail 图9

99%叶高无量纲轴向速度分布云图(M n=0.71)
In the text
thumbnail 图10

99%叶高无量纲轴向速度分布图(M n=0.71)
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.