Kinematics analysis and design of 4PC-2R parallel mechanism

Fei LUAN; Aixia LI; Xiaofeng WANG; Zizheng WANG; Xinrui MEN; Bohao ZHANG

doi:10.1051/jnwpu/20254330437

All issues

Volume 43 / No 3 (June 2025)

JNWPU, 43 3 (2025) 437-446

Full HTML

Open Access

Issue		JNWPU Volume 43, Number 3, June 2025


Page(s)		437 - 446
DOI		https://doi.org/10.1051/jnwpu/20254330437
Published online		11 August 2025

JNWPU 2025, 43(3): 437–446

Kinematics analysis and design of 4PC-2R parallel mechanism

4PC-2R并联机构设计及运动分析

Fei LUAN (栾飞)¹, Aixia LI (李爱霞)¹, Xiaofeng WANG (王晓峰)¹, Zizheng WANG (王子征)², Xinrui MEN (门鑫蕊)¹ and Bohao ZHANG (张博豪)¹

¹ School of Mechanical and Electrical Engineering, Shaanxi University of Science and Technology, Xi′an 710021, China
² Ulster College, Shaanxi University of Science and Technology, Xi′an 710021, China

Received: 18 June 2024

Abstract

With the rapid development of new energy vehicle industry, the energy supply efficiency of a heavy electric truck becomes a key factor that restricts its wide application. This paper proposes a new 3T1R parallel mechanism with movement as its motion input, which can be used in the fast power exchange of the heavy electric truck. The 2-PCR parallel mechanism is modeled with the SolidWorks software. Its degrees of freedom are examined with the helix theory and validated with the modified G-K formula. The kinematics is solved primarily with the closed-loop vector method. The Matlab is employed to graphically determine the mechanism′s working space. The results indicate the mechanism possesses 4 degrees of freedom, 3 translations across the X, Y and Z axes and 1 rotational degree of freedom around the Z axis. The movement in the Y and Z directions is independent, and the freedom of rotation around the Z axis interferes with the movement in the X direction. The output point can not only move in the X direction but also drive its rotational angle when it moves in the X direction. Based on this mechanism, the 4PC-2R parallel mechanism is proposed for further optimization. The comparison of the two mechanisms shows that the 4PC-2R parallel mechanism is smoother. Finally, the mechanism′s parameters are refined with the genetic algorithm so as to expand the working space of the 4PC-2R mechanism. The practical application of the 4PC-2R parallel mechanism demonstrates that it has a streamlined structure, an expansive operational range and fluid motion characteristics, thus being safer and more effective for a heavy electric truck′s power exchange.

摘要

针对电动重卡的换电作业过程, 设计了一种以移动副作为输入的新型3T1R并联机构。利用SolidWorks软件完成了2-PCR并联机构的三维建模。基于螺旋理论对机构的自由度进行了深入分析, 并通过G-K公式对其分析结果进行了验证, 确保了理论分析的准确性; 采用闭环矢量法对其进行运动学求解; 针对2-PCR机构X方向移动和绕Z轴转动相互干涉这一不足, 对机构进行优化得到4PC-2R并联机构。对4PC-2R并联机构进行了相应的自由度分析和运动学求解, 通过2个机构的对比, 可知4PC-2R并联机构运动更平稳。运用遗传算法优化机构参数, 进一步扩大了4PC-2R机构的工作空间, 该机构用于电动重卡的换电装置上, 可以有效提高电动重卡的换电效率和安全性。

Key words: parallel mechanism / working space / kinematics analysis / structural optimization design

关键字 : 并联机构 / 工作空间 / 运动学分析 / 结构优化设计

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

随着全球能源危机的加剧和环境污染问题的日益严重, 我国换电产业迎来了快速发展的机遇[1]。特别是在商用车领域, 电动重卡因其在降低运营成本和减少碳排放方面的潜力而备受关注[2]。但电动重卡换电模式在发展过程中仍然面临着诸多问题和挑战, 快速换电技术存在换电动作准确性不高、设备稳定性不足等问题, 降低了换电效率和可靠性[3]。

换电技术的核心在于对电池进行精准的取放操作, 这一过程不仅要求精确的定位和操作, 同时也面临着换电过程需要远距离的移动作为运动输入的挑战。此外, 由于换电电池包质量较大, 对换电装置的承载能力和稳定性提出了更高的要求。为了满足这些要求, 需要一种能够提供大载荷、高精度和大工作空间的机械装置。

能实现3T1R^Z(3个平移自由度和一个绕Z轴旋转自由度)运动的四自由度并联机构, 因其独特的性能而在众多工业机械设备中获得了广泛应用。这类并联机构的一大特点是所有驱动单元协同承担外部载荷, 确保了整个机构具备较高的承载性能, 其运动自由度也满足换电装置的动作要求, 故考虑将并联机构与换电装置结合起来。

考虑到电动重卡顶部式换电的特点, 需要以移动副作为驱动来实现换电。在众多四自由度并联机构的设计中, 以竖直方向布置的4个相互平行的移动副作为输入的并联机构有H4、I4、4-RRPaR并联机构，以及2PRPaRR-2PRPaR并联机构[4-8], 这种布置形式使机构在竖直方向有较大的移动范围, 但在其余自由度方向上的变化范围较小。以水平布置的2个平行的移动副作为驱动, 每个导轨各布置2个移动副的并联机构有4PPa-2PaR并联机构和有“二叉树”结构的并联机构[9-11]; 还有以水平布置的2个平行导轨作为移动副, 每个导轨各布置1个移动副的2PPPaR型并联机构, Angeles等提出的新移动并联机构与其末端机构相同, 但由双转动副作为驱动[12-14], 此布置形式适合水平移动范围较大的场合, 但其他方向自由度的活动范围也受限。Altuzarra等[15-18]提出了以2个呈直角形状的轨道作为运动输入的全对称并联机构, 李旭等[19]提出了与前面的机构布置形式都不同的并联机构2-PRPU, 贺阳涛等[20]提出了2个移动副作为驱动且在同一条轨道上面的2-PCR_-2-UPS非对称并联机构, 这些并联机构的设计也为后续机构的研究和开发提供了思路。

本文结合上述机构的特性以及电动重卡顶部式换电的需求, 同时也充分利用了少自由度并联机构具有的精度高、速度快、无误差积累、结构简单等优点[21-22], 设计了一种以移动副为运动输入, 可实现3T1R^Z运动的并联机构2-PCR, 并对其进行优化后得出4PC-2R机构。

1 2-PCR机构简介

对具有4个自由度的对称并联机器人机构, 该系统存在2个独立的约束条件。在动平台上施加约束的方式有2种情形: ①各分支上的连杆对动平台各自施加两重独立的约束; ②每个分支链接只对动平台施加一个约束。尽管每个分支链施加约束的数量可能不同, 但是对动平台产生实际作用的独立约束总数都被限制在最大2个线性无关的约束之内[23-26]。

1.1 机构概述

四自由度并联机器人机构设计允许其末端执行器在三维空间中进行任意平移运动, 同时还能绕垂直于基座平面的Z轴做旋转运动。约束螺旋系的标准基为

根据高等空间机构学, 本文提出以2个移动副作为运动输入, 分支自由度为4的并联机构, 机构名称与对应机构简图如表 1所示。

表1

双支链3T1R^Z四自由度并联机构列举

上述机构均以移动副作为输入, 并且能沿输入方向实现远距离移动, 适用于需要远距离位移的场景。

1.2 机构描述

2-PCR并联机构由定平台、动平台以及2个相同的支链组成, 如图 1所示。

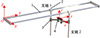图1

2-PCR并联机构模型

1.定平台(导轨) 2.滑块3.连杆4.动平台

如图 1所示, 2-PCR并联机构主要含有2条支链, 定平台的2个导轨平行布置, 滑块与定平台以移动副连接, 双支链中滑块作为导轨的部分沿竖直方向平行布置, 连杆与滑块通过圆柱副连接, 双支链的连杆通过转动副连接到动平台上。

并联机构运动链的参数描述如图 2和表 2所示。

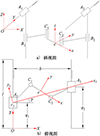图2

2-PCR并联机构简图

表2

参数定义

其中定平台以O为原点, 导轨移动的方向为Y方向, X轴垂直于Y轴, Z轴垂直于XOY基准平面, 动平台的坐标原点设定在C ₁ C ₂连线的中点。x轴正方向过C ₂点, y方向垂直于x轴, z轴按右手定则确定。

1.3 自由度分析

采用修正的反螺旋理论的G-K公式, 对所设计的并联机构进行了自由度分析, 如(2)式所示。

支链1的运动螺旋系可表示为

其对应的约束螺旋系为

支链2的约束螺旋系同上, 都限制了绕x, y轴的转动, 因此动平台受2个公共约束, 故λ=2, 由(2)式计算自由度得

机构自由度的性质可由约束螺旋系的二次反螺旋分析得出, 即

(6) 式表明该机构设计使得其末端执行器能够在三维空间中自由移动, 覆盖X, Y, Z 3个正交方向的任意位移。同时, 还赋予了绕Z轴做任意角度旋转的能力。机构运动副的相互关系不会随着机构运动而改变, 因此机构的自由度具有全周性。

2 2-PCR运动学分析

动平台z向的运动和圆柱副z向的控制有关, 故将动平台的分析转化为平面四杆机构, 由于2-PCR并联机构为对称结构, 2个连架杆的长度相等, 考虑到机构运动的特点, 两连架杆都为摆杆, 机构为反安装的等腰梯形机构, 动平台为连杆C ₁ C ₂, C ₁ C ₂的中点为E, 运动输入为(q ₁, q ₂), 运动输出为动平台E点的位置和角度(x, y, θ)。

2.1 运动学分析

以如图 3所示A ₁和A ₂处于同一水平线的位置进行分析, 以A ₁为圆心c ₁, A ₁和A ₂连线为x ₁轴, 与x ₁轴垂直的是y ₁轴。封闭矢量环如图 3所示, 根据闭环矢量方程建立各矢量的投影方程即位移方程，如(7)式所示。

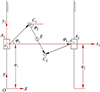图3

2-PCR机构分析位置俯视图

将位移方程对时间求导得出的速度方程写成矩阵形式，如(8)式所示。

式中

对时间t求导可得到加速度方程

式中

其中E点在坐标系x ₁ c ₁ y ₁下的位置为

根据此机构的特点, 其动坐标系到定坐标系的变换矩阵为

式中， , 故E点在定坐标系下的位置为

对时间t求导得到E点的速度方程，如(13)式所示。

式中，E点的速度大小为 , 速度方向与x轴的夹角为。

再对时间求导得到E点的加速度方程

式中，E点的加速度大小为 , 加速度方向与x轴的夹角为。

2.2 奇异位型

当det( B )=0, sinφ ₁cosφ ₁=0, 即φ ₁=0或φ ₁= 时, 机构发生第一类奇异, 又称反向运动学奇异, 在此情况下, 矩阵 B 属于病态矩阵, 且精度降低, 使机构的输入和输出运动之间的传递具有不确定性, 所以在机构运动时需避免φ ₁=0或的位置。

当det( A )=0, sinφ ₂cosφ ₃-sinφ ₃cosφ ₂=0, 即tanφ ₂=tanφ ₃时, 机构发生第二类奇异, 又称正向运动学奇异。在此情况下, 杆C ₁ C ₂, C ₂ A ₂处于同一条线, C ₂ A ₂杆有2个可能的运动方向, 机构失去了应有的稳定性和刚性, 为了防止这种情况的发生, 应限制φ ₁的运动角度使得C ₁ C ₂杆和C ₂ A ₂杆不在同一条直线上, 或控制2个作为驱动的滑块避免使C ₁ C ₂杆和C ₂ A ₂杆处于同一条直线上。

当det( A )=0和det( B )=0同时成立时, 机构处于第三种奇异, 即组合型奇异, 此时要同时考虑上面2种情况。

3 4PC-2R机构的优化分析

2-PCR机构在只沿x方向运动时, 输出杆C ₁ C ₂的角度也会随之改变, 即两者发生干涉。故提出4个自由度互不干涉的4PC-2R机构, 如图 4所示。

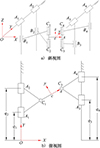图4

4PC-2R并联机构简图

此机构关键尺寸和2-PCR机构关键尺寸一致, 不同之处在于两边导轨各增加了1个滑块, 从2个滑块驱动变成了4个滑块驱动, 且动平台的输出点有更加光滑的运动曲线。

3.1 自由度分析

A_iB_iC_i 支链对应的约束螺旋系如(4)式所示, 都限制了绕x, y轴的转动, 因此动平台受2个公共约束, 故λ=2, 由(2)式计算自由度得

其约束螺旋系的二次反螺旋如(6)式所示, 表明此机构与2-PCR机构的自由度一样具有全周性。

3.2 位置正解分析

A_i , C_i 基于定平台的空间位置为

故C_i 点的坐标为

所以输出点E的坐标为

3.3 位置反解分析

已知动平台的运动输出(x, y, z, θ), 求定平台的运动输入。

C ₁, C ₃点位置可由已知的运动输出求得

由此可推导出输入值

3.4 运动算例分析

表 3和表 4展示了运动的正反解算例, 通过对比, 验证了4PC-2R机构位置分析的正确性。

表3

运动正解结果

表4

位置反解结果

3.5 速度分析

设机构驱动支链的驱动速度 ; 动平台速度 , 加速度 a = , 机构速度雅可比矩阵为 J 。

对(21)式关于时间求导, 可得

4 2个机构对比分析

4.1 工作空间

2-PCR机构和4PC-2R机构的z向是由圆柱副连接的, 整个机构的工作空间在XOY平面投影的横截面积一样。根据换电重卡电池的尺寸初步给定b=400 mm, d=230 mm, e=150 mm, l=3 000 mm。通过Matlab计算机构在XOY平面的可行域, 如图 5~6所示。

图5

2-PCR机构在XOY平面的可行域

图6

4PC-2R机构在XOY平面的可行域

图 5~6中展示的工作空间相似, 从工作空间上看, 2个机构差异较小。

4.2 E点沿X方向运动分析

E点是末端执行器的运动输出点, 输出点通常指与任务直接相关的一点或部分区域, 在实际应用中, 末端执行器的输出点需要在特定方向上具有精确的定位和控制能力。

2-PCR机构和4PC-2R机构的导轨都沿Y方向且Z向都是圆柱副, 故输出点E在这2个方向均可实现独立运动, 下面分析E点的转动能力和沿X轴方向的运动能力。

图 7为2-PCR机构E点沿X轴运动时C ₁ C ₂的角度变化图, 呈现波动趋势, 说明E点沿X方向运动且无其他方向运动时, C ₁ C ₂杆角度会随之变化, 即这2个方向的运动存在干涉。

图7

2-PCR机构C ₁ C ₂角度变化图

图 8显示4PC-2R机构可以实现沿着X方向独立运动, 即沿着Y等于某个常数的直线运动, 图 8中的弧线是输出点E沿着Y=500 mm运动时各滑块的位移, 跟机构位置反解的计算结果相符。

图8

E点沿X轴方向运动时各滑块的位移

图 9展示了输出点E在做图 8所示运动时的速度变化, 结果显示各滑块的速度是连续且光滑的, 这表示运动过程速度变化平缓, 机械系统可以平稳运行。和2-PCR机构相比4PC-2R机构在沿着X轴方向有独立且连续稳定的运动。

图9

E点沿X轴方向运动时各滑块的速度

图 7和图 8分别展示了2个机构X轴方向的运动与E点的转动之间的关系, 结果表明2-PCR机构在这2个方向上的运动相互干涉, 而4PC-2R机构在这2个方向有独立的运动, 且运动平稳。

4.3 遗传算法优化机构参数

为了提升机构的运作效能并拓展其工作范围, 本文将机构的工作空间范围作为目标函数, 以b, d, e作为优化参数, 运用遗传算法[27-28]在Matlab2021b环境下, 对其进行编程求解, 可得其收敛曲线如图 10所示。遗传算法的参数设置如表 5所示。

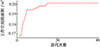图10

工作空间收敛曲线图

表5

遗传算法参数设置

经过16代的迭代之后, 目标函数趋于收敛, 进而可得优化后的机构参数, 其对应机构的工作空间面积为0.199 m², 和原有4PC-2R机构相比, 增长了0.046 m², 优化后的机构b=366.71 mm, e=132.64 mm, d=250.04 mm, 工作空间如图 11所示。

图11

优化后机构的工作空间

4.4 4PC-2R机构的工程应用分析

顶部换电式重卡需要远距离的移动作为运动输入, 这2个机构都符合此特点。在对2种机构的工作空间和输出点E沿X轴方向的运动特性进行细致分析后, 发现4PC-2R机构在提供平稳运动方面表现更为出色。这一特性对于换电装置来说至关重要, 因为在换电过程中, 任何突然或剧烈的运动都可能导致电池连接故障或设备损坏, 从而影响整个换电过程的安全性和可靠性。

此外, 4PC-2R机构的独立四自由度运动能力使其在复杂的操作环境中具有更高的适应性和灵活性。这一点在需要精确定位和调整电池位置以适配不同车型的换电装置中尤为重要。

综合考虑运动平稳性、自由度的独立性以及工作空间的优化, 得出结论: 4PC-2R机构更加符合电动重卡换电装置的实际需求。它不仅能够提供精确和平稳的运动, 还能够适应不同操作条件, 保证换电过程的高效性和安全性。

4PC-2R机构虽然在运动平稳性和适应性方面表现出色, 但在实际应用中也可能面临干涉、稳定性、机构刚度不足以及其他的潜在问题。在紧凑的空间内, 机构的运动部件可能会与其他部件或周围环境发生碰撞, 或者同一导轨的2个滑块相互干涉, 需要通过精确的几何建模和仿真分析, 以及设置相应的接近开关, 确保所有运动部件在运动过程中不会发生碰撞。同时在设计阶段考虑动态平衡, 增加支撑结构或使用高强度材料来提高机构的整体稳定性以及解决机构刚度不足的问题。可以制定定期维护计划, 使用预测性维护技术来减少意外故障, 或采用模块化设计, 便于部件的更换和升级, 减少维护难度和成本, 以应对实际应用中的潜在问题。

5 结论

本文基于螺旋理论和G-K公式, 对3T1R并联机构进行了深入研究, 提出了2-PCR机构, 并对其实现四自由度运动的能力进行了验证。然而, 2-PCR机构在性能表现方面存在不足, 为了克服这些局限性, 创新性地设计了4PC-2R机构。利用螺旋理论, 不仅证明了4PC-2R机构同样能够实现所需的四自由度运动, 还展示了其在运动性能上的显著优势。

通过对比2种机构的工作能力, 结合换电装置的工作过程, 可知4PC-2R机构具有优越的运动性能和工作空间特性, 更适合作为电动重卡换电装置的机械机构。本研究从理论上分析了4PC-2R机构的工作性能, 但并未对装置进行物理实验, 也未充分考虑机构在实际生产中的成本效益。后续将对4PC-2R机构进行样机加工、实验测试以及成本效益分析, 并为其在更广泛的工业自动化领域的应用提供更加全面的支持。

References

FANG Yongqiang. Current situation and development trend of electric heavy-duty truck power exchange mode[J]. Mechanical & Electrical Technology, 2023(5): 72–75 (in Chinese) [Google Scholar]
QI Xiaoling. Ouyang Minggao, academician of Chinese academy of sciences: analysis and prospect of new energy heavy duty truck technology pathway[N]. China Industry News, 2024-04-07(4) (in Chinese) [Google Scholar]
CHEN Hao, XIONG Meng, YANG Yang. The status quo and development trend of electric heavy truck battery swap mode[J]. Auto Time, 2024(7): 100–102 (in Chinese) [Google Scholar]
PIERROT F, COMPANY O. H4: a new family of 4-DOF parallel robots[C]//Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 1999: 508–513 [Google Scholar]
KRUT S, BENOIT M, OTA H, et al. I4: a new parallel mechanism for Scara motions[C]//Proceedings of the 2003 IEEE International Conference on Robotics and Automation, 2003: 1875–1880 [Google Scholar]
LI Z, LOU Y, LI Z. Type synthesis and kinematic analysis of a new class Schönflies motion parallel manipulator[C]//IEEE International Conference on Information and Automation, 2011: 267–272 [Google Scholar]
LI Z, LOU Y, ZHANG Y, et al. Type synthesis, kinematic analysis, and optimal design of a novel class of schönflies-motion parallel manipulators[J]. IEEE Trans on Automation Science and Engineering, 2013, 10(3): 674–686 [Google Scholar]
ZHAO Zhilong. Research on analysis optimization and trajectory planning of 3T1R parallel mechanism for coordinate assembly[D]. Harbin: Harbin Institute of Technology, 2021 (in Chinese) [Google Scholar]
YANG Guilin, WU Cuncun, CHEN Qingying, eta al. Kinematics analysis and design optimization of novel 3T1R parallel manipulator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(12): 386–394 [Article] (in Chinese) [Google Scholar]
WU C C, YANG G L, CHEN Q Y, et al. Kinematic design of a novel 4-DOF parallel manipulator[C]//IEEE International Conference on Robotics and Automation, Singapore, 2017: 6099–6104 [Google Scholar]
ZHANG F X, CHEN S L, HE Y Y, et al. A kinematic calibration method of a 3T1R 4-degree-of-freedom symmetrical parallel manipulator[J]. Symmetry, 2020, 12(3): 357 [Google Scholar]
WU Cuncun, YANG Guilin, CHEN Qingying, et al. Kinematic and performance analysis of a 4-DOF 2PPPaR parallel manipulator[J]. Journal of Mechanical Engineering, 2018, 54(3): 36–45 (in Chinese) [Google Scholar]
ANGELES J, CARO S, KHAN W, et al. Kinetostatic design of an innovative schönflies-motion generator[J]. Journal of Mechanical Engineering Science, 2006, 220(7): 935–943 [Google Scholar]
GAUTHIER J F, ANGELES J, NOKLEBY S B, et al. The kinetostatic conditioning of two-limb schönflies motion generators[J]. Journal of Mechanisms and Robotics, 2009, 1(1): 011010 [Google Scholar]
ALTUZARRA O, HERNANDEZ A, SALGADO O, et al. Multiobjective optimum design of a symmetric parallel schönflies-motion generator[J]. ASME Journal of Mechanical Design, 2009, 131(3): 031002 [Google Scholar]
ALTUZARRA O, ŞANDRU B, PINTO C, et al. A symmetric parallel schönflies-motion manipulator for pick-and-place operations[J]. Robotica, 2011, 29(6): 853–862 [Google Scholar]
HERNÁNDEZ A, ALTUZARRA O, SALGADO O, et al. Designing parallel manipulators: from specifications to a real prototype[J]. Industrial Robot, 2012, 39(5): 500–512 [Google Scholar]
LI Hongwei. Workspace and rotation capacity analysis of 4-DOF 3T1R parallel mechanism[J]. Machine Design and Research, 2020, 36(5): 75–80 (in Chinese) [Google Scholar]
LI Xu, LUO Xia, LUO Cheng, et al.. A discrete Monte Carlo approach to workspace analysis of a type of 3T1R parallel mechanism[J]. Machinery, 2020, 47(5): 27–32 (in Chinese) [Google Scholar]
HE Yangtao, MA Chunsheng, WEN Jie, et al. Kinematic analysis and workspace analysis of 2-PCR_-2-UPS parallel mechanism[J]. Science Technology and Engineering, 2023, 23(4): 1481–1487 (in Chinese) [Google Scholar]
HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Higher Space Mechanics[M]. Beijing: Higher Education Press, 2006 (in Chinese) [Google Scholar]
LI Z H, LU Q G, WANG H Z, et al. Design and analysis of a novel 3T1R four-degree-of-freedom parallel mechanism with infinite rotation capability[J]. Journal of Mechanical Engineering Science, 2022, 236(14): 7771–7784 [Google Scholar]
HUANG Zhen, ZENG Daxing. Calculation of degrees of freedom of mechanisms: principles and methods[M]. Beijing: Higher Education Press, 2016 (in Chinese) [Google Scholar]
HAN Jianyou, YANG Tong, YU Jingjun. Higher institutional studies[M]. Beijing: Machinery Industry Press, 2015 (in Chinese) [Google Scholar]
ZHU Dachang, CHEN Dehai, FENG Wenjie. Research on the integrated theory of space configuration and intelligent control of flexible and parallel mechanism[M]. Beijing: Metallurgical Industry Press, 2013 (in Chinese) [Google Scholar]
WANG Shaoxing. Design and analysis of robot structure for battery swapping of electric vehicle[D]. Harbin: Harbin Institute of Technology, 2012 (in Chinese) [Google Scholar]
LU Kai, WAN Xiaojin, LI Qinglei, et al. Workspace analysis and parameter optimization of 8-SPU parallel robot[J]. Machine Tool and Hydraulics, 2018, 46(21): 20–23 (in Chinese) [Google Scholar]
HUANG Guanyu, FANG Yuefa, QU Haibo, et al. Optimization of the motion performance of planer five-bar linkage using a genetic algorithm[J]. Journal of Beijing Jiaotong University, 2015, 39(4): 44–48 (in Chinese) [Google Scholar]

All Tables

双支链3T1R^Z四自由度并联机构列举

参数定义

运动正解结果

位置反解结果

遗传算法参数设置

All Figures

图1

2-PCR并联机构模型

1.定平台(导轨) 2.滑块3.连杆4.动平台

In the text

	图2 2-PCR并联机构简图
In the text

	图3 2-PCR机构分析位置俯视图
In the text

	图4 4PC-2R并联机构简图
In the text

	图5 2-PCR机构在XOY平面的可行域
In the text

	图6 4PC-2R机构在XOY平面的可行域
In the text

	图7 2-PCR机构C ₁ C ₂角度变化图
In the text

	图8 E点沿X轴方向运动时各滑块的位移
In the text

	图9 E点沿X轴方向运动时各滑块的速度
In the text

	图10 工作空间收敛曲线图
In the text

	图11 优化后机构的工作空间
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] FANG Yongqiang. Current situation and development trend of electric heavy-duty truck power exchange mode[J]. Mechanical & Electrical Technology, 2023(5): 72–75 (in Chinese) [Google Scholar]

[2] QI Xiaoling. Ouyang Minggao, academician of Chinese academy of sciences: analysis and prospect of new energy heavy duty truck technology pathway[N]. China Industry News, 2024-04-07(4) (in Chinese) [Google Scholar]

[3] CHEN Hao, XIONG Meng, YANG Yang. The status quo and development trend of electric heavy truck battery swap mode[J]. Auto Time, 2024(7): 100–102 (in Chinese) [Google Scholar]

[4] PIERROT F, COMPANY O. H4: a new family of 4-DOF parallel robots[C]//Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 1999: 508–513 [Google Scholar]

[5] KRUT S, BENOIT M, OTA H, et al. I4: a new parallel mechanism for Scara motions[C]//Proceedings of the 2003 IEEE International Conference on Robotics and Automation, 2003: 1875–1880 [Google Scholar]

[6] LI Z, LOU Y, LI Z. Type synthesis and kinematic analysis of a new class Schönflies motion parallel manipulator[C]//IEEE International Conference on Information and Automation, 2011: 267–272 [Google Scholar]

[7] LI Z, LOU Y, ZHANG Y, et al. Type synthesis, kinematic analysis, and optimal design of a novel class of schönflies-motion parallel manipulators[J]. IEEE Trans on Automation Science and Engineering, 2013, 10(3): 674–686 [Google Scholar]

[8] ZHAO Zhilong. Research on analysis optimization and trajectory planning of 3T1R parallel mechanism for coordinate assembly[D]. Harbin: Harbin Institute of Technology, 2021 (in Chinese) [Google Scholar]

[9] YANG Guilin, WU Cuncun, CHEN Qingying, eta al. Kinematics analysis and design optimization of novel 3T1R parallel manipulator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(12): 386–394 [Article] (in Chinese) [Google Scholar]

[10] WU C C, YANG G L, CHEN Q Y, et al. Kinematic design of a novel 4-DOF parallel manipulator[C]//IEEE International Conference on Robotics and Automation, Singapore, 2017: 6099–6104 [Google Scholar]

[11] ZHANG F X, CHEN S L, HE Y Y, et al. A kinematic calibration method of a 3T1R 4-degree-of-freedom symmetrical parallel manipulator[J]. Symmetry, 2020, 12(3): 357 [Google Scholar]

[12] WU Cuncun, YANG Guilin, CHEN Qingying, et al. Kinematic and performance analysis of a 4-DOF 2PPPaR parallel manipulator[J]. Journal of Mechanical Engineering, 2018, 54(3): 36–45 (in Chinese) [Google Scholar]

[13] ANGELES J, CARO S, KHAN W, et al. Kinetostatic design of an innovative schönflies-motion generator[J]. Journal of Mechanical Engineering Science, 2006, 220(7): 935–943 [Google Scholar]

[14] GAUTHIER J F, ANGELES J, NOKLEBY S B, et al. The kinetostatic conditioning of two-limb schönflies motion generators[J]. Journal of Mechanisms and Robotics, 2009, 1(1): 011010 [Google Scholar]

[15] ALTUZARRA O, HERNANDEZ A, SALGADO O, et al. Multiobjective optimum design of a symmetric parallel schönflies-motion generator[J]. ASME Journal of Mechanical Design, 2009, 131(3): 031002 [Google Scholar]

[16] ALTUZARRA O, ŞANDRU B, PINTO C, et al. A symmetric parallel schönflies-motion manipulator for pick-and-place operations[J]. Robotica, 2011, 29(6): 853–862 [Google Scholar]

[17] HERNÁNDEZ A, ALTUZARRA O, SALGADO O, et al. Designing parallel manipulators: from specifications to a real prototype[J]. Industrial Robot, 2012, 39(5): 500–512 [Google Scholar]

[18] LI Hongwei. Workspace and rotation capacity analysis of 4-DOF 3T1R parallel mechanism[J]. Machine Design and Research, 2020, 36(5): 75–80 (in Chinese) [Google Scholar]

[19] LI Xu, LUO Xia, LUO Cheng, et al.. A discrete Monte Carlo approach to workspace analysis of a type of 3T1R parallel mechanism[J]. Machinery, 2020, 47(5): 27–32 (in Chinese) [Google Scholar]

[20] HE Yangtao, MA Chunsheng, WEN Jie, et al. Kinematic analysis and workspace analysis of 2-PCR_-2-UPS parallel mechanism[J]. Science Technology and Engineering, 2023, 23(4): 1481–1487 (in Chinese) [Google Scholar]

[21] HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Higher Space Mechanics[M]. Beijing: Higher Education Press, 2006 (in Chinese) [Google Scholar]

[22] LI Z H, LU Q G, WANG H Z, et al. Design and analysis of a novel 3T1R four-degree-of-freedom parallel mechanism with infinite rotation capability[J]. Journal of Mechanical Engineering Science, 2022, 236(14): 7771–7784 [Google Scholar]

[23] HUANG Zhen, ZENG Daxing. Calculation of degrees of freedom of mechanisms: principles and methods[M]. Beijing: Higher Education Press, 2016 (in Chinese) [Google Scholar]

[24] HAN Jianyou, YANG Tong, YU Jingjun. Higher institutional studies[M]. Beijing: Machinery Industry Press, 2015 (in Chinese) [Google Scholar]

[25] ZHU Dachang, CHEN Dehai, FENG Wenjie. Research on the integrated theory of space configuration and intelligent control of flexible and parallel mechanism[M]. Beijing: Metallurgical Industry Press, 2013 (in Chinese) [Google Scholar]

[26] WANG Shaoxing. Design and analysis of robot structure for battery swapping of electric vehicle[D]. Harbin: Harbin Institute of Technology, 2012 (in Chinese) [Google Scholar]

[27] LU Kai, WAN Xiaojin, LI Qinglei, et al. Workspace analysis and parameter optimization of 8-SPU parallel robot[J]. Machine Tool and Hydraulics, 2018, 46(21): 20–23 (in Chinese) [Google Scholar]

[28] HUANG Guanyu, FANG Yuefa, QU Haibo, et al. Optimization of the motion performance of planer five-bar linkage using a genetic algorithm[J]. Journal of Beijing Jiaotong University, 2015, 39(4): 44–48 (in Chinese) [Google Scholar]