EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 457-466 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 457 - 466
DOI https://doi.org/10.1051/jnwpu/20254330457
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

近年来，复合材料结构因具有较大的比刚度、比强度和良好的可设计性而被广泛用于各个领域[1]。蜂窝夹层结构作为一种典型的复合材料结构，主要由上下2层复合材料蒙皮面板和中间的轻质芯材组成，其网格形式通常有正六边形、方形和菱形等[2]。蜂窝夹层复合材料雷达罩是一种集电气性能、气动外形和特殊功能于一体的结构件，作为雷达设备的电磁窗和保护罩在航空航天等领域中广泛应用[3]。雷达罩一般位于飞机的机头部位，在工作过程中直接暴露在外界环境下，当遇到风、雨和雪等恶劣天气条件时，雷达罩结构很容易受到损坏[4]。这种破坏可能导致雷达罩结构性能下降，进而影响雷达的探测能力和测量精度[5]。因此，对蜂窝夹层复合材料雷达罩结构进行可靠性分析明确其安全水平是非常重要的。

目前，对于蜂窝夹芯复合材料结构的研究不断发展。贺靖等[6]对蜂窝夹层复合材料四点弯曲性能进行了宏观力学和失效模式分析，发现蜂窝芯厚度是影响四点弯曲性能的重要因素。周诗雨等[7]针对蜂窝夹层复合材料构件的固化变形问题，以某L型蜂窝夹层构件为研究对象，分析了蜂窝的几何因素对蜂窝夹层构件的固化变形影响规律。李国举等[8]模拟了鸟体高速撞击蜂窝夹芯天线罩的动态力学响应过程，发现泡沫铝夹心材料在吸能方面起主要作用。李洪年等[9]建立了复合材料蜂窝夹芯结构受冲击后压缩的渐进损伤失效分析模型，并对其进行了可靠性及灵敏度分析。田静等[10]以平稳编织面板蜂窝夹芯结构作为研究对象，利用Kriging代理模型和Monte Carlo法对结构进行了可靠性和全局灵敏度分析。目前对于蜂窝夹芯复合材料雷达罩结构可靠性与灵敏度分析的研究鲜有报道。蜂窝夹芯复合材料雷达罩结构在工作中直接暴露在外界空气中，容易遭到破坏，同时其具有较多输入变量，在进行可靠性与灵敏度分析时难度较大。因此考虑蜂窝夹层复合材料雷达罩结构的失效模式，对其进行可靠性与灵敏度分析具有重要意义。

本文提出了一种蜂窝夹层复合材料雷达罩结构在工作过程中受风载作用下的可靠性与灵敏度分析方法。在Abaqus软件中建立了蜂窝夹层复合材料雷达罩结构的有限元模型，利用Matlab和Abauqs的联合仿真实现了雷达罩结构的参数化。建立BP神经网络代理模型，采用Monte Carlo法计算了结构失效概率和全局灵敏度指标，分析得到对结构可靠性及典型输出响应影响较大的关键变量，可为复合材料雷达罩结构的优化设计提供指导。

1 蜂窝夹层复合材料雷达罩

1.1 雷达罩模型

本文建立的雷达罩有限元模型如图 1所示，该模型分为三部分，即PartⅠ、PartⅡ和PartⅢ。其中PartⅠ和PartⅡ由3层材料组成，为蜂窝夹芯结构；PartⅢ由2层材料组成，为层合板复合结构。该模型共用了3种材料，分别为材料1、材料2和材料3。其中：材料1为层合板复合材料；材料2、材料3为不同的正六边形蜂窝材料。每部分具体信息如下：

thumbnail 图1

雷达罩结构分区与材料属性

1) PartⅠ共3层，第1, 3层为材料1，厚度为8×10-4 m，第2层为材料2，厚度为6×10-3 m，3层的铺层角度都为0°。

2) PartⅡ共3层，第1, 3层为材料1，厚度为8×10-4 m，第2层为材料3，厚度为6×10-3 m，3层的铺层角度都为0°。

3) PartⅢ共2层，每层都为材料1，厚度为3×10-3 m，2层的铺层角度都为0°。

通过对模型的研究以及相关资料的查阅[8, 11]，最终确定该雷达罩结构的输入变量为21个。输入变量Xi(i=1, 2, …, 21)服从正态分布，即Xi~N(μi, σi2)(i=1, 2, …, 21)。变量间均相互独立。输入变量的具体信息如表 1所示。

表1

雷达罩结构输入变量信息

1.2 有限元分析

本文所建立的雷达罩模型为圆顶结构，其底部为圆形结构，直径为1 610 mm，底部圆形中心距顶部的距离为740 mm。模型整体采用壳单元建模，单元类型为S4R，单元个数为980。雷达罩所受风载及约束情况如图 2所示，其中风载分布在雷达罩外表面，雷达罩下部有4个安装孔，分别与机头下部采用固定连接方式，在雷达罩有限元模型中设置为固定约束。利用Abaqus软件对有限元模型进行静强度和模态分析，重点关注的雷达罩结构典型输出响应为最大应力、最大位移、总应变能和一阶固有频率，分析结果如图 3所示。

thumbnail 图2

雷达罩模型受载图

thumbnail 图3

雷达罩结构有限元分析结果

通过对雷达罩结构进行有限元分析，可获取结构的最大应力、最大位移、总应变能和一阶固有频率频率等具体数值, 可靠性与灵敏度分析提供数据支持。

1.3 雷达罩结构屈曲失效分析

雷达罩在工作过程中直接暴露在外部环境中，会受到因风载导致的压缩、弯曲和剪切等外部作用。屈曲是雷达罩在这些载荷作用下最常见的失效模式之一[12]。根据1.2节中的载荷情况，对雷达罩结构有限元模型进行屈曲分析，可为接下来屈曲失效准则的建立提供必要的数据支持。

在本文中，施加在雷达罩有限元模型中的载荷记为F0，通过有限元分析得到的屈曲特征值记为λ1。屈曲临界载荷记为F*，它是施加在模型上的载荷F0与屈曲特征值λ1的乘积，即F*=λ1F0。雷达罩遭受的实际载荷记为FA，由于雷达罩在工作过程中面对着复杂的外界环境，FA充满着不确定性，因此在本文中假定其服从正态分布，即FA~N(μ1, σ12)。引入风载系数λ2使其满足FA=λ2F0，则此时λ2也服从正态分布，即λ2~N(μ2, σ22)。建立雷达罩的屈曲失效准则如(1)式所示

式中: X={X1, X2, …, Xn}为输入变量；当g≤0认为失效发生，当g>0时认为失效未发生。

2 可靠性及灵敏度分析

2.1 参数化建模

本文利用Abaqus软件建立了蜂窝夹层复合材料雷达罩结构的有限元分析模型，并利用Matlab语言进行二次开发，实现了雷达罩结构模型的参数化。其具体步骤如下：

1) 提取Abaqus有限元模型中的.inp文件。

2) 确定输入变量信息，基于Matlab语言，读取并修改上一步生成的.inp文件。

3) 将步骤2)生成的.inp文件提交至Abaqus进行计算，得到相应的输出响应。

4) 编写后处理Python脚本，提取Abaqus计算后得到.odb结果文件中的数据。

2.2 神经网络

2.2.1 神经网络代理模型

可靠性与灵敏度分析过程将多次调用有限元模型，导致其计算效率较低。本文利用BP神经网络(back propagation neural network)[13]替代原有限元模型进行分析计算，从而提高计算效率。BP神经网络的拓扑结构如图 4所示。

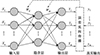thumbnail 图4

BP神经网络拓扑结构

在图 4中，Xi(i=1, 2, …, n)表示n个神经网络的输入值；隐含层的数量用p来表示，Oj(j=1, 2, …, p)表示隐含层神经元；Yk(k=1, 2, …, m)表示m个神经网络预测输出值。yk(k=1, 2, …, m)表示m个真实输出值。Wij表示输入层到隐含层的连接权重，Wjk表示隐含层到输出层的连接权重。隐含层和输出层的每个输入可由(2)~(3)式计算。

均方误差(mean square error, MSE)EMS常被用来估计神经网络的精度，其公式为

式中：N为样本数；Yi和yi分别为预测输出向量和真实输出向量。测试集拟合优度R常被用来测量预测输出和真实输出之间的相关性，其被定义为

式中：y为真实输出的均值向量。R越靠近于1表示神经网络的精度越高，一般R>0.95时表明精度符合要求，本文中神经网络代理模型构建可参考文献[14]。

2.2.2 代理模型的构建

本文针对雷达罩结构的不同输出响应一共建立了3个神经网络代理模型, 分别为基于最大应力、最大位移和总应变能的代理模型Sur-Ⅰ, 基于一阶固有频率的代理模型Sur-Ⅱ, 基于屈曲失效特征值的代理模型Sur-Ⅲ。

在代理模型Sur-Ⅰ的构建中, 输入层节点数为21, 对应表 1中描述的21个输入变量; 隐含层节点数为5;输出层节点为3, 对应3个输出变量即最大应力、最大位移和总应变能。误差限设定为1×10-4, 神经网络在经过399次迭代后开始收敛, 训练过程终止。均方误差EMS的收敛历史及测试集拟合优度R如图 5所示, 其中R为0.999 33, 表示神经网络的精度满足要求。

thumbnail 图5

神经网络误差

代理模型Sur-Ⅰ、Sur-Ⅱ和Sur-Ⅲ的训练信息如表 2所示, 其精度均符合要求。

表2

代理模型信息

2.2.3 基于方差的全局灵敏度指标

基于方差的全局灵敏度指标(即Sobol指标)由Sobol等[15]利用方差分解(analysis of variance, ANOVA)的思想提出, 具有通用性强、反映输入变量整个变化范围对输出性能方差等优点。假设结构的功能函数为Y=g(X), 其中X =(X1, X2, …, Xn)表示n维独立的输入变量, 可将功能函数Y=g(X)分解为

式中: g0为函数g(X)均值。对(6)式求方差可得

主方差贡献表示当输入变量Xi固定时g(X)的方差改变量, 定义为

式中: E[V (g(X) Xi)]为当输入变量Xi固定时其余输入变量对总方差的贡献。总方差贡献为当Xi不固定, 但其余变量均固定时, 输入变量Xi对g(X)方差的贡献, 定义为

式中: X~i为输入变量X中除Xi外的n-1维向量。

基于方差的全局灵敏度指标中主测度指标SM和总测度指标ST可由(10)~(11)式定义。

2.3 失效概率及基于失效概率的全局灵敏度指标

2.3.1 失效概率

在结构可靠性分析理论中, 结构是否失效用极限状态函数来判断, 其定义如(1)式所示。极限状态函数将输入变量空间分为失效域F={ X : g(x)≤0}和安全域S={ X : g(x)>0}两部分。g(x)≤0时的概率, 即为结构的失效概率Pf, 可由(12)式来表示。

式中: fX(x)为随机输入变量的联合概率密度函数。(12)式可进一步由(13)式表示。

式中: Rn为n维输入变量空间; E[·]为期望算子; IF(x)为失效域的指示函数, 当g(x)≤0时, IF(x)=1, 否则IF(x)=0。(13)式为失效概率可转化为指示函数期望的形式, 它可由Monte Carlo法进行估计，如(14)式所示。

式中: N为样本总数; NF为落入失效域内的样本数。

2.3.2 基于失效概率的全局灵敏度指标

相较于基于偏导数的局部可靠性灵敏度分析, 基于失效概率的全局灵敏度能够更加全面衡量输入变量对结构失效概率的平均影响[16]。输入变量Xi对失效概率Pf的全局灵敏度指标可由(15)式定义。

式中: Pf|xi为当输入变量Xi被固定在名义值xi处的条件失效概率。输入变量的δi指标越大, 表示该变量对结构失效概率的影响越大。

2.4 基于BP神经网络的蜂窝夹层复合材料雷达罩结构失效概率及灵敏度分析过程

本文基于代理模型技术和Monte Carlo法对蜂窝夹层复合材料雷达罩结构进行了可靠性及灵敏度分析, 图 6为分析流程图，基本过程如下。

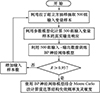thumbnail 图6

失效概率及灵敏度分析流程图

步骤1  抽取样本。采用拉丁超立方抽样生成500组输入变量样本。

步骤2  计算模型响应。利用参数化模型, 计算500组输入下的模型响应值。

步骤3  训练神经网络。利用500组输入-输出数据构建BP神经网络代理模型。

步骤4  判断代理模型的精度。若测试集拟合优度R>0.95, 代理模型精度符合要求, 否则返回步骤1增加输入变量样本数。

步骤5  计算失效概率及灵敏度。通过已建立的BP神经网络代理模型结合Monte Carlo法计算雷达罩结构的失效概率及灵敏度。

3 结果分析

3.1 雷达罩结构基于典型输出特征的全局灵敏度指标

本文以雷达罩结构的4种典型输出特征为输出响应进行全局灵敏度分析, 同时为了研究输入变量的变异系数(coefficient of variation, CoV)对结构输出响应全局灵敏度指标的影响, 计算了输入变量在5组变异系数(0.02, 0.04, 0.06, 0.08, 0.1)下的全局灵敏度指标, 包括基于方差的全局灵敏度指标SM和ST, 计算结果如图 7~10所示。

thumbnail 图7

基于最大应力的全局灵敏度计算结果

thumbnail 图8

基于最大位移的全局灵敏度计算结果

thumbnail 图9

基于总应变能的全局灵敏度计算结果

thumbnail 图10

基于一阶固有频率的全局灵敏度计算结果

以雷达罩结构的最大应力为输出响应进行全局灵敏度分析, 结果如图 7所示。由图 7a)~7b)中最大应力的基于方差的全局灵敏度指标SM和ST可知, 2种指标下变量的重要性排序结果基本相同。不同的变异系数对变量的指标值的大小影响较小, 且基本不影响变量的重要性排序。在每组变异系数下, 变量X2(Mat1E22, 材料1的22向模量)的指标值最大, 说明该变量对最大应力的影响最大。其次是变量X21(M3, 层压背衬厚度2)和变量X1(Mat1E11, 材料1的11向模量)。在雷达罩结构最大应力的分析过程中, 应重点关注变量X2, X21和X1等, 以有效地改善结构的最大应力。

以雷达罩结构的最大位移为输出响应进行全局灵敏度分析, 结果如图 8所示。由图 8a)~8b)中全局灵敏度指标SM和ST可知, 2种指标下变量的重要性排序结果相同。变异系数对2种指标值的大小影响较小, 且基本不影响变量的重要性排序。在每组变异系数下, 变量X2(Mat1E22, 材料1的22向模量)对最大位移的影响最大。其次是变量X21(M3, 层压背衬厚度2)和变量X1(Mat1E11, 材料1的11向模量)。在雷达罩结构最大位移的分析过程中, 应重点关注变量X2, X21和X1等, 以便更有效地改善结构的最大位移。

由图 9a)~9b)中总应变能的基于方差的全局灵敏度指标SM和ST可知, 2种指标下变量的重要性排序结果相同。不同的变异系数基本不影响变量的重要性排序。在每组变异系数下, 变量X1(Mat1E11, 即材料1的11向模量)对总应变能的影响最大, 其次是变量X2(Mat1E22, 即材料1的22向模量)、变量X19(M1, 即层压背衬厚度1)和变量X3(Mat1G12, 即材料1的12向的模量)。在雷达罩结构总应变能的分析过程中, 应重点关注变量X1, X2, X19和X3, 以便更有效地改善结构的总应变能。

由10a)~10b)中一阶固有频率基于方差的全局灵敏度指标SM和ST可知, 2种指标下变量的重要性排序结果相同。变异系数基本不影响变量的重要性排序。在每组变异系数下, 变量X6(Mat1Ro, 材料1的密度)的指标值最大, 说明该变量对一阶固有频率的影响最大, 其次是变量X19(M1, 层压背衬厚度1)和变量X2(Mat1E22, 材料1的22向模量)。在分析雷达罩结构一阶固有频率的分析过程中, 应重点关注变量X6, X19和X2, 以便更有效地改善结构的一阶固有频率。

对结构的典型输出特征值影响较大的前3个输入变量如表 3所示。由表 3可以看出, 对结构的典型输出影响最大的变量分别是Mat1E22, Mat1E22, Mat1E11和Mat1Ro, 变量均与材料1有关, 因此在进行结构设计时应重点关注材料1的基本力学性能。

表3

变量重要性排序汇总

3.2 雷达罩结构失效概率

为了研究风载大小和变异系数对结构失效概率的影响, 本文计算了风载系数λ2的均值μ2在区间[1, 4]内(取值间隔为0.5)变化时和变异系数取不同值(0.05, 0.1, 0.15, 0.2, 0.25)时的结构失效概率。失效概率的求解方法为Monte Carlo法, 样本个数为5×105。雷达罩结构的失效概率计算结果如图 11所示。从图 11中可看出, 在不同的风载变异系数下, 失效概率随风载系数λ2均值μ2的增大而增大; 当μ2一定时, 随着变异系数的增大, 结构失效概率也在逐渐增大; 当风载变异系数一定时, 失效概率随着μ2的增大而增大, 且在μ2为1~2时, 结构处于绝对安全状态, 当μ2为3~4时结构失效概率急剧增大。

thumbnail 图11

雷达罩结构失效概率

3.3 雷达罩结构基于失效概率的全局灵敏度指标

从3.2节可看出, 当风载系数λ2均值μ2为3~4时结构失效概率急剧增大。选择当μ2为3.5时, 对雷达罩模型进行基于失效概率的全局灵敏度分析, 结果如图 12所示。从图 12可看出, 随着风载变异系数的增大, 全局灵敏度指标相应的增大, 两者呈现出明显的正相关。各个变量对应的灵敏度指标的相对大小保持不变, 这说明变异系数的大小虽影响全局灵敏度指标的大小, 但不影响变量的重要性排序结果。在每组变异系数下, 变量X20(M2, 蜂窝夹层厚度)重要性最高, 其次是变量X16(Mat3G13, 材料3的13向模量)和变量X19(M1, 层压背衬厚度1)。

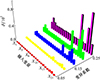thumbnail 图12

基于失效概率的全局灵敏度指标

4 结论

本文对蜂窝夹层复合材料雷达罩结构进行了有限元分析和可靠性及灵敏度分析，明确了雷达罩结构的安全水平，得到了对结构可靠性及关键输出响应影响较大的关键变量，为后续的优化设计提供了指导。

1) 在雷达罩结构典型输出特征的全局灵敏度分析中，4种灵敏度指标下变量的重要性排序基本相同，输入变量的变异系数基本不影响输入变量的重要性排序，对结构的典型输出影响较大的变量分别为Mat1E22, Mat1E22, Mat1E11和Mat1Ro。

2) 基于屈曲失效模型，计算了结构失效概率和基于失效概率的全局灵敏度指标。对结构失效概率影响较大的前3个变量为M2, Mat3G13和M1。当变异系数一定时，失效概率随着λ2的增大而增大；载荷变异系数对于变量对结构失效概率的重要性排序基本无影响。

在未来的研究中进一步探索雷达罩可能的失效模式及高效的可靠性与灵敏度分析计算方法，是值得研究的方向。

References

  1. YUE Zhufeng, WANG Fusheng, WANG Peiyan, et al. Structural analysis and optimal design of aircraft composite matersials[M]. Beijing: Science Press, 2011 (in Chinese) [Google Scholar]
  2. MA Chao, GU Zhiyue, CAO Yuhao, et al. A method of foam weight reduction for spacecraft honeycomb sandwich panel[J]. Journal of Astronautics, 2022, 43(7): 957–963 (in Chinese) [Google Scholar]
  3. LI Huan, LIU Jun, XIAO Jiayu, et al. An overview on the technology and electectromagnetic performance of radome[J]. Materials Reports, 2012, 26(8): 48–52 (in Chinese) [Google Scholar]
  4. WANG Xuan, WANG Hongda, GUO Qiaorong, et al. Study of allowable damage in honeycomb sandwich structure radomes[J]. Science and Technology & Innovation, 2018, 4: 1–3 (in Chinese) [Google Scholar]
  5. MANCINI A, LEBRON R M, SALAZAR J L. The Impact of a wet S-band radome on dual-polarized phased-array radar system performance[J]. IEEE Trans on Antennas and Propagation, 2019, 67(1): 207–220 [Google Scholar]
  6. HE Jing, SUN Chaoming, YIN Hang, et al. Study on four-point bending performance and failure modes of honeycomb sandwich composite materials[J]. Hi-Tech Fiber and Application, 2023, 6: 26–33 (in Chinese) [Google Scholar]
  7. ZHOU Shiyu, AN Luling, ZHAO Cong, et al. Research on influence of structural factors on curing deformation of honeycomb sandwich components[J]. Machine Building & Automation, 2023, 52(4): 96–100 (in Chinese) [Google Scholar]
  8. LI Guoju, ZHANG Qianrui, HOU Huidong, et al. Simulation research on anti-brid impact performance of honeycomb sandwich radome[J]. Journal of Zhengzhou University of Aeronautics, 2024, 41(1): 36–42 (in Chinese) [Google Scholar]
  9. LI Hongnian, SHI Qiangbin, WANG Xuan, et al. Reliability and sensitivity anslysis of compressive strength after low-speed impact for composite honeycomb sandwich structure[J]. Composites Science and Engingeering, 2024, 14(2): 5–12 (in Chinese) [Google Scholar]
  10. TIAN Jing, ZOU Runwen, WANG Xuan, et al. Reliability and sensitivity analysis of edgewise compressive strength for plain woven faceplate honeycomb sandwich structure[J]. Composites Sciense and Engineering, 2022, 12(7): 17–23 (in Chinese) [Google Scholar]
  11. JI Pihua, YU Jixuan, WANG Peng. Structure design technology of radar radome[J]. Journal of Machine Design, 2023, 40(suppl.2): 114–118 (in Chinese) [Google Scholar]
  12. SUN G, HUO X, CHEN D, et al. Experimental and numerical study on honeycomb sandwich panels under bending and in-panel compression[J]. Materials and Design, 2017, 133: 154–168 [Google Scholar]
  13. GOH A T C. Back-propagation neural networks for modeling complex systems[J]. Artificial Intelligence in Engineering, 1995, 9(3): 143–151 [Google Scholar]
  14. LI J, CHENG J H, SHI J Y, et al. Brief introduction of back propagation(BP) neural network algorithm and its improvement[J]. Advances in Intelligent and Soft Computing, 2012, 2(169): 553–558 [Google Scholar]
  15. SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1/2/3): 271–280 [Google Scholar]
  16. BORGONOVO E, PLISCHKE E. Sensitivity analysis: a review of recent advances[J]. European Journal of Operational Research, 2016, 248(3): 869–887 [Google Scholar]

All Tables

表1

雷达罩结构输入变量信息

In the text
表2

代理模型信息

In the text
表3

变量重要性排序汇总

In the text

All Figures

thumbnail 图1

雷达罩结构分区与材料属性
In the text
thumbnail 图2

雷达罩模型受载图
In the text
thumbnail 图3

雷达罩结构有限元分析结果
In the text
thumbnail 图4

BP神经网络拓扑结构
In the text
thumbnail 图5

神经网络误差
In the text
thumbnail 图6

失效概率及灵敏度分析流程图
In the text
thumbnail 图7

基于最大应力的全局灵敏度计算结果
In the text
thumbnail 图8

基于最大位移的全局灵敏度计算结果
In the text
thumbnail 图9

基于总应变能的全局灵敏度计算结果
In the text
thumbnail 图10

基于一阶固有频率的全局灵敏度计算结果
In the text
thumbnail 图11

雷达罩结构失效概率
In the text
thumbnail 图12

基于失效概率的全局灵敏度指标
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.