| Issue |
JNWPU
Volume 43, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 163 - 170 | |
| DOI | https://doi.org/10.1051/jnwpu/20254310163 | |
| Published online | 18 April 2025 | |
Wear reliability analysis of tapered valve based on second moment of checking point
基于验算点二阶矩的锥形活门磨损可靠性分析方法
1
AVIC China Aero-Polytechnology Establishment, Beijing 100028, China
2
School of Construction Machinery, Chang'an University, Xi'an 710064, China
3
Beijing Power Machinery Institute, Beijing 100074, China
Received:
7
December
2023
In order to clarify the influence of the wear characteristics on the reliability of the conical valve in the fuel system of an aero-engine, a second-order moment reliability analysis method based on the checking point was proposed, which focuses on the influence of the key parameters on the wear reliability of the conical valve on the basis of establishing the wear depth model of the conical valve. Combining the Archard wear model with the spool force analysis, the mapping relationship between the cumulative wear depth of the valve and the geometry, material parameters, and working condition parameters was established, and the wear function was clarified and the basic random variables were determined through the generalized stress-interference theory. Through the proposed second-order moment reliability analysis method at the check point, the wear reliability and sensitivity of a conical valve were simulated and analyzed. The simulation results show that the wear reliability is positively correlated with the material hardness of the conical valve at a certain cone angle, and increasing the diameter of the valve has a more obvious effect on the wear reliability. The wear reliability is slightly improved by increasing the number of cone angles. Moreover, the variables that have positive and negative effects on the wear reliability of the conical valve are identified through the global sensitivity analysis, and the sensitivity ranking of importance and dispersion is clarified.
摘要
为了明确航空发动机燃油系统中磨损特性对其锥形活门的可靠性影响规律, 提出了一种基于验算点的二阶矩可靠性分析方法, 重点在建立锥形活门磨损深度模型基础上分析关键参数对锥心活门磨损可靠度的影响规律。结合Archard磨损模型与阀芯受力分析, 建立活门累积磨损深度与几何尺寸、材料参数、工况参数间的映射关系, 通过广义应力-干涉理论明确磨损功能函数并确定基本随机变量。采用所提出的验算点二阶矩可靠性分析方法, 对某锥形活门磨损可靠性及灵敏度进行仿真分析。仿真结果表明: 在锥角一定时, 磨损可靠度与锥形活门材料硬度呈正相关关系, 活门直径大小对磨损可靠度影响较为明显; 增大锥角度数, 磨损可靠度将有小幅提升; 通过分析全局灵敏度确定了对锥形活门磨损可靠性产生正、负向影响的变量, 并明确了重要度和分散性的敏感性排序。
Key words: tapered valve / wear / second moment / reliability / sensitivity
关键字 : 锥形活门 / 磨损 / 二阶矩 / 可靠度 / 灵敏度
© 2025 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
随着新一代航空推进技术向宽域大包线、超机动、自适应循环等技术方向发展，进一步要求燃油系统必须保证高性能及高稳定性供油，而高可靠、长寿命燃油系统的研发更是实现航空发动机技术革新的重要标志[1–2]。其中，锥形活门是燃油系统主要的控制元件之一，由锥形活门阀芯和阀座相互配合实现燃油的通断控制，可作为燃油调节器的安全活门等功能零件使用，锥形活门的可靠性及寿命问题严重影响着燃油系统的平稳安全运行[3–4]。然而，由于特殊的运行载荷，如高温、高压、高速等要求，锥形活门的阀芯和阀座等会产生无法避免的相互运动，进而导致粘着磨损等故障，而磨损是锥形活门典型故障模式之一，影响着燃油调节器及整个发动机系统的寿命及可靠性[5–6]。因此，有必要开展锥形活门磨损可靠性分析方法的研究工作，这对发动机系统可靠性的提升具有一定的理论及工程价值。然而，当前燃油系统可靠性设计并未形成正向且完善的体系，导致了各种故障问题产生，尤其是一些典型的机械产品耗损性故障问题突出且复杂，锥形活门的粘着磨损便是其中之一。在锥形活门的磨损形成过程中，由于外部环境载荷严酷且运行边界不确定性明显，其磨损机理受因较广，建立高精度的磨损机理数学模型更是难点之一[7]。因此，很有必要开展锥形活门的磨损可靠性分析方法研究，确定反映锥形活门磨损特性的建模方法、建立锥形活门的磨损可靠性分析方法、明确影响锥形活门磨损可靠性的定量关系及变量灵敏度等。
针对磨损特性的相关仿真分析取得了大量的研究成果，包括：磨损模型建模方法、磨损可靠性分析方法等。高涵[8]基于干摩擦磨损实验，研究了摩擦条件对PEEK材料摩擦磨损性能的影响并建立了修正的Archard模型，通过有限元方法建立了对应的磨损有限元数值模拟方法, 并进一步探讨了基于能量法磨损模型在PEEK材料上应用的有效性和合理性。刘先升[9]探究了具有PVD镀层和无镀层的热成形模具钢试样在冲击作用后表面的磨损情况, 并对比分析了各自的表面热机磨损程度，结合Archard磨损理论建立了实际冲击-滑移-保压的有限元仿真模型，获得磨损深度与冲击次数的拟合关系，与实际实验样块表面磨损深度的实验数据进行对比分析，并进行了准确性校核。董书娜等[10]根据刷式密封结构特点构建了刷丝磨损量关于时间的一阶线性非齐次微分方程，并基于Archard模型得到刷丝磨损量、磨损率计算的数学模型，研究了结构和工况参数对磨损量和磨损率的影响规律，并分析了结构参数对刷式密封磨损特性影响的灵敏度。李玲等[11]通过引入随温度变化的磨损系数来修正能量耗散磨损模型，基于柱面/平面微动实验建立微动磨损的温度-位移耦合有限元模型，并与Archard模型进行对比，得到了材料塑性、温度和微动循环次数对接触表面磨损和温升的影响。上述成果专门对磨损模型建模方法进行了研究。可见很多科研人员通过Archard磨损模型进行了磨损机理的分析。随着机械产品可靠性得到了越来越多的重视，磨损可靠性分析方法及其在机械产品磨损可靠性仿真方面的应用得到了一定研究。
综上所述，机械产品使用中无法避免地会出现一定程度的磨损问题，并造成系统的性能衰退或产生其他负面影响，定量地进行机械产品的磨损可靠性演变规律描述非常重要。然而，上述研究均未针对航空燃油调节器中的锥形活门开展相关磨损机理的数学建模方法研究，同时，并未涉及锥形活门的磨损可靠性分析方法。因此，本文针对锥形活门开展磨损深度模型建模方法、锥形活门磨损可靠性分析方法、锥形活门磨损可靠性影响规律及灵敏度计算等研究工作。
1 锥形活门磨损深度模型建模方法
1.1 Archard磨损模型
锥形活门在燃油调节器中作为安全活门等被广泛使用。由于严格的边界工况、严酷的运行环境，锥形活门在使用中存在各种复杂的故障模式，而磨损便是其中主要且典型的故障模式之一，严重影响着燃油调节器的寿命及可靠性。其中，粘着磨损被广泛地用于描述摩擦副间滑动造成的磨损，该磨损形式是锥形活门阀芯和阀座之间发生的主要磨损形式。
Archard模型由摩擦学专家J F Archard提出，该模型给出的磨粒磨损演变机理是将磨损过程当作硬质颗粒在固体壁面产生相对滑动，其基本表达式为
式中：V为磨损体积; K为磨损系数; F为接触面法向压力; H为材料硬度; L为相对滑动距离。
(1) 式所示的Archard模型将接触面法向压力、相对滑动距离与材料表面硬度作为主要因素, 其他影响磨损的次要因素在磨损系数K中进行考虑。由于接触面受力情况会产生变化, (1)式可写成微积分形式, 即
假设磨损形成的磨损截面近似为矩形, 令
式中: W为磨损深度; A为接触面积; σ为接触面法向应力; μ为相对滑动速度; t为接触时间。
将(3)式代入(1)式，可得
通过上述公式, 完成锥形活门磨损深度模型建模。
1.2 锥形活门受力分析
为了给定锥形活门的磨损失效判据, 建立了磨损深度模型。在Archard磨损模型, 对锥形活门进行受力平衡分析, 确定其磨损体积与磨损深度的映射关系, 得到锥形活门的磨损深度计算模型。
首先, 对活门阀芯进行受力分析, 阀芯受到作用于锥端的液压力p、尾端的弹簧预紧力Fs、锥体外表面沿周向均匀分布的正压力qN及与阀芯做相反运动的摩擦力qF。其中, qN和qF是阀芯与阀座相互接触的表面力。
当液压力p大于弹簧预紧力Fs时, 锥形阀芯与阀座不接触, 阀门开启, 此时正压力与摩擦力均为零; 当液压力p不大于弹簧预紧力Fs时, 阀芯与阀座相接触, 阀门关闭, 并满足(5)式所示的受力平衡方程。
式中, α为活门锥角, 2个积分项分别为对应圆周长s的正压力和摩擦力在水平方向的投影, 且有
式中: d为圆周直径; f为摩擦因数。
液压力p为压强ps和相应受力面A的乘积, 结合(6)~(7)式计算结果, 代入(5)式, 可得正压力qN为
根据上述分析, 可得所有正压力的合力N为
1.3 锥形活门磨损深度模型
由锥形阀芯的几何结构, 对磨损体积进行推导。图 1为阀芯的轴向剖面结构图, 在阀芯与阀座接触过程中, 磨损掉的部分可视为一环状体, 磨损最深处的深度为h, 设该部分的体积为V, 则V可表示为圆台体积V1与柱体体积V2(图中未标出)之差。
 |
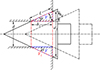图1 阀芯轴向剖面结构 |
由图 1中的几何关系可得
将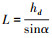 
代入Archard磨损量计算式中, 同时令Va=V, F=N, 可得关于hd的方程, 即
得到
考虑到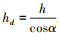 
, 并设阀门闭合次数为m, 可得累积磨损深度
基于Archard磨损模型建模，结合锥形活门的受力分析、几何结构下的磨损体积推导等, 完成锥形活门磨损深度模型建模工作。
2 锥形活门磨损可靠性分析方法
2.1 基于应力-强度干涉的功能函数
以锥形活门的磨损深度为失效判据, 根据应力-强度干涉理论建立相应的极限状态函数, 为
式中: hT为磨损深度最大容许值; h为当前磨损深度, 由(15)式计算得出。x为基本随机变量构成的向量, 当活门的闭合次数一定时, 有
确定a包含的各分量的概率分布类型和分布参数是分析活门磨损可靠性的基础。受经济因素和实际条件制约, 采用类似产品数据对所需数据进行近似估计, (17)式所涉及基本变量包括: 几何尺寸参数、材料性能参数、工况参数等。上述变量分布按选取为规则: 对于尺寸参数而言, 其分布符合正态分布, 名义尺寸可看做其均值, 同时标准差可视为公差数值的1/3;对于材料性能参数, 大量金属材料试验数据统计都表明, 这些参数也多服从正态分布; 考虑到稳态工况下参数的小范围波动, 工况参数也可视为正态分布。
2.2 基于验算点二阶矩可靠性分析方法
基于验算点二阶矩可靠性分析方法是将极限状态函数在设计验算点或最可能失效点(即: 点P*)处展开成泰勒级数, 进而实现近似解析求解的一种可靠性参数计算方法。具体步骤如下:
设影响结构可靠度的n个基本随机变量(如直径、材料硬度等)为xi(i=1, 2, …, n), 可记为一基本随机参数向量x=[x1, x2, …xn]。μxi和σxi为xi的均值和标准差(分别为对原点的一阶矩和二阶中心矩), 具体以(16)式所示的锥形活门极限状态方程为对象对应的极限状态函数为
相应的极限状态方程为
选择失效界面上的某点P*(x1*, x2*, …, xn*), 在该点将极限状态函数泰勒展开, 略去二次以上的项, 得到点P*处的近似线性化极限状态方程为
相应的极限状态函数均值与标准差分别为
式中，ρij为xi与xj的相关系数。由于假设了P*点在失效界面上, 故满足极限状态方程, 即g(x1*, x2*, …, xn*)=0, g的均值可写作
根据可靠度系数β的定义, 有
定义系数λi表示变量xi对σg的贡献, 有
将λi代入(24)式中, 可得
若各随机变量的概率分布均为正态分布, 则所求的可靠度R和失效概率Pf分别为
若某些随机变量不遵循正态分布, 对非正态随机变量可作“当量正态化”处理。具体实现方法此处不做针对性叙述。在具体计算时, 由于P*点在求解前是未知的, β应采用迭代法求解。迭代步骤如下:
1) 选取初值, 通常取xi*=μxi;
2) 由(25)式计算λi;
3) 记xi*=μxi-βλiσxi;
4) 将xi*的表达式代入极限状态方程(19)式中, 解出β;
5) 将β值返回至步骤3)中, 求得xi*的新值;
6) 用新的xi*值重复计算步骤2)~4), 直至β与上一次的差值满足精度要求。此时, 求出的β即可用于求解可靠度或失效概率。
3 结果与分析
3.1 可靠性计算结果
按正态分布对(17)式中涉及的各基本随机变量进行统计, 结果见表 1。其中, 阀芯直径d、材料硬度H和锥角α是可控的随机变量, 表中只给出了基准量。此外, c为变异系数, 是标准差与均值之比。f和K是相关随机变量, 将二者之间的相关系数近似定为0.6。
锥形活门基本随机变量统计数据
基于所提出的验算点二阶矩方法对锥形活门的磨损可靠性进行分析。图 2为在不同材料硬度下(分别为320, 580, 882 HB), 锥形活门直径对磨损可靠度的影响规律结果。
 |
图2 锥形活门直径对磨损可靠度的影响规律 |
可以看出, 采用验算点法能较准确地实现磨损可靠性分析。在其他参数一定的情况下, 磨损可靠度同活门材料的硬度之间呈正相关关系, 若能在现有条件下改进材料硬度, 将进一步提升活门的磨损可靠性; 另外, 在一定范围内, 活门直径大小对磨损可靠度影响较为显著, 增大活门直径对于提升磨损可靠性意义较大, 但继续增大直径至一定数值后, 可靠度提升并不明显。
以上结果均建立在锥角一定的条件下, 无法反映锥角变化时, 活门直径对磨损可靠度的影响规律。因此, 采用所提出的分析方法, 在材料硬度一定时, 分析锥角与活门直径同时改变对磨损可靠度的影响规律, 当材料硬度为580 HB, 且其他参数一定时, 增大锥角度数, 磨损可靠度将有小幅提升; 另外, 一定范围内, 增大活门直径对于磨损可靠度的提升作用比增大锥角更为显著。
3.2 灵敏度分析结果
对锥形活门的磨损可靠性进行灵敏度分析, 可获取磨损可靠度与各个基本随机变量分布参数波动间的量化关系, 分析各变量分布参数对磨损可靠性影响程度的主次关系。此处, 分别分析其对局部灵敏度和全局灵敏度影响规律。
首先, 在验算点二阶矩方法求解基础上, 对锥形活门磨损可靠性局部灵敏度进行求解分析。将锥形活门的磨损可靠性局部灵敏度定义为可靠度R对基本随机变量均值μxi、标准差σxi的偏导数, 即均值灵敏度和标准差灵敏度分别为
基于验算点二阶矩方法进行磨损可靠度分析时, 通过给定表 1所示的各随机变量分布参数, 将最终迭代出的验算点代入(28)~(29)式中, 即可得到磨损可靠性在相应分布参数取值点处的局部灵敏度, 结果见表 2。
锥形活门磨损可靠性局部灵敏度
表 2中, 在活门直径均值6 mm附近, 直径增加微小量值Δd, 可靠度相应增大1.3Δd; 同时, 锥角增加微小值Δα, 可靠度增大0.004 32Δα。尽管直径同锥角度数的量纲不同, 0.004 32Δα与1.3Δd无法直接比较, 但若直径、锥角的微小增量(Δd、Δα)分别对应各自均值相同幅度增量, 如均为均值的2%, 则可靠度随直径的变化更为敏感。同时, 根据标准差灵敏度计算结果来看, 在给定的标准差取值点附近, 基本变量标准差的波动变化对活门磨损可靠度的影响较小。
其次, 进一步对锥形活门磨损可靠性的全局灵敏度进行求解分析。全局灵敏度是指在整个变量分布参数取值区间上的灵敏度, 是分布参数的函数形式。全局灵敏度在可靠性灵敏度分析中比局部灵敏度应用更为广泛, 用于衡量模型输入变量的不确定性在其整个分布区域内对输出响应的不确定性影响。显然, 全局灵敏度可以通过求得一系列离散点处的局部可靠性灵敏度来给出。当基本变量分布参数θ的定义域为[θ1, θ2]时, 视其服从定义域上的均匀分布是合理的, 设分布密度函数为f(θ), 将全局灵敏度函数记为S(θ), 则全局灵敏度函数期望E和方差D分别为
考虑到各变量方差对可靠度的影响都较小, 故只对均值灵敏度特征指标进行计算。根据上述方法, 依次取θ为各变量均值, 应用验算点二阶矩方法得出样本点并进行灵敏度计算, 进而由(30)~(31)式得出全局灵敏度函数特征指标, 结果见表 3。表 3中, 在所有对可靠性产生正向影响的变量中, 按重要程度排序, 依次为ps, f, d, hT, α, H。此外, 对可靠性产生负向影响的2个变量中, 磨损系数K的影响程度大于预紧力Fs。从分散性来看, 活门直径d和压强ps对可靠性的影响程度具有较大的波动性。
锥形活门磨损可靠性全局灵敏度
因此, 在活门所处环境不变时, 即液压力和预紧力无法改变的情况下, 通过改变活门尺寸参数、改进材料和加工等途径可以改善活门的抗磨损性。但在改变直径时, 需对可靠度进行计算验证, 以确定当前直径对可靠度提升的有效性。
图 3为不同随机变量d, ps, Fs的全局灵敏度函数仿真结果。
 |
图3 全局灵敏度函数仿真结果 |
从图 3可看出各变量均值和标准差的变化对活门磨损可靠度的影响方向和影响程度。图 3a)中，活门直径均值大小对可靠度的影响始终是正向的，即直径均值增大，可靠度也随之增大，但在活门直径均值增大到一定值后，进一步增大活门直径对可靠度的增大作用可以忽略不计，与前文分析一致。因此，若活门直径处于一定范围之内，如图中的5.5~6.5 mm，可通过增大直径的方式来增大可靠性，若当前活门直径已超出该范围，则不建议通过增大直径的方式提升活门的磨损可靠性。另外，图 3b)中，活门直径的标准差对可靠度有着小幅度的负向影响，提升加工精度，尽量减少直径的偏差对磨损可靠度的提升也有一定意义。
图 3c)~3d)分别给出了压强ps对全局灵敏度的仿真曲线，可以看出压强增大，对磨损可靠度影响产生了一定效果，但影响效果逐渐降低。图 3e)~3f)分别给出了预紧力Fs对全局灵敏度的仿真曲线，可见预紧力对磨损可靠度产生的影响为负影响，与表 3结果一致。
4 结论
为了深入确定航空发动机燃油系统中锥形活门的磨损可靠性，基于Archard磨损模型和锥形活门的受力分析，建立了锥形活门的磨损深度模型；在应力-强度干涉方法基础上，提出了基于验算点二阶矩可靠性分析方法，并以某型燃油系统锥形活门为例，采用所提出的分析方法进行了可靠性仿真分析及灵敏度计算。主要结论如下：
1) 采用提出的验算点法能准确地实现磨损可靠性分析。在其他参数一定的情况下，磨损可靠度同活门材料的硬度之间呈正相关关系；另外，在一定范围内，活门直径大小对磨损可靠度影响较为显著，但增大直径至一定数值后，可靠度提升并不明显；
2) 根据局部灵敏度计算结果可以看出：可靠度随活门直径的变化更为敏感。根据标准差灵敏度计算结果可以看出在给定的标准差附近，各基本变量标准差的波动变化对活门磨损可靠度的影响较小；
3) 根据全局灵敏度计算结果可以看出，压强、摩擦因数、活门直径、磨损深度最大容许值、活门锥角、材料硬度等参数对磨损可靠性产生了正向影响，影响度从大到小依次为：压强、摩擦因数、活门直径、磨损深度最大容许值、活门锥角、材料硬度。此外，磨损系数和弹簧预紧力对磨损可靠性产生了负向影响，磨损系数的影响程度大于弹簧预紧力。从分散性来看，活门直径和压强对可靠性的影响程度具有较大的波动性。
本文介绍的磨损深度模型建模方法及可靠性分析方法虽然针对燃油系统的锥形活门，但也可以推广至燃油系统的其他类型活门中，具有一定的通用性。
References
- LIU Shangqin. Investigation of centrifugal pump used as aeroengine main fuel pump[J]. Aeroengine, 2006, 32(2): 43–45 (in Chinese) [Google Scholar]
- FAN Siqi. Aeroengine control[M]. Xi'an: Northwestern Polytechnical University Press, 2008: 24–27 (in Chinese) [Google Scholar]
- HUANG Chaohui. Fuel control system of aeroengine failure and prevention of typical components[M]. Beijing: National Defense Industry Press, 2015 (in Chinese) [Google Scholar]
- CHEN Ming, ZHANG Jingmei. Control system reliability design[M]. Xi'an: Northwestern Polytechnical University Press, 2006 (in Chinese) [Google Scholar]
- WU Weimin, JIANG Hefu. Reliability in aero-engine development[J]. Gas Turbine Experiment and Research, 2004, 17(2): 55–58 (in Chinese) [Google Scholar]
- ZHANG Zhihua. Reliability analysis of engine hydraulic mechanical main fuel regulator[D]. Xi'an: Northwestern Polytechnical University, 2008 (in Chinese) [Google Scholar]
- WANG Jichao. Research on design and simulation of a new type high-reliability main-fuel control unit[J]. Journal of Propulsion Technology, 2015, 36(2): 299–305 (in Chinese) [Google Scholar]
- GAO Han. Modeling and simulation study on the dry friction and wear properties of PEEK[D]. Dalian: Dalian University of Technology, 2021 (in Chinese) [Google Scholar]
- LIU Xiansheng. Research on thermal-mechanical coupled wear behavior of PVD cladding layer for hot-work die steel[D]. Dalian: Dalian University of Technology, 2020 (in Chinese) [Google Scholar]
- DONG Shuna, DU Chunhua, CUl Yahui, et al. Unilateral wear characteristics of brush seal based on Archard model[J]. Journal of Aerospace Power, 2020, 35(7): 1437–1446 (in Chinese) [Google Scholar]
- LI Ling, LI Ganghua, LIN Hong, et al. Fretting wear characteristics of fixed joint surface under thermal and mechanical coupling[J]. Journal of Aerospace Power, 2023, 38(8): 1805–1813 (in Chinese) [Google Scholar]
All Tables
All Figures
|
图1 阀芯轴向剖面结构 |
| In the text | |
|
图2 锥形活门直径对磨损可靠度的影响规律 |
| In the text | |
|
图3 全局灵敏度函数仿真结果 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.