EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 610-619 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 610 - 619
DOI https://doi.org/10.1051/jnwpu/20254330610
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

压电智能材料因具有质量轻、精度高、负载能力强、响应速度快和机械输出效率高等优点而被广泛应用于振动控制[1-2]、形状控制[3-4]、能量俘获[5-6]和结构健康监测[7-8]等领域。在结构振动主动控制应用中，以压电陶瓷材料制成的压电作动器备受关注，尤其是在航空、航天领域，对于执行元件的结构质量、安装空间和负载能力等方面均有较为严苛的限制[9]。因此，在同等体积下, 拥有更高标称推力且负载能力更强的高压压电作动器展现出了巨大的应用潜力[10-11]。然而，压电作动器固有的迟滞特性给它们的应用带来了诸多挑战，如果忽略这一现象，则会严重影响执行元件的跟踪特性，引起控制系统不必要的振荡，甚至造成闭环系统失稳[12]。

研究压电作动器迟滞特性的前提是建立能够准确描述迟滞效应的数学模型，因此研究人员提出了大量迟滞模型来预测压电作动器的迟滞效应，按其建模策略可以分为3类[13]：①基于算子的迟滞模型；②基于非线性微分方程的迟滞模型；③智能模型。其中，基于算子的迟滞模型是由大量基本算子与其对应的权向量相乘后叠加得到的，如经典的Preisach模型[14]、Krasnosel′skii-Pokrovskii模型[15]和Prandtl-Ishlinskii模型[16]等，此类模型可以通过增加基本算子的数目以提升模型的预测精度，但仍存在模型构造复杂、参数辨识计算成本高、逆模型求解困难等问题[16]。基于非线性微分方程的迟滞模型是将迟滞效应看作动态系统的输入/输出关系，例如Bouc-Wen模型[17-19]、Duhem模型[20]、Dahl模型[21]和Jiles-Atherton模型[22]等，相较于迟滞算子模型，这类模型需要辨识的模型参数大幅减少，但其对于压电迟滞特性的描述不够准确，常常在驱动电压极值点附近出现较大的预测误差。Li等[13]在传统Bouc-Wen模型基础上叠加了基于线性函数的蝴蝶型迟滞算子，改善了其在驱动电压极值点附近的模拟精度，但其过高预测了高压区域的迟滞效应。为了解决这一问题，Li等[23]进一步构造了基于指数函数的蝴蝶型迟滞算子，有效改善了高压区域迟滞效应的模拟精度。同时，压电作动器的迟滞特性是不完全对称的，而传统Bouc-Wen模型只能描述关于迟滞环中心点近似对称的迟滞行为，因此，Zhu等[17]通过在传统Bouc-Wen模型中添加非对称项，构造了一种非对称Bouc-Wen模型，迟滞效应预测实验结果表明，非对称Bouc-Wen模型相较于传统Bouc-Wen模型的预测误差降低了约30%。在此基础上，进一步考虑到传统Bouc-Wen模型无法描述与驱动电压频率相关的动态迟滞效应，Zhu等[18]又在非对称Bouc-Wen模型的基础上引入频率因子，提出了一种广义Bouc-Wen模型，并通过压电作动器的位移控制实验，验证了所提建模方法的有效性。此外，还可以采用一种更为通用的方法，即利用静态非线性模块描述静态迟滞效应，同时结合一个动态线性模块，构成Hammerstein模型以在一定频带内实现压电作动器率相关动态迟滞效应的预测[19]。此外，随着人工神经网络技术的迅速发展，智能模型建模策略[24]也逐渐被应用到压电作动器迟滞特性建模研究中，例如，Li等[24]基于BP神经网络的NARMAX模型来预测压电作动器的迟滞效应，通过大量实验数据训练，可以达到很高的预测精度。然而，这类方法往往耗时较长，同时其隐式关系难以直接联系实际物理现象，模型仿真效率不高。

与此同时，如何准确确定迟滞模型所包含的多个未知参数是一个亟需研究的问题。常用的迟滞模型参数辨识算法包括遗传算法[25]、差分进化算法[26]和粒子群算法[27-31]等。其中，粒子群算法具有结构简单、参数较少且易于实现等优点，特别是在求解一些非线性、多峰值的复杂优化问题中，表现出了较强的全局搜索能力，因而在迟滞模型参数辨识领域得到了广泛应用。Ye等[28]在迟滞模型参数辨识中将粒子群算法与遗传算法进行对比研究，验证了粒子群算法可以获得更高质量的辨识结果，且当实验数据被噪声污染时仍然具有良好的优化性能。然而，与传统优化算法相比，粒子群算法存在参数依赖性强、易陷入局部最优、收敛速度慢等缺点。为了更好地平衡算法的全局与局部搜索能力，Shi等[29]在传统粒子群算法的速度更新公式中引入了“惯性权重”这一参数，这种含有惯性权重的粒子群算法后来被称为标准粒子群算法。此后对惯性权重的众多研究成果表明：惯性权重随迭代过程线性递减，将有助于算法优化性能的提高[30]。然而，线性递减惯性权重策略并不能真实反映粒子群算法的非线性搜索过程，限制了其性能发挥[31]。

因此，在上述研究基础上，本文采用非对称Bouc-Wen模型描述静态迟滞效应，进一步结合传递函数模型，构造了高压压电作动器的Hammerstein率相关动态迟滞模型。同时，基于Sigmoid非线性递减惯性权重策略和动态学习因子，提出了一种改进型自适应粒子群算法，并使用高压压电作动器迟滞特性测试实验数据辨识得到了迟滞模型参数。最后，通过高压压电作动器迟滞效应预测实验，验证了所提压电作动器动态迟滞特性建模及参数辨识方法的有效性。

1 压电作动器迟滞特性建模

1.1 静态迟滞模型

Bouc-Wen模型最初是由Bouc在1967年提出的，后经Wen于1976年推广改进，因其具有计算效率高、实时性好、逆模型求解方便等优势而受到广泛关注[23]。经典的Bouc-Wen模型只能描述关于迟滞环中心点近似对称的迟滞行为，而实际压电作动器的迟滞环是不完全对称的，用对称的模型模拟非对称的迟滞环，必然会引起较大的建模误差。因此，本文采用(1)式所示的非对称Bouc-Wen模型[17]。

式中：kp为输入电压的比例系数; h(t)为非线性迟滞算子；k为其比例系数；kh(t)为Bouc-Wen模型的非线性迟滞分量; Δφ为非对称迟滞项, 用于补偿迟滞模型的非对称建模误差; A, β和γ为模型参数, 共同控制迟滞环的大小和形状[12]; λ为非对称补偿系数, 当输入电压升高时\begin{document}$\operatorname{sgn}(\dot{V}(t))=1$\end{document}, 若λ>0, 非对称迟滞项随输入电压的增大, 正向补偿作用越积极, 若λ < 0, 则负向补偿作用越积极; 当输入电压下降时\begin{document}$\operatorname{sgn}(\dot{V}(t))=-1$\end{document}, 非对称迟滞项的作用与电压升高时相反[32]。

1.2 动态迟滞模型

上节所述非对称Bouc-Wen模型仅适用于描述压电作动器的静态迟滞效应, 即迟滞模型的输出不随输入信号频率改变而发生变化。而压电作动器的迟滞效应是率相关的, 不仅与输入信号幅值有关, 还与其频率有关。以风洞模型尾撑结构压电主动减振应用为例[33], 将0.1~25 Hz偏置为500 V的步进正弦扫频信号输入高压压电作动器, 实验测得作动器的输出应变与迟滞环如图 1所示。

thumbnail 图1

高压压电作动器率相关动态迟滞特性测试结果

可以看出, 随着驱动电压频率的增大, 迟滞环的面积逐渐增大, 斜率逐渐降低。因此, 为了实现压电作动器关心频带范围内的率相关动态迟滞效应预测, 本文基于非对称Bouc-Wen模型, 进一步结合传递函数模型, 建立压电作动器的Hammerstein率相关动态迟滞模型。

Hammerstein模型是一种模块连接的非线性模型, 通常由一个静态非线性模块与一个动态线性模块串联构成, 其结构简单, 但可以方便地描述一大类非线性过程, 包括压电作动器的迟滞非线性[19]。因此, 采用非对称Bouc-Wen模型与传递函数模型分别作为Hammerstein模型的静态非线性部分和动态线性部分, 使其能够预测给定频带内的压电作动器率相关动态迟滞效应, 模型框图如图 2所示。用kH(V)代表(1)式的非线性分量, 可以得到Hammerstein率相关动态迟滞模型的应变输出为

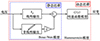thumbnail 图2

Hammerstein率相关动态迟滞模型框图

2 改进型自适应粒子群算法

粒子群算法最早是由Eberhart等于1995年提出的, 具有算法简单、控制参数少、易于实现等优点[34]。粒子群算法将每个优化问题的解视为搜索空间中的一只鸟, 每只鸟被抽象成一个没有质量和体积的“粒子”, 每个粒子具有2个基本属性: 速度和位置, 分别由(3)~(4)式确定。粒子的位置表征优化问题的可行解, 粒子的速度决定它们飞行的方向和距离, 粒子的优劣由优化函数的适应度值评价。

式中：vi(t)代表第i个粒子的速度；xi(t)为粒子的位置；cp和cg分别为个体学习因子和社会学习因子; r1和r2为均匀分布于[0, 1]之间的随机数, 且相互独立, 用于增加粒子飞行的随机性; pi(t)和g(t)分别表示迄今为止第i个粒子搜索到的个体最优位置和整个粒子群搜索到的全局最优位置, 分别称为个体极值与最优极值。(3)式右边的三部分分别代表“惯性”环节、“认知学习”环节和“社会学习”环节, 3个环节共同决定粒子的更新方向与距离。

为了进一步提升粒子群算法的优化性能, Shi和Eberhart在传统粒子群算法的更新公式(3)中引入了“惯性权重w”这一参数，将其修改为[29]

惯性权重w决定了粒子前一步速度对当前速度的影响程度, 起到了平衡算法全局搜索能力与局部搜索能力的作用。由(4)~(5)式组成的粒子群算法也被称为标准粒子群(particle swarm optimization, PSO)算法。随后, Shi等[30]进一步提出了线性递减惯性权重策略, 即在算法迭代初期, 使用大的惯性权重, 使算法具有更强的全局搜索能力; 随后线性递减惯性权重, 在算法迭代后期使用较小的惯性权重以提升局部搜索能力。线性递减惯性权重的更新公式为

式中: wstart为初始惯性权重; wend为最终惯性权重; t表示当前迭代次数; Tmax为允许的最大迭代次数。

经大量实验计算, Shi等[30]发现对于大多测试函数, 线性递减惯性权重粒子群(linear decreasing inertial weight PSO, LDIW-PSO)算法相较于标准粒子群算法的收敛速度更快且求解精度更高。然而, 线性递减惯性权重策略并不能真实反映粒子群算法的非线性搜索过程, 因此, 本文在上述研究基础上, 针对高压压电作动器迟滞模型参数的辨识需求, 提出了一种基于Sigmoid函数的非线性递减惯性权重策略, 如(7)式所示。

式中，K, d和p为控制参数, 如图 3a)所示, K用于控制惯性权重曲线在下降阶段的变化率, K越大, 下降阶段的变化率就越大; d用于控制惯性权重曲线的下降时机, d越小, 惯性权重越早下降至最终惯性权重附近, 如图 3b)所示, K和d可根据用户的实际优化需求自主调整。p则控制着初始惯性权重值, 如图 3c)所示。基于Sigmoid函数的非线性递减惯性权重策略在迭代初期w的取值较大且变化较慢, 有利于算法进行全局搜索; 后期w的取值小且变化慢, 有利于算法快速收敛, 从而有效提升了粒子群算法的整体性能。

thumbnail 图3

非线性递减惯性权重策略参数分析结果

此外, 在标准粒子群算法中, 学习因子cp和cg一般取为定值, 为进一步改善算法的收敛特性, 动态调整个体信息和社会信息利用程度, 本文又发展了一种动态调节学习因子策略。学习因子更新公式为

式中, cmax和cmin分别为学习因子的最大值与最小值。由学习因子更新公式可知, 在算法迭代初期, 较大的个体认知有利于寻找个体极值, 提升算法的全局搜索能力; 迭代后期, 以社会认知为主有利于粒子群趋向于最优极值, 加快算法收敛速度。以cmax=2.5, cmin=1.5和Tmax=100为例, 动态学习因子的迭代曲线如图 4所示。

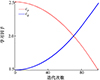thumbnail 图4

动态学习因子迭代曲线

综上, 本文所提改进型自适应粒子群(modified adaptive PSO, MA-PSO)算法流程如下。

步骤1  初始化粒子群算法, 随机更新粒子的位置与速度, 设置种群数量与最大迭代次数;

步骤2  计算每个粒子对于优化函数的适应度值, 确定个体极值pi(t)和最优极值g(t);

步骤3  根据(4)~(5)式更新每个粒子的速度与位置;

步骤4  迭代次数t加1, 根据(7)~(9)式更新惯性权重w、个体学习因子cp和社会学习因子cg;

步骤5  若t≤Tmax, 返回步骤2;若t>Tmax, g(t)为所得最优解。

3 高压压电作动器迟滞效应预测实验

为了验证本文所提Hammerstein率相关动态迟滞模型和改进型自适应粒子群算法的高效性, 本节开展高压压电作动器迟滞特性测试、迟滞模型参数辨识与模型验证研究。

3.1 实验系统

以PI/P-016.20型高压压电作动器为研究对象, 开展迟滞特性测试实验。具体实验流程为: 通过Matlab/Simulink在dSPACE实时控制仿真系统中搭建信号发生器模块产生驱动电压信号, 通过输出板卡传递至压电功放, 经放大后驱动高压压电作动器。同时, 在作动器表面粘贴应变片, 由动态应变放大器驱动，测量压电作动器的轴向输出应变, 随后通过dSPACE采集板卡输入至主机, 采样频率设置为1 000 Hz。所用实验设备信息详情见表 1，实验现场如图 5所示。

thumbnail 图5

高压压电作动器迟滞特性测试实验布置

表1

实验设备信息

3.2 迟滞模型参数辨识与模型验证

Hammerstein率相关动态迟滞模型参数辨识可分两步进行。

在准静态条件下, 将5 Hz以内的驱动电压输入压电作动器时, 作动器的迟滞环几乎没有变化[23]。因此, 首先采用峰-峰值分别为100~900 V, 200~800 V和300~700 V, 频率为5 Hz的正弦信号驱动高压压电作动器进行静态迟滞模型辨识, 基于所提改进型自适应粒子群算法, 结合压电作动器迟滞特性测试实验数据, 辨识非对称Bouc-Wen模型参数。定义性能指标为[13]

式中：ER代表迟滞模型预测输出应变与压电作动器实际输出应变的相对误差; i=1, 2, 3分别代表 3组不同峰-峰值驱动电压下的迟滞特性测试实验数据; ymi和yei分别为迟滞模型预测输出应变的时间序列和由dSPACE采集得到的压电作动器实际应变输出的时间序列; max(yei)为对应工况下, 压电作动器满量程输出应变的最大值。

本节采用PSO算法、LDIW-PSO算法和所提MA-PSO算法分别辨识非对称Bouc-Wen模型参数, 对比验证MA-PSO算法的优越性。3种粒子群算法的参数设置如表 2所示, 为了更好地进行对比研究, MA-PSO算法取p=2, 即初始惯性权重约为0.9, 与线性递减惯性权重策略的初始惯性权重保持一致。每种算法进行3次迟滞模型参数辨识实验, 分别取其最优值作为其辨识结果, 3种粒子群算法的优化结果如图 6所示。

thumbnail 图6

粒子群算法优化结果

从图 6可知, 本文所提MA-PSO算法在迭代初期收敛速度慢, 算法趋向于全局搜索, 在迭代后期, 收敛速度快且迅速逼近全局最优极值, 同时可以通过调节控制参数适应不同的优化需求, 例如, 本节取d=0.2, 则算法在最大迭代次数的20%处, 即第20代时, 惯性权重迅速降低, 算法由全局搜索主导迅速转化为局部搜索主导, 从而有效提升了算法的收敛速度。而PSO算法则出现了早熟现象, 提前收敛于局部最优值。LDIW-PSO算法虽然同样采用了迭代初期大惯性权重, 迭代后期小惯性权重的策略, 但其线性递减方案无法真实反映粒子群算法的非线性优化过程, 导致迭代后期算法的收敛速度较慢, 最终优化结果不佳。

以驱动电压峰-峰值200~800 V为例(其余结果类似), 不同优化算法下, 非对称Bouc-Wen模型的预测结果如图 7所示。由图 7可知, 基于所提MA-PSO算法辨识得到非对称Bouc-Wen模型具有很好的静态迟滞效应预测精度, 相较于PSO算法, 驱动电压极值点附近的预测误差明显降低, 并且可以有效捕捉压电作动器的初始加载回路, 最终预测误差仅为2.65%。辨识得到的使相对误差ER最小化的迟滞模型参数见表 3。

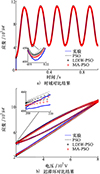thumbnail 图7

非对称Bouc-Wen模型预测结果

与此同时, 在现有的迟滞特性建模研究中, 主-次迟滞环切换现象是一个重要的迟滞特征[13]。其中, 大幅值输入信号形成的迟滞环称为主迟滞环, 在主迟滞环内部由于输入信号幅值减小而形成的迟滞环称为次迟滞环。在结构振动主动控制应用中, 主-次迟滞环之间是否能够平稳过渡, 是评价迟滞模型的一个重要参考标准。为了验证非对称Bouc-Wen模型对于主-次迟滞环切换现象的跟踪性能, 以频率为5 Hz, 峰-峰值由100~900 V切换至300~700 V的正弦信号作为驱动电压, 得到的迟滞效应预测结果如图 8所示。

thumbnail 图8

主-次迟滞环切换现象模拟结果

由图 8可知, 当驱动电压的幅值发生突变时, 非对称Bouc-Wen模型依然可以保持良好的跟踪性能, 从而实现压电作动器主-次迟滞环切换现象的模拟。

当非对称Bouc-Wen模型参数确定后, 为了实现关心频带内的率相关动态迟滞特性建模, 利用如图 1a)所示的峰-峰值为100~900 V, 频率范围为0.1~25 Hz的步进正弦扫频信号驱动高压压电作动器进行Hammerstein模型辨识。具体流程为: 首先忽略串联的传递函数模型, 基于辨识得到的非对称Bouc-Wen模型, 输入正弦扫频信号得到中间变量

随后以中间变量yi为输入, 压电作动器正弦扫频实验测量得到的应变为输出, 使用Matlab/System Identification工具箱辨识得到二阶传递函数模型

将其与非对称Bouc-Wen模型串联，即可得到高压压电作动器的Hammerstein率相关动态迟滞模型。

最后，验证Hammerstein模型在不同频率(5, 10, 20 Hz)和峰-峰值(100~900, 200~800, 300~700 V)驱动电压下的迟滞效应预测效果。实验结果如图 9所示，可以看到，本文所建立的Hammerstein率相关动态迟滞模型不仅能够预测不同峰-峰值驱动电压下的迟滞效应，并且对于关心频带内不同频率驱动电压下的作动器应变输出具有令人满意的预测效果，各驱动电压频率下的迟滞效应预测误差分别为2.35%, 2.45%和3.79%。

thumbnail 图9

不同峰-峰值、频率驱动电压下的迟滞效应预测结果

此外，为了进一步验证Hammerstein模型对于不同频率主-次迟滞环切换现象的跟踪效果，分别采用频率为10 Hz和20 Hz，峰-峰值由100~900 V切换至300~700 V的正弦信号作为驱动电压，预测结果如图 10~11所示。从图 10~11中可以看出，对于不同频率的驱动电压，所建立的Hammerstein率相关动态迟滞模型均能很好地模拟压电作动器主-次迟滞环的切换现象，同时能够捕获压电作动器的初始加载回路，实现了高压压电作动器的高精度动态迟滞特性建模。

thumbnail 图10

10 Hz驱动电压下的主-次迟滞环切换现象模拟结果

thumbnail 图11

20 Hz驱动电压下的主-次迟滞环切换现象模拟结果

表2

粒子群算法参数设置

表3

非对称Bouc-Wen模型参数辨识结果

4 结论

针对高压压电作动器迟滞特性建模及参数辨识问题，提出了一种基于Hammerstein模型和MA-PSO算法的压电作动器动态迟滞特性建模及参数辨识方法。首先，通过结合非对称Bouc-Wen模型和传递函数模型，建立了高压压电作动器的Hammerstein率相关动态迟滞模型。其次，基于Sigmoid非线性递减惯性权重策略和动态学习因子，提出了一种MA-PSO算法，并使用高压压电作动器迟滞特性测试实验数据辨识得到了迟滞模型参数，静态迟滞效应的预测误差仅为2.65%，验证了所提算法在收敛速度和优化效果方面的优越性。最后，通过高压压电作动器迟滞效应预测实验，验证了所建立的Hammerstein模型可以高效描述其动态迟滞效应，平均预测误差小于3%，并且在关心频带内对于作动器驱动电压频率和幅值的改变具有很强的适应性。

与此同时，基于本文所建立的Hammerstein模型，可以很方便地构造其逆模型实现压电作动器迟滞非线性的高精度动态补偿，从而能够有效降低压电主动控制系统的设计难度，提升控制系统的稳定性和能源利用效率。此外，本文所提MA-PSO算法同样可以应用于其他非线性、多峰值的复杂优化问题，并且能够通过调节控制参数快速适应不同的优化需求。

References

  1. JUNGBLUT J, HAAS J, RINDERKNECHT S. Active vibration control of an elastic rotor by using its deformation as controlled variable[J]. Mechanical Systems and Signal Processing, 2022, 165: 108371 [Google Scholar]
  2. LI W, YANG Z, LI K, et al. Hybrid feedback PID-FxLMS algorithm for active vibration control of cantilever beam with piezoelectric stack actuator[J]. Journal of Sound and Vibration, 2021, 509: 116243 [Google Scholar]
  3. SONG X, TAN S, WANG E, et al. Active shape control of an antenna reflector using piezoelectric actuators[J]. Journal of Intelligent Material Systems and Structures, 2019, 30(18/19): 2733–2747 [Google Scholar]
  4. YANG S Y, NGOI B. Shape control of beams by piezoelectric actuators[J]. AIAA Journal, 2000, 38(12): 2292–2298 [Google Scholar]
  5. SEZER N, KOC M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting[J]. Nano Energy, 2021, 80: 105567 [CrossRef] [Google Scholar]
  6. CHEN Y, YANG Z, CHEN Z, et al. Design, modeling, and experiment of a multi-bifurcated cantilever piezoelectric energy harvester[J]. Journal of Intelligent Material Systems and Structures, 2021, 32(20): 2403–2419 [Google Scholar]
  7. QING X, LI W, WANG Y, et al. Piezoelectric transducer-based structural health monitoring for aircraft applications[J]. Sensors, 2019, 19(3): 545 [Google Scholar]
  8. DRAGASIUS E, EIDUKYNAS D, JURENAS V, et al. Piezoelectric transducer-based diagnostic system for composite structure health monitoring[J]. Sensors, 2021, 21(1): 253 [Google Scholar]
  9. LIU W, ZHOU M, WEN Z, et al. An active damping vibration control system for wind tunnel models[J]. Chinese Journal of Aeronautics, 2019, 32(9): 2109–2120 [Google Scholar]
  10. SHEN X, DAI Y, CHEN M, et al. Active vibration control of the sting used in wind tunnel: comparison of three control algorithms[J]. Shock and Vibration, 2018, 2018: 1905049 [Google Scholar]
  11. ZHANG L, DAI Y, SHEN X, et al. Research on an active pitching damper for transonic wind tunnel tests[J]. Aerospace Science and Technology, 2019, 94: 105364 [Google Scholar]
  12. HASSANI V, TJAHJOWIDODO T, THANH NHO D. A survey on hysteresis modeling, identification and control[J]. Mechani-cal Systems and Signal Processing, 2014, 49(1/2): 209–233 [Google Scholar]
  13. LI K, YANG Z, LALLART M, et al. Hybrid hysteresis modeling and inverse model compensation of piezoelectric actuators[J]. Smart Materials and Structures, 2019, 28(11): 115038 [Google Scholar]
  14. LUO Y, QU Y, ZHANG Y, et al. Hysteretic modeling and simulation of a bilateral piezoelectric stack actuator based on preisach model[J]. International Journal of Applied Electromagnetics and Mechanics, 2019, 59(1): 271–280 [Google Scholar]
  15. XU R, TIAN D, WANG Z. Adaptive tracking control for the piezoelectric actuated stage using the Krasnosel' skii-Pokrovskii operator[J]. Micromachines, 2020, 11(5): 537 [Google Scholar]
  16. TAN U X, LATT W T, SHEE C Y, et al. Feedforward controller of ill-conditioned hysteresis using singularity-free Prandtl-Ishlinskii model[J]. IEEE-ASME Trans on Mechatronics, 2009, 14(5): 598–605 [Google Scholar]
  17. ZHU W, WANG D H. Non-symmetrical Bouc-Wen model for piezoelectric ceramic actuators[J]. Sensors and Actuators A: Physical, 2012, 181: 51–60 [Google Scholar]
  18. ZHU W, RUI X T. Hysteresis modeling and displacement control of piezoelectric actuators with the frequency-dependent behavior using a generalized Bouc-Wen model[J]. Journal of the International Societies for Precision Engineering and Nanotechnology, 2016, 43: 299–307 [Google Scholar]
  19. WANG Z, ZHANG Z, MAO J, et al. A hammerstein-based model for rate-dependent hysteresis in piezoelectric actuator[C]//24th Chinese Control and Decision Conference, Taiyuan, 2012 [Google Scholar]
  20. WANG G, CHEN G. Identification of piezoelectric hysteresis by a novel Duhem model based neural network[J]. Sensors and Actuators A: Physical, 2017, 264: 282–288 [Google Scholar]
  21. AHMAD I, ALI M A, KO W. Robust mu-synthesis with Dahl model based feedforward compensator design for piezo-actuated micropositioning stage[J]. IEEE Access, 2020, 8: 141799–141813 [Google Scholar]
  22. YANG Y, YANG B, NIU M. Parameter identification of Jiles-Atherton model for magnetostrictive actuator using hybrid niching coral reefs optimization algorithm[J]. Sensors and Actuators A: Physical, 2017, 261: 184–195 [Google Scholar]
  23. LI W, LIU K, YANG Z, et al. Dynamic modeling and disturbance rejection compensation for hysteresis nonlinearity of high voltage piezoelectric stack actuators[J]. Smart Materials and Structures, 2023, 32(2): 025007 [Google Scholar]
  24. LI W, CHEN X. Compensation of hysteresis in piezoelectric actuators without dynamics modeling[J]. Sensors and Actuators A: Physical, 2013, 199: 89–97 [Google Scholar]
  25. ZHOU Y, HU J, HUANG Y, et al. Parameter identification and hysteresis compensation for piezoelectric stack based on Bouc-Wen model using genetic algorithm[C]//38th Chinese Control Conference, Guangzhou, 2019 [Google Scholar]
  26. CHEN G, YAN X, CAI J, et al. Hysteresis nonlinear modeling and compensation of piezoelectric ceramic sensors in micro measurement systems[J]. Measurement Science and Technology, 2018, 29(9): 095102 [Google Scholar]
  27. LI Y, XU Q. Adaptive sliding mode control with perturbation estimation and PID sliding surface for motion tracking of a piezo-driven micromanipulator[J]. IEEE Trans on Control Systems Technology, 2010, 18(4): 798–810 [Google Scholar]
  28. YE M, WANG X. Parameter estimation of the Bouc-Wen hysteresis model using particle swarm optimization[J]. Smart Materials and Structures, 2007, 16(6): 2341–2349 [Google Scholar]
  29. SHI Y, EBERHART R. A modified particle swarm optimizer[C]//1998 IEEE International Conference on Evolutionary Computation, 1998 [Google Scholar]
  30. SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation, 1999 [Google Scholar]
  31. YUHUI S, EBERHART R C. Fuzzy adaptive particle swarm optimization[C]//Proceedings of the 2001 Congress on Evolutionary Computation, 2001 [Google Scholar]
  32. QIN H, BU N, CHEN W, et al. An asymmetric hysteresis model and parameter identification method for piezoelectric actuator[J]. Mathematical Problems in Engineering, 2014(2014): 932974 [Google Scholar]
  33. LI W, YANG Z, ZHU X, et al. Piezoelectric adaptive active vibration suppression for wind-tunnel model support sting[J]. Smart Materials and Structures, 2024, 33(8): 085020 [Google Scholar]
  34. EBERHART R C, SHI Y H. Particle swarm optimization: developments, applications and resources[C]//Congress on Evolutionary Computation, Seoul, 2001 [Google Scholar]

All Tables

表1

实验设备信息

In the text
表2

粒子群算法参数设置

In the text
表3

非对称Bouc-Wen模型参数辨识结果

In the text

All Figures

thumbnail 图1

高压压电作动器率相关动态迟滞特性测试结果
In the text
thumbnail 图2

Hammerstein率相关动态迟滞模型框图
In the text
thumbnail 图3

非线性递减惯性权重策略参数分析结果
In the text
thumbnail 图4

动态学习因子迭代曲线
In the text
thumbnail 图5

高压压电作动器迟滞特性测试实验布置
In the text
thumbnail 图6

粒子群算法优化结果
In the text
thumbnail 图7

非对称Bouc-Wen模型预测结果
In the text
thumbnail 图8

主-次迟滞环切换现象模拟结果
In the text
thumbnail 图9

不同峰-峰值、频率驱动电压下的迟滞效应预测结果
In the text
thumbnail 图10

10 Hz驱动电压下的主-次迟滞环切换现象模拟结果
In the text
thumbnail 图11

20 Hz驱动电压下的主-次迟滞环切换现象模拟结果
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.