| Issue |
JNWPU
Volume 37, Number 5, October 2019
|
|
|---|---|---|
| Page(s) | 897 - 902 | |
| DOI | https://doi.org/10.1051/jnwpu/20193750897 | |
| Published online | 14 January 2020 | |
K-Terminal Network Permutation Importance Measure Based on Mixture C-Spectrum
基于混合C-谱的K-终端网络置换重要度计算方法
1
School of Science, Lanzhou University of Technology, Lanzhou 730050, China
2
School of Mechatronics, Northwestern Polytechnical University, Xi'an 710072, China
Received:
22
October
2018
The construction spectrum(C-spectrum) is often used to exploit the network reliability and importance measure. It depends only on the network structure and hence called structure invariant. Importance measure can be used to quantify the criticality of edge within a network. This paper aim at generalizing the traditional permutation importance measure to accommodate the case of K-terminal network in which all the edges fail with independent and equal probability. A concept for mixture C-spectrum is introduced to evaluate the permutation importance measure of edges. It is proved that the rankings according to the permutation importance measure depend only on the network structure through the mixture C-spectrum when the network has special structure or the reliability of edge is sufficient large. Finally, numerical experiment show that the Monte Carlo algorithm based on the mixture C-spectrum can be efficiently used to evaluate the permutation importance measure.
摘要
重要度可以量化网络边对整个网络可靠性(故障)的影响程度,而C-谱是研究网络可靠性及重要度的一个有力工具。假设网络中每条边具有相同的可靠性,将二态关联系统中的传统置换重要度推广到K-终端网络,设计了基于混合C-谱的蒙特卡罗算法来评估该重要度。理论分析表明:当网络具有某种特殊结构或者边的可靠性足够大时,网络边的置换重要度排序仅依赖于网络结构,而与边的可靠性无关。最后,结合算例演示了如何利用传统置换重要度评估K-终端网络中网络边的重要程度。
Key words: K-terminal network / permutation importance measure / mixture C-spectrum / Monte Carlo
关键字 : K-终端网络 / 置换重要度 / 混合C-谱 / 蒙特卡罗
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
由于网络在社会生活中扮演了重要的角色, 所以网络可靠性和重要度吸引了许多学者的关注。网络一般由节点和边组成, 其中节点表示道路交叉口、控制中心等, 而边表示通讯电缆、道路等。在K-终端网络中, 一部分节点称为终端, 网络运行当且仅当所有终端被一些运行的边连通。假设节点绝对可靠, 而边以某种概率发生故障, 边故障可能导致整个网络处于故障状态。因此K-终端网络可靠性被定义为网络中所有终端彼此连通的概率[1]。
网络可靠性分析的目的是识别网络瓶颈和量化网络边的故障(运行)对整个网络的影响程度。作为一种可靠性分析工具, 重要度提供了数值指标, 能够量化不同的边对网络可靠性(故障)的影响程度, 从而对网络的边进行排序。在二态关联系统领域, 常见的重要度包括Birnbaum-重要度[2-2]、FV-重要度[4-4]、贝叶斯-重要度[6]、集成重要度[7-7]、置换重要度[9-9]。在网络领域, Page和Perry[11]引进了可靠性多项式去量化网络边的相对重要性。对于一类可约网络, Hsu等人[12]设计了一种“两阶段”算法评估网络边的重要度。该算法第一阶段执行网络化简; 第二阶段跟踪化简步骤和评估边的重要度。Hong等人[13]提出了2条边的联合重要度。该联合重要度考虑了2条边的互动对整个网络可靠性的影响。
对于中等或大型网络, 网络重要度的理论分析和精确计算之间存在着巨大的鸿沟[1]。因此, 一般采用数值近似的方法评估网络边的重要度。当网络中的每条边有相同的可靠性时, Gertsbak等人[14-14]将传统的FV-重要度、Birnbaum-重要度、以及联合重要度推广到K-终端网络, 设计了基于网络谱的蒙特卡罗方法评估这些重要度。网络谱分为D-谱和C-谱, 分别与网络的割集和路集紧密相关。由于它们的值都仅依赖于网络结构, 故称为结构不变量。本文将传统的置换重要度推广到K-终端网络。在二态关联系统背景下, 传统的置换重要度通过枚举所有割集或者路集的方法评估了系统组件的重要度。然而, 由于K-终端网络结构的复杂性, 本文提出了2条边的混合C-谱的概念, 并设计了基于混合C-谱的蒙特卡罗算法评估网络边的置换重要度。研究结果表明, 当网络拥有一定的特殊结构, 或者网络边的可靠性足够大时, 基于置换重要度的网络边的排序仅依赖于网络结构, 与边的可靠性无关。
1 基本概念和定义
本文研究K-终端网络(简称网络), 该网络是一个由节点和边构成的无向图N=(V, E, K)。V是网络中节点的集合, E是网络边的集合且|E|=n, K(K⊆V)是由一些特殊节点构成的集合, 称为网络终端集合。针对由二态边组成的二态网络, 令二态变量xi=1(0)表示边i处于运行(故障)状态。边i的可靠性为pi, 即pi=P(xi=1)。结构函数φ(x)确定网络状态, 这里x=(x1, x2, …, xn)。φ(x)=1(0)表示网络处于运行(故障)状态。网络运行当且仅当所有终端被一条路连通。路为若干运行边的集合, 其连通网络所有终端。网络可靠性定义为该网络处于运行状态的概率, 即R=P(φ(x)=1)=R(p1, p2, …, pn)。
假设网络所有边的故障相互独立且有相同可靠性。在此背景下, 网络可靠性和重要度可利用基于C-谱的方法去评估。C-谱的定义如下[1]:
假设网络所有边处于故障状态, 令π=(i1, i2, …, in)为网络边集E的一个随机置换。沿着该置换π, 从左到右依次“复活”各个边。当边ij“复活”时(即该构造过程的第j步), 令fj为网络“复活”的概率。离散概率向量f=(f1, f2, …, fn)称为网络的C-谱。网络累积C-谱定义为:F(k)=f1+f2+…+fk, 这里k=1, 2, …, n。令B(k)为恰包含k条边的路的数目, 则下列公式成立[1]:
由此, 当随机的恰有k条边运行时, F(k)可解释为网络处于运行状态的概率。注意这里的C-谱仅依赖于给定网络的结构, 故称为结构不变量。固定边i, 恰含有k条边的所有路可分为2类:一类包含边i, 一类不包含边i。因而B(k)可拆成两部分, 如下
式中,B(k, 1i)(B(k, 0i))表示恰含有k条运行边的路的数目, 其中边i运行(故障)。公式(2)代入公式(1)后, F(k)亦可拆成两部分, 如下
式中
由公式(4)~(5), 当随机恰有k条边运行时, F(k, 1i)(F(k, 0i))可解释为网络处于运行状态, 且边i运行(故障)的概率。称F(k, 1i), F(k, 0i)为网络边i的C-谱[1]。
进一步, 记B(k, 1i, 0j)(B(k, 0i, 1j))表示恰含有k条边的路的数目, 其中边i运行(故障), 边j故障(运行)。相似于公式(4)~(5), 令
根据公式(6)和(7), 当随机恰有k条边运行时, F(k, 1i, 0j)(F(k, 0i, 1j))可解释为网络处于运行状态, 且边i运行(故障), 边j故障(运行)的概率。称F(k, 1i, 0j), F(k, 0i, 1j)为网络边i, j的混合C-谱。
在网络N中, 对于给定的一条边j, 删除边j得到子网络N-j; 收缩边j为一个新节点, 得到子网络N*j。若收缩的边j邻接的节点有网络N的终端, 则边j收缩后的新节点为子网络N*j的终端。FN(k), FN-j(k), FN*j(k)分别表示网络N, 子网络N-j, 子网络N*j的累积C-谱。以此类推, 网络N、子网络N-j、以及子网络N*j的边的C-谱和两条边混合C-谱可类似表示。
下面的定理揭示了网络边的混合C-谱, 边的C-谱, 以及网络累积C-谱之间的关系。
定理1 给定一个由n条边组成的网络N, 下面的结论成立
式中,k=1, 2, …, n-1;i=1, 2, …, j-1, j+1, …, n。
证明 在网络N中, 若已知边j运行, 则收缩边j, 由路的定义, 得下面公式
式中,k=1, 2, …, n-1;i=1, 2, …, j-1, j+1, …, n。
在网络N中, 恰含有k+1条边且包含边j的所有路可分为2类:一类包含边i, 一类不包含边i。故下列公式成立
公式(10)和(11)代入(12)式, 得到下面公式
根据C-谱的定义(即公式(7), (1), (4)), 公式(13)可等价写为
从公式(14)解出FN(k+1, 1j, 0i)后, 得到公式(8)。
另外, 当边j故障, 则从网络N中删除边j后, 由路的定义, 下列公式成立
根据C-谱的定义(即公式(4), (6)), 公式(15)可以等价的写为
从公式(16)解出FN(k, 0j, 1i), 可得公式(9)。从而定理得证。
注意 当网络N只含有2个终端时, 如果边j本身为一条路时({j}称为网络N的单边路), 则BN(1, 1j, 0i)=1;否则BN(1, 1j, 0i)=0。从而根据混合C-谱的定义(见公式(7)), 有下列公式成立
2 基于混合C-谱的置换重要度
在解决关联系统的冗余分配问题时, Boland等人[10]提出了置换重要度。对于关联系统的任意2个组件i和j, 如果R(1i, 0j, p)>R(0i, 1j, p), 则称组件i比组件j更重要, 记为i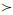 j, 其中R(1i, 0j, p)=P(φ(x)=1|xi=1, xj=0), R(0i, 1j, p)=P(φ(x)=1|xi=0, xj=1)。
j, 其中R(1i, 0j, p)=P(φ(x)=1|xi=1, xj=0), R(0i, 1j, p)=P(φ(x)=1|xi=0, xj=1)。
给定一个由n条边构成的K-终端网络, 假设所有边有共同的可靠性p(q=1-p)。对于该网络任意的2条边i和j, 根据全概率公式, 得下面公式
公式(6)代入公式(18)后, 得下面公式
同理, 由全概率公式, 下列公式成立
公式(7)代入公式(20)后, 得下面公式
比较公式(19)和(21), 得下面定理。
定理2 给定一个由n条边组成的K-终端网络。对于该网络任意的2条边i和j, 下面的结论成立:
1) 若F(k, 1i, 0j)≥F(k, 0i, 1j)(F(k, 1i, 0j)≤F(k, 0i, 1j))对一切k=1, 2, …, n-2成立, 且对某个k, 不等式严格成立, 则i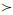 j(i
j(i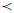 j)对一切p∈(0, 1)成立。
j)对一切p∈(0, 1)成立。
2) 令m=max{k|F(k, 1i, 0j)≠F(k, 0i, 1j)}。若F(m, 1i, 0j)>F(m, 0i, 1j), 则对于充分大的p, i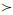 j成立。
j成立。
证明
1) 由置换重要度定义, i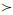 j当且仅当R(1i, 0j, p)>R(0i, 1j, p), 即R(1i, 0j, p)-R(0i, 1j, p)>0。将公式(19)与公式(21)作差相减后, 只须证明下列不等式成立
j当且仅当R(1i, 0j, p)>R(0i, 1j, p), 即R(1i, 0j, p)-R(0i, 1j, p)>0。将公式(19)与公式(21)作差相减后, 只须证明下列不等式成立
由于F(k, 1i, 0j)≥F(k, 0i, 1j)对一切k=1, 2, …, n-2成立, 故公式(22)对一切p∈(0, 1)成立。从而得证。
2) 根据m的定义和公式(22), i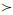 j当且仅当下列不等式成立
j当且仅当下列不等式成立
注意当p→1(即q→0)时, 单项式(F(k, 1i, 0j)-F(k, 0i, 1j))pkqn-k-2→0。(n-k-2)越大(即k越小), 该单项式趋向于0越快。故由m定义, 当q→0时, 公式(23)成立当且仅当单项式(F(m, 1i, 0j)-F(m, 0i, 1j))pmqn-m-2>0(忽略高阶无穷小)。结合已知条件F(m, 1i, 0j)>F(m, 0i, 1j), 故对于充分大的p, i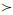 j成立。从而定理得证。
j成立。从而定理得证。
注意 根据置换重要度的定义, 对于网络中任意2条边i和j, i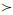 j依赖于网络的结构和网络边的可靠性p。定理2说明, 当网络拥有特殊的结构, 即F(k, 1i, 0j)≥F(k, 0i, 1j)对一切k=1, 2, …, n-2成立, 则网络边的置换重要度排序与边的可靠性无关; 另外, 当网络边的可靠性足够大时, 网络边的置换重要度排序亦仅依赖于网络结构。
j依赖于网络的结构和网络边的可靠性p。定理2说明, 当网络拥有特殊的结构, 即F(k, 1i, 0j)≥F(k, 0i, 1j)对一切k=1, 2, …, n-2成立, 则网络边的置换重要度排序与边的可靠性无关; 另外, 当网络边的可靠性足够大时, 网络边的置换重要度排序亦仅依赖于网络结构。
3 算例分析
这里通过一个算例演示如何利用传统置换重要度评估K-终端网络边的重要程度。给定立方体网络H3, 节点1, 3, 6为终端节点, 如图 1所示。基于置换重要度, 本节对该网络所有边的重要性进行排序。网络的累积C-谱以及边的C-谱的数值估计借助Gertsbakh等人[1]设计的蒙特卡罗方法。然后, 根据公式(8)~(9), 得到2条边的混合C-谱。表 1(表 2)提供了网络H3边3, i的混合C-谱F(k, 03, 1i)(F(k, 13, 0i)), i=1, 2, 4, 5, …, 12, F(k, 03, 1i) (F(k, 13, 0i))缩写为03, 1i(13, 0i)。
根据定理2, 为了比较2条边的置换重要度, 只须比较它们相应的混合C-谱。由表 1, 表 2得知, F(k, 13, 08)≥F(k, 03, 18), 且F(k, 13, 01)≤F(k, 03, 11)对于所有的k=1, 2, …, 11成立。故1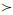 3
3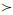 8对于所有的p∈(0, 1)成立。同理, 分析H3网络12条边所有混合C-谱, 发现这些边可分为3组, 每组有相同的重要性。第一组为{1, 4, 5}, 第二组为{2, 3, 6, 7, 9, 11}, 第三组为{8, 10, 12}。基于置换重要度, 第一组最重要, 其余类推。
8对于所有的p∈(0, 1)成立。同理, 分析H3网络12条边所有混合C-谱, 发现这些边可分为3组, 每组有相同的重要性。第一组为{1, 4, 5}, 第二组为{2, 3, 6, 7, 9, 11}, 第三组为{8, 10, 12}。基于置换重要度, 第一组最重要, 其余类推。
对于其他任意网络结构, 亦可采用同样方法求得其混合C-谱。从而根据定理2的结论对网络边进行排序。
事实上, 第一组边{1, 4, 5}有一个共同的特性:与这些边邻接的一个节点为终端, 而相邻的另外一个节点距离其他2个终端的距离都为1。第二组边{2, 3, 6, 7, 9, 11}的共同特性:与这些边邻接的一个节点为终端, 而相邻的另外一个节点距离其他某一个终端的距离为1。其余为第三组边{8, 10, 12}。
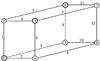 |
图 1 立方体网络H3, K={1, 3, 6} |
边3, i的混合C-谱F(k, 03, 1i)
边3, i的混合C-谱F(k, 13, 0i)
4 结论
本文将二态关联系统的置换重要度推广到K-终端网络。假设每条边的可靠性相同, 本文提出混合C-谱的概念, 给出K-终端网络的边的置换重要度的计算方法。理论分析认为, 当网络具有某种特殊结构或者边的可靠性足够大时, 网络边的置换重要度排序仅依赖于网络结构。数值计算结果表明, 基于混合C-谱的计算方法能有效评估网络边的置换重要度。本文结果有助于进一步理解K-终端网络, 并为网络可靠性优化提供了基础。
References
- Gertsbakh I B, Shpungin Y. Models of Network Reliability:Analysis, Combinatorics, and Monte Carlo[M]. Boca Rato, Florida, USA, CRC Press, 2009 [Google Scholar]
- Kamalja K K, Amrutkar K P. Reliability and Reliability Importance of Weighted-r-within-Consecutive-k-out-of-n:F System[J]. IEEE Trans on Reliability, 2018, 67(3): 951–969 [Article] [CrossRef] [Google Scholar]
- Birnbaum Z W. On the Importance of Different Components in a Multicomponent System Multivariate AnalysisⅡ[M]. New York, Academic Press, 1969: 581–592 [Google Scholar]
- Vesely W E. A Time-Dependent Methodology for Fault Tree Evaluation[J]. Nuclear Engineering and Design, 1970, 13(2): 337–360 [Article] [CrossRef] [Google Scholar]
- Fussell J B. How to Hand-Calculate System Reliability and Safety Characteristics[J]. IEEE Trans on Reliability, 1975, 24(3): 169–174 [Article] [CrossRef] [Google Scholar]
- Bhattacharya D, Roychowdhury S. Bayesian Importance Measure-Based Approach for Optimal Redundancy Assignment[J]. American Journal of Mathematical and Management Sciences, 2016, 35(4): 335–344 [Article] [CrossRef] [Google Scholar]
- Dui Hongyan, Si Shubin, Richard C M Y. A Cost-Based Integrated Importance Measure of System Components for Preventive Maintenance[J]. Reliability Engineering & System Safety, 2017, 168: 98–104 [Article] [CrossRef] [Google Scholar]
- Si Shubin, Yang Liu, Cai Zhiqiang, et al. A New and Efficient Computation Method of IM (Integrated Importance Measures) for Components in Binary Coherent Systems[J]. Journal of Northwestern Polytechnical University, 2011, 29(6): 939–947 [Article] [Google Scholar]
- Kuo W, Prasad V R, Tillman F A, et al. Optimal Reliability Design:Fundamentals and Applications[M]. Cambridge, UK, Cambridge University Press, 2006 [Google Scholar]
- Boland P J, Proschan F, Tong Y L. Optimal Arrangement of Components via Pairwise Rearrangements[J]. Naval Research Logistics, 1989, 36(6): 807–815 [Article] [CrossRef] [Google Scholar]
- Page L B, Perry J E. Reliability Polynomials and Link Importance in Networks[J]. IEEE Trans on Reliability, 1994, 43(1): 51–58 [Article] [CrossRef] [Google Scholar]
- Hsu S J, Yuang M C. Efficient Computation of Marginal Reliability-Importance for Reducible Networks[J]. IEEE Transactions on Reliability, 2001, 50(1): 98–106 [Article] [CrossRef] [Google Scholar]
- Hong J S, Lie C H. Joint Reliability-Importance of Two Edges in an Undirected Network[J]. IEEE Trans on Reliability, 1993, 42(1): 17–23 [Article] [CrossRef] [Google Scholar]
- Du Y J, Si S B, Gao H Y, et al. Birnbaum Importance Measure of Network Based on C-Spectrum under Saturated Poisson Distribution[C]//2017 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 2017: 934–938 [Article] [Google Scholar]
- Du Yongjun, Hou Peiyong, Guo Yaqi. Network Birnbaum Importance Measure under Saturated Poisson Distribution[J]. Journal of Northwestern Polytechnical University, 2017, 35(5): 870–875 [Article] [Article] [Google Scholar]
- Gertsbakh I, Shpungin Y. Network Reliability Importance Measures:Combinatories and Monte Carlo Based Computations[J]. WSEAS Trans on Computers, 2008, 7(4): 216–227 [Article] [Google Scholar]
- Gertsbakh I B, Shpungin Y. Combinatorial Approach to Computing Component Importance Indexes in Coherent Systems[J]. Probability in the Engineering and Informational Sciences, 2012, 26(1): 117–128 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图 1 立方体网络H3, K={1, 3, 6} |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


