| Issue |
JNWPU
Volume 37, Number 5, October 2019
|
|
|---|---|---|
| Page(s) | 943 - 951 | |
| DOI | https://doi.org/10.1051/jnwpu/20193750943 | |
| Published online | 14 January 2020 | |
Joint Optimization of User Association and Resource Allocation for Millimeter-Wave Integrated Backhaul and Access Network
5G毫米波回传与接入一体化网络中用户关联与资源分配联合优化方法
1
School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710072, China
2
College of Electronic Information Engineering, Lanzhou Institute of Technology, Lanzhou 730050, China
Received:
26
October
2018
Since the millimeter wave integrated backhaul and access network(mm-Wave IBAN) can divide the resource ratio between the access and the backhaul link as needed, there is a huge advantage in the improvement of the utilization rate for 5G communication network. A joint optimization method of user association and resource allocation is proposed and implemented for the mm-Wave IBAN from the perspective of the maximization of the transmission traffic in the whole network. The joint optimization problem of the user association and the resource allocation is formulated as a combined non-convex optimization problem, and then the problem is decomposed into two sub-problems. The first sub-problem, which is aimed at the maximization of the whole access rate, is the problem of the user association under the condition of the match between the access rate and backhaul rate. The second sub-problem, which is aimed at the maximization of the whole traffic of the network, is the problem of the resources allocation between the access link and backhaul link. The artificial immune optimization algorithm (IOA) is used to solve the first sub-problem. After that, the optimal transmission resource ratio between the access link and backhaul link is obtained according to the differentiating of the expression for the whole traffic. The simulation results show that the proposed method has more gains in the improvement of the whole network traffic when compared with the user association mechanism based on the nearest distance.
摘要
由于毫米波回传与接入一体化网络 (mm-Wave IBAN) 能够按需划分接入和回传链路之间的资源比例而在提升5G通信网络资利用率方面有巨大优势。从最大化全网传输业务量的角度出发提出并实现一种mm-Wave IBAN用户关联和资源分配的联合优化方法。首先将mm-Wave IBAN中用户关联和资源分配的联合问题建模为一个组合非凸优化问题,然后将其分解为2个子问题,即在接入速率和回传速率匹配约束情况下以全网接入速率最大化为目标的用户关联子问题(即子问题1)和以传输业务最大化为目标的接入与回传时间资源比例分配的子问题(即子问题2)。利用人工免疫优化算法求解子问题1,再通过对全网业务量表达式求导而得各小区接入和回传链路上的最优传输时间比例。仿真结果表明:与基于最近距离用户关联机制相比,在提升网络吞吐量方面有更大增益。
Key words: 5G millimeter wave / integrated backhaul and access network (IBAN) / user association / resource allocation / immune optimization
关键字 : 5G毫米波 / 回传与接入一体化 / 用户关联 / 资源分配 / 免疫优化
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
现有技术方案在解决提升5G系统吞吐量方面的问题时主要从两方面着手:一方面, 通过部署低能耗、高密集的微小区(small cell, SC)以提升频谱利用率, 形成超密集部署网络(ultra-dense deployment network, UDN); 另一方面, 使用可用带宽更大的毫米波(30~300 GHz)通信[1-1]。将毫米波通信与UDN技术相结合即形成了毫米波超密集部署网络。显然, 让每个微小区基站(small-cell base station, SBS)通过光纤进行数据回传在成本上是无法估量的。因此, 业内提出使用毫米波无线回传进而形成毫米波无线回传与接入一体化网络(millimeter-wave integrated backhaul and access network, mm-Wave IBAN), 其典型特征就是接入和回传链路共享无线资源[3]。
mm-Wave IBAN接入与回传链路之间的无线资源复用的方式有2种:①全双工共享时域和频域资源, 但使用该方式的技术瓶颈在于自干扰消除; ②单独地在时域或者频域共享资源, 即时分复用模式(time division multiplexing, TDM)或频分复用模式(frequency division multiplexing, FDM)[4]。但是, FDM在基于空间复用的点对点传输场景中的频谱利用率受限, 因此TDM是一种更为有效的方式。在mm-Wave IBAN的接入和回传链路之间使用TDM的方式有2种:①异步方式, 即SBS可按需独立地分配其接入和回传链路间的时间比例, 其特点在于系统灵活性强、资源利用率高, 但系统控制较为复杂; ②同步方式, 即要求全网所有SBS的接入和回传时间比例统一, 虽然全网统一地接入回传时间分配比例未必有利于每个SBS最大化其自身的吞吐量, 但其优势在于系统控制简单、可有效避免SBS接入时间与其他SBS回传时间重叠而造成的干扰。因此, 本文主要针对基于时间同步的mm-Wave IBAN, 确定使全网传输业务最大化的用户关联和资源分配方法。
在mm-Wave IBAN设计与优化方面, 现有文献往往从移动性管理[5-5]、路径选择[7-7]、资源调度[9-9]、回传路径规划[11-11]等多方面进行设计与优化, 而文献[13]最新调研了mm-Wave IBAN优化设计中面临的关键挑战与问题, 并讨论了mm-Wave IBAN网络标准化和部署的进展。实际上, mm-Wave IBAN的用户关联往往和其网络负载、资源利用等方面有较强的关联性而成为网络联合优化与设计的研究热点[14]。文献[15]研究了用户关联和功率分配的联合优化问题; 文献[16]中Ma等人研究了大规模多输入多输出(multiple-input multiple-output, MIMO)系统网络中的用户关联和资源分配问题, 实现回传容量受限的α公平网络效用的最大化。文献[17]中Ren等人在假设SBS有缓存支持功能的前提下, 研究了IBAN的用户关联和资源分配联合优化问题; Mesodiakaki等人在文献[18]中提出了多跳回传网络用户关联和频谱分配联合优化方法, 实现了能量效率和频谱效率的最大化。Feng等人在文献[19]中研究了大规模MIMO异构网络中帧结构、资源分配和用户关联的联合优化与设计问题, 并在无线回传速率和公平感知的约束条件下实现了所有用户总下行链路速率的最大化。但是, 文献[16-19]在处理用户关联与资源分配的联合问题时仅考虑接入层面的约束因素, 并未充分考虑接入和回传层面互耦合特性, 从而并未充分挖掘回传链路与接入联络之间的网络资源动态分配的性能增益。为了解决该问题, 提出一种mm-Wave IBAN中用户关联和资源分配的联合优化方法, 并将联合优化问题分解为用户关联子问题(即子问题1, 在SBS接入速率和回传速率匹配的情况下, 使全网SBS的接入速率最大化的问题)和资源分配子问题(即子问题2, 有效分配SBS的接入链路与回传链路的时间资源比例, 最大化全网SBS的传输业务量)。利用免疫优化算法求解子问题1后再通过对全网业务量表达式求导获得子问题2的解, 进而实现mm-Wave IBAN中传输业务量最大化的用户关联与资源分配联合优化。
1 系统模型
本文使用文献[20]中的用户数据平面与信令控制平面为相互分离的网络架构。其中, 控制平面负责控制信令传输, 数据平面负责业务传输, 本文主要聚焦于数据平面, 不涉及控制平面的内容。系统采用同步TDM方式, 即每个单位传输时间间隔(unit transmission interval, UTI)被划分为回传时间和接入时间, 且UTI内全网各SBS的接入和回传时间比例都是统一的。每个UTI的长度固定, 但不同UTI之间全网SBS的接入和回传时间比率根据网络用户移动情况动态变化。从数据传输方向上, 可将mm-Wave IBAN中的传输阶段分为上行接入、上行回传、下行回传、下行接入等阶段。由于网络下行运行机制和上行运行机制对称一致, 本文仅主要针对下行传输场景进行用户关联与资源分配的联合优化, 但本文的联合优化方法在上行传输场景中也同样适用。
假设网络中有1个毫米波宏基站(macro base station, MBS), MBS通过光纤传输的方式连接至核心网, 在MBS的覆盖范围内分布着N个毫米波微站(SBS), 其集合表示为N={1, 2, …, N}。M个用户(user equipment, UE), 其集合表示为M={1, 2, …, M}。其中, MBS通过毫米波无线通信将数据一跳传输至网络中的各SBS, 各SBS再将数据传输到关联至其上的各UE。在每个SBS通信资源总量一定的情况下, 各SBS的接入链路和回传链路共享通信资源。此外每个SBS在接入时间内都能为关联至其内的每个用户波束赋形一个通信波束, SBS和UE的波束赋形模型采用文献[21]中的扇区模型, 如图 1所示。该模型刻画了二维空间中实际波束的主要特征, 如方向增益、前后比、半功率带宽等。
理想天线模型中, 主瓣定向增益为较大的恒定常数, 而旁瓣定向增益为较小的恒定常数。为简化计算, 假设网络中所有SBS的主瓣波束宽度是相等的常数。用γn, msc(n∈N, m∈M)表示第n个微小区基站SBSn的波束视轴角(即SBSn的主瓣波束中心对称轴与水平正轴方向的夹角), γn, mue(n∈N, m∈M)表示第m个用户UEm的波束视轴角(即UEm的主瓣波束中心对称轴与水平正轴方向的夹角)。用τn, msc(n∈N, m∈M)表示从SBSn处到UEm处的方向向量与水平正轴之间的夹角, τn, mue(n∈N, m∈M)表示从UEm处到SBSn处的方向向量与水平正轴之间的夹角; θnsc(n∈N)表示SBSn的波束宽度, θmue(m∈M)表示UEm的波束宽度。另外, 分别用gn, msc(n∈N, m∈M)和gn, mue(n∈N, m∈M)表示SBSn和UEm之间定向发送增益和定向接收增益, 利用图 1中的波束模型, 可将发送点SBSn的定向发送增益gn, msc表示为
式中, Scn是旁瓣增益, 当波束非常细时则。同理, 接收点UEm的定向接收增益SCn可表示为
因此, 在用户UEm处接收到其所关联的SBSn的信干噪比(signal to interference plus noise ratio, SINR)SINRn, m可表示为
式中, pnsc表示SBSn的发送功率(在单位传输间隔UTI内, 假定该值是一个恒定的常数); gn, mh表示SBSn与UEm之间信道增益, gn, mh主要建模描述SBSn和UEm之间链路上的路径损耗和阴影效应; No表示网络背景噪声功率。
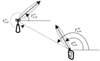 |
图 1 节点天线模型图 |
2 问题描述
用xn, m表示UEm是否被关联至SBSn的决策变量(xn, m=1表示UEm关联至SBSn, xn, m=0则表示UEm未被关联至SBSn)。对于任意的UEm只能与网络中的一个SBSn关联, 而任意的SBSn可关联多个UEm, 因此有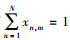 ; 假设传输时间间隔UTI为t, tnAC表示SBSn在该传输时间间隔内的接入时间, tnBH表示SBSn在该传输时间间隔内的回传时间, tnAC+tnBH=t。W表示传输带宽, 则SBSn在UTI内的回传业务量TnBH可以表示为
; 假设传输时间间隔UTI为t, tnAC表示SBSn在该传输时间间隔内的接入时间, tnBH表示SBSn在该传输时间间隔内的回传时间, tnAC+tnBH=t。W表示传输带宽, 则SBSn在UTI内的回传业务量TnBH可以表示为
SBSn在UTI内的接入业务量TnAC可表示为
式中, SINRn, o为SBSn与宏基站MBS之间的信干噪比。对于SBSn, 在传输时间间隔UTI内实际能够传输的业务量Tn取决于其回传业务量TnBH和接入业务量TnAC的最小值, 即
因此mm-Wave IBAN中, 以全网传输业务量最大化为目标的用户关联和资源分配联合优化问题可被建模为问题Qp
Qp中, C1是关于用户关联的约束条件, C2-C3是关于SBS和UE波束视轴角变量的约束条件, C4为资源分配有关的约束, 该约束表明对于任意的SBSn, 其下行接入时间与回传时间的总和为给定的传输时间间隔时间t。通过分析, 可将Qp定性为非凸组合优化问题, 其组合性是主要体现在约束条件C1中, 而非凸性主要体现在约束条件C2-C3, 这是一个NP-hard问题, 很难直接求解。因此, 将Qp分解为2个子问题, 并依次求解每个子问题, 以求获得的Qp次优解。
3 问题求解
3.1 基于免疫优化的用户关联算法
实际上, 由于对于拓扑给定的mm-Wave IBAN是一个静态的网络, 即SBSn与宏基站MBS之间的回传速率在主要取决于SBSn与宏基站之间的路径损耗, 因此可假定SBSn与MBS之间的回传链路速率是稳定不变的。由文献[22]中的分析可知:就mm-Wave IBAN中的任意微小区基站SBSn而言, 当SBSn的接入速率RnAC (∀n∈N)和回传速率RnBH (∀n∈N)相匹配时, 其传输业务量Tn可达到最大值。因此, 为了使网络中各微小区基站SBSn(1≤n≤N)的接入速率RnAC (∀n∈N)与其回传速率RnBH (∀n∈N)相匹配, 特引入一个新的约束条件, 即R1AC:R2AC:…:RnAC=R1BH:R2BH:…:RnBH, 则mm-Wave IBAN下行接入速率最大化问题可建模为问题QP1
其中, C1-C3的物理意义与QP中的相同, C4表示各SBSn(∀n∈N)的无线接入速率RnAC与其回传速率RnBH的匹配约束。由于免疫优化算法(immune optimization algorithm, IOA)在求解非凸优化问题和非线性多目标优化问题时克服了一般寻优过程难以处理的“早熟”问题(即过早地求得局部最优解而失去全局最优解的问题), 从而能够最终求得全局最优解。因此使用IOA对QP1进行求解。
IOA算法在最优解搜索过程主要依赖于5个重要的元素, 即抗原、抗体、浓度、克隆和适应度。其中, 抗原代表所要解决的问题(具体表现为目标函数, 本文中主要表示全网总接入速率的函数表达式); 抗体代表问题所对应欧式空间中的可行解(具体表现为一个具有真值属性的字符串, 本文中主要表示由用户关联变量xn, m, SBSn与UEm波束视轴角γn, msc, γn, mue所构成的编码字符串); 浓度代表抗体多样性的度量(具体表现为编码后的抗体群中各抗体取值相同的位置数); 克隆代表子代抗体完全复制父代抗体(具体表现为子代字符串完全复制父字符串); 适应度代表抗体与抗原的适应性(具体表现抗体所代表的解与抗原所代表的目标函数的匹配程度)及抗体与抗体的适应性(具体表现为抗体与抗体的匹配程度, 即各解之间的相似程度); 在本文中, 一个抗体代表用户关联变量xn, m, SBSn与UEm的主瓣视轴角度变量γn, msc和γn, mue的联合可行解, 具体的IOA算法抗体编码如图 2所示。
抗体种群中, 第i个抗体的期望繁殖概率Pi同时取决于亲和度函数Ai和抗体浓度函数Ci
式中, ε为多样性估计参数, Sc为抗体种群大小, Pi表示用户关联决策变量xn, m, SBSn与UEm波束视轴角变量γn, msc和γn, mue组成的抗体种群的繁殖概率, Ai是第i个抗体的亲和度, Ci是第i个抗体的相似比例, 即浓度。亲和度函数Ai定义为
式中, β为一个很大的正常数, Y(0≤Y<1)为SBSn测量接入速率RnAC与其回传速率RnBH匹配程度的匹配指数, 具体如(11)式所示。那么, β(1-Y)代表违反QP1中C4的罚函数。
代表抗体种群中相似比例的抗体浓度Ci为
式中,Tii′代表抗体种群中的相似度, 其具体定义如(13)式所示
Th是预先定义的相似度阈值, Sii′代表第i个抗体和第i′个抗体编码中取值相同的位置数
式中, bij 和bi′j表示第i个抗体和第i′个抗体的第j位的值。
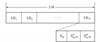 |
图 2 抗体编码图 |
3.2 资源分配算法
在不考虑同步TDM约束条件的情况下, 对于mm-Wave IBAN中的任意某个微小区基站SBSn而言, 将(4)~(5)式带入(6)式中可得SBSn在UTI内的传输业务量Tn(tnBH)的表达式为
从(15)式可以看出, Tn(tnBH)是一个以回传时间tnBH为自变量的分段线性三角函数。将该函数取最大值时的回传时间称为最佳回传时间tn, optBH。通过分析可得, Tn(tnBH)首先以斜率RnBH呈线性增长趋势, 这时SBSn的回传业务量TnBH小于接入业务量TnAC, 即SBSn的整体传输业务量处于回传受限的状态; 当SBSn的回传时间tnBH达到最佳回传时间tn, optBH时(即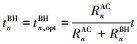 ), 函数Tn(tnBH)的值达到最大, 即SBSn的整体传输业务量达到最大值。此后, Tn(tnBH)以斜率RnAC降低, 这时SBSn的接入业务量TnAC小于回传业务量TnBH, 即SBSn的整体传输业务量处于接入受限的状态。因此, 对于任意的SBSn而言, 其最佳回传时间tn, optBH和最佳接入时间tn, optAC可表示为
), 函数Tn(tnBH)的值达到最大, 即SBSn的整体传输业务量达到最大值。此后, Tn(tnBH)以斜率RnAC降低, 这时SBSn的接入业务量TnAC小于回传业务量TnBH, 即SBSn的整体传输业务量处于接入受限的状态。因此, 对于任意的SBSn而言, 其最佳回传时间tn, optBH和最佳接入时间tn, optAC可表示为
由于不同SBSn的接入速率RnAC和回传速率RnBH是相互不同的, 因此不同SBSn在UTI内的传输业务量Tn(tnBH)所达到极值时所对应的最佳回传时间tn, optBH和最佳接入时间tn, optAC也是不同的。但是, 为了避免某些SBS的回传传输对另外一些SBS的接入传输SBSn的干扰, 在采用同步TDM的mm-Wave IBAN中要求所有SBS的回传时间tBH是相同的。通过对子问题1的求解, 即获得了使mm-Wave IBAN全网总接入速率最大化的SBS的接入速率和回传速率。在此基础上, 通过对子问题2的求解, 即找到全网SBS统一使用的、并使全网传输业务量达到最大化的接入链路与回传链路之间的时间资源比例有效分配方法。
首先, 将所有SBS各自的理论最佳回传时间tn, optBH按照从小到大的顺序进行排序, 设经过排序后的最佳回传时间序列为[t1, optBH, t2, optBH, …, tN, optBH], 其中t1, optBH和tN, optBH分别表示所有SBS的最佳回传时间中的最小值和最大值, 即
与[t1, optBH, t2, optBH, …, tN, optBH]所对应的各SBS的回传速率序列表示为[R1BH, R2BH, …, RNBH], 接入速率序列表示为[R1AC, R2AC, …, RNAC]。
然后, 假定一个回传时间区间[tl*-1BH, tl*BH], 该区间使得所有SBS的(l*-1)个SBS是接入受限的, (N-(l*-1))个SBS是回传受限的, 则全网总传输业务量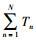 的一般表达式可表示为
的一般表达式可表示为
(18) 式本质上是一种分段线性三角和函数且有tuniBH ∈[tl*-1BH, tl*BH]。由分段线性三角和函数最大化的相关理论可知, 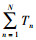 的峰值将出现在区间[tl*-1BH, tl*BH]的端点上, 那么问题的关键就是找出l*。通过对
的峰值将出现在区间[tl*-1BH, tl*BH]的端点上, 那么问题的关键就是找出l*。通过对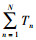 关于tuniBH求偏微分来确定l*需要满足的条件, 即:
关于tuniBH求偏微分来确定l*需要满足的条件, 即:
但是, 考虑到l*应该是一个整数, 那么最终通过序列[Rl*BH, Rl*+1BH, …, RNBH]和[Rl*BH, Rl*+1BH, …, RNBH]确定的l*应该满足的条件是使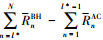 取值为正且最小, 依据该条件我们就能够确定区间[tl*-1BH, tl*BH], 从而获得(18)式的解, 即使全网总传输业务量最大化并在各SBS中统一使用的最佳回传时间tuniBH。这说明区间[tl*-1BH, tl*BH]是
取值为正且最小, 依据该条件我们就能够确定区间[tl*-1BH, tl*BH], 从而获得(18)式的解, 即使全网总传输业务量最大化并在各SBS中统一使用的最佳回传时间tuniBH。这说明区间[tl*-1BH, tl*BH]是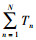 的最后一段增区间, 因此选择tuniBH=tl*BH。
的最后一段增区间, 因此选择tuniBH=tl*BH。
4 仿真分析
为仿真验证本文所提出的联合优化算法性能, 我们将联合优化算法与现有文献中普遍使用的基准算法[11, 17, 23](即基于最近距离的用户关联算法)进行对比分析。为公平起见, 基准算法中的关联决策变量由每个用户接入到距离自己最近的SBS所确定, 而在求解SBS及UE的波束视轴角变量时也采用IOA算法。
仿真中, 设置每个SBS的覆盖范围内有4个随机分布的用户, 所有SBS都部署在MBS的覆盖范围中, MBS和各SBS的发送功率都是恒定的; 抗体种群数量为30, 抗体记忆内存为10, 交叉概率pc和变异概率pm分别为0.5和0.4;算法中使用转轮盘法进行抗体的选择, 并用与繁殖概率成比例的概率进行抗体个体选择; 算法根据随机均匀分布的方式来选择抗体交叉的基因位置, 并随机选择抗体字符串中的一个位置作为变异位。算法仿真中所用到的其他主要参数在表 1中给出。
图 3是最大迭代次数Lmaxiteration=400时的算法收敛性曲线。图 3中的最优适应度值是每轮迭代中根据(10)式对所有抗体计算后所得各值中的最小值; 平均适应度是每轮迭代中所有抗体适应度的平均值。从图中可以明显看出; 基于IOA的求解算法大约经过260次迭代即可求得稳定的最优解, 基于IOA的用户关联求解算法有很好的收敛性。
图 4给出了当网络中SBS数为50时, 本文算法和基于最近距离接入的算法中全网各SBS的接入吞吐量、回传吞吐量的累计分布函数(cumulative distribution function, CDF)图。观察图 4中可得出以下结论:①由于网络中各SBS和MBS之间的路径损耗和阴影衰落不同, 因此各SBS之间的回传吞吐量存在差异, 即有些SBS的回传吞吐量较大(距离MBS较近), 有些SBS的回传吞吐量较小(距离MBS较远), 具体表现为图 4b)中本文提出算法的CDF曲线的增长趋势; ②相对于基于最近距离关联算法, 本文提出的算法的各SBS的接入吞吐量更大, 具体表现为图 4a)中本文提出算法的CDF曲线相对于基于最近距离关联算法的CDF曲线整体右移; ③与基准算法相比, 本文提出的算法中各SBS的接入吞吐量和回传吞吐量匹配度较高, 即回传吞吐量和接入吞吐量之间的差值相对较小, 具体表现为, 图 4a)和图 4b)中本文提出算法的接入吞吐量和回传吞吐量CDF曲线整体匹配相对集中, 即2~8 Gb·s-1之间; 而基于最近距离算法的回接入吞吐量与回传吞吐量CDF曲线整体匹配相对分散, 即基于最近距离算法的接入吞吐量在2 Gb·s-1以下, 而回传吞吐量却大多在2~12 Gb·s-1之间, 这也侧面表明为回传吞吐量较大的SBS关联更多用户, 使得网络负载更加均衡, 从而提升全网传输业务量。
从图 5是当网络中SBS数为50时SBS端到端吞吐量CDF图。从图中可以看出:基于最近距离关联算法中各SBS的吞吐量大多在2 Gb·s-1以下, 本文所提出算法各SBS吞吐量大多在2~9.16 Gb·s-1之间, 即本文所提出的联合优化算法在各SBS的实际端到端吞吐量方面性能更优。这是因为网络中各SBS的实际吞吐量取决于各SBS的回传吞吐量和接入吞吐量二者中的较小者, 本文提出算法使得用户尽量接入回传容量较大的SBS, 以此降低SBS的接入吞吐量和回传吞吐量差异, 使其达到相匹配, 从而整体提升端到端吞吐量。
图 6给出了给定覆盖区域中全网总吞吐量与网络中SBS数量的关系变化图。从图中可以看出:当网络SBS数量为100时, 本文提出算法的网络总吞吐量比基于最近距离用户关联算法的网络总吞吐量高出近38%;随着网络中SBS数量的不断增加, 全网总吞吐量呈下降趋势, 这是因为随着网络节点密度的不断增加, 毫米波波束之间的干扰也不断增加, 网络从噪声受限网络变为干扰受限网络, 引起网络性能下降。尽管如此, 但是当SBS数量增加到200时, 本文提出的联合优化算法的网络总吞吐量比基于最近距离关联算法的网络总吞吐量还高15.3%。
算法仿真参数设置
 |
图 3 算法收敛性 |
 |
图 4 网络中各SC的接入吞吐量和回传吞吐量 |
 |
图 5 网络中SC端到端吞吐量的CDF |
 |
图 6 网络总吞吐量与网络SC数关系变化图 |
5 结论
提出了mm-Wave IBAN中一种最大化网络吞吐量的用户关联和资源分配联合优化方法。首先用IOA算法求解用户关联决策变量、SC与用户的波瓣视轴角变量, 然后通过对总吞吐量一般表达式求导计算出SC接入链路和回传链路之间的最优时间分配比例, 最后用仿真证明了本文提出算法的收敛性和有效性。仿真结果表明:本文算法尽可能使用户与回传容量大的SC相关联, 使SC接入速率与回程速率相匹配, 从而使各SC吞吐量和全网总吞吐量也得以显著提高。本文仅研究了同步TDM模式下的用户关联与资源分配的联合优化方法, 今后将进一步研究异步TDM模式下mm-Wave IBAN中的用户关联与资源分配联合优化方法。
References
- OLWAL T O, DJOUANI K, KURIEN A M, et al. A Survey of Resource Management toward 5G Radio Access Networks[J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 1656–1686 [Article] [CrossRef] [Google Scholar]
- PI Z, CHOI J, HEATH R. Millimeter-Wave Gigabit Broadband Evolution toward 5G:Fixed Access and Backhaul[J]. IEEE Communications Magazine, 2016, 54(4): 138–144 [Article] [CrossRef] [Google Scholar]
- ISLAM M N, SUBRAMANIAN S, SAMPATH A, et al. Integrated Access Backhaul in Millimeter Wave Networks[C]//2017 IEEE Wireless Communications and Networking Conference, San Francisco, 2017: 1–6 [Google Scholar]
- MARSCH P, et al. 5G Radio Access Network Architecture:Design Guidelines and Key Considerations[J]. IEEE Communications Magazine, 2016, 54(11): 24–32 [Article] [CrossRef] [Google Scholar]
- CACCIAPUOTI A S. Mobility-Aware User Association for 5G MmWave Networks[J]. IEEE Access, 2017, 521497–21507 [Article] [CrossRef] [Google Scholar]
- RONY R I, JAIN A, LOPEZ-AGUILERA E, et al. Joint Access-Backhaul Perspective on Mobility Management in 5G Networks[C]//Standards for Communications and Network, 2017 [Google Scholar]
- SAADAT S, CHEN D, JIANG T. Multipath Multi-Hop Mm-Wave Backhaul in Ultra-Dense Small-Cell Network[J]. Digital Communications and Networks, 2018, 4(2): 111–117 [Article] [CrossRef] [Google Scholar]
- POLESE M, GIORDANI M, ROY A, et al. Distributed Path Selection Strategies for Integrated Access and Backhaul at mm-Waves[OL]. ArXiv Preprint ArXiv: 1805.04351, <a href="https://arxiv.org/abs/1805.04351" target="_blank">https://arxiv.org/abs/1805.04351</a> [Google Scholar]
- LI J, ZHU Y, WU D O. Practical Distributed Scheduling for QoS-Aware Small Cell mm-Wave Mesh Backhaul Network[J]. Ad Hoc Networks, 2017, 5562–71 [Article] [CrossRef] [Google Scholar]
- YAO Y, TIAN H, NIE G, et al. Coloring Based Access-Backhaul Scheduling in Ultra Dense Networks with Flexible Duplex[C]//2018 IEEE Wireless Communications and Networking Conference, 2018: 1–6 [Google Scholar]
- ZOLA E, KASSLER A J, KIM W. Joint User Association and Energy Aware Routing for Green Small Cell Mm-Wave Backhaul Networks[C]//2017 IEEE Wireless Communications and Networking Conference, 2017: 1–6 [Google Scholar]
- HUERFANO D, DEMIRKOL I, LEGG P. Joint Optimization of Path Selection and Link Scheduling for Millimeter Wave Transport Networks[C]//2017 IEEE International Conference on Communications Workshops, 2017: 115–120 [Google Scholar]
- XIAO M, MUMTAZ S, HUANG Y, et al. Millimeter Wave Communications for Future Mobile Networks[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 1909–1935 [Article] [CrossRef] [Google Scholar]
- SHOKRI-GHADIKOLAEI H, FISCHIONE C, FODOR G, et al. Millimeter Wave Cellular Networks:a MAC Layer Perspective[J]. IEEE Trans on Communications, 2015, 63(10): 3437–3458 [Article] [CrossRef] [Google Scholar]
- YANG K, WANG L, WANG S, et al. Optimization of Resource Allocation and User Association for Energy Efficiency in Future Wireless Networks[J]. IEEE Access, 2017, 516469–16477 [Article] [CrossRef] [Google Scholar]
- MA H, ZHANG H, WANG X, et al. Backhaul-Aware User Association and Resource Allocation for Massive MIMO-Enabled HetNets[J]. IEEE Communications Letters, 2017, 21(12): 2710–2713 [Article] [CrossRef] [Google Scholar]
- REN G, QU H, ZHAO J, et al. A Distributed User Association and Resource Allocation Method in Cache-Enabled Small Cell Networks[J]. China Communications, 2017, 14(10): 95–107 [Article] [CrossRef] [Google Scholar]
- MESODIAKAKI A, ADELANTADO F, ALONSO L, et al. Energy-and Spectrum-Efficient User Association in Millimeter-Wave Backhaul Small-Cell Networks[J]. IEEE Trans on Vehicular Technology, 2017, 66(2): 1810–1821 [Article] [CrossRef] [Google Scholar]
- FENG M, MAO S, JIANG T. Joint Frame Design, Resource Allocation and User Association for Massive MIMO Heterogeneous Networks with Wireless Backhaul[J]. IEEE Trans on Wireless Communications, 2017 991–16 [Article] [Google Scholar]
- SIDDIQUE U, TABASSUM H, HOSSAIN E. Downlink Spectrum Allocation for In-Band and Out-Band Wireless Backhauling of Full-Duplex Small Cells[J]. IEEE Trans on Communication, 2017, 65(8): 3538–3554 [Article] [CrossRef] [Google Scholar]
- Zhuang H, Chen J, Wu D O, et al. Joint Access and Backhaul Resource Management for Ultra-Dense Networks[C]//2017 IEEE International Conference on Communications, Paris, 2017: 1–6 [Google Scholar]
- SHI Z, WANG Y, HUANG L, et al. Dynamic Resource Allocation in Mm-Wave Unified Access and Backhaul Network[C]//International Symposium on Personal, Indoor, and Mobile Radio Communications, 2015: 2260–2264 [Google Scholar]
- LIU D, WANG L, CHEN Y, et al. User Association in 5G Networks:a Survey and an Outlook[J]. IEEE Communications Surveys & Tutorials, 2015, 18(2): 1018–1044 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图 1 节点天线模型图 |
| In the text | |
 |
图 2 抗体编码图 |
| In the text | |
 |
图 3 算法收敛性 |
| In the text | |
 |
图 4 网络中各SC的接入吞吐量和回传吞吐量 |
| In the text | |
 |
图 5 网络中SC端到端吞吐量的CDF |
| In the text | |
 |
图 6 网络总吞吐量与网络SC数关系变化图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


