| Issue |
JNWPU
Volume 37, Number 5, October 2019
|
|
|---|---|---|
| Page(s) | 935 - 942 | |
| DOI | https://doi.org/10.1051/jnwpu/20193750935 | |
| Published online | 14 January 2020 | |
L1 Adaptive for Aircraft Lateral Fault Tolerant Control with Actuator Failure
带执行器故障的L1自适应飞行器横侧向容错控制
1
School of Automation, Northwestern Polytechnical University, Xi'an 710129, China
2
School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, China
Received:
8
November
2018
When aircraft is laterally controlled, actuator failure may cause matched/unmatched uncertainties. In order to deal with the uncertainty, a fault-tolerant controller is designed by using L1 adaptive control method. An aircraft lateral model was established by considering faults and disturbances, the effects of the uncertainty and interference were counteracted by using L1 adaptive controller in order to ensure the rapid adaptation and robustness, and then the stability and transient performance of the closed-loop system were proven through Lyapunov method. In the case of multiplicative fault, additive fault and stuck fault, the uncertainties of model parameter were added to simulate simultaneously. Simulation results showed that the present control method in both single-fault mode and hybrid-failure mode could ensure the uniform bounded control signal and parameter estimation, effectively eliminates the effect of the faults and had the good fault tolerance and robustness.
摘要
在飞行器横侧向控制中,执行器故障可能会引起匹配/非匹配不确定性,为了处理这种不确定性,采用L1自适应控制方法设计容错控制器。建立考虑故障和干扰的飞行器横侧向模型,利用L1自适应控制器抵消不确定性以及干扰的影响,保证快速自适应和鲁棒性,同时通过Lyapunov方法证明闭环系统的稳定性,并分析其暂态性能。在乘性故障、加性故障和卡死故障条件下,同时加入模型参数不确定性进行仿真,仿真结果表明,不论是在单一故障模式还是混合故障模式下所提控制方法均能保证控制信号和参数估计一致有界,有效抵消故障影响,具有良好的容错性和鲁棒性。
Key words: L1 adaptive control / actuator failure / lateral control / fault tolerant control / aircraft
关键字 : L1自适应控制 / 执行器故障 / 横侧向控制 / 容错控制 / 飞行器
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
飞行器所处环境复杂多变, 不可避免会发生故障, 如结构故障、执行器故障、传感器故障等。执行器故障是最常见的、危害性较大的一类故障, 须有及时有效的故障处理机制, 被动或主动的克服、抵消故障对闭环系统的影响, 使飞行器顺利完成飞行任务。
自适应方法能处理一定程度不确定性的特点使得它在飞行控制系统中得到了广泛应用。近年来, 国内外许多学者致力于自适应容错控制的研究[1-1]。Cao和Hovakimyan于2006年提出L1自适应控制, 通过引入低通滤波器来消除控制信号中的高频动态, 从而阻止高频振荡, 实现系统的快速自适应和鲁棒性[3-3]。目前, L1自适应控制广泛应用在四旋翼飞行器、直升机、战斗机、超音速飞行器等控制对象[2, 5-6]。文献[6]应用L1自适应和反步法设计外环位置控制器, 以抵消模型不确定和外部干扰的影响, 并产生内环控制器的参考姿态角信号和飞行器所需的推力。仿真与飞行实验验证了L1自适应反步控制器能实现任何两阶可微轨迹跟踪。文献[7]在飞机翼面部分损伤的情况下, 建立故障飞机模型并应用L1自适应控制重构控制器, 实现系统的快速响应和容错性。但飞机故障参数模型不易得到。文献[8]针对飞机舵面故障引起的匹配/非匹配不确定性设计L1自适应容错控制器, 但对飞行器故障模式缺少定性分析与处理。
相比纵向控制, 飞行器的横侧向控制更为复杂, 考虑故障的横侧向控制的相关研究较少。在文献[16]的启发下, 本文在执行器故障和外部干扰的条件下研究飞行器横侧向控制, 运用L1自适应方法设计控制器来抵消故障引发的匹配/非匹配不确定性的影响, 从而实现控制目标。
1 存在执行器故障的飞行器横侧向模型
飞行器横侧向动力学模型可写成
式中
x, u是状态变量和控制变量, β, p, r, φ分别为侧滑角、滚转角速度、偏航角速度和滚转角, δa, δr是副翼偏转角和方向舵偏转角, Q为动压, b, Sw, m, V分别为飞行器翼展长、翼参考面积、质量和速度, θ, α, q为俯仰角、迎角和俯仰角速度, c1-c9为力矩方程系数, Clβ, Cnβ为静稳定性导数, Clp, Cnr为阻尼导数, Clr, Cnp为交叉动导数, Clδa, Cnδa, Clδr, Cnδr为操纵导数, CYβ, CYp, CYr为侧力导数。
考虑以下故障模式和外部扰动
式中, ω∈R2×2(0<ωii≤1, i=1, 2)为对角阵, 表示各个执行器失效故障程度的控制因素矩阵。0<ωii<1表示该执行器发生部分失效故障, ωii=1表示该执行器正常工作, ωii=0表示执行器完全失去控制效力, 无法操纵的极端情况, 这里不予考虑。v∈R2×2是虚拟控制量, 当vi=const∈[δmin, δmax], δmin, δmax是δa, δr的极限位置, 此时表示执行器发生卡死或饱和故障。Δf∈R2×1是有界的加性故障, 本文讨论的ω, Δf均是常值或时变参数, d∈R2×1是有界的外部扰动。
为保证系统期望特性, 控制律可分成线性状态反馈控制律um=-KTx和自适应控制律uad两部分。令Am=A-BmKT, 其中A为系统线性部分。根据文献[9]可知, 经状态反馈得到的Am与A满足Erzberger模型完全跟踪条件。结合故障模式(2), 飞行器横侧向动力学模型(1)可转化为
式中, f表示系统不确定性、故障和干扰的总和, 分别为系统输入不确定性Bm(I-ω)KTx, 非线性不确定性f-Ax, 故障gΔf和干扰gd。
当执行器发生故障时, 系统将出现匹配/非匹配不确定性。故可将f分解为匹配不确定性fm和非匹配不确定性fum, 且考虑系统存在结构参数不确定性, (3)可表述为
式中, Am∈R4×4, Bm∈R4×2, Bum∈R4×2为已知的常数矩阵, 且(Am, Bm)可控, BmTBum=0, [Bm, Bum]满秩,  , ΔA表示系统结构参数不确定性。
, ΔA表示系统结构参数不确定性。
借鉴文献[10]中非线性函数转换思想, 本文在以下假设条件下对fm, fum进行转换:
假设1 当t>0时, 存在bi>0(i=1, 2)使得 。
。
假设2 ∀δ>0, 存在不依赖于时间的正常数dfmx(δ), dfumx(δ), dfmt(δ), dfumt(δ)使得非线性函数的偏导数是分段连续有界的, 即
当存在正常数ρ, dx, 同时‖xτ‖L∞≤ρ, 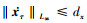 , 则对于任意的t∈(0, τ), θi, δi(i=1, 2)均是连续且导数有界的未知参数, 非线性函数可以写成
, 则对于任意的t∈(0, τ), θi, δi(i=1, 2)均是连续且导数有界的未知参数, 非线性函数可以写成
将(7)、(8)式代入, (4)式可改写为
自此, 存在执行器故障、外部干扰和模型参数不确定性的横侧向控制系统模型构建完成。本文的控制目标是, 设计一个L1自适应控制器, 在给定的参考信号作用下, 即使飞行器存在模型参数变化、执行器故障和外部扰动, 也能使得输出y跟踪所给标称系统的输出, 并保证其他信号的有界性。
2 L1自适应控制器的设计
本文设计的L1自适应控制器主要包括状态预测器、参数自适应律和控制律三部分。状态预测器估计系统状态响应; 在保证闭环系统稳定的前提下设计的自适应律对参数进行更新调整; 带低通滤波器的控制律根据调整后的参数及参考输入输出控制量, 以实现控制目标。
2.1 状态预测器
本文设计的状态预测器为
式中,  是系统状态变量、执行器控制因素矩阵、匹配/非匹配不确定性的参数和输出变量的估计值。
是系统状态变量、执行器控制因素矩阵、匹配/非匹配不确定性的参数和输出变量的估计值。
2.2 参数自适应律
状态预测器中参数的自适应更新律为
式中,  为自适应增益, 这里均取为Γ, P为对称正定矩阵, 是AmTP+PAm=-Q, Q=QT>0的解阵, proj(·)是投影算子符号, 保证参数的有界性。
为自适应增益, 这里均取为Γ, P为对称正定矩阵, 是AmTP+PAm=-Q, Q=QT>0的解阵, proj(·)是投影算子符号, 保证参数的有界性。
2.3 控制律
引入低通滤波器的L1自适应控制器控制律为
式中, k∈R2×2, D(s)是需要设计的低通滤波器参数。为了简便起见, D(s)设为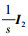 , 则低通滤波器为C(s)=ωk(s+ωk)-1。rg(s)=kgr(s)=
, 则低通滤波器为C(s)=ωk(s+ωk)-1。rg(s)=kgr(s)= 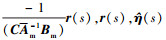 是r(t),
是r(t),  的拉普拉斯变换, 其中
的拉普拉斯变换, 其中
为确保闭环系统的稳定性, 反馈增益矩阵k应满足L1范数条件[16]
式中
3 L1自适应控制器的性能分析
3.1 稳定性分析
(10) 式减去(9)式得到系统预测误差状态方程
式中
并且ω, θi, δi(i=1, 2)满足以下边界条件
同时, 定义
考虑如下Lyapunov函数
首先, 观察到V(0)满足
其次, 根据预测误差状态方程(14), Lyapunov函数的导数为
∀t∈[0, τ1)(τ1∈(0, τ]), 根据(15)式和矩阵迹性质tr(AB)=tr(BA), XTAX=tr(XXTA), 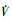 可化简为
可化简为
由参数的边界条件(16)可以得到
接下来证明Lyapunov函数具有单调下降性, 即 。假设
。假设 , ∀τ′∈(0, τ1), 将θm(ρr)的定义代入得到
, ∀τ′∈(0, τ1), 将θm(ρr)的定义代入得到
即
将(21)式代入(20)式, 整理得到
即
进而得到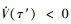 , 而由(18)式可知
, 而由(18)式可知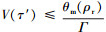 , 这与假设不相符。故
, 这与假设不相符。故 , 闭环系统是稳定的。且
, 闭环系统是稳定的。且 , 可得
, 可得
由(23)式可知, 预测误差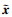 是有界的, 可通过增大自适应增益Γ来减小预测误差。
是有界的, 可通过增大自适应增益Γ来减小预测误差。
3.2 性能边界分析
为了分析L1自适应控制器的性能, 引入以下闭环参考系统
式中, η1ref(s), η2ref(s)是匹配、非匹配不确定性fm, fum的拉普拉斯变换。
首先, 令自适应增益Γ满足
式中, γ0为一任意小的正常数。
将(25)式代入(23)式, 得到
同时将(12)式改写为
式中, 是
是 的拉普拉斯变换。
的拉普拉斯变换。
其次, 将(9)式、(14)式和(24)式的状态方程写成频域形式为
式中, 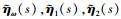 , 分别是
, 分别是 的拉普拉斯变换。
的拉普拉斯变换。
(28) 式减去(27)式, 得到
同时(29)式可改写为
将上式代入(30)式, 得到
因此有
定义L1ρr>dfx1(ρr(ρr)), L2ρr>dfx2(ρr(ρr)), 整理上式得到
设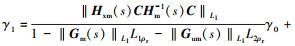 ε, ε是任意小的正常数。因此, 上式可简写为
ε, ε是任意小的正常数。因此, 上式可简写为
同理可得
式中
结合yref(t)=Cxref(t), 有
(26) 式和(31)~(33)式为闭环系统的性能边界。从边界条件可以看出增大自适应增益Γ可以实现任意小的性能边界。然而Γ受到有效CPU和传感器高频噪声的制约, 值过大会降低系统的鲁棒性, 因此需要选取合适的Γ兼顾系统性能和鲁棒性。
4 仿真验证
为了验证本文所提容错控制器的有效性, 分别就单一故障和混合故障2种模式对某无人机进行数字仿真。无人机的飞行高度H=5 000 m, 空速V0=12 m/s, 配平后的迎角α=0.117°, 升降舵舵偏δe=-2.590 5°。副翼和方向舵引入的外部扰动分别为cost, sint, 且考虑结构参数不确定性为10%, 参考输入信号为r(t)=1。
自适应参数的范围为
L1自适应控制器相关参数的选取如下
首先, 只考虑系统结构参数不确定性和外部干扰的情况, 系统输出曲线如图 1所示。
从图 1可以看出, 在系统存在结构参数不确定性和扰动的情况下, L1自适应控制器能快速准确地跟踪输入信号, 超调和跟踪误差均较小, 有效地消除了不良因素的影响, 保证系统的快速响应和稳定性。
其次, 在单一故障模式下的仿真结果及分析。这里主要讨论乘性故障、加性故障和卡死故障3种模式, 其中乘性和加性故障是常值或时变的, 分4种情况进行仿真验证:
故障 1 常值的乘性故障(故障因子分别为0.3, 0.8);
故障 2 时变的乘性故障(故障因子分别为0.5, t);
故障 3 加性故障(0.8+0.3sin0.1t, 0.2sin(10t+0.5));
故障 4 右副翼卡死在0°。
图 2~6是4种故障情况下的输出曲线、故障1时L1自适应容错控制器的控制信号和自适应参数估计曲线。
最后, 考虑几种故障模式混合情况。混合故障1为:无故障, 0 s≤t<10 s; 加性故障(0.5-2sin0.1t, -0.4sin10t), 10 s≤t<20 s; 乘性故障([0.6, 0;0, 0.1]), 20 s≤t<30 s; 右副翼卡死在15°位置, 30 s≤t≤40 s。混合故障2为10 s≤t≤25 s时, 加性故障和乘性故障同时发生(2+sin0.2t, 0.4), 输出曲线如图 7和图 8所示。同上只列出混合故障1时的曲线。从图 7~9可以看出, 容错控制器在混合故障情况下能保持控制量一致有界, 输出曲线快速跟踪参考信号, 超调和误差均较小, 具有较强的鲁棒性和容错性。图 10至图 12的仿真结果表明, 参数估计值被限制在设计范围内, 保持一致稳定有界。
 |
图 1 无故障时输出曲线 |
 |
图 2 单一故障模式下的输出曲线 |
 |
图 3 故障1时L1自适应容错控制器控制信号 |
 |
图 4 故障1时 |
 |
图 5 故障1时 |
 |
图 6 故障1时 |
 |
图 7 混合故障1模式下的输出曲线 |
 |
图 8 混合故障2模式下的输出曲线 |
 |
图 9 混合故障1时L1自适应容错控制器的控制信号 |
 |
图 10 混合故障1时 |
 |
图 11 混合故障1时 |
 |
图 12 混合故障1时 |
5 结论
飞行器是强耦合、强非线性的不确定性系统, 执行器故障加剧了系统不确定性的影响。本文针对飞行器横侧向控制中执行器故障引起的匹配/非匹配不确定性, 设计L1自适应容错控制器, 克服了自适应控制中不期望的高频振荡和执行器故障引起的不确定性, 实现了闭环系统的快速自适应和鲁棒性。
References
- CHENG Yixin, XU Bin, WU Feng, et al. HOSM Observer Based Robust Adaptive Hypersonic Flight Control Using Composite Learning[J]. Neurocomputing, 2018, 29598–107 [Article] [CrossRef] [Google Scholar]
- WANG Ban, ZHANG Youmin. An Adaptive Fault-Tolerant Sliding Mode Control Allocation Scheme for Multirotor Helicopter Subject to Simultaneous Actuator Faults[J]. IEEE Trans on Industrial Electronics, 2017, 65(5): 4227–4236 [Article] [Google Scholar]
- CAO Chengyu, HOVAKIMYAN N. Design and Analysis of a Novel L1 Adaptive Controller, Part Ⅰ: Control Signal and Asymptotic Stability[C]//Proceedings of the 2006 American Control Conference Piscataway, 2006: 3397–3402 [Google Scholar]
- CAO Chengyu, HOVAKIMYAN N. Design and Analysis of a Novel L1 Adaptive Controller, PartⅡ: Guaranteed Transient Performance[C]//Proceedings of the 2006 American Control Conference Piscataway, 2006: 3403–3408 [Google Scholar]
- ZUO Zongyu, RU Pengkai. Augmented L1 Adaptive Tracking Control of Quad-Rotor Unmanned Aircrafts[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50(4): 3090–3101 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- ZUO Zongyu, MALLIKARJUNAN S. L1 Adaptive Backstepping for Robust Trajectory Tracking of UAVs[J]. IEEE Trans on Industrial Electronics, 2017, 64(4): 2944–2954 [Article] [CrossRef] [Google Scholar]
- LIU Xiaoxiong, XU Heng, WANG Liangliang, et al. L1 Adaptive Configuration Control for Aircraft Control Surface Failure[J]. Computer Measurement & Control, 2015, 23(10): 3415–3417 [Article] [Google Scholar]
- MA Jun, NI Shihong, XIE Wujie, et al. L1 Fault Tolerant Control for Aircraft Actuator Fault with Matched and Unmatched Uncertaines[J]. Control and Decision, 2017, 32(6): 967–975 [Article] [Google Scholar]
- DURHAM Wc, LUTZE Fh. Perfect Explicit Model-Following Control Solution to Imperfect Model-Following Control Problems[J]. Journal of Guidance, Control, and Dynamic, 1989, 14(2): 391–397 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- CAO Chengyu, HOVAKIMYAN N. L1 Adaptive Controller for a Class of Systems with Unknown Nonlinearities: Part Ⅰ[C]//American Control Conference, 2008: 4093–4098 [Google Scholar]
All Figures
 |
图 1 无故障时输出曲线 |
| In the text | |
 |
图 2 单一故障模式下的输出曲线 |
| In the text | |
 |
图 3 故障1时L1自适应容错控制器控制信号 |
| In the text | |
 |
图 4 故障1时 |
| In the text | |
 |
图 5 故障1时 |
| In the text | |
 |
图 6 故障1时 |
| In the text | |
 |
图 7 混合故障1模式下的输出曲线 |
| In the text | |
 |
图 8 混合故障2模式下的输出曲线 |
| In the text | |
 |
图 9 混合故障1时L1自适应容错控制器的控制信号 |
| In the text | |
 |
图 10 混合故障1时 |
| In the text | |
 |
图 11 混合故障1时 |
| In the text | |
 |
图 12 混合故障1时 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.