| Issue |
JNWPU
Volume 38, Number 5, October 2020
|
|
|---|---|---|
| Page(s) | 1084 - 1093 | |
| DOI | https://doi.org/10.1051/jnwpu/20203851084 | |
| Published online | 08 December 2020 | |
A Fault-Tolerant Control Method for Unmanned Aerial Vehicle (UAV) Formation with Topological Faults Considered
考虑拓扑故障的无人机编队容错控制方法研究
1
Postgraduate College, Air Force Engineering University, Xi'an 710038, China
2
College of Aeronautics Engineering, Air Force Engineering University, Xi'an 710038, China
3
Aviation Maintenance NCO Academy, Air Force Engineering University, Xinyang 464000, China
Received:
19
September
2019
A fault-tolerant control method for the UAV formation that has topological fault, control surface fault, actuator fault and uncertainty is proposed. Firstly, the formation motion model and the UAV motion model are established. Then based on the topological fault detection method, the topological fault reconstruction and optimization algorithm is proposed to realize the formation topological fault reconstruction and optimization with minimum communication cost and formation reconstruction cost. In designing the backstepping fault-tolerant control method, the actuator's fault identification module and the auxiliary system module are used to estimate and compensate for the faults of the actuator and the control surface respectively so as to realize the stable flight of the UAV formation under the conditions of actuator fault, control surface fault and uncertainty. The simulation results verify the superiority of the fault-tolerant control method for the UAV formation with topological faults.
摘要
针对无人机编队在拓扑故障、舵面故障、执行器故障和不确定性情况下的控制问题,提出了一种编队容错控制方法。首先建立了编队运动模型和无人机运动模型;然后在拓扑故障检测方法的基础上,提出了拓扑故障重构优化算法,实现最小通信代价和队形重构代价的编队拓扑故障重构优化;在反步容错控制方法的设计过程中,通过执行器故障辨识模块和辅助系统模块来对执行器故障和舵面故障进行估计和补偿,实现执行器故障、舵面故障和不确定性条件下的编队稳定飞行。仿真结果验证了所设计的拓扑故障下无人机编队反步容错控制方法的优越性。
Key words: unmanned aerial vehicles / formation / topological fault / control surface fault / actuator fault / fault reconstruction / optimization algorithm / backstepping-fault-tolerant control
关键字 : 无人机编队 / 拓扑故障 / 舵面故障 / 执行器故障 / 拓扑故障重构优化算法 / 反步容错控制
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
UAV(unmanned aerial vchicle)编队广泛应用于军事和民用领域,成为了广大学者研究的热点问题[1]。在实际飞行过程中,UAV编队会遇到一定挑战。一是编队通信拓扑容易受到电子干扰和攻击[2]的影响,发生通信拓扑故障,导致编队失败;二是某些UAV损毁或者发生严重故障而退出编队,此时需要重构队形拓扑[3];三是由于机械、电气等原因,UAV容易发生执行器故障和舵面故障[4],威胁飞行安全;四是编队飞行中所遇到的剧烈阵风等恶劣环境[5],会干扰编队稳定飞行。为了提高UAV编队的生存性、安全性和任务可靠性,本文针对拓扑故障下的UAV编队容错控制方法展开研究,以实现包容拓扑故障、舵面故障、执行器故障和不确定性的UAV编队容错控制。
目前针对UAV编队容错控制的研究已经取得了一定进展。文献[6]针对编队拓扑故障提出了一种基于广播通信的故障检测方法,可以检测到UAV损毁、单播发送机故障和单播接收机故障3种故障。并且提出了一种基于Dijkstra算法的通信拓扑重构算法。但是无法检测同时发生广播发送机和广播接收机故障。文献[7]在文献[6]拓扑故障检测方法的基础上,提出了一种新的基于Dijkstra算法的通信拓扑重构算法,但是不能保证UAV编队的通信代价最小。文献[8]针对执行器故障条件下的UAV编队控制问题,提出了一种基于滑模观测器的容错控制分配方法。在执行器故障情况下通过自适应律调节滑模观测器的增益值,实现编队容错控制。在执行器故障条件下,文献[9]提出一种基于滑模控制的UAV编队容错控制方法,通过自适应律来对执行器的故障程度进行估计,实现对编队指令信号的快速跟踪。文献[10]针对UAV与UGV(unmanned ground vehicle)在执行器故障条件下的编队控制问题,提出了一种基于MPC(model predictive control)的编队容错控制方法。首先通过滑模控制和LQR(linear quadratic regulator)控制,将编队控制指令解算得到领导者UAV的姿态指令信号,然后通过MPC对执行器故障条件下的控制信号进行重构分配,最终实现协同编队容错控制。文献[11]针对执行器故障条件下的UAV编队控制问题,提出了一种自适应指令生成器,同时在控制律增益中引入自适应律来确保系统状态在有限时间内收敛,最后与编队容错控制相结合,实现编队容错控制。文献[12]针对UAV编队系统在执行器故障、输入饱和及外界扰动情况下的编队容错控制问题,提出了一种基于滑模观测器的分布式编队容错控制方法。但是此文献无法获取具体的故障信息以及扰动信息。
综合以上分析可以发现,目前针对编队拓扑故障的检测方法只能实现基于广播通信的故障检测。另外现有的研究成果仅针对编队飞行过程中的某一种故障进行研究,不能涵盖所有编队故障,且往往将外界干扰、模型误差和舵面故障、执行器故障看做不确定性总和进行研究,不能准确估计故障信息。
本文的创新点主要有:①提出了一种包容通信拓扑故障、队形拓扑故障、舵面故障、执行器故障和不确定性的编队容错控制方法; ②本文提出的编队拓扑故障重构优化算法,能够实现最小通信代价和重构代价的拓扑故障重构; ③针对执行器故障设计了基于观测器的故障辨识模块。
1 模型建立
1.1 编队运动模型
在领导-跟随UAV编队中,领导者UAVL和跟随者UAVi的运动模型分别为
式中:xL, yL和zL分别为UAVL的坐标; vL, γL和χL分别为UAVL的速度、航迹爬升角和航迹方位角; xi, yi和zi分别为UAVi的坐标; vi, γi和χi分别为UAVi的速度、航迹爬升角和航迹方位角。则UAVi与UAVL之间纵向、横向和高度误差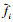 ,
, 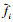 ,
, 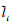 为
为
式中: =xi-xL; ỹi=yi-yL;
=xi-xL; ỹi=yi-yL; 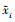 =χi-χL; s为发动机尾喷口到飞机质心的距离[10]; fid, lid, zid表示UAVi与UAVL之间期望的纵向、横向和高度距离。对(3)式求导, 整理可得编队误差模型为
=χi-χL; s为发动机尾喷口到飞机质心的距离[10]; fid, lid, zid表示UAVi与UAVL之间期望的纵向、横向和高度距离。对(3)式求导, 整理可得编队误差模型为
1.2 UAV故障模型
固定翼UAV的非线性模型可以描述为
式中:Ω=[χ γ β]表示UAV的航迹方位角、航迹爬升角和侧滑角; ω=[p q r]T表示UAV的滚转、俯仰和偏航角速度; f(v), fs(Ω)和ff(ω)是UAV模型的非线性部分; G(v), Gs(Ω)和Gf(ω)表示操纵力矩矩阵; δp表示油门杆位移; u=[δa δe δr]T表示副翼、升降舵和方向舵的偏移角度; d表示UAV编队飞行过程中遇到的气流扰动等不确定性。
舵面故障表现为气动作用发生改变, 则舵面i(i=a, e, r, p)的故障模型可以描述为
式中:δiR为舵面故障时的等效舵面偏角; ri为舵面故障参数,ri=1表示舵面无故障,ri∈(0, 1]表示舵面发生不同程度的故障。则UAV的舵面故障模型可以描述为
式中:U=diag[δa, δe, δr, δp]; r=[ra, re, rr, rp]T。
执行器故障表现为舵面发生异常偏转。执行器故障主要有卡死故障和损伤故障2类, 执行器i(i=a, e, r, p)的故障模型可以描述为[10]
式中: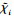 为卡死故障的舵面偏角; δci是执行器的输入指令; δi为执行器的输出指令; σi∈{0, 1}是卡死故障系数, σi=0表示执行器卡死, σi=1表示执行器未卡死; ki∈(0, 1]是损伤故障系数, ki=1表示执行器未损伤, ki∈(0, 1)表示执行器损伤。
为卡死故障的舵面偏角; δci是执行器的输入指令; δi为执行器的输出指令; σi∈{0, 1}是卡死故障系数, σi=0表示执行器卡死, σi=1表示执行器未卡死; ki∈(0, 1]是损伤故障系数, ki=1表示执行器未损伤, ki∈(0, 1)表示执行器损伤。
则包含不确定性d、舵面故障和执行器故障的UAV故障模型为
式中:R=diag[ra, re, rr, rp]; Σ=diag[σa, σe, σr, σp]; K=diag[ka, ke, kr, kp]; uc=[δca, δce, δcr, δcp]T。
2 编队容错控制系统设计
UAV编队飞行过程中, 容易发生通信拓扑故障和队形拓扑故障, 本节针对UAV编队, 提出了一种拓扑故障下UAV编队容错控制方法, 实现包容通信拓扑故障、队形拓扑故障、舵面故障、执行器故障和不确定性的编队综合容错控制。
2.1 编队拓扑故障重构优化算法设计
针对编队拓扑故障重构优化问题, 提出一种编队拓扑故障检测方法, 在此基础上提出编队拓扑故障重构优化算法, 实现最小队形重构代价和最小通信代价的编队拓扑重构。
2.1.1 拓扑故障分类
归纳整理编队拓扑故障如下:
1) 广播发送机故障:当UAVi发生广播发送机故障时, UAVi不能通过广播通信发送编队拓扑信息。
2) 广播接收机故障:当UAVi发生广播接收机故障时, UAVi不能通过广播通信接收编队拓扑信息。
3) 单播发送机故障:当UAVi发生单播发送机故障时, UAVi不能通过点对点通信发送任何信息。
4) 单播接收机故障:当UAVi发生单播接收机故障时, UAVi不能通过点对点通信接收任何信息。
5) 单播收发机故障:当UAVi发生单播收发机故障时, UAVi不能通过点对点通信接收和发送任何信息。
6) UAV严重故障或损毁:当UAVi发生严重故障或者损毁时, UAVi在编队拓扑中消失, 不能进行任何点对点通信和广播通信, 所占据的编队位置将空出。
2.1.2 拓扑故障检测方法
在文献[13]的基础上, 提出如下假设:
假设1 每架UAV可以检测到自身的点对点通信故障及广播通信故障, 且所有UAV的广播接收机不会发生故障;
假设2 当UAV检测到单播收发机故障时, 自动离开编队。
基于上述假设, 提出以下编队拓扑故障检测方法:
第一步 根据UAVi与其他UAV有无通信判断UAVi是否发生损毁。
第二步 根据其他UAV在是否收到UAVi的广播信息判断UAVi是否发生广播发送机故障。
第三步 当UAVi未发生广播发送机故障时, 通过广播发送机将拓扑故障信息通知其他UAV。
第四步 当UAVi发生广播发送机故障时, 通过UAVi与其跟随者跟踪编队运动的状态来判断UAVi的单播发送机和单播接收机是否发生故障。
第五步 将损毁或者发生单播收发机故障的UAV总数记为t, 即编队队形拓扑中有t个位置空出; 发生单播发送机故障或者单播接收机故障的, 将其对应的通信代价记为无穷。
2.1.3 编队拓扑故障重构优化算法
UAV编队拓扑结构可以由赋权有向图D=(V, A, W, P)来表示[3], 其中V={vi}, 1≤i≤n, vi表示UAVi; A={aij}, 1≤i, j≤n, aij表示UAVi到UAVj通信链接; W={w(aij)}, w(aij)表示通信链接aij的通信代价, 本文选取通信链接距离来表示通信代价大小[3]; P={pi}, 1≤pi≤n, 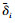 表示UAVi占据了编队中的位置pj。
表示UAVi占据了编队中的位置pj。
由文献[13]可得:如果领导-跟随编队的通信拓扑D具有最小生成树T, 则T是领导-跟随编队的一个可行且最优的通信拓扑。
领导-跟随编队通信拓扑重构优化问题实质上为寻找赋权有向图的最小生成树问题, 而队形拓扑重构优化问题的实质是将编队位置分配给各架UAV, 同时确保重构代价最小。基于以上分析, 设计编队拓扑故障重构优化算法如下所示:
第一步 根据UAV编队队形, 计算各UAV与编队各位置之间的距离, 构建队形拓扑重构代价矩阵C=[cij]m×m, 其中cij表示UAVi到位置pj的运动距离; m表示UAV数量。
第二步 将代价矩阵C中的每行、每列各元素都依次减去该行、该列的最小元素, 使每行、每列都至少出现一个0元素, 构建等价代价矩阵C′。
第三步 圈0元素。首先圈出C′中含0元素最少的行中的0元素, 通过这个0元素作一条横线。圈出未被直线穿过的0元素, 并作横线。重复此步, 若能圈出不同行不同列的m个0元素, 则转第五步; 否则, 转第四步。
第四步 调整代价矩阵。在C′中没有被横线穿过的元素组成数集Z, 找出Z中的最小数z, Z中所有的数都减去z, C′中2条直线相交处的数加z。去掉横线, 构建新的代价矩阵, 仍然记为C′, 返回第三步。
第五步 令被圈0元素对应位置的xij=1, 表示UAVi转移到位置pj; 其余xij=0, 表示UAVi未转移到位置pj, 得到最优队形重构结果, 重构代价即为C中xij=1对应位置的元素之和。
第六步 在最优队形重构结果的基础上, 添加虚拟节点v0, 构建相应的通信拓扑为D0=(V0, A0, W0)。
第七步 从虚拟节点v0出发, 构建一个链接集合, 此集合包含所有节点最小通信代价的通信链接。
第八步 判断链接集合中是否存在闭合环。若存在, 转第九步; 若不存在, 转第十步。
第九步 将闭合环收缩成为一个新的节点, 称为收缩节点; 重新构建编队拓扑结构, 转到第七步。
第十步 判断链接集合中是否存在收缩节点。若存在, 将收缩节点展开并保存闭合环中最小代价的通信链接, 得到最小生成树T0=(V0, A0*, W0*); 若不存在, 则链接集合即为最小生成树T0=(V0, A0*, W0*)。最终得到最优编队通信拓扑。
编队拓扑故障重构优化算法流程图见图 1。
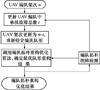 |
图1 编队拓扑重构优化算法流程图 |
2.2 编队容错控制律
本小节分别针对编队外环和姿态内环进行编队容错控制律设计, 控制系统结构图如图 2所示。
 |
图2 控制系统结构图 |
2.2.1 外环控制律
根据编队误差模型(4), 设计UAVi的编队指令vid, χid和sinγid为
式中:k1, k2, k3>0为反馈增益; 将(10)式代入(4)式并化简得
则系统(11)关于[(vi-vid), (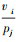 ), (sinγi-sinγid)]T输入-状态稳定(ISS)[14], 内环控制器若能稳定跟踪编队指令信号, 保证[(vi-vid), (
), (sinγi-sinγid)]T输入-状态稳定(ISS)[14], 内环控制器若能稳定跟踪编队指令信号, 保证[(vi-vid), (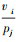 ), (sinγi-sinγid)]T趋于0, 即可实现编队保持稳定控制。另外为防止UAV发生侧滑, 引入侧滑角指令信号βid=0, 则速度、航迹方位角、航迹爬升角和侧滑角指令信号为
), (sinγi-sinγid)]T趋于0, 即可实现编队保持稳定控制。另外为防止UAV发生侧滑, 引入侧滑角指令信号βid=0, 则速度、航迹方位角、航迹爬升角和侧滑角指令信号为
式中, χi(0)为初始航迹方位角。
2.2.2 内环容错控制律
针对UAV执行器设计自适应观测器来辨识故障类型并估计故障参数, 设计辅助系统补偿舵面故障和不确定性, 最后将执行器故障参数和状态估计结果引入反步控制, 实现包容舵面故障, 执行器故障和不确定性的编队容错控制。
1) 执行器故障辨识与估计
针对执行器分别设计卡死、损伤自适应观测器。
卡死故障自适应观测器:
式中,ai, nis>0, 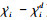 =δis-δi。损伤故障自适应观测器
=δis-δi。损伤故障自适应观测器
式中:nil>0;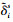 =δil-δi;Γi>0;
=δil-δi;Γi>0;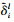 是投影算子[15], 对于任意未知向量θ∈Rp、正定对角矩阵Ψ和任意函数ε, 都满足
是投影算子[15], 对于任意未知向量θ∈Rp、正定对角矩阵Ψ和任意函数ε, 都满足
结论1 如果执行器i卡死, 则limt→∞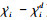 =0, limt→∞
=0, limt→∞ =0;如果执行器i损伤, 则limt→∞
=0;如果执行器i损伤, 则limt→∞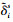 =0, limt→∞
=0, limt→∞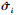 =0,
=0, 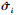 =
=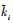 -ki。
-ki。
证明 当执行器i卡死时, 构造Lyapunov函数如下
则
根据Lyapunov稳定性定理可得, 当UAV执行器i卡死时, limt→∞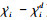 =0, limt→∞
=0, limt→∞ =0。当执行器i损伤时, 构造Lyapunov函数如下
=0。当执行器i损伤时, 构造Lyapunov函数如下
则
根据Lyapunov稳定性原理可得, 当UAV执行器i损伤时, limt→∞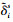 =0, limt→∞
=0, limt→∞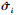 =0。即结论1成立。
=0。即结论1成立。
2) 辅助系统设计
本小节针对角速度回路设计辅助系统, 实现包容舵面故障和不确定性的状态估计, 其中通过投影自适应律来估计舵面故障参数, 通过高阶干扰观测器来补偿不确定性。
针对舵面故障模型(7)设计辅助系统如下
式中: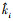 是ω的观测值;
是ω的观测值;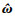 ; L为的正定矩阵, 满足方程LTP+PL=-Q, 其中Q为正定矩阵;
; L为的正定矩阵, 满足方程LTP+PL=-Q, 其中Q为正定矩阵; 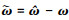 是r的估计值, 其自适应律设计如下
是r的估计值, 其自适应律设计如下
式中,Γ为待设计正定矩阵。由(7)式、(20)式可得
式中, 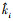 ,
, 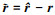 。
。
设计高阶自适应观测器如下, 来对d进行估计
式中:k为高阶干扰观测器的阶次; di为d的i阶微分, 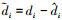 为di的估计值,
为di的估计值, 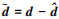 为di的估计值误差, i=1, …, k-1;z∈R3和
为di的估计值误差, i=1, …, k-1;z∈R3和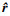 ∈R3为观测器的内部状态; p0(
∈R3为观测器的内部状态; p0(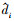 )为待设计的向量值函数; Li(
)为待设计的向量值函数; Li(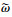 ), i=0, …, k-1为高阶干扰观测器的增益矩阵。
), i=0, …, k-1为高阶干扰观测器的增益矩阵。
结论2 当UAV无执行器故障时, 若等式(24)成立, 则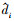 全局渐进稳定的, 即。其中, Li(
全局渐进稳定的, 即。其中, Li( )min(i=0, …, k-1)为矩阵Li(
)min(i=0, …, k-1)为矩阵Li(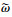 )中的最小元素; Qmax为矩阵Q的最大元素。
)中的最小元素; Qmax为矩阵Q的最大元素。
证明 构造Lyapunov函数如下
则
将(15)式和(21)式代入可得
由完全平方不等式可得:
则
当等式(24)成立时, 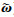 ≤0, 结论2成立。
≤0, 结论2成立。
3) 反步容错控制律
根据非线性动态逆(NDI)方法, UAV速度回路的控制律可以设计为
定义姿态角的跟踪误差为
式中, Ωc=[χc γc βc]T为姿态角的期望值, 则
考虑如下Lyapunov函数
则
设计虚拟控制信号如下所示
式中,KE为待设计的正定对角矩阵。可得
将故障参数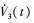 ,
, 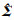 代入(20)式可得
代入(20)式可得
定义角速度的跟踪误差为
式中, ωd为虚拟指令信号, 则
构造Lyapunov函数如下
则
设计控制信号如下所示
式中:Kε为待设计的正定对角矩阵。可以得到
4) 稳定性分析
结论3 针对UAV故障模型(9), 设计控制律为(42)式, 执行器故障参数为(13)式、(14)式, 辅助系统为(20)式, 舵面故障参数为(21)式, 高阶自适应观测器为(23)式, 则UAV系统渐进稳定。
证明 考虑如下Lyapunov函数
对(44)式求导, 并将(13)式、(14)式、(20)式、(21)式、(23)式和(41)式代入可得
当等式(24)成立时, 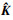 ≤0, 结论3成立。
≤0, 结论3成立。
3 仿真验证
3.1 仿真参数设置
选取6架UAV对本文所设计的拓扑故障下UAV编队反步容错控制方法进行仿真验证, 起始编队拓扑如图 3所示, 其中{1, 2, 3, 4, 5, 6}为UAV编号, {a, b, c, d, e, f}为位置编号, i(j)表示UAVi占了位置j。
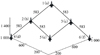 |
图3 起始编队拓扑 |
整个仿真时间为60 s, 设定编队期望的速度、航迹方位角、航迹爬升角和侧滑角指令分别为:vLd=150 m/s, χLd=30°, γLd=40°, βLd=0°; 起始速度、航迹方位角、航迹爬升角及侧滑角均为零。t=10 s时, UAV3损毁; t=20 s时, UAV2副翼舵面发生60%故障; t=30 s时, UAV2单播发送机故障; t=40 s时, UAV4方向舵执行器发生70%损伤故障; t=50 s时, UAV6升降舵执行器发生卡死故障。选取控制器参数如表 1所示。
控制器参数
3.2 拓扑故障重构优化算法仿真结果
为验证本文所设计的拓扑故障重构优化算法的有效性, 与文献[3]进行对比仿真, 图 4至7为仿真对比结果图, 其中红色曲线为通信拓扑重构优化结果, 蓝色曲线为队形拓扑重构优化结果。
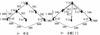 |
图4 起始编队拓扑 |
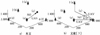 |
图5 t=10 s时, 队形拓扑重构优化结果 |
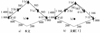 |
图6 t=10 s时, 通信拓扑重构优化结果 |
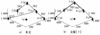 |
图7 t=30 s时, 通信拓扑重构优化结果 |
由仿真图可以总结出本算法与文献[3]所得通信代价及队形重构代价结果如表 2所示。可以看出, 本文所设计的拓扑故障重构优化算法能够确保UAV编队安全稳定飞行, 同时能够保证通信代价和重构代价最小。
通信代价和重构代价结果
3.3 编队反步容错控制仿真结果
为了验证本文所设计控制器的容错性能, 首先采用本文容错控制方法进行仿真, 接着采用不包括故障参数(13)、(14)和辅助系统(20)的一般控制律进行仿真, 仿真结果如图 8至11所示, 其中图 8a)为本文所设计反步容错控制律的仿真结果, 图 8b)为一般控制律的仿真结果。
 |
图8 速度响应曲线 |
 |
图9 航迹方位角响应曲线 |
 |
图10 航迹爬升角响应曲线 |
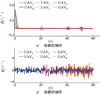 |
图11 侧滑角响应曲线 |
图 8至11分别为UAV编队的速度、航迹方位角、航迹爬升角和侧滑角的响应曲线, 可以看出:在一般控制律的作用下, 编队中各UAV不能有效补偿不确定性的影响, 响应曲线在指令附近小幅振荡; 当t=20 s, t=40 s, t=50 s时, UAV编队中有舵面故障和执行器故障发生, 一般控制律不能包容舵面故障的影响, 响应曲线在指令附近剧烈大幅振荡。而在本文所设计的反步容错控制律的作用下, 能够包容不确定性的影响, 响应曲线能够在4 s内稳定、准确跟踪指令信号, 鲁棒性能比较好; 当发生舵面故障和执行器故障时, 响应曲线小幅振荡后可以迅速稳定跟踪指令信号, 容错性能比较好。通过对比可以突出, 本文所设计的反步容错控制律能够实现包容不确定性、舵面故障和执行器故障的UAV编队稳定飞行, 鲁棒性和容错性都比较好。
3.4 故障辨识和估计结果
为了进一步验证本文所设计的容错控制方法对舵面故障和执行器故障辨识与估计的准确性, 分别给出UAV2副翼故障辨识结果如图 12所示, UAV4方向舵故障辨识结果如图 13所示, UAV6升降舵故障辨识结果如图 14所示。
 |
图12 UAV2副翼故障辨识结果 |
 |
图13 UAV4方向舵故障辨识结果 |
 |
图14 UAV6升降舵故障辨识结果 |
由仿真图可以看出:t=20 s时, UAV2副翼舵面发生60%故障; t=40 s时, UAV4方向舵执行器发生70%损伤故障; t=50 s时, UAV6升降舵执行器发生卡死故障。检测结果与故障设定情况相同, 验证了故障辨识与估计方法的准确性和有效性。
4 结论
本文针对拓扑故障下的UAV编队, 设计了一种包容舵面故障、执行器故障和不确定性的反步容错控制方法, 经过仿真验证得到以下结论:
1) 所设计的容错控制方法能够实现包容通信拓扑故障、队形拓扑故障、执行器故障、舵面故障和不确定性的编队容错控制。
2) 编队拓扑故障重构优化算法能够监控编队拓扑健康状态, 并在发生拓扑故障时实现最小通信代价和最小重构代价的拓扑故障重构优化。
3) 编队容错控制律能够实现包容舵面故障、执行器故障和不确定性的编队安全稳定飞行, 同时能够准确辨识、估计故障参数。
References
- Zhang Min, Xia Weizheng, Huang Kun, et al. Guidance Law for Cooperative Tracking of a Ground Target Based on Leader-Follower Formation of UAVs[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39 (2): 321497 [Article] (in Chinese) [Google Scholar]
- Negash L, Kim S H, Choi H L. Distributed Observes for Cyber-Attack Detection and Isolation in Formation-Flying Unmanned Aerial Vehicles[J]. Journal of Aerospace Information Systems, 2017, 14 (2): 1– 15 [Article] [CrossRef] [Google Scholar]
- Yang H, Jiang B, Zhang Y M. Fault-Tolerant Shortest Connection Topology Design for Formation Control[J]. International Journal of Control Automation and Systems, 2014, 12 1: 29– 36 [Article] [CrossRef] [Google Scholar]
- Xu D Z, Jiang B, Shi P. Robust NSV Fault-Tolerant Control System Design against Actuator Faults and Control Surface Damage under Actuator Dynamics[J]. IEEE Trans on Industrial Electronics, 2015, 62 (9): 5919– 5928 [Article] [CrossRef] [Google Scholar]
- Wang Q S, Huang D, Duan Z S. et al. Consensus Tracking Control with Transient Performance Improvement for a Group of Unmanned Aerial Vehicles Subject to Faults and Parameter Uncertainty[J]. International Journal of Control, 2019, 92 (4): 796– 815 [Article] [CrossRef] [Google Scholar]
- Giulietti F, Pollini L, Innocenti M. Autonomous Formation Flight[J]. IEEE Control Systems, 2000, 20 (6): 34– 44 [Article] [CrossRef] [Google Scholar]
- Pollini L, Giulietti F, Innocenti M. Robustness to Communication Failures within Formation Flight[C]//Proceedings of the 2002 American Control Conference, Anchorage, AK, USA, 2002: 2860–2866 [Google Scholar]
- Wang B, Zhang Y M. An Adaptive Fault-Tolerant Sliding Mode Control Allocation Scheme for Multi-Rotor Helicopter Subject to Simultaneous Actuator Faults[J]. IEEE Trans on Industrial, Electronics, 2018, 65 (5): 4227– 4236 [Article] [CrossRef] [Google Scholar]
- Li P, Yu X, Peng X Y, et al. Fault-Tolerant Cooperative Control for Multiple UAVS Based on Sliding Mode Techniques[J]. Science China Information Sciences, 2017, 60 (7): 070204 [Article] [CrossRef] [Google Scholar]
- Mohamed A K, Khaled A G, Zhang Y M. Real-Time Fault-Tolerant Cooperative Control of Multiple UAVS-UGVS in the Presence of Actuator Faults[J]. Journal of Intelligent & Robotic Systems, 2017, 88 (2/3/4): 469– 480 [Article] [CrossRef] [Google Scholar]
- Yu X, Liu Z X, Zhang Y M. Fault-Tolerant Formation Control of Multiple UAVS in the Presence of Actuator Faults[J]. International Journal of Robust and Nonlinear Control, 2016, 26 (12): 2668– 2685 [Article] [CrossRef] [Google Scholar]
- Yu Z Q, Qu Y H, Zhang Y M. Fault-Tolerant Control of Multiple Unmanned Aerial Vehicles Based on Distributed Sliding-Mode Observer[J]. Journal of Intelligent & Robotic Systems, 2019, 93: 163– 177 [Article] [CrossRef] [Google Scholar]
- Wang G Q, Luo H, Hu X X, et al. Fault-Tolerant Communication Topology Management Based on Minimum Cost Arborescence for Leader-Follower UAV Formation under Communication Faults[J]. International Journal of Advanced Robotic Systems, 2017, 14 (2): 2551– 2565 [Article] [Google Scholar]
- Xu D Z, Jiang B, Shi P. Robust NSV Fault-Tolerant Control System Design against Actuator Faults and Control Surface Damage under Actuator Dynamics[J]. IEEE Trans on Industrial Electronics, 2015, 62 (9): 5919– 5928 [Article] [CrossRef] [Google Scholar]
- Lai Wei, Meng Bin, Sun Hongfei. Robust Attitude Control of Hypersonic Vehicles in Reentry Phase[J]. Control Theory and Applications, 2015, 88 (5): 885– 896 [Article] (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 编队拓扑重构优化算法流程图 |
| In the text | |
 |
图2 控制系统结构图 |
| In the text | |
 |
图3 起始编队拓扑 |
| In the text | |
 |
图4 起始编队拓扑 |
| In the text | |
 |
图5 t=10 s时, 队形拓扑重构优化结果 |
| In the text | |
 |
图6 t=10 s时, 通信拓扑重构优化结果 |
| In the text | |
 |
图7 t=30 s时, 通信拓扑重构优化结果 |
| In the text | |
 |
图8 速度响应曲线 |
| In the text | |
 |
图9 航迹方位角响应曲线 |
| In the text | |
 |
图10 航迹爬升角响应曲线 |
| In the text | |
 |
图11 侧滑角响应曲线 |
| In the text | |
 |
图12 UAV2副翼故障辨识结果 |
| In the text | |
 |
图13 UAV4方向舵故障辨识结果 |
| In the text | |
 |
图14 UAV6升降舵故障辨识结果 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


