EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 42 / No 4 (August 2024) JNWPU, 42 4 (2024) 652-661 Full HTML
Open Access
Issue
JNWPU
Volume 42, Number 4, August 2024
Page(s) 652 - 661
DOI https://doi.org/10.1051/jnwpu/20244240652
Published online 08 October 2024

© 2024 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

随着大功率、高功重比电机技术的发展, 电动伺服舵机(或称为机电作动器)逐步成为新型作动技术的发展前沿, 它摈弃了传统液压伺服舵机对集中能源的使用方式, 而采用高压电源的能源方式，具备典型的分布式特征, 在可靠性、维修性及复杂性等方面具有明显优势[1–3], 目前已成为中低功率和输出力作动技术的代表。

而随着电动伺服舵机在汽车控制、飞机飞行控制和发动机控制等安全关键系统中的应用越来越广泛[4–6], 不仅在伺服闭环控制精度方面的要求越来越高, 即要求其采用高速电机、高精密传动机构减小机械传动间隙, 并配置合理的位置反馈传感器和速度反馈传感器实现闭环控制; 而且对整个伺服控制回路的容错能力要求也越来越严苛。受限于电机、机械齿轮等在体积、质量方面的限制, 以及在基本可靠性提升方面的约束, 往往在电气方面采用多余度配置方式提升整体伺服控制的容错能力[7–9], 使电动伺服舵机具备较高的安全性和任务可靠性, 如采用主/备两余度的线圈实现对电机控制的感应、采用多余度的位置传感器实现对反馈信号的采集。这就要求电动伺服舵机具备完整的故障检测、定位和隔离机制, 以确保服控制回路的容错能力[10–16]。

面向安全关键系统传感器最为常见的故障诊断方法是以多余度比较为主的故障检测和定位策略。这种策略通过多个余度间传感器信息的比较来识别故障余度的传感器[17–22], 并且具有跨余度间比较、跨表决值比较等多种有效方法。随着研究应用的不断深入, 研究人员发现基于多余度比较的故障诊断方法能够有效处理传感器机械卡死、存在恒定偏差、电气通道短路等故障模式, 能够在超过设计阈值时进行精准识别。但是, 在面临2∶2, 1∶1∶1, 1∶1等奇异故障模式时, 基于多余度比较的方法将完全失效，无法识别故障余度, 进而给闭环控制带来较大影响, 甚至引发电动伺服舵机的控制失效, 进一步导致安全关键系统的运行紊乱。

本文在多余度比较的故障诊断方法基础上, 提出基于解析模型的滑动数据窗假设检验方法, 针对传感器的奇异故障模式进行故障诊断策略研究和算法设计, 并以航空机载系统的电动伺服舵机应用为背景, 证明其对控制回路的高精度闭环和高容错控制效果。

1 多余度电动伺服控制

电动伺服舵机通常采用多余度伺服指令级和功率放大级的控制结构。伺服指令级由电机实现电信号驱动指令到电机转速的转换, 以进行功率传输和驱动传递, 且一般采用主/备线圈驱动的多余度电气工作模式。考虑到功率放大以及输出机构传动比的要求, 在电机和输出机构之间存在多级的机械传动机构。为了实现高精度的闭环控制, 在输出机构上配置有多余度位置传感器, 由此可以实现典型的PID闭环控制, 如图 1所示。

作为控制回路的信息反馈级, 当位置传感器的某个余度发生故障时, 可以采用以上所述的基于多余度比较的故障诊断方法, 即通过多个余度的位置传感器信息互相比较来识别故障, 并隔离故障余度的位置传感器, 将剩余正常余度的传感器表决后反馈进入控制回路。

如前所述, 对于位置传感器发生某个余度的机械卡死、恒定偏差等故障模式, 当超过设计阈值时, 可以通过多余度比较方法进行故障检测和识别, 但奇异故障模式的故障检测和识别一直是多余度比较方法难以处理的问题之一。如果不加以解决, 伺服控制失效将可能导致整个系统控制回路的整体失效, 带来灾难性损失。

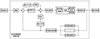thumbnail 图1

电动伺服舵机控制回路框图

2 基于霍尔传感器的故障诊断研究

对于一般的机载系统传感器而言, 当发生2∶2等奇异故障模式时, 可以基于多余度比较的方法定位为“所有余度的传感器都故障”。但是, 作为涉及飞行安全关键功能的传感器, 如飞控系统、发控系统等, 其传感器信号失效可能带来整体控制失效, 比如, 飞控舵面极偏带来瞬态大机动、发动机加力状态下无法降落等情形, 因此，必须尽最大可能避免奇异故障模式。

此时, 单独依靠增加位置传感器的物理余度配置, 无法完全避免奇异故障模式发生, 通过基于模型的解析余度方案[23–24], 利用非相似余度的思想, 寻找到真正的故障传感器, 是解决奇异情形故障诊断问题的合理措施。

基于解析模型的非相似余度信号, 可以分别计算多个/多组奇异信号与解析模型之间的差值, 将超出预先设定阈值范围的一个/一组信号判定为故障信号。如图 2所示, 2个测量信号分别为x1和x2, 当两者的差值超过阈值范围、出现奇异故障情形时, 通过引入解析模型的参考信号xm, 分别形成残差信号r1和r2, 通过对残差进行统计检验, 可以实现奇异故障情形下的故障检测和隔离, 进而达到故障诊断的目的。

考虑到像飞控系统、发控系统等这种高动态强实时机载系统, 其输入输出数据都是不断更新的, 采用某一拍的测量信号(单样本检验)进行故障诊断往往会失真。并且, 其测量信号、解析余度信号都是不断更新, 可能受到模型不确定性等因素影响, 采用固定的测量信号不能反映动态数据更新的特点, 采用滑动数据窗的统计方法就显得非常必要。

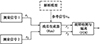thumbnail 图2

奇异故障时引入解析模型的故障诊断框图

2.1 基于滑动数据窗的假设检验方法

采用滑动数据窗的方法, 一方面需要考虑阈值的设计, 当阈值设置较低时, 误报概率会增大, 当阈值设置较高时, 无法实现真实存在的、较小幅值故障的正确隔离; 另一方面需要考虑滑动数据窗的宽度, 也就是所选测量信号的长度, 当宽度较小时, 可能起不到动态采集的作用, 进而影响故障诊断性能(如误报率和虚警率), 当宽度较大时, 会给系统增加较大的算法复杂度和存储空间需求。

定义1  二元假设检验, 是指某个待检测系统的状态有2种假设H1和H2, 根据(0, T)时间内的观测量x(t)来判决假设H1为真或者假设H2为真, 其中, H1表示该系统为正常状态, H2表示该系统为故障状态。

由此可得:

1) 当H1为真, 而判断H2为真时, 称为虚警, 即没有故障的情况下判决为有故障, 其发生的概率为虚警率, 记为Pf;

2) 当H2为真, 而判断H1为真时, 称为漏报, 即有故障的情况下判决为没有故障, 其发生的概率为漏报率, 记为Pm。

具体而言, 将观测量x构成的观测空间划分为2个互不相交的子空间X1和X2, 当观测值x∈X1时, 则判断假设H1为真; 当观测值x∈X2时, 则判断假设H2为真。

设观测值x在假设H1为真或者假设H2为真时的条件概率密度分别为P(x|H1)和P(x|H2), 可得

可以发现, 虚警率Pf和漏报率Pm分别与正确判决概率Pc、故障检测率Pd互补，即

一般情况下, 传感器的检测性能服从正态分布N(μ, σ2), 即

在测量样本容量固定的情况下, 想要减小虚警率Pf, 往往会导致漏报率Pm增大。因此, 在二元假设检验的判决准则中, 要想在实际应用情况下既满足尽量小的虚警率Pf, 也满足尽量小的漏报率Pm, 需要增加测量样本容量, 由此才能达到较好的检测性能, 提升故障检测率。

定义2  滑动数据窗方法, 是指测量信号的数据窗宽度为n, 某一时刻故障检测时选取的数据是从第k-n+1拍到第k拍, 共n个测量信号, 下一时刻选取的数据要减去第k-n+1拍的老数据, 增加第k+1拍的新数据, 即从第k-n+2拍到第k+1拍, 也是n个测量信号, 如图 3所示。

设有独立的正态分布的测量信号序列{xk}, 其方差为σ2, 当测量信号无故障时其均值为0, 属于高斯白噪声过程; 当测量信号故障时其均值为a, 即满足:

当H1为真时, {xk}满足正态分布N(0, σ2);

当H2为真时, {xk}满足正态分布N(a, σ2)。

取其对数似然比, 可得

将对数似然比l(x)正规化为均值为0、方差为1的测量空间变量, 并设

可得y满足:

1) 当H1为真时, yt=;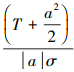

2) 当H2为真时, yt=。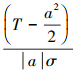

设P(y)是y的概率密度函数, 则其积分分布函数为

于是, 对于单样本检验方法, 可求得其虚警率和漏报率分别为

而对于滑动数据窗方法, n个测量信号: X(k)={x(k-n+1), x(k-n+2), …, x(k)}, 且各个测量信号之间相互独立, 则具有如下的联合概率密度函数:

当H1为真时, {xk}满足正态分布[N(0, σ2)]n;

当H2为真时, {xk}满足正态分布[N(a, σ2)]n。

取其对数似然比, 可得

并满足:

当H1为真时, l(X(k))满足正态分布;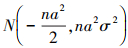

当H2为真时, l(X(k))满足正态分布。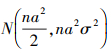

于是, 对于滑动数据窗检验方法, 可求得其虚警率和漏报率分别为

当数据窗口宽度n足够大时, 可以忽略其中的Tn, 可得

同时, 可以求得其极限为

由此可知, 作为一种滑动的多样本检验方法, 当数据窗宽度n足够大时, 滑动数据窗口方法的漏报率和虚警率都将趋于0, 这就将极大提高故障诊断性能。动态系统的测量数据不断更新, 并且是多样本的, 因此滑动数据窗方法要比固定样本检验方法更具优势。但是, 随着数据窗口宽度n的增加, 也将给控制系统提出更高的运算时间需求和测量信号存储需求, 带来更大的故障检测延迟, 这是在飞控、发控这类嵌入式实时系统中应用时必须考虑的问题。下文将讨论如何选取数据窗口宽度n。首先引入定义3[25]。

定义3  OC函数, 是指对参数α的某个检验问题的一种假设检验方法, 对于参数的不同取值均有对应的概率密度函数P(α|H1), 则该概率密度函数被称为参数α的抽样特征函数(即OC函数)。

由此可知, 当α∈H2时, 概率密度函数计算值就是其漏报率Pm, 而1-Pm就是正确的故障检测率。

定理1  对于服从正态分布的测量信号序列{xk}, 在预先规定虚警率为一个定值Pfnd(显著性水平)的基础上, 若将漏报率控制在一个可接受的较小值Pmnd, 可以通过OC函数求得所需滑动数据窗口宽度的大小n, 满足

式中, zPmnd为对应正态分布的分位数。

证明:

设有独立的正态分布的测量信号序列{xk}, 满足:

当H1为真时, 列{xk}满足正态分布N(0, σ2);

当H2为真时, 列{xk}满足正态分布N(a, σ2)。

基于奈曼-皮尔逊准则, 构建统计量

式中, n为滑动数据窗的宽度。由此可知, 有限个相互独立的正态分布测量信号之和仍然服从正态分布, 即:

当H1为真时, Xw满足正态分布N(0, σ2/n);

当H2为真时, Xw满足正态分布N(a, σ2/n)。

考虑测量信号的对称性, 引入双边检验判定规则为

其虚警率计算为

因此, 当给定虚警率要求Pfn≤Pfnd时, 可以计算出对应的阈值T

式中, zPfnd/2为对应正态分布的分位数。

可以看出, 为防止虚警的发生, 阈值T的选取必须大于(22)式所示的数值。残差校验中虚警与漏报发生的原因在于统计量的条件概率分布存在相交部分。当故障发生时的幅值较小时, 相交部分较多, 此时较小的阈值就会导致无故障时虚警概率较大。因此, 选取较大的阈值Tw(Tw=T+τ)可以直接确定故障发生, 即|Xw|≥Tw时, 利用双边检验判断规则判定假设H2成立。

引入OC函数, OC函数中的参数α即为统计量Xw的均值期望。当α>T时, α=a, OC函数的计算值为漏报率Pmn。

当参数α=Tw时, 计算其OC函数的值

考虑到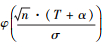趋于1, (24)式进一步略写可得

由于Tw≥T, 可以看出, 当滑动数据窗宽度n越大, 对应的漏报率Pmn(α)会越小, 当给定漏报率要求Pmn≤Pmnd时, 滑动数据窗宽度n需满足

证毕。

thumbnail 图3

滑动数据窗方法的测量信号采集示意图

2.2 基于解析模型的故障诊断算法

结合图 1可知, 电动伺服舵机的位置传感器常采用基于多余度比较的故障诊断方法。同时也可以发现, 为提高伺服闭环可靠性而设置的多余度位置传感器, 由于空间体积和质量受限, 两余度、四余度的电气冗余配置是常见状态, 这就使得传感器可能存在1∶1, 2∶2等奇异故障模式。为解决奇异故障模式下的检测与识别问题, 在基于多余度比较的故障诊断方法基础上, 提出一种基于霍尔传感器模型的故障诊断方法。

电动伺服舵机的核心部分由三相无刷直流电机、减速器等机械传动结构、输出机构及位置传感器组成。在电机中集成对应余度的霍尔传感器可以检测转子位置，进一步实现电机换向。当电机的三相绕组通电产生磁场后, 转子在磁场作用下开始旋转, 而安装在转子上的霍尔传感器将转子的位置信号转变为电信号, 由此可以使得控制器根据设定好的导通顺序以及速度信号的大小来控制逻辑开关的通断顺序和通电时间, 从而改变磁场的大小和方向, 转子受到变化磁场的作用改变运动状态, 如此循环往复完成电机的连续运动。

而电机进行连续转动的前提是按照一定的导通顺序严格进行换相, 霍尔传感器在空间上呈现为120°的布局, 是离散数字信号(以Hall_A、Hall_B、Hall_C来表示), 高电平为信号1, 低电平为信号0。以顺时针转动为例, 接通开关通道顺序依次为V1V6、V1V2、V3V2、V3V4、V5V4、V5V6, 这时霍尔传感器获取到的霍尔信号为准确换相提供依据。因此, 电机旋转1周存在6个不同的霍尔信号状态, 也就是说霍尔信号转变6次即为电机旋转1周, 如表 1所示。

由此可知, 霍尔传感器采集的霍尔信号状态作为电机旋转的表征信号, 其每次状态转变代表了电机正向旋转或者反向旋转的1/6周, 因此可以作为电动旋转角度的解析模型。基于霍尔传感器模型的故障诊断方法具体设计如下。

1) 霍尔传感器的完整自监控设计

作为多余度比较方法的辅助手段, 霍尔传感器自身必须具备完整的自监控能力, 为2∶2等奇异故障下的检测和识别提供可靠的比较对象。

由上文可知, 电机换向的控制必须严格按照霍尔传感器的离散采集信号进行, 对于主/备线圈驱动的电机, 不同的线圈分别配备不同余度的霍尔传感器。当发现某个余度的霍尔传感器采集信号为无效或者不符合换向次序规则(见表 1)时, 则认为该余度霍尔传感器故障。同时, 切换用于电机控制的主/备线圈, 接收霍尔传感器正常通道的驱动指令, 进而驱动电机按照正确的方向进行旋转。由此, 霍尔传感器完整的自监控设计, 能够保证用于位置传感器的解析模型的正确性。

2) 位置传感器的解析模型设计

霍尔传感器作为电机旋转速度的表征, 根据其采集信号的变化量, 可以计算得到电机旋转变化量。如图 1所示, 电机旋转需经过机械传动、输出机构等多层精密传动机构的级联, 才能形成位置传感器的变化。因此, 其传动比计算为

式中：K1是电机霍尔传感器与电机转速的比值；K2是电机与传动齿轮转速的比值；K3是传动齿轮与输出机构的比值。作为高精度电动伺服舵机, K可以达到105量级。

3) 位置传感器的故障诊断设计

以四余度位置传感器为例来进行故障诊断算法的设计。位置传感器的故障诊断采用多余度比较为主、霍尔传感器模型比较为辅的混合诊断方法, 形成完整的传感器故障诊断策略, 提升1∶1, 2∶2等奇异故障模式的检测和识别能力, 如图 4所示。

首先采用基于四余度比较的故障检测和识别方法, 由此可以根据多数服从少数的原则完成四余度信号的故障检测和识别, 同时将故障的传感器信号进行隔离, 避免进入控制回路影响控制精度。

其次, 当发生1∶1, 2∶2等奇异故障时, 引入基于霍尔传感器模型的故障检测和识别方法。因此, 基于霍尔传感器完整的自监控能力, 采用精确传动比的解析模型会始终跟踪着电动伺服舵机的实际旋转角度, 即位置传感器的输出值。那么, 当某个传感器故障引发某个余度的位置传感器逐渐发散，导致位置传感器比较出现奇异故障时, 基于霍尔传感器的解析模型值可以识别故障的位置传感器, 达到故障检测的目的。同时将故障的奇异传感器信号进行隔离, 使正常的传感器信号进入控制回路。

表1

电机换向时霍尔传感器逻辑表

thumbnail 图4

基于多余度比较与霍尔传感器的混合诊断结构

3 算法综合验证

为验证上述故障诊断算法的有效性和诊断效果, 重点针对传感器奇异情形下基于霍尔传感器模型的滑动数据窗故障诊断算法进行验证。以某型飞行器管理系统中电动伺服舵机的位置传感器为对象进行物理验证。

对于位置传感器这类旋转变压器式传感器, 考虑其传感器的方差包含本身传感器的测量白噪声σ1=1.2°, 以及残差系统生成时多个信号的测量白噪声σ2=1.7°, 那么最终合成方差为σ2=σ12+σ12, 求得σ=2.081°

传感器的双边采集范围为±60°, 幅值门限选择与与多余度比较方法相同(0.5%), 即为3.0°。应用定理1, 选定虚警率Pfn≤5%, 漏报率Pmn≤2%, 可以得到采用滑动数据窗方法的采集宽度为

采用所提基于霍尔传感器模型的故障诊断算法, 将电动伺服舵机的某个传感器固定轴(A/B通道传感器的安装位置)松动到一定程度, 在系统振动台架上进行物理台架验证, 试验条件和参数为：

1) 算法所运行的处理器为TMS320F2812的DSP处理器, 考虑到时间运算余量和存储空间余量, 为避免实际系统干扰等因素影响, 将采集宽度取整后放大为20个运行周期。

2) 结合实际高频振动环境, 为保证所提故障诊断算法的环境适应性, 按GJB-150.16A要求的图C.8振动条件, 在振动试验台架上模拟实际振动特性。

3.1 固定指令验证

在电动伺服舵机的闭环控制回路中, 给定固定指令分别为小指令(24.5°)、大指令(90°), 诊断算法的物理验证结果如图 5所示。其中，图 5a)和5c)中红圈位置对应的局部分大图分别如图 5b)和5d)所示。

图中各条曲线分别标识位置传感器的4个通道值、Hall模型值、表决值的变化过程。其中, 红色、蓝色曲线分别为A/B通道的通道值, 绿色、紫色曲线分别为C/D通道的通道值, 淡蓝色为基于霍尔传感器(图中简称Hall)的模型值, 橘色为表决值。

thumbnail 图5

固定指令时诊断算法的物理验证结果

3.2 正弦指令验证

在电动伺服舵机的闭环控制回路中, 给定正弦波形式的控制指令, 正弦波指令分别为小指令(24.5°)、大指令(90°), 其周期分别为4 Hz和8 Hz, 诊断算法的物理验证结果如图 6所示。

thumbnail 图6

不同正弦指令时诊断算法的物理验证结果

3.3 验证结果分析

从图 5中可以发现, 不论是在小指令还是大指令的控制状态下, Hall模型值始终与正常C/D通道的位置传感器通道值非常接近, 与故障A/B通道(传感器固定轴松动)的位置传感器通道值相差较大。

因此, 针对存在机械松动的位置传感器进行振动台架验证时, 常规的基于多余度比较的故障检测方法无法识别出故障A/B通道, 而当A/B通道的传感器通道值与C/D通道的传感器通道值连续出现20个运行周期的2∶2奇异故障时, 分别在第16 650、第11 638个运行周期, 及时、准确地识别和定位故障A/B通道的传感器。之后, 故障A/B通道的传感器被剔除，不再进入闭环控制回路, 随后由正常C/D通道的传感器闭环反馈进入电动伺服舵机控制回路, 实现闭环精确控制。

同样, 从图 6可以发现, 不论是在较低频率的4 Hz正弦波操纵、还是较高频率的8 Hz正弦波操纵的控制状态下, Hall模型值始终与正常C/D通道的位置传感器通道值非常接近, 与故障A/B通道(传感器固定轴松动)的位置传感器通道值相差较大。

同理，分别在第10 062、第13 811个运行周期，及时、准确地将故障A/B通道的传感器识别和定位出来。因此，基于霍尔传感器模型的奇异故障诊断算法不仅在固定常值指令时有效，在正弦波等运动指令过程中也非常有效。

从图 5~6所展示的结果可以看出, 在常规多余度比较监控的基础上, 增加2∶2等奇异故障情形时基于霍尔传感器模型的故障诊断算法, 能够有效解决2∶2等奇异故障带来故障诊断难题, 在保证闭环控制精度的同时, 能够大幅提升位置传感器信号的可用性。具体而言:

1) 不论是以固定值保持控制指令, 还是以正弦波形式给出控制指令时, 基于霍尔传感器模型的解析值始终跟踪着正常C/D通道的位置传感器值, 保证了模型的准确性和有效性。

2) 在模拟实际使用时的振动环境中, 随着故障A/B通道(传感器固定轴松动)持续偏离正常数值, 类似于发生斜坡式的故障模式时, A/B通道和C/D通道出现2∶2奇异故障, 传统基于多余度比较的故障诊断方法无法识别故障的A/B通道, 导致无法进行故障隔离, 故障的传感器数据依然会进入电动伺服舵机的控制回路, 出现控制精度下降的情形(表决值偏离正常C/D通道的数值)。

3) 基于霍尔传感器模型的奇异故障诊断算法, 能够在滑动数据窗方法设计的时间(20个运行周期)内, 准确、及时地识别故障A/B通道, 并将其剔除在表决值外, 利用正常C/D通道的表决值反馈进入电动伺服舵机的控制回路, 达成正常的闭环精确控制, 实现容错控制的设计目标, 进一步表明了基于模型的故障诊断算法的设计可行性和诊断准确性。

4) 避免了基于多余度比较的故障诊断算法在面对奇异故障时只能同步定位“4个通道的传感器均故障”的应用窘境, 降低多余度传感器信息的故障降级速度, 提升系统的整体容错能力。

4 结论

采用基于滑动数据窗的假设检验方法, 提出一种基于霍尔传感器模型(解析余度)的故障诊断方法, 与基于多余度比较的故障诊断方法进行综合, 由此形成的混合故障诊断方法能够有效解决当前难以处理的2∶2等奇异故障模式。

基于霍尔传感器完整的自监控设计、舵机位置传感器的解析模型设计, 创新性地构建出非相似余度信号, 能够有效辅助多余度物理传感器信号的故障诊断; 基于滑动数据窗的多样本检验方法, 通过调整滑动数据窗口的宽度, 可以同时满足故障检测对虚警率和漏报率的指标要求。

针对某电动伺服舵机的四余度位置传感器实际产品, 在物理验证环境下开展2∶2奇异故障模式的算法综合验证, 结果表明基于霍尔传感器模型的故障诊断算法, 能够及时、准确地识别故障余度的位置传感器信号, 保留正常余度的传感器信号, 有效解决了2∶2等奇异故障带来的诊断难题, 大幅提升传感器信号的可用性, 保证电动伺服舵机的变控制精度和系统容错能力。

References

  1. NIE Lei. Research on the system design and control of UAV electric servo[D]. Harbin. Harbin Institute of Technology, 2019 (in Chinese) [Google Scholar]
  2. ZHANG Mingyue. Design of control system for EMA based on TMS320F28335[J]. Electronic Design Engineering, 2019, 27(16) 189193 (in Chinese) [Google Scholar]
  3. YANG Inseok, KIM Donggil, LEE Dongik. Fault-tolerant control strategy based on control allocation using smart actuators[C]//2010 Conference on Control and Fault Tolerant Systems, Nice, France, 2010: 377–381 [Google Scholar]
  4. ZHANG J, SWAIN A K, NGUANG S K. Robust sensor fault estimation scheme for satellite attitude control systems[J]. Journal of the Franklin Institute, 2013, 350(9): 2581–2604 [Article] [CrossRef] [Google Scholar]
  5. JIANG BZHANG KLIU C, et al. Fault diagnosis and accommodation with flight control applications[J]. Journal of Control and Decision, 2020, 7(1): 24–43 [Article] [CrossRef] [Google Scholar]
  6. PARK Y J, FAN S K S, HSU C Y. A review on fault detection and process diagnostics in industrial processes[J]. Processes, 2020, 8(9) 1123 [Article] [CrossRef] [Google Scholar]
  7. ZHANG Jisen. Research on fault diagnosis and fault tolerant control of actuator loop based on observer[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2021 (in Chinese) [Google Scholar]
  8. SHI Junxian, ZHANG Wenguang, ZHANG Yan, et al. Application of RBF neural network based on PSO algorithm in fault diagnosis of actuation system[J]. Journal of Naval Aeronautical and Astronautical, 2011, 26(2): 131–135 (in Chinese) [Google Scholar]
  9. LI DWANG YWANG J, et al. Recent advances in sensor fault diagnosis: a review[J]. Sensors and Actuators A: Physical, 2020, 309: 111990 [Article] [NASA ADS] [CrossRef] [Google Scholar]
  10. DING S X. Model-based fault diagnosis techniques-design schemes, algorithms and tools[M]. London: Springer-Verlag, 2013 [CrossRef] [Google Scholar]
  11. GERTLER J J. Fault detection and diagnosis in engineering systems[M]. Boca Raton: CRC Press, 2017 [CrossRef] [Google Scholar]
  12. ZHANG Zhilong, CHEN Cen, SHI Junxian, et al. Fault diagnosis strategy of multi-valued attribute system based on improved artificial bee colony algorithm[J]. Journal of Naval Aeronautical and Astronautical, 2022, 37(3): 261–268 (in Chinese) [Google Scholar]
  13. SHABBIR WAIJUN LYUWEI C. Neural network-based sensor fault estimation and active fault-tolerant control for uncertain nonlinear systems[J]. Journal of the Franklin Institute, 2023, 360(4): 2678–2701 [Article] [CrossRef] [Google Scholar]
  14. HONARMAND-SHAZILEHEI F, PARIZ N, SISTANI M B N. Sensor fault detection in a class of nonlinear systems using modal Kalman filter[J]. ISA Transactions, 2020, 107: 214–223 [Article] [CrossRef] [Google Scholar]
  15. DENG Z, WANG H, WANG R. An improved unscented kalman filter for interrupted and drift sensor faults of aircrafts[J]. IEEE Trans on Instrumentation and Measurement, 2023, 72: 3505310 [Google Scholar]
  16. ABBASPOUR A, ABOUTALEBI P, YEN K K, et al. Neural adaptive observer based sensor and actuator fault detection in nonlinear systems: application in UAV[J]. ISA Transactions, 2017, 67: 317–329 [Article] [CrossRef] [Google Scholar]
  17. CHI Chengzhi. Research on fault-tolerant flight control technology based on redundancy strategy[D]. Xi'an: Northwestern Polytechnical University, 2013 (in Chinese) [Google Scholar]
  18. XU Yanling, ZHANG Xinguo, WANG Lin. Quadruplex FBW redundant schemes and its application in practice[J]. Measurement & Control Technology, 2008, 27(11) 11–13 (in Chinese) [Google Scholar]
  19. WANG Ziling, XU Aiqiang, LIN Xueyuan, et al. An optimal design algorithm of redundant system diagnostic stategy[J]. Journal of Naval Aeronautical and Astronautical, 2013, 28(5): 539–542 (in Chinese) [Google Scholar]
  20. ZHANG ZYANG ZLIU S, et al. A multi-model based adaptive reconfiguration control scheme for an electro-hydraulic position servo system[J]. International Journal of Applied Mathematics and Computer Science, 2022, 32(2) 185–196 [Google Scholar]
  21. HUANG W, XU H, WANG J, et al. Redundancy management for fault-tolerant control system of an unmanned underwater vehicle[C]//20205th International Conference on Automation, Control and Robotics Engineering, 2020: 291–296 [Google Scholar]
  22. GAO SMA GGUO Y, et al. Fast actuator and sensor fault estimation based on adaptive unknown input observer[J]. ISA Transactions, 2022, 129: 305–323 [Article] [CrossRef] [Google Scholar]
  23. MOHAMMADI ARAMEZANI A. An active actuator fault-tolerant control of a quadrotor based on analytical redundancy relations[J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2020, 44(3): 1069–1079 [Article] [CrossRef] [Google Scholar]
  24. MOHAMMADI A, RAMEZANI A. An analytical robust sensor fault detection and fault tolerant control in quadrotor[J]. Automatic Control and Computer Sciences, 2021, 55(1): 38–52 [CrossRef] [Google Scholar]
  25. CUI Zhonglin, ZHU Chengxiang, YUAN Liaoyuan. Research on fault tolerant design of angular velocity sensor based on analytic signal[J]. Electronic Technology & Software Engineering, 2021(12): 86–89 (in Chinese) [Google Scholar]

All Tables

表1

电机换向时霍尔传感器逻辑表

In the text

All Figures

thumbnail 图1

电动伺服舵机控制回路框图
In the text
thumbnail 图2

奇异故障时引入解析模型的故障诊断框图
In the text
thumbnail 图3

滑动数据窗方法的测量信号采集示意图
In the text
thumbnail 图4

基于多余度比较与霍尔传感器的混合诊断结构
In the text
thumbnail 图5

固定指令时诊断算法的物理验证结果
In the text
thumbnail 图6

不同正弦指令时诊断算法的物理验证结果
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.