| Issue |
JNWPU
Volume 37, Number 6, December 2019
|
|
|---|---|---|
| Page(s) | 1278 - 1284 | |
| DOI | https://doi.org/10.1051/jnwpu/20193761278 | |
| Published online | 11 February 2020 | |
Fault Diagnosis and Compensation Strategy of BLDC Motor Drives with Hall Sensors
无刷直流电机霍尔传感器故障诊断与补偿策略
School of Automation, Northwestern Polytechnical University, Xi'an 710129 China
Received:
20
December
2018
In a brushless DC motor drive system, two fault diagnosis methods were proposed in order to investigate the faults of Hall position sensors, and the corresponding compensation strategy was carried out. Firstly, the differences of Hall signal sequences during normal and fault situation of motor were analyzed, then a fault diagnosis method based on the characteristics of Hall signal sequences was proposed. In order to detect the faults of Hall position sensors in real time, a sliding mode-based super-twisting speed observer was established and combined with the Hall signal sequences. Under fault situations, the compensation controller was established, and a second-order speed prediction method was used to generate the compensation Hall signals of the faulty sensors. Finally, theoretical analysis and experiments demonstrate the effectiveness of the present fault diagnosis methods and compensation strategy.
摘要
针对无刷直流电机霍尔位置传感器故障,提出了2种故障诊断方法,并进行了相应的补偿控制。首先,分析了电机正常运行过程中的霍尔信号序列特征,提出了以故障后霍尔信号序列特征作为诊断依据的故障诊断方法。同时,为实时检测发生在某些扇区的传感器故障,建立了基于滑模的超螺旋转速观测器,并将其与霍尔信号序列检测相结合,实现了高实时性的故障检测。在此基础上,以正常位置传感器信号作为基础,利用二阶转速预测信息和理想霍尔信号序列实时生成补偿霍尔信号,建立了故障信号的补偿控制器。最后,通过理论分析和实验验证了所提故障诊断与补偿策略的有效性,提高了无刷直流电机驱动系统的可靠性与安全性。
Key words: brushless DC motor / hall position sensors / fault diagnosis / super-twisting observer / compensation strategy
关键字 : 无刷直流电机 / 霍尔位置传感器 / 故障诊断 / 超螺旋观测器 / 补偿策略
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
无刷直流电机(brushless DC motor)一般采用结构简单的霍尔传感器作为转子位置传感器,具有功率密度高、调速性能好等优点,广泛应用于工业和商业领域各类电驱动系统中[1-4]。当电机的霍尔传感器发生故障时,则会引起巨大的异常电流,甚至对整个电驱动系统造成破坏。因此,有关无刷直流电机的霍尔传感器故障诊断与容错控制研究对提高电驱动系统的可靠性有十分重要的意义[5-7]。
在文献[8]中,Scelba将霍尔信号进行坐标变换至α-β坐标系后,通过检测霍尔信号的零矢量作为故障诊断依据,并分析了不同传感器故障之后霍尔信号序列的变化情况,以此定位故障的传感器。文献[9]将故障后的霍尔信号以及跳变沿信号序列一一列举出来,对比分析了几种故障诊断方法的效果,并进行了相应的容错控制。在电机实际运行过程中,控制系统需要实时获取霍尔传感器反馈的转子位置信息,并选择合适的驱动电压矢量施加在驱动桥臂上。而霍尔位置传感器一旦发生故障,其包含的位置信号随即丢失。此时如果故障并未被检测出来,则控制系统仍会按照霍尔传感器反馈的错误位置信息施加驱动电压。在错误的驱动电压作用下,电机未必能够维持原来的转向和转速,这将导致电机转速失调,甚至给电驱动系统造成更大的损坏。
本文在以往相关研究的基础上,对无刷直流电机的霍尔位置传感器故障诊断与补偿策略进行了综合性的研究。首先分析了电机运行过程中,正常情况下的霍尔信号状态特征;然后提出了一种基于霍尔信号状态的故障诊断方法,并建立了基于超螺旋算法的转速观测器,将其与霍尔信号状态结合,实现了对霍尔传感器故障的实时检测;最后提出了基于二阶转速预测的补偿控制算法,并通过实验验证了以上所提霍尔传感器故障诊断方法以及相应补偿策略的有效性。
1 电机霍尔传感器故障分析
1.1 系统模型与分析
无刷直流电机在运行过程中,需要由3个两两之间相隔120°的霍尔位置传感器实时反馈其转子位置信息。每当转子磁极经过某个霍尔传感器附近时,该传感器会发出高电平或低电平信号,对应到控制系统采集的信号则是“1”或“0”。为便于后面的分析,一个简化的电机霍尔信号示意图如图 1所示(以逆时针方向为正向)。
由图 1可以发现, 电机被3个霍尔传感器Ha, Hb, Hc分为6个扇区, 转子在每个扇区时霍尔传感器即会反馈相对应的信号, 转动一圈共有6个不同霍尔信号出现。当转子由一个扇区切换至下一个扇区时, 霍尔信号会有相应跳变, 称之为一个跳变沿(Edge), 以Ea为例,定义跳变沿信号如下
无刷直流电机运行时的动态模型可以表示为
式中, ωr为电机角速度, J为转动惯量, Bv为旋转阻尼系数, Te为电磁转矩, kT为转矩常数, i为电枢电流, TL为负载转矩, L为定子电感, R为定子电阻, ea为电机反电势, kb为反电势常数, Ua为电枢电压。
如果电机3个霍尔传感器全部正常, 转子进入每个扇区时, 都会有相应霍尔传感器出现跳变沿信号, 同时其他2个霍尔传感器信号保持不变。将转子进入某扇区时的跳变沿信号以及与其对应的其他2个霍尔信号统称为霍尔状态信号, 以电机正转为例, 转子进入每个扇区时的正常霍尔状态信号如表 1所示:
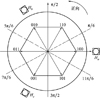 |
图1 正常霍尔信号 |
正常霍尔状态信号
1.2 霍尔传感器故障
本文主要考虑无刷直流电机1个或2个霍尔传感器出现故障时, 电驱动系统的故障诊断及其补偿控制。当3个霍尔传感器全部故障时, 电机转子的位置信息全部丢失, 电驱动系统需增加额外的硬件电路进行无位置控制, 此处不再讨论。
当某个霍尔传感器故障时, 其输出的信号不再随电机转子的位置发生变化, 保持在固定的高电平或低电平(“1”或“0”)不变, 不再反映转子的位置信息。以传感器Ha故障为高电平时为例, 故障发生之后相应的霍尔信号如图 2所示, 霍尔信号只有4个不同值, 其余的单传感器故障霍尔信号图也都如此。类似的有双传感器故障时的霍尔信号图, 故障后霍尔信号只剩2个不同值。
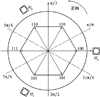 |
图2 单传感器故障霍尔信号 |
2 霍尔传感器故障诊断及补偿策略
2.1 基于霍尔状态信号的故障诊断方法(M1)
电机正常转动过程中, 转子在进入不同扇区时会出现不同跳变沿信号, 这些跳变沿信号表示电机转子处于图 1中某2个扇区的交界处; 不同的霍尔信号则表示电机转子处于6个不同扇区的角度范围之中。霍尔传感器全部正常时, 每个跳变沿信号都对应其他2个固定的霍尔信号, 二者为一一对应关系, 如1.1小节中表 1所示。
当某个霍尔传感器发生故障时, 随着电机转子转动, 总会在某个扇区里出现异于表 1中的霍尔状态信号, 以f1, f2, f3分别表示相应霍尔传感器Ha, Hb, Hc故障, 建立单传感器故障状态表如表 2所示, 类似的还有双传感器故障状态表, 文中不再详细列举。相较于其他研究, 如文献[9]所提的故障检测方法, 需要连续检测到某些特定的故障霍尔信号序列, 才能诊断出故障的传感器; 利用本文所提故障诊断方法, 只需在每次检测到异于表 1中的霍尔状态信号时, 将其与所建立的故障状态表中数据进行对比, 即可分辨出相应的故障传感器, 算法效率更高(为方便后文描述, 将此故障检测方法记为M1)。
单传感器故障霍尔状态信号
2.2 基于转速观测器的故障诊断方法(M2)
霍尔传感器故障发生时, 电机转子可能处于图 1中6个扇区里的任意一个, 对于转子处于某些扇区时发生的故障, 使用诊断方法M1可以立刻检测出来; 而当转子处于其他扇区时发生的故障, 则需要转子再转过几个扇区才能检测到相应的故障信号, 下面以图 3所示的故障情况进行分析, 传感器Ha在刚进入7π/6~3π/2扇区时即故障为高电平。
分析图 3中各信号可以发现, 此故障信号初始时只是相当于正常信号提前一段时间跳变, 无论是霍尔信号或霍尔信号序列, 还是跳变沿信号及其对应的霍尔信号状态表, 均与正常状态无异, 如果转子能够维持原方向转动, 则只有在故障后的第5个扇区, 即5π/6~7π/6扇区, 才能检测到相应的故障信号。
然而在故障被检测到之前, 控制系统仍会按照霍尔传感器反馈的位置信号在出现故障后的7π/6~3π/2和π/2~5π/6扇区施加错误的驱动电压矢量, 在错误的驱动电压矢量作用下电机未必能保持故障之前的转速和转向, 甚至电驱动系统可能已经过流保护并停止运行。因此仅依靠霍尔信号或跳变沿信号, 不能及时将发生在某些扇区的故障检测出来, 还需要将转速信息与霍尔信号状态结合起来进行故障检测。
由(2)至(3)式中电机的动态方程可以发现, 电机转速信息还存在于其动态模型中, 下面将电机转速作为一个未知量, 设计一个转速观测器[10]
式中, 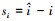 , ξ(si)为基于线性超螺旋算法的鲁棒项。
, ξ(si)为基于线性超螺旋算法的鲁棒项。
ξ(si)可由(5)式表示
由(2)式和(4)式可得
令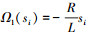 和
和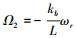 表示扰动项, (6)式可表示为
表示扰动项, (6)式可表示为
由于i,TL,J,Bv均有界, 故存在常数ρ1和ρ2, 使得(8)式成立
如果(9)式满足, 可使上述估计值的误差收敛[11]
估计转速可以表示为
假设在tn时刻检测到一个表 1中正常的跳变沿信号, 前一个跳变沿信号时刻为tn-1, 则此2个跳变沿间电机的平均转速为
此时估计转速与实际转速的误差残值可以表示为:
设定一个转速误差阈值ωres, 根据转速误差残值与阈值的大小即可进行相应的故障诊断
以图 3所示霍尔传感器故障为例, 如果电驱动系统中霍尔传感器发生相应故障, 诊断方法M1在故障发生后的第5个扇区才能检测出故障信号; 而诊断方法M2在故障发生处的扇区即可检测出故障信号, 故障诊断效果较M1更加实时与高效。
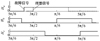 |
图3 Ha在7π/6~3π/2扇区故障为高电平 |
2.3 基于二阶转速预测的故障补偿策略
预测控制是一种基于预测变化趋势对控制系统进行调节的算法, 本文主要将预测控制用于位置传感器故障后的霍尔信号补偿, 下面以图 3中故障为例分析。
假传感器Ha发生故障前的一个跳变沿时刻为tn, 类似的还有之前的跳变沿时刻tn-1, tn-2, tn-3, 下面结合表 1中正常霍尔信号状态, 利用剩余正常霍尔传感器Hb, Hc的信号估计故障传感器Ha的下一个跳变沿时刻tn+1, 取
电机转速变化量可表示为
然后可以得到
可以估计
最终可得Ha跳变沿时刻估计值
利用剩余正常霍尔传感器的信号与前面正常霍尔信号状态表, 即可实时生成故障传感器的补偿霍尔信号序列。
系统整体结构如图 4所示, 当系统检测到新的霍尔状态信号时, 如果此信号异于表 1中正常信号, 即查询所建故障状态表并识别相应的故障传感器; 如果与表 1中正常信号相同, 再通过超螺旋转速观测器进行转速残值计算, 若超过阈值则输出相应故障信号。当某传感器故障被识别之后, 故障补偿模块以实时生成的故障补偿信号替代故障霍尔信号, 作为新的霍尔换相信号, 进行相应的故障补偿控制。
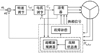 |
图4 控制系统整体结构 |
3 实验结果
为验证所提故障诊断方法与补偿策略的有效性, 通过额定功率为35 W的无刷直流电机进行实验。电机参数如表 3所示, 电机驱动系统实验平台如图 5所示。驱动控制系统采用TMS320F2812控制的三相全桥驱动器, 控制算法均在主控芯片中实现, 实验数据通过控制芯片保存, 并使用Matlab绘制实验波形。
无刷直流电机驱动系统参数
 |
图5 电机驱动系统实验平台 |
3.1 故障诊断效率对比
首先对建立的超螺旋转速观测器效果进行测试, 在正常情况下, 给定电机初始转速为200 r/min, 并在t=0.2 s至0.4 s处将给定转速提升至1 000 r/min, 电机实际转速以及转速观测器估计转速如图 6至7所示。在电机转速保持不变时, 估计值与实际值误差保持在20 r/min左右, 电机转速上升过程中误差残值也控制在50 r/min以内, 后面故障检测过程中也依此设定转速误差阈值为50 r/min。
上述实验结果表明, 建立的转速观测器能有效跟踪和反映电机实际转速, 可作为故障检测环节的实时转速参考值。
对前面所提故障诊断方法M1与M2的实验效果进行对比。给定电机初始转速为1 000 r/min, 并在t=0.208 s处使霍尔传感器Ha故障为高电平, 如图 8所示。
故障诊断方法M1在进行故障检测的过程中, 需要检测到表 2中故障霍尔信号状态才会输出相应霍尔传感器故障信号, 但此处故障在初始时相当于霍尔信号Ha提前跳变至高电平, 在霍尔序列上并不会反映出故障信息, 直至t=0.214 s时Hc跳变至高电平信号时, 才会在霍尔序列上反映表 2中的故障信息, 如图 9所示。
故障诊断方法M2在进行故障检测时, 转速观测器输出的估计转速值在霍尔故障发生时并不会突变。由霍尔信号计算的实际转速则在故障发生时产生突变, 二者误差在超过设定的误差阈值50 r/min后, 如图 10所示, 可在故障发生之时的t=0.208 s处检测到故障并输出图 9中相应的故障信号。
对比2种故障诊断方法的实验结果可以发现, 方法M2比方法M1能够更快速地将霍尔传感器故障诊断出来, 不仅能提高系统故障诊断的效率, 也为后续的故障霍尔信号补偿控制提供了更好的基础。
 |
图6 转速估计值与实际值对比 |
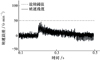 |
图7 转速误差残值对比 |
 |
图8 故障霍尔信号 |
 |
图9 故障检测效果对比 |
 |
图10 故障检测时转速误差残值 |
3.2 故障补偿控制效果
霍尔传感器故障被诊断出来之后, 需对故障信号进行补偿重构, 并替代故障的霍尔信号作为新的换相信号, 下面对前面所提故障补偿控制策略进行实验验证。
首先给定电机转速参考值1 000 r/min, 电机运行平稳之后, 在t=0.31 s处使霍尔传感器Ha突变为高电平“1”并保持不变, 如图 11所示。在故障被诊断出来之后, 故障补偿控制器开始介入并将补偿信号替代故障的霍尔信号, 故障补偿后的电机转速相对于正常时转速波动仅有30 r/min左右, 如图 12所示, 在可接受范围之内。同时, 故障时的瞬时电流也只有1.5 A, 稳定之后三相电流相对于正常时电流值仅增加0.3 A, 如图 13所示。
实验结果表明, 在单霍尔传感器故障情况下, 前面所提故障补偿控制策略能够使系统快速地从故障中恢复运行, 并保持电机转速和电流稳定。双霍尔传感器故障时的补偿控制实验效果与上述实验结果类似, 此处不再详细列举。
 |
图11 霍尔传感器Ha故障 |
 |
图12 电机转速 |
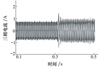 |
图13 三相电流信号 |
4 结论
本文针对无刷直流电机的霍尔传感器故障诊断与补偿控制进行了研究。文章首先分析了电机霍尔传感器正常与故障情况下的不同霍尔信号状态特征,提出了基于霍尔信号状态的故障诊断方法,然后根据电机动态模型建立了超螺旋转速观测器,并将其与霍尔信号状态的故障诊断方法结合,使之能够实时诊断出发生在任意扇区中的霍尔传感器故障。最后,利用基于二阶转速预测的故障补偿策略生成故障霍尔传感器的补偿信号,并替代故障的霍尔信号,实现了霍尔传感器的故障补偿控制。实验结果表明,本文所提控制方法可实时检测到电机的霍尔传感器故障,并施加相应补偿控制措施,提升了无刷直流电机驱动系统的可靠性。
References
- Alaeinovin P, Jatskevich J. Filtering of Hall-Sensor Signals for Improved Operation of Brushless DC Motors[J]. IEEE Trans on Energy Conversion, 2012, 27(2): 547–549 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Jiang Weidong, Liao Yuming, Wang Jinping, et al. Improved Control of BLDCM Considering Commutation Torque Ripple and Commutation Time in Full Speed Range[J]. IEEE Trans on Power Electronics, 2018, 33(5): 4249–4260 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen N K, Meinguet, Semail E, et al. Fault-Tolerant Operation of an Open-End Winding Five-Phase PMSM Drive with Short-Circuit Inverter Fault[J]. IEEE Trans on Industrial Electronics, 2016, 63(1): 595–605 [Article] [CrossRef] [Google Scholar]
- Chen Wei, Liu Zhibo, Cao Yanfei, et al. A Position Sensorless Control Strategy for the BLDCM Based on a Flux-Linkage Function[J]. IEEE Trans on Industrial Electronics, 2019, 66(4): 2570–2579 [Article] [CrossRef] [Google Scholar]
- Dong Lianghui, Jatskevich J, Huang Yingwei, et al. Fault Diagnosis and Signal Reconstruction of Hall Sensors in Brushless Permanent Magnet Motor Drives[J]. IEEE Trans on Energy Conversion, 2016, 31(1): 118–131 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Dong Lianghui, Huang Yingwei, Jatskevich J, et al. Improred Fault-Tolerant Control for Brushless Permanent Magnet Motor Orives with Defecftive Hall Sensors[J]. IEEE Transactions on Energy Conversion, 2016, 31(2): 789–799 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Kim S Y, Choi C, Lee K, et al. An Improved Rotor Position Estimation with Vector-Tracking Observer in PMSM Drives with Low-Resolution Hall-Effect Sensors[J]. IEEE Trans on Industrial Electronic, 2011, 58(9): 4078–4086 [Article] [CrossRef] [Google Scholar]
- Scelba G, De Donato G, Scarcella G, et al. Bonaccorso Fault-Tolerant Rotor Position and Velocity Estimation Using Binary Hall-Effect Sensors for Low-Cost Vector Control Drives[J]. IEEE Trans on Industry Applications, 2014, 50(5): 3403–3413 [Article] [CrossRef] [Google Scholar]
- Dong Lianghui, Liu Jinglin. Fault Detection and Fault Tolerant Control of Permanent Magnet Synchronous Motor Drives with Hall Sensors[J]. Journal of Northwestern Polytechnical University, 2016, 34(2): 306–312 [Article] (in Chinese) [Google Scholar]
- Kommuri S K, Rath J J, Veluvolu K C. Sliding-Mode Based Observer-Controller Structure for Fault-Resilient Control in DC Servomotors[J]. IEEE Trans on Industrial Electronics, 2018, 65(1): 918–929 [Article] [CrossRef] [Google Scholar]
- Moreno J A, Osorio M. Strict Lyapunov Functions for the Super-Twisting Algorithm[J]. IEEE Trans on Automatic Control, 2012, 57(4): 1035–1040 [Article] [Google Scholar]
All Tables
All Figures
 |
图1 正常霍尔信号 |
| In the text | |
 |
图2 单传感器故障霍尔信号 |
| In the text | |
 |
图3 Ha在7π/6~3π/2扇区故障为高电平 |
| In the text | |
 |
图4 控制系统整体结构 |
| In the text | |
 |
图5 电机驱动系统实验平台 |
| In the text | |
 |
图6 转速估计值与实际值对比 |
| In the text | |
 |
图7 转速误差残值对比 |
| In the text | |
 |
图8 故障霍尔信号 |
| In the text | |
 |
图9 故障检测效果对比 |
| In the text | |
 |
图10 故障检测时转速误差残值 |
| In the text | |
 |
图11 霍尔传感器Ha故障 |
| In the text | |
 |
图12 电机转速 |
| In the text | |
 |
图13 三相电流信号 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


