| Issue |
JNWPU
Volume 38, Number 1, February 2020
|
|
|---|---|---|
| Page(s) | 121 - 129 | |
| DOI | https://doi.org/10.1051/jnwpu/20203810121 | |
| Published online | 12 May 2020 | |
Comparative Study on Modal Decomposition Methods of Unsteady Separated Flow in Compressor Cascade
压气机叶栅非定常分离流动的模态分解方法对比研究
1
School of Power and Energy, Northwestern Polytechnical University, Xi'an 710072, China
2
Yangtze River Delta Research Institute of Northwestern Polytechnical University, Taicang 215400, China
3
Beijing Changcheng Institute of Metrology and Measurement, Beijing 100095, China
Received:
1
April
2019
The present work investigated the vortex structure and fluctuation frequency characteristics generated by boundary layer separation of a high-load compressor cascade using modal decomposition methods. The dominant modes and dynamic behaviors of unsteady flow in the cascade were obtained, and the differences of three modal decomposition methods (Proper Orthogonal Decomposition, Dynamic Mode Decomposition and Spectral Proper Orthogonal Decomposition) in feature recognition of cascade flow were discussed. The results show that:(1) The POD method can accurately extract the dominant spatial structure of the flow field, but the modal coefficients are multi-frequency coupled, which makes the dominant modal characteristics of cascade flow unclear. (2) The standard DMD method can obtain the spatial-temporal single frequency mode of cascade flow, as well as their growth rates and frequencies. However, this method is likely to capture the suboptimal mode of large amplitude with large attenuation rate, and fails to obtain the high-frequency coherent structure, which makes it impossible to obtain the dominant feature with limited mode number. (3) The SPOD method, based on spectral characteristics, can obtain spatial and temporal single frequency modes, and there is no modal screening problem. The use of spectral estimation method (SPOD) reduces the sensitivity to numerical noise. This method can obtain the low-rank behavior of cascade flow, which is helpful to understand cascade flow mechanisms. Therefore, SPOD method is more advantageous for the modal analysis of unsteady separated flow in high-load compressor cascade.
摘要
以某高负荷压气机叶栅为研究对象,应用模态分解方法研究叶栅附面层分离所产生的旋涡结构形式和波动频率特征,获得了叶栅非定常流动的主导模态和动态行为,探讨了3种模态分解方法(本征正交分解(POD)、动态模态分解(DMD)和谱本征正交分解(SPOD))在叶栅流动特征识别的差异性。研究结果表明:①POD方法准确提取叶栅分离流动主要空间结构,但模态系数存在多频率耦合问题,导致对于叶栅流动的主导模态特征无法清晰识别;②标准DMD方法可以获得叶栅流动时空单频模态,及其增长率和频率,但是该方法捕捉到流场大衰减率的大振幅次优模态,未能获得高频相干结构,导致无法用有限的模态数得到主导特征;③基于谱特征的SPOD方法能够获得时空单频模态,且不存在模态筛选问题,谱估计方法的使用降低了对数值噪声的敏感性,同时该方法获得了叶栅流动的低秩行为,有助于增强对叶栅流动机理的理解。因此,对高负荷压气机叶栅分离流动进行模态分析时,SPOD方法更具优势。
Key words: proper orthogonal decomposition / dynamic mode decomposition / spectral proper orthogonal decomposition / single frequency mode / cascade flow mechanisms
关键字 : 本征正交分解 / 动态模态分解 / 谱本征正交分解 / 单频模态 / 叶栅流动机理
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
现代叶轮机械性能的提高得益于设计者对其内部流动特性的深入认识, 而随着流体力学领域全场动态参数精细化测量, 以及高精度数值模拟技术的发展, 非线性、非定常流场数据量呈指数级增长, 对海量数据高效的计算与分析成为制约相关理论进一步发展的重要因素。为了提高对复杂非定常流场大数据的提取与分析效率, 加深对流动相干结构与机理的认识, 研究人员结合数据降维技术, 发展了多种非定常流场模态分解方法, 并将这些方法广泛应用于叶轮机械流固耦合[1]、气动优化设计[2]和流动精细化控制[3]等领域, 取得了大量有价值的研究成果, 展现出广阔的应用前景。
本征正交分解方法[4](proper orthogonal decomposition, POD)是最早提出的模态分解方法。其本质是寻找一组低维正交子空间, 将高维非定常流场投影到子空间上, 获得按照能量降序排列的各阶模态, 较少的几个高阶POD模态即可保留绝大部分能量。POD方法已经大量应用于研究多种流动问题, 例如方柱绕流的主导特征结构分析[5], NACA翼型的尾缘脱落涡[6], 以及压气机内部流动系统辨识[7]等, 均表现出了较好的模态分解性能, 但对于能量较低且接近主导频率的流动状态, POD方法可能难以获得相干结构。
不同于POD方法, 按照模态振幅对系统排序并提取主导特征的标准动态模态分解方法[8](dynamic mode decomposition, DMD), 可以得到具有单一频率和增长率的主导模态, 适合于周期性流动的结构分析。DMD方法的本质是将流动演化看作线性动力学过程, 通过对整个过程的流场快照进行特征分析, 得到表征流场信息的低阶模态。该方法也已经大量应用于流体力学问题研究, 包括亚临界圆柱涡致振动特性分析[9], 机翼的动态失速分析[10]以及跨声速抖振分析[11]等。DMD方法具有的时空耦合特性, 使得该方法在具有典型频率成分的流动问题上发挥优势, 但是该方法提取模态未能考虑到自身稳定性特征, 提取的模态可能不具有代表性[12]。
为获得时空耦合的真实流场单频物理模态, 在空间POD方法的基础上, 采用离散傅里叶变换(discrete fourier transform, DFT), 兼顾流场频域信息, 即谱本征正交分解方法[13](spectral proper orthogonal decomposition, SPOD), 也已经应用于多个领域。如翼型绕流的尾缘声辐射相干结构分析[14], 以及风力涡轮远场尾迹流动与圆柱绕流动力学的区别与联系[15]等复杂系统。SPOD方法类型较多, 本文采用的是Aaron等[13]在研究射流波包形态分析中发展的方法。SPOD方法能够获得流场各频率不同能级的模态, 以及流动的低秩行为, 为研究者提供更多有价值的流场相干结构。
从公开文献来看, 不同模态分解方法各有特点, 且均能有效分析流场相干结构。目前模态分解方法主要集中于外流和射流等领域, 对于叶轮机械高维、复杂非定常内流的相关研究较少, 外流的研究结果是否适用于内流仍需要深入研究, 各种模态分解方法的差异也值得关注。因此, 本文以具有典型分离流动的高负荷压气机叶栅为对象, 研究不同模态分解方法对叶栅附面层分离所产生的旋涡结构形式以及波动频率特征辨识, 获取叶栅非定常流动的主导模态和动态行为方面的差异。为精细化识别压气机叶栅非定常分离流动中多尺度、多频能级分布的流动结构提供适用准则, 为进一步实施精细化流动控制提供指导性理论依据。
1 模态分解方法
POD、DMD和SPOD模态分解方法均是通过提取时间序列的流场快照主要成分, 实现非定常流动分析。
1.1 POD方法
令{u(x, ti):x∈Ω, 1≤i≤N}为N个流场快照, Ω为流场所在物理区域, 快照可以表示为平均值和脉动量的组合: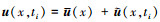 。POD的基本思想是将该过程的脉动量分解为时间系数和空间模态的序列, 即
。POD的基本思想是将该过程的脉动量分解为时间系数和空间模态的序列, 即
式中,{φj(x):x∈Ω, 1≤j≤N}为POD空间模态(通常称为POD基)。求解POD基需要计算相关矩阵C, 定义为
求解相关矩阵C的特征值问题获得时间系数aj=[aj(t1), …, aj(tN)]T和模态能量λj, 其中模态能量降序排列。POD基定义为
截取前M个主要基模态, 通过(1)式可得到任意时刻流场脉动量, 并重构流场。
1.2 DMD方法
将N个非定常流场快照按时间写成序列, 即{u1, u2, …, uN}, 且任意2个快照之间的时间间隔均为Δt, 引入线性映射假设:ui+1=Aui。利用N个时刻流场快照构建2个快照矩阵
DMD方法在于寻找矩阵A的较低维相似矩阵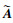 。为获得相似变换的正交子空间, 对秩为r的矩阵X做奇异值分解:X=UΣVH, 且令:
。为获得相似变换的正交子空间, 对秩为r的矩阵X做奇异值分解:X=UΣVH, 且令: 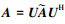 , 因此矩阵A可以近似为
, 因此矩阵A可以近似为
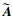 的特征值是A的Ritz特征值。记
的特征值是A的Ritz特征值。记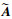 的第j个特征值为μj, 特征向量为δj, 则第j个DMD模态为
的第j个特征值为μj, 特征向量为δj, 则第j个DMD模态为
第j个模态对应的增长率和频率分别为:gj=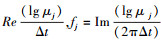 。定义W为特征向量δj的矩阵, N为特征值μj的对角阵, 任意时刻的快照可以估计为
。定义W为特征向量δj的矩阵, N为特征值μj的对角阵, 任意时刻的快照可以估计为
模态振幅α定义为
式中, αi为第i个模态振幅, 代表了该模态对初始快照u1的贡献。对于标准DMD方法, 模态按照该振幅排序。定义损失函数
式中:Dα为模态振幅对角阵; Vand为特征值范德蒙行列式。
1.3 SPOD方法
构建快照矩阵U=[u1, u2, …, uN], 借助Welch方法, 将快照矩阵U划分为多个有重叠的分块矩阵, 定义分块快照矩阵为
式中:Nb为分块数量;Nf为每个分块的快照数量。
定义第n个分块的第k个快照为
式中,No为分块之间重叠的快照数量。对每个分块快照矩阵使用DFT, 得到快照矩阵记为
此时, 第n个分块的第k个快照为
权值wj是窗口函数的节点值, 用来减少由于每个分块数据的非周期性而导致的谱泄漏。频率为fk的相关矩阵Cfk定义为
式中,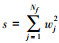 。将每个分块的傅里叶分量按照频率fk排列, 引入新的快照矩阵
。将每个分块的傅里叶分量按照频率fk排列, 引入新的快照矩阵
式中,χ=Δt/(sNb)。从而, 相关矩阵Cfk可表示为
求解每个频率相关矩阵的特征值问题即可获得SPOD模态, 该部分同POD方法。
2 非定常流场求解
2.1 研究对象
本文所研究压气机叶栅主要设计参数如表 1所示, 图 1给出了叶栅几何结构示意图。
叶栅主要设计参数
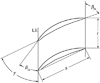 |
图 1 叶栅几何结构示意图 |
2.2 数值方法及验证
计算域进口距离叶栅前缘1倍弦长, 出口距离尾缘1.5倍弦长。采用H-O-H结构化网格, 总网格数30 196, 近壁面网格y+ < 1, 图 2为网格拓扑图。针对该二维平面叶栅, 采用ANSYS Fluent软件求解URANS方程, 采用k-ω SST湍流模型, 计算了来流马赫数0.6, 攻角4°非定常数值结果。时间步长为4×10-5s。图 3给出该工况非定常数值计算的叶栅壁面无量纲压力均值, 与试验测点均值的对比[7]。可以看出, 计算与试验测量压力分布吻合较好。表明采用的数值方法可以较好地预测叶栅气动参数及其变化规律。
数值稳定后, 每隔一个物理时间步选取快照, 选择模态分解的快照变量为各网格点压力。模态分解方法在非定常流场分析应用中, 研究人员均采用几百个快照不等。本文SPOD方法设定相邻分块矩阵快照重叠率50%。考虑到Fourier变换需尽可能采用数量为2的整数次幂的数据, 因此设定每个分块矩阵包含64个快照。本文一共设定了19个分块矩阵, 总的快照数量为64×(19+1)/2=640个。
 |
图 2 网格拓扑图 |
 |
图 3 无量纲压力分布图 |
3 非定常流动分析
对于压气机叶栅的过渡工况(吸力面出现分离涡), 通过POD、DMD和SPOD研究附面层分离所产生的旋涡结构形式以及波动频率特征, 对比3种模态分解方法的辨识差异。
图 4给出压气机叶栅非定常全局流场瞬时涡量图。可以看出, 本文叶栅流场波动主要体现在尾缘之后, 因此本文模态分析集中在尾迹区域。
图 5为该区域局部图。
可以看出, 流场涡系主要由叶栅吸力面分离涡和尾缘脱落涡组成, 两者反向交替离开叶栅尾缘, 结合图 6叶表静压力积分随时间变化功率谱密度图(power spectral density, PSD), 表明流场只有一个基频, 即该工况分离涡与脱落涡频率一致。
 |
图 4 全局流场瞬时涡量图 |
 |
图 5 局部流场瞬时涡量图 |
 |
图 6 叶表静压力积分功率谱密度图 |
3.1 POD分解
图 7给出了POD前30阶模态能量分布图。可以看出, 相邻模态的能量占比接近, 均成对出现, 且前2阶模态包含了绝大部分能量, 高阶模态对流场能量的贡献基本可以忽略。对于本文叶栅非定常分离流动, 前6阶模态包含了超过99.99%的流场能量, 故前6阶模态能够反映流动的主要相干结构。
图 8所示为POD前6阶模态云图。可以看出, 同一阶模态结构沿流向正负交替成对出现, 且相邻模态结构相似, 仅存在π/2的相位滞后(定义2个负涡核为一个周期2π)。叶栅尾缘脱落涡波动较吸力面分离涡强, 沿流动方向2个涡系相互干渉, 分离涡与相邻叶栅脱落涡逐渐合并。高阶模态相邻涡核距离缩小, 表明高阶模态捕捉到流场更小尺度旋涡, 结构之间的相互影响也更加复杂, 并主要集中在尾缘脱落涡区域。
图 9所示为前6阶模态系数功率谱密度图。可以看出, 相邻模态频率特性基本一致, 表明相邻模态为耦合模态。各阶模态系数均包含多个频率, 无法获得单频模态, 尽管各阶模态主特征频率明显, 且主特征频率与非定常流场分析一致, 但对叶栅附面层分离所产生的旋涡结构形式, 以及旋涡波动频率特征的探索不利。高阶模态频率特性复杂, 使得物理描述混乱, 流动结构难以获得清晰识别, 不利于流动的精细化控制, 而按照能量排序的POD方法也可能会造成能量较小, 且接近主频率的流动成分难以获得。
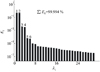 |
图 7 各阶POD模态能量分布图 |
 |
图 8 POD模态云图 |
 |
图 9 POD模态系数功率谱密度图 |
3.2 DMD分解
在标准DMD方法中, 模态按照模态振幅排序, 模态振幅代表该模态对初始快照的贡献率。DMD方法提取的第1阶模态为静态模态, 近似于平均流场, 其余模态包括共轭模态和漂移模态。图 10给出了模态数与损失函数的关系, 可以看出前9个模态(实心点)已经使得损失函数足够小。
由于POD选取了6阶模态, 作为对比, DMD选取6阶模态, 即前9个模态。各阶模态的振幅与频率关系如图 11所示, 前9个模态包括一个静态模态, 3个共轭模态(2~3, 6~7, 8~9)和2个漂移模态(4, 5)。
从图 12的特征值分布图可以看出, DMD所选取的模态均位于单位圆上或单位圆内, 为稳定模态或周期模态, 其余模态基本位于单位圆上, 表明此时的流动处于稳定阶段。
模态的增长率和频率如表 2所示。由于第1阶静态模态与均匀流场相似, 增长率和频率均为零。第2和第5阶共轭模态为倍频模态, 频率与POD模态系数主特征频率一致, 这2阶模态获得了流动的主要特征结构。第4和第5阶为漂移模态, 即瞬时数值模态, 这些模态的作用是为了补偿除主要动态模态外, 对快照重构的残差。第6阶共轭模态衰减率较大, 该模态主要来源于周期交界面引起的流场数值震荡、数据传递误差以及DMD截断误差, 属于伪模态, 由于DMD方法对数值噪声很敏感, 导致捕捉了该模态。
图 13给出了DMD第2、第5和第6阶模态实部云图, 虚部与实部仅存在一定的相位差异[16], 所以并未给出。可以看出, 流动的主要结构, 即吸力面分离涡和尾缘脱落涡结构均获得, 相干结构与POD第1和第3阶模态一致。DMD第6阶模态并非主要结构, 属于为了获得高频模态需要剔除振幅较大的伪模态。
按照振幅排序的标准DMD方法并没有捕捉到高频模态, 导致无法用有限的模态数获得流动的主要相干结构, 这是该方法的缺陷, 也是相关研究者持续关注的难点, 并提出多种模态排序方法[12]。不同排序方法对同一问题的适应性并非本文研究重点, DMD模态选取准则的不统一, 也是制约该方法应用的因素。
 |
图 10 DMD模态数与损失函数的关系 |
 |
图 11 DMD模态振幅与频率关系 |
 |
图 12 DMD模态特征值分布 |
DMD模态增长率和频率
 |
图 13 DMD模态云图 |
3.3 SPOD分解
SPOD方法有类似于PSD的数据表示方式, 如图 14所示。每个频率下的特征值均按照能级降序排列, 同时为了研究能量随频率的变化规律, 将同一能级特征值绘制曲线, 称为SPOD特征值谱图, 图中特征值使用流场总能量归一化。从图中可以看出, 在特定频率区间, 如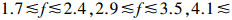
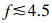 和
和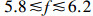 , 第1阶模态能量明显高于第2阶模态, 表明第1阶模态的物理结构占主导地位, 该现象称为流动的低秩行为[13], 而POD无法捕捉该现象。
, 第1阶模态能量明显高于第2阶模态, 表明第1阶模态的物理结构占主导地位, 该现象称为流动的低秩行为[13], 而POD无法捕捉该现象。
低秩行为第1、第3和第4频率区间的峰值频率与POD模态系数主特征频率一致, 且峰值频率对应的能量总和随着频率的增加而降低, 这也符合POD模态能量与频率的关系, 而第2频率区间因为与相邻区间能量差距较大, 隐藏在了POD主模态中。
为方便与POD对比, 给出第1、第3和第4峰值频率对应的SPOD单频模态云图。如图 15所示, SPOD第1阶模态与POD模态结构相似, 形态变化基本一致, 表明2种方法均能够捕捉到流场主要特征结构, 但是SPOD能够体现准确的频率特性。因为SPOD模态为单频时空模态, 相比于空间多频率耦合POD模态, 其获得的相干结构为真实的物理结构, 间接表明了POD模态分解方法提取流场主要相干结构的有效性。SPOD第2阶模态表现出不同于第1阶模态的行为, 且不同频率下均与低频主导模态形态基本一致, 仅存在细微的相位差异, 这表明叶栅非定常流动中可能存在多种不同性质的流动。SPOD方法能够提供更丰富的动态结构, 在模态分析方面具有明显优势。
 |
图 14 SPOD特征值谱图 |
 |
图 15 SPOD模态云图 |
4 结论
本文分别将POD、DMD和SPOD方法应用于高负荷压气机叶栅非定常分离流动分析, 对比了3种模态分解方法时空相干结构辨识差异性, 得到结论如下:
1) POD方法将模态按照能量排序, 高效提取流场主要空间结构, 但模态系数存在多频率耦合, 导致无法获得单频结构, 不利于研究压气机叶栅周期性流动的主导模态特征。高阶模态能够获得高频流动结构, 但数值噪声较多, 流动动力学特性不清晰。
2) 相比于POD模态能量排序方法, 按照振幅排序的标准DMD方法, 能够获得叶栅流动的时空单频动态相干结构, 及其增长率和频率, 还可以判断所提取模态的稳定性。但是该方法捕捉到大衰减率的大振幅次优模态, 并未获得压气机叶栅流场的高频结构, 导致无法用有限的模态数得到流动主导相干特征。
3) SPOD方法获得了叶栅流场的时空单频模态, 且不存在模态筛选问题, 而谱估计方法的使用降低了对数值噪声的敏感性, 提高了模态分解的鲁棒性。该方法能够获得压气机叶栅流场的低秩行为, 提供更丰富的动态结构, 有助于增强对叶栅流动机理的理解, 为进一步实施流动控制提供理论基础。同时表明, 对于压气机叶栅非定常分离流动系统进行模态分析时, SPOD方法具有明显优势。
References
- Dowell E H, Hall K C. Modeling of Fluid Structure Interaction[J]. Annual Review of Fluid Mechanics, 2001, 33(1):445–490 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Li J C, Cai J S, Qu K. Adjoint-Based Two-Step Optimization Method Using Proper Orthogonal Decomposition and Domain Decomposition[J]. AIAA Journal, 2018, 56(3):1133–1145 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Brunton S L, Noack B R. Closed-Loop Turbulence Control:Progress and Challenges[J]. Applied Mechanics Reviews, 2015, 67(5): 050801 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Sirovich L. Turbulence and the Dynamics of Coherent Structures I. Coherent Structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561–571 [Article] [Google Scholar]
- Wang Yangang, Chen Junxun, Xian Songchuan. Analysis of Square Cylinder Unsteady Flow at Low Reynolds Number with POD Method[J]. Journal of Northwestern Polytechnical University, 2014, 32(4): 612–617 [Article] [Article] (in Chinese) [Google Scholar]
- Seidel J, Siegel S, Cohen K, et al. POD Based Separation Control on the NACA0015 Airfoil[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, 2005 [Google Scholar]
- Wang Y G, Li Y, Chen J X. Analysis of the Unsteady Flow in Compressor Cascade with POD Method[C]//ASME Turbo Expo: Turbine Technical Conference and Exposition, 2016 [Google Scholar]
- Schmid P J. Dynamic Mode Decomposition of Numerical and Experimental Data[J]. Journal of Fluid Mechanics, 2010, 656(10): 5–28 [Article] [Google Scholar]
- Kou J Q, Zhang W W, Liu Y L, et al. The Lowest Reynolds Number of Vortex-induced Vibrations[J]. Physics of Fluids, 2017, 29(4): 041701 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Mariappan S, Gardner A D, Richter K, et al. Analysis of Dynamic Stall Using Dynamic Mode Decomposition Technique[J]. AIAA Journal, 2013, 52(11): 2427–2439 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Kou Jiaqing, Zhang Weiwei, Gao Chuanqiang. Modal Analysis of Transonic Buffet Based on POD and DMD Method[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2679–2689 [Article] (in Chinese) [Google Scholar]
- Kou Jiaqing, Zhang Weiwei. Dynamic Mode Decomposition and its Applications in Fluid Dynamics[J]. Acta Aerodynamica Sinica, 2018, 36(2): 163–179 [Article] (in Chinese) [Google Scholar]
- Aaron T, Schmidt O T, Tim C. Spectral Proper Orthogonal Decomposition and its Relationship to Dynamic Mode Decomposition and Resolvent Analysis[J]. Journal of Fluid Mechanics, 2018, 847: 821–867 [Article] [CrossRef] [Google Scholar]
- Abreu L I, Cavalieri A V G, Wolf W R. Coherent Hydrodynamic Waves and Trailing-Edge Noise[C]//23rd AIAA/CEAS Aeroacoustics Conference, 2017 [Google Scholar]
- Araya D, Dabiri J. Transition to Bluff Body Dynamics in the Wake of Vertical Axis Turbines[J]. Journal of Fluid Mechanics, 2017, 813(7): 346–381 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Chen K K, Tu J H, Rowley C W. Variants of Dynamic Mode Decomposition:Boundary Condation, Koopman, and Fourier Analysis[J]. Journal of Nonlinear Science, 2012, 22(6): 887–915 [Article] [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
All Tables
All Figures
 |
图 1 叶栅几何结构示意图 |
| In the text | |
 |
图 2 网格拓扑图 |
| In the text | |
 |
图 3 无量纲压力分布图 |
| In the text | |
 |
图 4 全局流场瞬时涡量图 |
| In the text | |
 |
图 5 局部流场瞬时涡量图 |
| In the text | |
 |
图 6 叶表静压力积分功率谱密度图 |
| In the text | |
 |
图 7 各阶POD模态能量分布图 |
| In the text | |
 |
图 8 POD模态云图 |
| In the text | |
 |
图 9 POD模态系数功率谱密度图 |
| In the text | |
 |
图 10 DMD模态数与损失函数的关系 |
| In the text | |
 |
图 11 DMD模态振幅与频率关系 |
| In the text | |
 |
图 12 DMD模态特征值分布 |
| In the text | |
 |
图 13 DMD模态云图 |
| In the text | |
 |
图 14 SPOD特征值谱图 |
| In the text | |
 |
图 15 SPOD模态云图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


