| Issue |
JNWPU
Volume 38, Number 6, December 2020
|
|
|---|---|---|
| Page(s) | 1210 - 1217 | |
| DOI | https://doi.org/10.1051/jnwpu/20203861210 | |
| Published online | 02 February 2021 | |
Research on Fault Detection Method of FADS System
FADS系统故障诊断方法研究
School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
Received:
4
April
2020
In order to solve the fault detection problem of flush air data sensing (FADS), an advanced airborne sensor, a new method is proposed in this paper. First, the high-precision FADS model is established on the basis of the database obtained from the CFD software and aerodynamics knowledge. Then, the distribution characteristics of each group of signals under fault condition are derived through strict formulas. Meanwhile, the threshold of alarm times is designed with statistical knowledge. For verifying the effectiveness of the newly proposed method, a comparison with other two widely adopted methods, including the methods based on parity equation and Chi-square χ2 distribution, is conducted under different measurement noise. Simulation results show that the proposed fault detection method for FADS possess higher accuracy and stronger anti-interference.
摘要
为解决一种先进的新型机载传感器——嵌入式大气数据传感器(flush air data sensing,FADS)的故障诊断问题,提出了一种新的方法。基于CFD软件和空气动力学知识获得数据库并建立高精度FADS模型。以系统数学模型为基础,经过严格的公式推导得到故障情况下各组信号的分布特点。为了降低虚警率,基于统计学知识设计了告警次数阈值。为了验证新提出方法的有效性,在不同方差的测量噪声情况下分别将所提方法与以往该领域中被广泛采纳的基于奇偶方程和卡方χ2分布的2种传统方法进行了对比与分析。结果表明,与以往FADS系统的故障诊断方法相比,新提出方法具有更高的诊断精度和更强的抗干扰性。
Key words: fault detection / flush air data sensing(FADS) / parity equation / Chi-square χ2 distribution / simulatio
关键字 : 嵌入式大气数据传感器 / 故障诊断 / 奇偶方程 / 卡方χ2分布
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
在飞行过程中, 机载传感器的测量结果是飞行员了解飞机状态的重要渠道, 传感器的测量精度将直接关乎到整个飞行过程的安全。
在众多传感器中, 大气数据传感器占据了重要部分, 传统的探针式大气数据传感器以空速管为基础, 配合迎角传感器、侧滑角传感器等得到迎角和侧滑角等状态量。但是考虑到现代飞行器的飞行包线越来越大, 复杂的飞行环境极易造成探针式大气数据传感器损坏, 而且外露的探针也不适用于追求隐身效果的现代战机。值得一提的是, 在2018年和2019年印尼狮航和埃塞俄比亚航空的2架波音737 MAX型客机先后坠毁, 后来的调查显示事故主要原因正是迎角传感器出现了故障[1]。因此, 包括美国, 英国等很多国家均开始进行嵌入式大气数据传感器的相关研究。
和传统的大气数据传感器不同, FADS系统主要利用嵌入在机体内的压力传感器对迎角、侧滑角等状态量进行推导, 可以有效地克服传统探针式传感器的缺点和不足[2-4]。
值得注意的是, 虽然相较于传统的大气数据传感器, FADS系统在稳定性和可靠性上确实得到了大幅提升, 但是因为其主要运用在X-43A、X-33和X-31等高超声速飞行器上, 飞行过程中过高的表面温度可能会造成系统发生故障, 影响飞行员对飞机状态的判断, 从而构成安全隐患。所以, 如何有效及时地检测出FADS系统的故障类型就显得尤为重要。参考文献[5]通过计算各测压孔的残差, 然后总结其分布特征, 利用卡方检测方法实现对FADS系统的故障检测。此方法在测量噪声方差不大时有效, 但是一旦方差增大, 测量精度则会急剧下降。文献[6]以FADS系统算法中三点法的冗余性为基础, 结合粗糙集的知识, 提出了基于奇偶方程的FADS系统故障检测方法, 但是不足的是, 此方法同样受制于噪声方差。此外, 国内外学者们基于神经网络算法先后提出多种FADS系统故障检测方法, 比如, 单一神经网络算法[7]、分层神经网络算法[8]、单一径向基神经网络算法[9], 但是这些方法都需要大量数据支撑, 一旦数据不充分或者不真实, 检测精度就会受到很大影响, 且由训练数据过多造成的大计算量问题也难以得到解决。
经过对相关文献梳理后可以发现, FADS系统的故障诊断问题仍未得到很好地解决, 一种简单有效、可以运用于工程实际的方法是亟需的。为了解决这个问题, 本文以FADS系统模型为基础, 提出一种新的FADS系统故障检测方法。
本文主要包括以下创新点:
1) 以往的相关文献资料仅对FADS系统的建模方法进行简要介绍, 但是很少公布有关的具体空气动力学数据。本文将得到的一系列不同条件下的数据进行作图展示, 为后续其他相关学者的研究提供了参考。
2) 为了切实地解决FADS系统故障诊断问题, 本文从系统模型出发, 在充分考虑了系统的特殊性后, 设计了一种可用于工程实际的可靠方法。
3) 为了进一步验证本文提出方法的有效性, 本文将其与基于奇偶方程和卡方χ2分布等2种传统方法在不同方差的噪声情况下进行了深入的对比与分析。
1 问题描述
FADS系统是一种先进的大气数据测量系统, 安装在飞行器头部前端周线上, 主要通过压力传感器测量飞行器头部表面的压力分布, 然后利用解算算法获得所需要的大气参数。考虑到现有资料对X-33飞行器上的FADS系统研究最为成熟, 因此本文主要基于此系统开展研究[10]。
X-33上FADS系统主要由机头附近表面的6个测压孔组成, 每个测压孔中都安置有压力传感器, 测压孔的排布方式如图 1所示。
由空气动力学知识可以知道, 在X-33的飞行过程中, 其表面压力数学模型为
式中: pi表示第i个测压孔的压力值; qc表示动压; p∞表示静压; ε表示修正系数; θi表示来流入射角(即第i点的曲面法线方向和速度矢量之间的夹角), 可通过(2)式计算得到
式中, ϕi和λi分别表示测压孔的圆周角和圆锥角, 具体数值如表 1所示; α, β表示迎角和侧滑角。
X-33 FADS系统中迎角解算算法采用的是NASA提出的“三点法”[10], 即从纵向分布的1, 3, 5, 6号孔中选择3个测压孔的测量压强值pi, pj, pk, 将其带入(1)式, 联立方程可得
式中, θi, θj和θk表示3个测压孔的来流入射角。
整理(3)式可得
式中
将(2)式代入(4)式, 得到
式中
解(5)式, 得到迎角的计算公式
值得注意的是, 之所以没有利用2号孔和4号孔的原因是这2个孔呈纵向分布, 当迎角改变时, 其压强值并不会出现明显的变化。也就是说这2个孔的压强并不能很好地反映出迎角的改变, 会很大程度上影响测量精度。
可以看到, 运用此方法得到的迎角解析值一共有C43=4种, 分别是由(1, 3, 5)号孔组合得到的α1, (1, 3, 6)号孔组合得到的α2, (1, 5, 6)号孔组合得到的α3和(3, 5, 6)号孔组合得到的α4。为了尽可能地消除各测压孔的测量误差对最终计算结果的影响, 取4组迎角值的平均值作为最终迎角解析值
在对所有组合的侧滑角解析值进行数据分析后, 发现(2, 3, 5)、(2, 4, 6)和(3, 4, 5)3个组合得出的结果β1, β2, β3与实际值最为接近, 精度较高。因此, 借鉴迎角解析值的方法, 取其平均值作为最终的侧滑角解析值β。
为了驱动已建立的模型, 本文利用CFD软件和空气动力学知识计算得到不同条件下的数据, 如图 2和图 3所示。
 |
图1 X-33的FADS系统测压孔布局 |
各测压孔的圆周角与圆锥角
 |
图2 飞行高度10 000 m时的空气动力学数据 |
 |
图3 飞行高度12 000 m时的空气动力学数据 |
2 故障检测系统设计
当测压孔发生故障时, 解析得到的4组迎角和3组侧滑角必然也会偏离实际值, 并且各组值之间会存在一定的大小关系, 值得注意的是, 当不同测压孔发生故障时, 各组值之间的大小关系是不同的。因此, 笔者拟利用此特性设计FADS系统的故障诊断方法。
本文只针对单测压孔故障情况进行研究, 不对多测压孔同时发生故障情况进行讨论, 为了方便计算推导, 本文设定当测压孔发生故障时, 认定其完全损坏, 读数为零, 且系统噪声干扰仅加在测压孔上, 除此之外不添加别的干扰。为了便于分析, 将6个孔按照纵向和横向分布分别进行研究。
2.1 故障检测原理
2.1.1 纵向分布的测压孔发生故障
考虑到FADS系统主要运用于高超声速飞行器, 很少有做大机动的需求, 因此本文仅针对迎角小于45°的情况进行研究, (6)式可简化为
假设1号孔发生故障, 就α1而言, (9)式中A可写成如下形式
考虑到λ1=λ5=20°, p1=0, λ3=0所以(10)可简化为A1, 3, 5=p5sin220°。
同理
与α1类似
由数学知识可以知道, (9)式中的反正切函数为单调递增函数, 所以要想判断α1和α2的大小关系, 只需要对 和
和 进行做差比较即可。
进行做差比较即可。
根据空气动力学知识可知, 当气流分布在机头时, 越接近机头压强值越大, 即p3>p5>p6。
对(14)式分析可得 , 因此α1 < α2。
, 因此α1 < α2。
其余情况均与此类似, 在此不做赘述。
在对所有情况进行推导分析后, 可以得到下面的分布规律。
1) 当1号孔故障时: α3>α2>α1>α4
2) 当3号孔故障时:α4>α2>α1>α3
3) 当5号孔故障时:α4>α3>α2>α1
4) 当6号孔故障时:α4>α1>α3>α2
对FADS系统进行故障诊断时, 只需要将4组迎角解析值之间的大小关系与上述分布特征进行匹配, 便可以确定具体故障孔。
2.1.2 横向分布的测压孔发生故障
与2.1.1节一样, 当2号孔和4号孔发生故障时, 3组侧滑角解析值同样会呈现以下的分布特征。
1) 当2号孔故障时: β1>β3>β2
2) 当4号孔故障时:β2>β1>β3
2.2 告警次数阈值的确定
由于测量噪声的存在, 即使所有的测压孔都不发生故障, 各组迎角和侧滑角也会上下波动, 之间仍存在着大小关系, 若用2.1节中的分布规律进行故障判断, 必然会导致误检测。为了解决此问题, 本文通过设置告警次数阈值M以减少误警率。
假设测量孔存在均值为0, 标准差为δ的正态分布干扰噪声。以迎角为例, 当系统正常工作时, 4组迎角解析值是围绕着实际值随机波动的, 任意2组解析值之间大小关系的概率值均为0.5, 比如P(α1>α2)=P(α2>α1)=0.5, 4组值同时满足某种特定大小关系概率为0.125。考虑到0.1255≈0.003%近似为0, 因此本文选择次数门限值M等于5, 即认为系统在连续采样5次时, 4组迎角解析值都出现同一种大小关系的概率接近于0, 如若真的连续出现5次甚至更多则可以断定系统出现故障。
3 仿真验证
为了验证本文所提方法有效性, 采用下面2种情况对算法进行测试。
1) 1号孔故障, 各测压孔上的测量噪声呈均值为0, 方差为2002 Pa2的正态分布;
2) 1号孔故障, 各测压孔上的测量噪声呈均值为0, 方差为4002 Pa2的正态分布。
设置测量状态点飞行高度11 000 m, 飞行速度350 m/s, 实际迎角-5°, 实际侧滑角0°, 仿真时间10 s, 采样频率50 Hz。
·1号孔故障, 噪声方差2002 Pa2
从图 4可以看到, 前5 s各测压孔的压强值均保持正常, 因为是左右对称分布, 所以2号孔和4号孔的值是近似重合的, 只是由于随机测量噪声的存在而稍有不同。设置系统在第5秒时1号孔发生故障, 压强值变为0, 其余测压孔仍保持正常工作。
因为在前5 s内FADS系统保持正常工作, 所以从图 5中可以看到, 各组合得到的迎角值均围绕着实际值在合理范围内波动, 虽出现4组解析值大小不一的情况, 但是连续出现的次数都不高于告警次数阈值。第5秒时1号孔发生故障, α1、α2和α3出现异常, 而因为与1号孔无关, 所以α4仍保持正常, 可以看到此时α3>α2>α1>α4且连续出现的次数超过告警次数阈值, 与2.1节的分布特征进行比对, 可以准确地判断在第5秒时1号孔发生了故障, 这与实际情况是一致的, 方法有效。
·1号孔故障, 噪声方差4002Pa2
为了进一步验证此方法在不同方差情况下的可行性, 将上例中的噪声方差增加至4002 Pa2, 其余条件保持不变。
从图 6可以看到, 前5秒各测压孔的压强值均保持正常, 第5秒时1号孔发生故障, 压强值变为0, 其余测压孔仍保持正常工作。相较于上例, 因为噪声方差的增加, 图 6中各信号的波动幅度要明显大于图 4。
从图 7可以看到, 前5秒内各组合得到的迎角解析值均是正常的, 第5秒时由于1号孔出现故障, α3>α2>α1>α4且连续出现的次数超过告警次数阈值, 与2.1节的分布特征进行比对可知, 第5秒时1号孔发生了故障, 这与实际情况是一致的, 方法有效。
 |
图4 各测压孔压强值 |
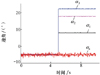 |
图5 1号孔发生故障时各迎角解析值 |
 |
图6 各测压孔压强值 |
 |
图7 1号孔发生故障时各迎角解析值 |
4 比较与分析
为了进一步验证本文提出的方法的可行性,在相同的仿真情况下将其与FADS系统故障诊断中运用最为广泛的奇偶方程法[6]和卡方χ2分布法[5]进行比较分析。
4.1 奇偶方程法
4.1.1 工作原理
就FADS而言,若系统正常,那么(1)式将严格成立,化简可得系统奇偶方程[6]
由于在测量过程中存在噪声干扰,奇偶方程无法严格等于零。为了解决这个问题,研究人员设定经验门限值N,若(16)式成立也可以认为系统正常。
此方法的主要工作流程是将6个孔的压强值和来流入射角按照排列组合方式3个1组,代入(16)式,若不等式成立则相应组合的奇偶方程检测值置为0,反之则记为1,然后与文献[6]中的标准故障向量表进行比较,确定故障类型。为了减小计算量,文献[6]利用粗糙集知识将C63=20种情况简化成(1, 2, 4),(1, 4, 5),(2, 3, 6),(2, 4, 5),(2, 4, 6),(2, 5, 6),(3, 4, 5),(3, 4, 6),(3, 5, 6),(4, 5, 6)共10种情况。比如说当1号孔发生故障时,只要是不涉及此孔的奇偶方程值均会在0附近,而与此孔有关的奇偶方程值则会远离0,选择一个合适的经验门限值便可以将这2种情况分开,从而得到1号孔故障的标准故障向量表(1, 1, 0, 0, 0, 0, 0, 0, 0, 0)。
4.1.2 故障诊断结果
·1号孔故障,方差为2002 Pa2
因组合情况过多,在此仅对(1, 4, 5)和(2, 3, 6)组合做具体分析。从图 8可以看到,前5秒内2种组合得到的奇偶方程值均在零附近,但是当第5秒1号孔发生故障时,(1, 4, 5)组合的数值出现异常,而因为(2, 3, 6)组合与1号孔无关,故而其数值不受影响。为了将这2种组合计算出的奇偶方程值区分开,可以选择合适的门限值如1 000。其余组合情况与此类似,由此可以得出整个10种组合的奇偶方程检测值:前5秒为(0, 0, 0, 0, 0, 0, 0, 0, 0, 0),随后变成(1, 1, 0, 0, 0, 0, 0, 0, 0, 0),与文献[6]中的标准故障向量表匹配可以得出结论,系统第5秒时1号孔发生故障,方法有效。
·1号孔故障,方差为4002 Pa2
与上述情况唯一不同的是,因为测压孔上的噪声方差增加至4002 Pa2,奇偶方程值上下波动的幅度增加。从图 9可以看出,后5秒2种组合的数值已经完全混合在一起,无法选择一个经验门限值将这2种组合的奇偶方程检测值分别置为1和0,此方法失效。
 |
图8 (1, 4, 5)和(2, 3, 6)组合的奇偶方程值 |
 |
图9 (1, 4, 5)和(2, 3, 6)两种组合的奇偶方程值 |
4.2 卡方χ2分布法
4.2.1 工作原理
本方法的依据原理是在故障与非故障情形下,测压点压强与由压力模型推导出的压强之间的残差在统计特性上是不同的[5]。就本例而言,主要工作流程可以分为2步:①根据1, 3, 5和6号孔残差的卡方和是否大于7.78以判断系统是否发生了故障;②逐个排除测压孔并计算剩余测压孔的卡方值以明确具体的故障孔。
值得注意的是,之所以选择7.78是因为由χ2(4)特性可知,一旦卡方和大于7.78,那么系统出现故障的概率是90%,近似认为发生故障。
4.2.2 故障诊断结果
1号孔故障,方差为2002 Pa2
从图 10a)可以看到,卡方和在前5秒内小于7.78,系统正常,随后数值增加,系统发生故障。为了确定具体的故障孔,分别计算(3, 5, 6),(1, 5, 6),(1, 3, 6)和(1, 3, 5)号孔组合的卡方和来逐个排除1, 3, 5和6号孔,结果如图 10b)所示,图 10c)的柱形图用来更清晰地显示后5秒内各组合的情况。可以看到,在剔除了1号孔后,剩余3个孔的卡方和回归正常,出现故障的概率仅为6.0%,而与1号孔有关的所有组合故障率都很高。因此,此方法检测出1号孔发生故障,方法有效。
·1号孔故障,方差为4002 Pa2
从图 11可以看到,在噪声方差为4002 Pa2时,此方法仍可以诊断出系统在第5秒时发生故障。但是,卡方和的波动幅度较图 10有明显增大,在剔除了1号孔后的故障率仍高居39.0%,系统无法准确判断出故障孔,此方法失效。
为了进一步分析比较这3种方法在不同噪声条件下的诊断精度,笔者将例子中的方差分别设置为2002, 2502, 3002, 3502, 4002 Pa2,在每种噪声情况下对每个方法进行多次重复测试,统计成功诊断的次数,得到诊断精度,如图 12所示。
可以看到,随着噪声方差的不断增大,本文提出的方法始终能够保持很高的诊断精度,但是奇偶方程法和卡方分布法的诊断精度受到很大影响,诊断精度逐步降低。
 |
图10 噪声方差2002 Pa2时卡方分布诊断结果 |
 |
图11 噪声方差4002 Pa2时卡方分布诊断结果 |
 |
图12 3种方法在不同噪声情况下的诊断精度 |
5 结论
本文针对嵌入式大气数据传感器的故障诊断问题,提出了一种实用的故障诊断方法,结合理论和数值结果分析,可以得出以下结论:
1) 本文提出的算法从系统数学模型出发,深入分析系统故障时冗余信号分布特征,并根据统计学知识确定告警次数阈值,算法流程清晰,有利于工程实际中的应用。
2) 通过为FADS系统注入故障的方式进行数值仿真,验证了本文算法的有效性,指出此方法可适用于不同方差噪声等情况。
3) 通过对比仿真不同方法在不同方差噪声干扰情形下的结果,可知本文提出的方法在干扰比较强的时候仍然拥有最高的故障诊断精度,具备精度高、抗干扰性强的优点。
本文所设计的方法主要针对单测压孔发生故障的情形,未来将会针对多测压孔同时发生故障时的情形开展研究。
References
- Chris Palmer. The Boeing 737 Max Saga:Automating Failure[J]. Engineering, 2020, 6(1): 2-3 [CrossRef] [Google Scholar]
- Liu Yanbin, Xiao Dibo. Trade-Off Design of Measurement Tap Configuration and Solving Model for a Flush Air Data Sensing System[J]. Measurement, 2016, 90: 278-285 [CrossRef] [Google Scholar]
- Jia Qianlei, Hu Jiayue, Zhang Weiguo. A Novel Fault Detection Model Based on Atanassov's Interval-Valued Intuitionistic Fuzzy Sets, Belief Rule Base and Evidential Reasoning[J]. IEEE Access, 2020, 8: 4551-4567 [CrossRef] [Google Scholar]
- Zhang Mingge. Research on Flush Air Data Sensing System in Hypersonic Flight. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014 (in Chinese) [Google Scholar]
- Zhao Lei. Research on Failure Detection and Fault Management Techniques of Flush Air Data Sensing System[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010 (in Chinese) [Google Scholar]
- Guo Yangming, Li Qingdong, Cai Xiaobin, et al. FADS Sensors Fault Detection Based on Parity Equation[J]. Aeronautical Computing Technique, 2010, 40(2): 98-100 (in Chinese) [Google Scholar]
- Rohloff T J, Whitmore S A, Ivan C. Air Data Sensing from Surface Pressure Measurements Using a Neural Network Method[J]. AIAA Journal, 1998, 36(11): 2094-2101 [CrossRef] [Google Scholar]
- Rohloff T J, Whitmore S A, Ivan C. Fault-Tolerant Neural Network Algorithm for Flush Air Data Sensing[J]. Journal of Aircraft, 1999, 36(3): 541-549 [CrossRef] [Google Scholar]
- Ihab Samy, Ian Postlethwaite, Gu D W. Neural-Network-Based Flush Air Data Sensing System Demonstrated on a Mini Air Vehicle[J]. Journal of Aircraft, 2010, 47(1): 18-31 [CrossRef] [Google Scholar]
- Whitmore S A, Cobleigh B R, Haering E A. Design and Calibration of the X-33 Flush Airdata Sensing(FADS) System[R]. NASA/TM-1998-206540 [Google Scholar]
All Tables
All Figures
 |
图1 X-33的FADS系统测压孔布局 |
| In the text | |
 |
图2 飞行高度10 000 m时的空气动力学数据 |
| In the text | |
 |
图3 飞行高度12 000 m时的空气动力学数据 |
| In the text | |
 |
图4 各测压孔压强值 |
| In the text | |
 |
图5 1号孔发生故障时各迎角解析值 |
| In the text | |
 |
图6 各测压孔压强值 |
| In the text | |
 |
图7 1号孔发生故障时各迎角解析值 |
| In the text | |
 |
图8 (1, 4, 5)和(2, 3, 6)组合的奇偶方程值 |
| In the text | |
 |
图9 (1, 4, 5)和(2, 3, 6)两种组合的奇偶方程值 |
| In the text | |
 |
图10 噪声方差2002 Pa2时卡方分布诊断结果 |
| In the text | |
 |
图11 噪声方差4002 Pa2时卡方分布诊断结果 |
| In the text | |
 |
图12 3种方法在不同噪声情况下的诊断精度 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


