| Issue |
JNWPU
Volume 38, Number 6, December 2020
|
|
|---|---|---|
| Page(s) | 1352 - 1360 | |
| DOI | https://doi.org/10.1051/jnwpu/20203861352 | |
| Published online | 02 February 2021 | |
Estimation Method of SAR Doppler Frequency Rate Based on FrFT
一种基于FrFT的SAR多普勒调频率估计方法
Chengdu Technological University, Chengdu 611730, China
Received:
18
April
2020
Due to the problem that the existing Doppler frequency rate estimation method is limited by the estimation accuracy, a novel estimation method of Doppler frequency rate is proposed. The present method searches the frequency rate according to the characteristic of the chirp signal in the FrFT domain. Firstly, dechirp is performed on several strong scattering points extracted from the data domain after pulse compression, and a frequency domain focused image is obtained after FFT. Then the maximum point of each distance unit is extracted. The energy of the maximum point is selected by using the window processing. After that, IFFT is performed and the dechirp conjugate reference function is multiplied by using the selected points. FrFT is performed according to the preset orders. The entropy is used to evaluate whether the order of FRFT is optimal or not. The Doppler frequency rate is calculated by using the optimal order. The simulation and real data are processed and analyzed. The present method can estimate the Doppler frequency rate accurately. A well-focused SAR image is obtained after azimuth matching filtering.
摘要
针对现有多普勒调频率估计方法估计精度有限的问题,提出一种新的估计方法,该方法根据线性调频信号在FrFT域具有明显聚焦的特性实现对调频率的搜索。对从脉压后的数据域提取的若干强散射单元分别进行dechirp处理,进行FFT得到频域聚焦图像。提取各距离单元最大值点并进行加窗处理,然后经IFFT变换到慢时间域与dechirp共轭参考函数相乘,根据设定的阶数进行FrFT处理。通过评估FrFT变换后信号的熵值确定阶数是否达到最优,利用搜索的最优阶数计算出多普勒调频率。在实验数据分析部分,分别利用仿真数据以及实测数据对所提方法进行验证,最终结果分析表明该方法具有很高的估计精度,经过方位匹配滤波后可以得到聚焦良好的SAR图像。
Key words: doppler frequency rate / FrFT / SAR / dechirp
关键字 : 多普勒调频率 / 分数阶傅里叶变换 / SAR / dechirp
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
随着雷达技术的不断进步,人们对雷达的探测能力提出了更高的要求,其中合成孔径雷达(synthetic aperture radar, SAR)具备获取高分辨图像的能力,在军事及民用领域获得了广泛应用[1-2]。然而,随着SAR图像分辨率的提高,对SAR成像所需要的参数精度要求也越高。高分辨通过大的信号带宽及长合成孔径时间获得,运动平台受到自身抖动、气流等影响不可避免引入运动误差[3]。直接利用惯性导航设备往往难以获得较高质量的SAR图像,因此对参数估计算法提出了新的挑战。
众所周知,多普勒调频率作为SAR成像的重要参数决定着SAR图像聚焦的质量。国内外相关学者在多普勒调频率估计方面做了很多工作,其中比较典型的方法包括图像偏移(map drift, MD)、多孔径偏移(multi-aperture map drift, MAMD)、最大对比度、最小熵等方法。MD算法利用相邻孔径的图像偏移估计剩余多普勒调频率的系数,多普勒调频率估计误差受限于多普勒单元间隔[4-6]。MAMD方法通过将全孔径数据分割成多个子孔径,根据多个子孔径数据对高阶系数进行逼近,能够获得高阶相位系数,该方法涉及大量的矩阵运算,算法复杂度较高,同样具备对场景信息过度依赖的缺陷。最大对比度及最小熵均需要根据步长进行多次迭代得到最优估计结果,执行效率较低[7]。
针对上述问题,本文提出一种基于时频分析的多普勒调频率估计方法。常见的时频分析方法包括:STFT、Cohen、WVD变换、FRFT等方法。短时傅里叶变换(short time fourier transform, STFT)利用滑动窗函数对傅里叶变换进行扩展,多分量信号的短时傅里叶变换存在时间分辨率和频率分辨率的矛盾,对使用产生了较大的限制。双线性时频分布中的维格纳分布因其时间-带宽积达到了Heisenberg不确定原理给出的下界,在存在多分量成分时,存在严重的交叉项,影响多普勒调频率估计精度。Cohen虽然在保持自项集中的基础上最大抑制交叉项,但以降低时频分辨率为代价,且其运算量较大。FRFT作为一种新的时频分析工具,在某一方向上可以很好地抑制多分量信号分布的交叉项,并在该方向达到最佳的能量聚集特性。由于子孔径的多普勒调频率可以近似满足线性调频信号特性,根据惯导误差确定FrFT搜索范围。该方法在特显点选取方面与MAMD、WPGA方法类似,相对于MAMD算法,其优势在于:MAMD算法对于场景较为简单,只有若干散射点的情况,在保证相同精度的条件下,计算量较大,而本文提出的方法通过判断FrFT后信号的聚集程度确定多普勒调频率最优,场景中包含若干强散射点即可估计出多普勒调频率,在实验数据分析部分给出了该算法处理数据的结果,仿真及实测数据处理均得到聚焦良好的SAR图像。
1 SAR成像几何模型
雷达发射信号可以表示为[1]
任意目标点(xn, yn)的基带回波信号es(t, τ)可以表示为
式中:
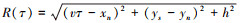 为雷达与目标的瞬时斜距;c为光速;v为飞机速度;t为快时间;τ为慢时间;γ为线性调频信号调频率;λ为信号波长;σp为目标P的后向散射系数;ar(·)为线性调频信号窗函数;aa(·)为方位向窗函数;xn为任意点目标P在斜距平面中的横坐标;yn为目标到雷达在地面投影点的距离;H为雷达相对于目标的高度;xL为合成孔径长度;OL为合成孔径中心;Rs为合成孔径中心与场景中心的距离。SAR成像几何模型如图 1所示。
为雷达与目标的瞬时斜距;c为光速;v为飞机速度;t为快时间;τ为慢时间;γ为线性调频信号调频率;λ为信号波长;σp为目标P的后向散射系数;ar(·)为线性调频信号窗函数;aa(·)为方位向窗函数;xn为任意点目标P在斜距平面中的横坐标;yn为目标到雷达在地面投影点的距离;H为雷达相对于目标的高度;xL为合成孔径长度;OL为合成孔径中心;Rs为合成孔径中心与场景中心的距离。SAR成像几何模型如图 1所示。
 |
图1 SAR成像几何模型 |
回波信号经过脉压、走动校正、距离弯曲补偿、多普勒中心补偿, 将信号在τ=τn处进行泰勒级数展开, 展开后的s(τ)可以表示为
式中:ξk表示泰勒展开第k阶的系数; 多普勒调频项fdr可以表示为
式中:RB为每个距离门对应的斜距;τ表示孔径边缘对应的慢时间。
从(3)式及(4)式可以看出多普勒相位受到以下2个因素影响:1)泰勒级数展开后, (3)式中存在高阶量(τ-τn)k; 2)在斜视情况下, 走动校正将不同距离门的信号补偿到同一距离门内, 造成同一距离门内慢时间方向多普勒调频率不再是固定数值, fdr的变化与积累时间相关, 积累时间越长, 靠近孔径边缘的目标与孔径中心的目标多普勒调频率相差越大, 从而导致fdr估计误差增大。以上2个因素均会导致多普勒调频斜率近似为线性调频信号存在误差, 影响最终估计精度。因此, 本文采用子孔径分割的方法, 将全孔径数据分割成若干子孔径, 每个子孔径积累时间变短。采用孔径分割后, 子孔径内可认为多普勒调频在短时间内为固定值, 将各子孔径估计的多普勒调频率进行拟合, 得到全孔径的多普勒调频率。孔径分割的原则为子孔径内产生的高阶误差及多普勒调频率变化量对多普勒调频率估计的影响可忽略。
2 FrFT域多普勒调频率估计
信号s(t)的分数阶傅里叶变换可以表示为[8]
式中:Bp(t, τ)为分数阶傅里叶变换核, 可以表示为
式中:Aϕ可以表示为
(6) 至(7)式中, ϕ可以表示为
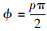 , 表示旋转角度; p表示FrFT阶数; δ(·)为冲击函数; sgn(·)为符号函数。
, 表示旋转角度; p表示FrFT阶数; δ(·)为冲击函数; sgn(·)为符号函数。
Pei等提出了离散型分数阶傅里叶变换的定义[9-12], 由于信号同时包含时域及频域信息, 二者尺度不同, 需要对离散信号进行量纲归一化处理, 经过处理后的信号本身携带信息保持不变。尺度变换根据信号的时域、频域信息选择合适的时宽Δt、采样频率Δf, 确定归一化尺度因子S及归一化间隔Δx, 各变量存在如下关系
式中:Ta为合成孔径时间; FPR为脉冲重复频率。经过尺度变换后的离散采样间隔变为
经过归一化后, 信号s(τ′)可以表示为
将(10)式带入(6)式, 进一步化简, 表示为
式中:ssa(t), ssb(t), ssc(t)分别可写为
将(11)式离散化, 并进行2倍内插, 得到
式中:
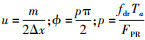 。(13)式中G(u)为
。(13)式中G(u)为
式中, A(Δx)、B(Δx)分别可以表示为
综上所述, 离散型FrFT可以简化为3步[13]:
1) 将信号s(τ′)与chirp信号f0(τ′)=
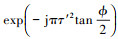 复乘运算, 得到g(τ′);
复乘运算, 得到g(τ′);
2) 将复乘后的信号g(τ′)与另一chirp信号f1(τ′)=exp(jπτ2cscϕ)进行卷积运算, 得到G(τ);
3) 将G(τ)与另一chirp信号f2(τ)=
 进行复乘运算, 得到s(u)。
进行复乘运算, 得到s(u)。
当FrFT匹配阶数κ与信号相匹配时, 即
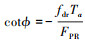 , (13)式可以进一步化简, 得到
, (13)式可以进一步化简, 得到
式中:W(Δx), H(Δx)分别可以表示为
式中, n0表示与目标位置的关系, 具体可以表示为
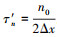 。
。
根据(17)式可得到目标峰值的位置为
通过(18)式可知, 当指定的FrFT阶数与信号多普勒调频率相匹配时, 在
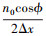 处产生冲击响应。
处产生冲击响应。
当同一距离门出现多个点目标, 并且与FrFT阶数相匹配时, 在FrFT域则会出现多个峰值。在实际场景中, 杂波信号会将目标信号掩盖, 从而影响匹配阶数的估计。本文提出的方法首先根据平台速度等参数计算出的多普勒调频率构的参考函数对选取强散射单元进行dechirp处理, 然后对最强的目标进行加窗, 保留窗内的强点目标, 将窗外的目标及杂波信号置0, 从而达到减少同一距离单元内其他点目标对FrFT域阶数影响的目的。
方位dechirp函数可以表示为[14]
与(3)式进行复乘后, 进行FFT, 得到目标聚焦后的位置, 目标位置与τn关系可以表示为
选取其中的最强点加窗, 将窗宽以外的数据置0, 将信号变换到慢时间域, 乘以sa*, *为共轭。时域表达式可以写为
在雷达运动过程中, 由于受到运动平台速度的变化及惯导设备测量误差等因素的影响, 计算出的多普勒调频率通常存在误差[15]。采用惯导设备计算出的多普勒调频率进行处理难以获得高质量的SAR图像, 因此需要根据存在误差的多普勒调频率进行估计。首先根据(4)式中的运动速度、斜视角、斜距、波长等参数计算出多普勒调频率, 再根据(10)式计算出相应的匹配阶数。计算出的匹配阶数存在一定的误差, 根据惯导误差计算出匹配阶数的误差范围, 从而可以确定FrFT搜索的初始频率及搜索上限、下限。依据惯导计算出的多普勒调频率为fdr_ref, 惯导误差产生的多普勒调频率误差为Δfdr_err, 从而可以确定FrFT匹配阶数κ的搜索范围κ∈[pref-Δperr, pref+Δperr], 式中Δperr表示阶数误差, κ可以进一步表示为
如图 2所示, 分别给出了偏离匹配阶数0.1、偏离匹配阶数-0.1、匹配阶数FrFT结果, 从图 2a)、2b)可以看出能量扩散到多个单元, 图 2c)能量聚焦到1至3个单元内。
 |
图2 不同匹配阶数FrFT结果 |
(16) 式表示阶数匹配时, 在FrFT域位置便会出现冲击响应, 对信号进行不同阶数的FrFT, 得到的响应函数差别较大。阶数失配时, 能量扩散到多个单元内, 阶数匹配时, 能量较为集中。信号熵是评估信号有序程度的参量, 信号的无序程度越高, 对应的熵值越大。该特性刚好可以应用于信号聚焦程度的定性分析, 当FrFT阶数与信号失配时, 信号聚焦特性较差, 信号对应的熵值较大。当FrFT阶数与信号匹配时, 信号聚焦特性较好, 信号对应的熵值较小。首先计算出每个FrFT阶数信号的熵值, 在计算出的熵值中找出最小熵值对应的阶数作为最优解, 如(23)式所示
式中:E表示搜索范围内信号FrFT变换后的信号熵; S0表示信号幅度和; Eopti表示最小熵值。
综上所述, 利用本文提出的多普勒调频率估计方法进行SAR成像可分解为如下步骤:
1) 将全孔径回波数据分割为子孔径, 分别进行脉压、距离徙动校正;
2) 提取出若干强距离单元进行dechirp处理;
3) 找到最大值位置进行加窗;
4) 将信号变换到慢时间域, 乘以dechirp共轭函数;
5) 对信号进行归一化处理;
6) 根据多普勒调频率及普勒调频率误差设定FrFT阶数搜索范围;
7) 对选取的每个距离单元进行有效阶数范围内的FrFT变换, 计算变换后信号的熵值;
8) 根据最小熵对应的阶数计算出相应的多普勒调频率;
9) 根据不同距离单元估计出的多普勒调频率进行误差拟合, 得到子孔径误差;
10) 多个子孔径误差拟合, 得到全孔径运动误差;
11) 运动补偿后进行方位匹配滤波, 得到SAR图像。
具体流程如图 3所示。
 |
图3 基于FrFT多普勒调频率估计的SAR处理流程 |
3 实验数据分析
3.1 仿真数据分析
为了验证本文算法的有效性, 给出了SAR数据的仿真及实测数据处理结果, 仿真参数如表 1所示, 进行了点目标仿真, 仿真实验中雷达工作在条带模式下。
雷达系统参数
点目标回波数据经过脉压及距离徙动校正后, 目标包络在一个距离单元内(见图 4a))。提取目标所在距离单元的实虚部(见图 4b)), 从图中可知, 信号形式满足线性调频信号特性。根据惯导速度、波束斜视角、波长、作用距离可计算出多普勒调频率参考值fdr0。设定惯导速度误差为±2 m/s, 则对应的多普勒调频率误差为Δfdr∈[-2, 2] Hz/s。根据(10)式可得阶数变化误差为Δp∈[-0.004 1, 0.004 1]。根据设定的FrFT搜索阶数对强点目标进行FrFT处理, 得到每个阶数变换结果, 如图 4c)所示, 当阶数与目标信号相匹配, 能量聚焦达到最优, 图 4d)给出了三维图。
 |
图4 仿真结果分析 |
仿真回波增加了83 rad的二次相位误差, 分别采用MD、MAMD算法及本文方法进行估计, 3种方法估计出的相位误差如图 5所示, 与真实的误差进行对比, 可以看出本文提出的方法相位误差估计精度高于MD算法, 与MAMD精度相近。表 2给出了相位误差补偿后点目标的PSLR、ISLR、分辨率。
 |
图5 相位误差估计结果 |
MAMD与本文提出的方法对比
上文的仿真实验给出了信噪比为30 dB的多普勒调频率估计结果, 为了进一步分析本文提出方法对信噪比的适应性, 针对MAMD及本文提出的FrFT方法分别进行了信噪比-10~30 dB的仿真验证, 步进1 dB, 如图 6所示, 横坐标为信噪比变量, 纵坐标为估计的相位误差。从图 6中可以看出, 随着信噪比的增大, 相位误差估计精度逐渐提高, 当信噪比达到某一门限时, 相位误差估计精度的提高变得较为平缓, 考虑到系统设计时会保证SAR成像脉压后信噪比通常大于5 dB, 因此本文提出的方法具有一定的普适性。
 |
图6 MAMD及本文方法在不同信噪比下估计的相位与真值偏差 |
3.2 实测数据分析
为了进一步说明FrFT多普勒调频率估计方法的有效性, 采用机载挂飞数据进行验证, 该雷达工作于X波段, 信号带宽为600 MHz, 飞行速度为150 m/s, 作用距离为15 km, 斜视角为40°。方位积累点数为16 384, 全孔径分割成16个子孔径, 每个子孔径重叠部分数据。
采用本文提出的方法得到估计的多普勒调频率进行全孔径成像。为了体现该方法在多普勒调频率估计方面的有效性, 同时也采用MD、MAMD算法对同一块数据进行了处理, 子孔径长度与FrFT方法相同, MD及MAMD迭代次数为2次。图 7a)~7c)分别给出了MD、MAMD迭代2次估计出的相位误差、FrFT迭代5次估计出的相位误差。
 |
图7 MD、MAMD及FrFT估计出的相位误差 |
全孔径SAR图像如图 8所示, 为了进一步说明相位误差对成像的影响, 从图 8中选取A、B 2块小的区域进行对比。图 9a)为A区MD方法成像放大结果, 图 9b)为A区MAMD方法成像放大结果, 图 9c)为A区FrFT方法成像放大结果。图 10a)为B区MD方法成像放大结果, 图 10b)为B区MAMD方法成像放大结果, 图 10c)为B区FrFT方法成像放大结果。在A区选取一个孤立点目标P, 对该点目标FrFT结果、峰值旁瓣比(PSLR)进行分析。
 |
图8 FRFT估计多普勒调频率成像结果 |
 |
图9 A区图像不同方法处理结果 |
 |
图10 B区图像不同方法处理结果 |
图 11给出了P点FrFT变换结果, 搜索范围为6.92~1.03, 从图中可知在p=0.975 5达到最优。
 |
图11 P点FrFT结果 |
图 12给出了P点3种方法的PSLR对比, 表 2给出了PSLR、ISLR及分辨率对比, 从对比结果可以看出, 本文提出的方法PSLR优于MD算法, 与MAMD的处理结果相近。
 |
图12 MD、MAMD及FrFT方法P点方位PSLR对比 |
3.3 运算复杂度分析
根据上述数据处理结果可以看出, 本文提出的方法在估计精度上优于MD算法, MD算法将每个孔径分割成2个子孔径, 只能解算出2阶相位误差, 而MAMD算法将孔径分割成N个子孔径, 将N个子孔径分别进行互相关, 得到了N个系数, 因此可以解算出N阶的相位误差, 但MAMD算法中存在矩阵求逆, 导致该算法的应用性受到限制。本文提出的利用FrFT算法对多普勒调频率进行估计, 运算中涉及到FFT运算、复乘运算、熵值运算, 其中熵值运算为1维熵值计算, 通过对比分析, MAMD算法运算复杂度高于本文提出的方法, 具体分析如表 3所示。
MAMD及FrFT方法运算复杂度对比
以孔径点数M点为例, 强点个数设为N, 迭代次数设为m, MAMD分割孔径数目为P。
4 结论
本文提出一种基于FrFT的SAR成像多普勒调频率估计方法, 该方法利用FrFT对线性调频信号在时频域能量聚焦性的特点搜索多普勒调频率对应的FrFT匹配阶数, 考虑到高阶误差、大斜视SAR成像对FrFT的影响, 本文采用孔径分割的方法减小长积累时间对多普勒调频变化的影响。采用FrFT域的熵值评估各匹配阶数的聚焦程度, 当阶数与信号多普勒调频率失配时, 信号熵较大, 当阶数与信号多普勒调频率匹配时, 信号熵较小。将各个子孔径估计出的多普勒调频率误差进行拟合, 将全孔径的运动误差补偿到回波数据, 方位匹配滤波后得到聚焦良好的SAR图像, 实验数据分析表明该方法在多普勒调频率估计具有较高的精度。
References
- Bao Zheng, Ying Mengdao, Wang Tong. Radar Imaging Technology[M]. Beijing: Electronic Industry Publication, 2005 (in Chinese) [Google Scholar]
- Tang Yu, Xing Mengdao, Bao Zheng, et al. Wavefront Curvature Compensation Based on Overlapped Subaperture Polar Format Algorithm[J]. Acta Electronica Sinica, 2008, 36 (6): 1108– 1113 [Article] (in Chinese) [Google Scholar]
- Mei Haiwen, Meng Ziqiang, Li Yachao, et al. Airborne Bistatic Forward-Looking SAR Using the Polynomial NCS Algorithm[J]. IEEE Sensors Letters, 2018, 2 (3): 58– 61 [Article] [Google Scholar]
- Wahl D E, Eichel P H, Ghiglia D C, et al. Phase Gradient Autofocus-a Robust Tool for High Resolution Phase Correction[J]. IEEE Trans on AES, 1994, 30 (3): 827– 835 [Article] [Google Scholar]
- Lei Ran, Zheng Liu, Tao Li. Extension of Map-Drift Algorithm for Highly Squinted SAR Autofocus[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10 (9): 4032– 4044 [Article] [CrossRef] [Google Scholar]
- Ye W, Yeo T S, Bao Z. Weighted Least-Squares Estimation of Phase Errors for SAR/ISAR Autofocus[J]. IEEE Trans on Groscience and Remote Sensing, 1999, 37 (5): 2487– 2494 [Article] [CrossRef] [Google Scholar]
- THOMAS Kragh J, Alaa Kharbouch A. Monotonic Iterative Algorithm for Minimum-Entropy Autofocus[C]//IEEE International Conference on Image Processing, Atlanta. 2006: 645–648 [Google Scholar]
- Haldun M, Orhan A, Alper M, et al. Digital Computation of the Fractional Fourier Transform[J]. IEEE Trans on Signal Processing, 1996, 44 (9): 2141– 2150 [Article] [CrossRef] [Google Scholar]
- Cui Jian, Li Zhaohui, Li Qihu, Strong Scattering Targets Separation Based on Fractional Fourier Transformation in Pulse-to-Pulse Coherent Acoustical Doppler Current Profilers[J]. IEEE Journal of Oceanic Engineering, 2019, 44 (2): 466– 480 [Article] [CrossRef] [Google Scholar]
- Lu Jian, Yang Jian, Liu Xinghai. Moving Ground Target Detection with Main-Lobe Jamming Based on Fractional Fourier Transform and Differential Cancellation[J]. IEEE Sensors Journal, 2019, 19 (6): 2275– 2286 [Article] [Google Scholar]
- Tao R, Li Y L, Wang Y. Short-Time Fractional Fourier Transform and Its Applications[J]. IEEE Trans on Signal Processing, 2010, 58 (5): 2568– 2580 [Article] [CrossRef] [Google Scholar]
- Luo Yiran, Yu Chunyang, Chen Shaohua. A Novel Doppler Rate Estimator Based on Fractional Fourier Transform for High-Dynamic GNSS Signal[J]. IEEE Access, 2019, 7 (5): 29575– 29595 [Article] [CrossRef] [Google Scholar]
- Xu Liyun, Zhang Feng, Tao Ran. Fractional Spectral Analysis of Randomly Sampled Signals and Applicationsxy1 IEEE Trans on Instrumentation and Measurement, 2017, 66 (11): 2869– 2881 [Article] [CrossRef] [Google Scholar]
- An Hongyang, Wu Junjie, Sun Zhichao. A 2-D Nonlinear Chirp Scaling Algorithm for High Squint Geo Sar Imaging Based on Optimal Azimuth Polynomial Compensation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10 (12): 5724– 5735 [Article] [CrossRef] [Google Scholar]
- Carrara W G, Goodman R S, Majewski R M. Spotlight Synthetic Aperture Radar-Signal Processing and Algorithms[M]. Boston, MA: Artech House, 1995 [Google Scholar]
All Tables
All Figures
 |
图1 SAR成像几何模型 |
| In the text | |
 |
图2 不同匹配阶数FrFT结果 |
| In the text | |
 |
图3 基于FrFT多普勒调频率估计的SAR处理流程 |
| In the text | |
 |
图4 仿真结果分析 |
| In the text | |
 |
图5 相位误差估计结果 |
| In the text | |
 |
图6 MAMD及本文方法在不同信噪比下估计的相位与真值偏差 |
| In the text | |
 |
图7 MD、MAMD及FrFT估计出的相位误差 |
| In the text | |
 |
图8 FRFT估计多普勒调频率成像结果 |
| In the text | |
 |
图9 A区图像不同方法处理结果 |
| In the text | |
 |
图10 B区图像不同方法处理结果 |
| In the text | |
 |
图11 P点FrFT结果 |
| In the text | |
 |
图12 MD、MAMD及FrFT方法P点方位PSLR对比 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


