EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 42 / No 5 (October 2024) JNWPU, 42 5 (2024) 875-881 Full HTML
Open Access
Issue
JNWPU
Volume 42, Number 5, October 2024
Page(s) 875 - 881
DOI https://doi.org/10.1051/jnwpu/20244250875
Published online 06 December 2024

© 2024 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

逆合成孔径雷达(inverse synthetic aperture radar, ISAR)的信号处理技术用于距离-多普勒域中移动目标的成像, 因其可对非合作机动目标成像, 自问世以来就成为人类对周围环境进行探测的重要工具[1–5]。目前, 对雷达高分辨率成像的需求迫切, 然而根据香农-奈奎斯特(Shannon-Nyquist)采样定理, 高分辨率的雷达成像需要较高的数据采样率, 遵循该采样定理直接对信号进行采样、处理和存储, 存在成本高、雷达系统设计难度大的问题。

在实际应用中, 由于外界环境或自身的影响, 雷达探测过程中存在大量的空时频稀疏采样现象。Donoho、Candes和Tao等提出了一个全新的利用信号稀疏性的信号采集、优化重构理论——压缩感知(compressed sensing, CS)。该理论指出, 当信号具有稀疏性或可压缩性时, 通过求解一个非线性最优化问题, 可以利用远小于香农-奈奎斯特采样定理的采样率准确或近似重建出原始的稀疏信号[6–8]。压缩感知理论一经提出, 就在医学图像、信息论、雷达成像、天文学、无线通信等领域受到高度关注。由于压缩感知只需要少量回波数据精确或近似精确地获取雷达的目标信息, 减少了数据采集、存储和传输量, 从而达到了简化雷达硬件设计, 提高系统分辨率的目的。

逆合成孔径雷达成像在多普勒域具有稀疏性, 因此压缩感知可以有效解决逆合成孔径雷达成像数据量大的问题, 基于压缩感知的逆合成孔径雷达成像算法是近些年非常热门的研究课题[9–12]。

1 模型

假设雷达信号x∈Cn在某个正交基或紧框架Ψ上是稀疏的, 即x=Ψα, 其中α具有稀疏性, 那么根据压缩感知理论, 信号x可以通过求解一个非线性优化问题从观测信号y∈Cm中准确或近似重建出来。观测信号

式中：Φ是与Ψ不相干的观测矩阵；α∈Cn为信号x在稀疏基Ψ下的稀疏表示；n∈Cn为观测过程中的噪声。令ΦΨ=Θ, Θ∈Cm×n(m < n)称为感知矩阵。根据观测信号y重建原始信号x是一个逆问题, 而线性方程(1)是欠定方程, 仅根据方程(1)不能重建出原始信号, 压缩感知理论利用稀疏性的先验信息对解空间进行约束来重建原始稀疏信号。

求解反问题(1)式的经典算法有贪婪算法和正则化方法。正交匹配追踪算法(orthogonal matching pursuit, OMP)[13]是一个经典的贪婪算法, 被广泛地应用于逆合成孔径雷达成像中。OMP算法通过最小化线性系统的残差来构造近似解或者解的支撑集, 该算法的优点是简单、易于理解且快速方便, 缺点是对噪声的影响较为敏感。正则化方法利用待重建信号的稀疏性信息对解空间进行约束, 正则化模型可以分为凸正则化模型和非凸正则化模型。ι1范数正则化是经典的凸正则化模型, 模型如下

式中：是数据拟合项；||α||1=是正则化项；λ>0是正则化参数。ι1范数正则化模型是一个凸优化问题[14–16], 并且具有产生稀疏解的能力[12–13]。ι1正则化模型被广泛用于逆合成孔径雷达成像[17–19], 该模型已有许多高效快速的求解算法, 例如交替乘子迭代算法(alternating direction method of multipliers, ADMM)[20]、迭代阈值收缩算法(iterative soft thresholding, IST)[21–22]和原始对偶算法(primal-dual algorithm)[23–24]等。

近些年, 大量研究表明凸正则化模型解的精确度不太高而且稀疏性也常常达不到预期, 而非凸正则化模型比凸正则化模型重建效果好[25–28], 例如文献[25]中提到, 在稀疏信号重建问题中非凸正则化模型可以使用比凸正则化模型更少的测量数据重建原始信号, 且重建出的精度更高。尽管非凸优化问题的求解很困难, 但是非凸正则化模型在逆合成孔径雷达成像中的应用仍然值得研究。

本文关注经典的非凸ιp(0 < p < 1)正则化模型, 并对该模型设计算法用于逆合成孔径雷达成像

式中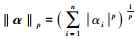，。对于ιp正则化模型, 本文提出了一个新的求解算法——迭代支撑集收缩算法。该算法基于MM迭代算法框架[29]提出, 并采用了支撑集收缩策略。在每步迭代中, 算法都有解析解, 因此该算法是一个单重循环算法, 效率比较高。数值实验表明该算法在逆合成孔径雷达成像中有很好的表现, 重建的图像质量很高。

2 算法

本节给出求解ιp正则化模型的迭代支撑集收缩算法的推导过程。该算法是在已有观测值和已知感知矩阵及观测噪声类型的情况下重构原始信号的过程。

优化问题(3)的目标函数是一个非凸、非利普希兹函数, 在设计算法时使用支撑集收缩策略[33]克服目标函数在零点的非利普希兹性。一般地, 对于一个向量α∈Cn, 定义它的支撑集为Ω(α)={i: |αi|≠0}。在实际计算中, 考虑到计算精度问题以及过小的元素参与计算会导致算法中权重过大, 因此当某个变量小于给定精度时, 在算法中也将该变量视为零。本文对于向量α, 定义它的ε-支撑集为

式中，[n]={1, 2, …, n}, ε是一个小的正数, 将Ω(αk)简记为Ωk。

支撑集收缩策略表明如果某个优化变量在某一步迭代中计算小于ε, 那么在后面的迭代中不再计算该变量, 它的值一直为零。引入支撑集收缩策略后, 在第(k+1)步需要求解如下的带约束优化问题

优化问题(4)中只需要考虑非零元的计算, 因此支撑集收缩策略不仅可以克服目标函数在零点的非利普希兹性还可以使每步迭代的规模减小, 使得算法效率更高。

MM迭代算法是优化领域的一个重要方法, 它的思想是通过极小化一系列目标函数在当前迭代点的替代函数来求解原问题。优化问题(4)仍然是一个非凸优化问题, 受MM算法的启发, 对(4)式中目标函数的正则化项在αk点做一阶泰勒展开逼近, 对数据拟合项在αk点做二阶泰勒展开逼近, 在每步迭代中, 通过极小化目标函数的逼近函数来获得当前迭代的解, 即在第(k+1)步求解如下的优化问题

式中，γ≥||ΘTΘ||2。优化问题(5)是一个强凸问题, 有唯一的解析解。

下面给出优化问题(5)的求解方法。通过合并同类项, 可得

式中, , c1为常数项。因此, 优化问题(5)的目标函数对每个指标i是可分的, 那么带约束优化问题(5)可以等价地写为

式中，。公式(6)中待求解的问题是一个软阈值收缩算子, 有如下解析解

综上, 给出迭代支撑集收缩算法:

算法1

输入: Θ, y, λ, γ, ε, α0, k: =1, δ, Kmax

1) 计算支撑集: Ωε(α)={i∈[n]: |αi|>ε}

2) 更新权重: wik=

3) 计算αk+1:

4) 如果相对误差或者k < Nmax, 则令k=k+1, 继续执行步骤1)~3);否则输出, 算法结束。

3 数值实验

将本文提出的迭代支撑集收缩算法用于二维逆合成孔径雷达成像中, 并且与OMP算法和求解正则化模型的IST算法进行对比。所有实验在同一台式机上完成, 台式机的配置为Windows 7, 64 bit, 8 GB memory, Intel Core(TM) i7-7700 CPU(3.60 GHz), 数学软件为MATLAB R2016a。仿真数据采用美国空军实验室V.C.CHEN提供的64×152维的米格-25战斗机数据, 雷达载频为9 GHz, 带宽为512 MHz, 脉冲重复频率为15 kHz, 雷达发射的信号形式为线性调频信号, 该回波数据已经完成了运动补偿, 可直接成像。

3.1 实验设置

实验中, 选取米格-25战斗机数据, 数据段大小为64×128, 其中行为方位向, 列为距离向, 用x=(x1, x2, …, x64), xi∈C128表示该数据段, 该数据段经过快速傅里叶变换(FFT)后，图像如图 1所示。

原始数据不含噪声, 为了验证算法在含有噪声的情况下也有良好的成像效果, 在构造观测信号y=(y1, y2, …, y64), yi∈C64的过程中加入随机高斯白噪声, 随机高斯白噪声符合标准正态分布。观测信号通过如下公式模拟得到

式中：Φ∈C64×128为观测矩阵；n为高斯白噪声, 观测信号y如图 2所示。

从观测数据的模拟过程可知, 观测信号比原始信号的数据量少了一半, 采集经过压缩后的观测信号然后通过该观测信号重构出原始信号而非直接采集原始信号可以大大减轻雷达硬件上的负担, 这也是压缩感知技术的意义。

已知雷达回波信号在多普勒域具有稀疏性, 因此选取正交傅里叶基Ψ∈C128×128为信号的稀疏基, Φ为随机高斯矩阵, 使得感知矩阵Θ=ΦΨ满足限制等距条件。算法的参数设置如下: γ=||ΘTΘ||22, ε=10-6, δ=10-5, Nmax=30, p=0.5, λ=2×105, 其中γ, ε, δ, Nmax是算法参数, p和λ是模型参数, 算法参数根据实验经验设置, p的取值对算法的影响下文会给出讨论, 正则化参数λ的值通过手动调试确定。

算法通过求解(3)式中的反问题得到稀疏信号α, 重建出的雷达信号x=Ψα, 通过对x做快速傅里叶变换(FFT)即可得到重建出的雷达图像, 将重建出的图像记为f。用图像的熵衡量重建图像的效果, 熵越小表示图像聚集程度越高, 重建效果越好, 熵越大表示图像越混乱, 重建效果越差。实验中，用MATLAB软件自带的“entropy”函数计算二维图像的熵。

thumbnail 图1

原始图像f成像结果
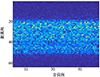thumbnail 图2

观测数据

3.2 逆合成孔径雷达成像

本节给出由迭代支撑集收缩算法重建得到的雷达图像, 如图 3所示。从图 3可以看出, 算法重建出的雷达图像质量很高, 没有旁瓣及不良点的影响。

thumbnail 图3

本文算法重建得到的雷达图像f成像结果

3.3 噪声对算法的影响

本节讨论噪声对本文算法的影响。在模拟观测信号时, 加入不同量级的高斯随机白噪声, 量级分别为0.1, 1, 10, 20, 50和100, 数值表示高斯随机白噪声的倍数, 高斯随机白噪声符合标准正态分布, 重建图像的熵如表 1所示, 图 4中给出了部分噪声下的雷达成像图。

从表 1和图 4可以看出, 噪声量级越大, 重建图像的熵越大, 图像效果越差。

表1

本文算法在不同量级(倍)噪声下重建图像熵的对比

thumbnail 图4

本文算法在不同量级的噪声下重建图像

3.4 p值对算法的影响

本节讨论p值对算法的影响。实验中, 令p分别取0.1, 0.3, 0.5, 0.7, 0.9, 当算法取不同的p值时, 参数λ的值也不同, 在p取不同值时算法重建图像的熵如表 2所示。

从表 2可以看出, p取不同值时, 算法重建图像的熵差别不大, 重建图像的效果都比较好, 这说明了本文提出的算法对p的取值是鲁棒的。

表2

本文算法在p取不同值下重建图像的熵对比

3.5 算法对比

本小将本文提出的迭代支撑集收缩算法与一些经典的逆合成孔径雷达成像算法进行比较, 包括贪婪类算法OMP算法和求解正则化的IST算法。测试了2种感知矩阵, 分别为随机高斯矩阵和随机贝努利矩阵, 雷达成像结果如图 5所示, 重建图像的熵与CPU耗时如表 3~4所示。

从图 5可以看出本文算法重建出的雷达图像最清晰, 几乎没有不良点, 成像效果好于IST算法, 而IST算法的成像效果好于OMP算法。表 3中由本文算法重建图像的熵也最小, 熵越小表明图像越清晰。

在CPU耗时上, 从表 4可以看出本文算法比IST算法耗时少, 这是因为本文算法每次迭代待求解的问题规模在减小, OMP算法耗时最少。

从本节实验可以看出, 迭代支撑集收缩算法是一个简单高效、易于实现并且成像效果好的算法。以往经常用“复杂”、“对参数敏感”等词语来描述非凸算法, 而本文提出的算法简单高效, 并且该算法只需要调试一个正则化参数λ, 在p取0.5时, 该参数取100 000~250 000算法都有比较好的成像效果。

thumbnail 图5

本文算法、IST算法和OMP算法的重建图像
表3

不同算法重建图像的熵对比

表4

不同算法重建图像的CPU耗时对比 s

4 结论

本文对压缩感知领域中一个经典的非凸ιp正则化模型提出了一个新的求解算法——迭代支撑集收缩算法, 并将该算法应用于逆合成孔径雷达成像中。迭代支撑集收缩算法简单高效, 打破了以往大家对非凸类算法复杂、对参数敏感的印象, 数值实验表明该算法比经典的OMP算法和IST算法成像更清晰。迭代支撑集收缩算法是一个求解非凸模型的算法, 因此该算法的收敛性分析是一个比较难的问题, KL理论[34]的提出使得分析非凸算法的收敛性成为可能, 后续会对该算法的收敛性问题进行分析。

References

  1. BAO Zheng, XING Mengdao, WANG Tong. Radar imaging technology[J]. Beijing: Publishing House of Electronic Industry, 2005 (in Chinese) [Google Scholar]
  2. LU Baoguo, LIANG Bo, MA Huanfang. Method for aircraft target recognition and classification in optical remote sensing image[J]. Command Information System and Technology, 2020, 11(5): 78–82 (in Chinese) [Google Scholar]
  3. XU Ying, GU Yu, PENG Dongliang. SAR image recognition based on sparse representation and multi-feature fusion[J]. Command Information System and Technology, 2020, 11(3): 29–35 (in Chinese) [Google Scholar]
  4. GUILLAUME H, RENE G. High resolution snapshot SAR/ISAR imaging of ship targets at sea[J]. SPIE Remote Sensing, 2003, 488339–47 [Google Scholar]
  5. LAZAROV A, MINCHEV C N. ISAR image reconstruction and autofocusing procedure over phase modulated signals[J]. Radar, 2002, 490: 536–541 [Google Scholar]
  6. DONOHO D L. Compressed sensing[J]. IEEE Trans on Information Theory, 2006, 52(4): 1289–1306 [Article] [CrossRef] [Google Scholar]
  7. CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans on Information Theory, 2006, 52(2): 489–509 [Article] [CrossRef] [Google Scholar]
  8. CANDES E J, ROMBERG J K, TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207–1223 [Article] [CrossRef] [Google Scholar]
  9. WEHNER D R. High-resolution radar[M]. 2nd ed. Boston, MA: Artech House, Inc, 1994 [Google Scholar]
  10. BARANIUK R, STEEGHS P. Compressive radar imaging[C]//The 2007 IEEE Radar Conference, 2007: 128-133 [Google Scholar]
  11. POTTER L C, PARKER J T. Sparsity and compressed sensing in radar imaging[J]. Proceedings of the IEEE, 2010, 98(6): 1006–1020 [Article] [CrossRef] [Google Scholar]
  12. PATEL V M, EASLEY G R, HEALY D M. Compressed synthetic aperture radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 244–254 [Article] [NASA ADS] [CrossRef] [Google Scholar]
  13. TROPP J A. Greed is good: algorithmic results for sparse approximation[J]. IEEE Trans on Information Theory, 2004, 50(10): 2231–2242 [Article] [CrossRef] [Google Scholar]
  14. DAUBECHIES I, TESCHKE G, VESE L A. Iteratively solving linear inverse problems under general convex constraints[J]. Inverse Problems and Imaging, 2007, 1(1): 29–46 [Article] [CrossRef] [Google Scholar]
  15. DONOHO D L. For most large underdetermined systems of linear equations the minimal l1-norm solution is also the sparsest solution[J]. Communications on Pure and Applied Mathematics, 2006, 59(6): 797–829 [Article] [CrossRef] [MathSciNet] [Google Scholar]
  16. BOYD S, VANDENBERGHE L. Convex optimization[J]. Cambridge: Cambridge University Press, 2004 [CrossRef] [Google Scholar]
  17. ZHANG L, QIAO Z J, XING M D. High-resolution isar imaging by exploiting sparse apertures[J]. IEEE Trans on Antennas and Propagation, 2012, 60(2): 997–1008 [Article] [NASA ADS] [CrossRef] [Google Scholar]
  18. ZHANG L, QIAO Z J, XING M D. High-resolution ISAR imaging with sparse stepped-frequency waveforms[J]. IEEE Trans on Geoscience and Remote Sensing, 2011, 49(11): 4630–4651 [Article] [NASA ADS] [CrossRef] [Google Scholar]
  19. ZHANG L, XING MD, QIU C W. Achieving higher resolution ISAR imaging with limited pulses via compressed sampling[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 567–571 [Article] [CrossRef] [Google Scholar]
  20. BOYD S, PARIKH N, CHU Eet al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3(1): 1–122 [Google Scholar]
  21. CHAMBOLLE A, VORE D E, NAM-YONG R Aet al. Nonlinear wavelet image processing: variational problems, compression, and noise removal through wavelet shrinkage[J]. IEEE Trans on Image Processing, 1998, 7(3): 319–335 [Article] [CrossRef] [Google Scholar]
  22. DAUBECHIES Ingridj, DEFRISE Michel, DEMOL Christine. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413–1457 [Article] [CrossRef] [Google Scholar]
  23. CHAMBOLLE A, POCK T. A first-order primal-dual algorithm for convex problems with applications to imaging[J]. Journal of Mathematical Imaging and Vision, 2011, 40(1): 120–145 [Article] [NASA ADS] [CrossRef] [Google Scholar]
  24. ESSER E, ZHANG X, CHAN T F. A general framework for a class of first order primal-dual algorithms for convex optimization in imaging science[J]. SIAM Journal on Imaging Sciences, 2010, 3(4): 1015–1046 [Article] [CrossRef] [Google Scholar]
  25. CANDES E J, WAKIN M B, BOYD S P. Enhancing sparsity by reweighted l1 minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 877–905 [CrossRef] [Google Scholar]
  26. CHARTRAND R, STANEVA V. Restricted isometry properties and nonconvex compressive sensing[J]. Inverse Problems, 2008, 24(3): 035020 [Article] [CrossRef] [Google Scholar]
  27. FOUCART S, LAI M J. Sparsest solutions of underdetermined linear systems via lq-minimization for 0 < q < 1[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 395–407 [CrossRef] [Google Scholar]
  28. SUN Q. Recovery of sparsest signals via lq-minimization[J]. Applied and Computational Harmonic Analysis, 2012, 32(3): 329–341 [Article] [CrossRef] [Google Scholar]
  29. FIGUEIREDO M A T, BIOUCAS-DIAS J M, NOWAK R D. Majorization-minimization algorithms for wavelet-based image restoration[J]. IEEE Trans on Image Processing, 2007, 16(12): 2980–2991 [CrossRef] [Google Scholar]

All Tables

表1

本文算法在不同量级(倍)噪声下重建图像熵的对比

In the text
表2

本文算法在p取不同值下重建图像的熵对比

In the text
表3

不同算法重建图像的熵对比

In the text
表4

不同算法重建图像的CPU耗时对比 s

In the text

All Figures

thumbnail 图1

原始图像f成像结果
In the text
thumbnail 图2

观测数据
In the text
thumbnail 图3

本文算法重建得到的雷达图像f成像结果
In the text
thumbnail 图4

本文算法在不同量级的噪声下重建图像
In the text
thumbnail 图5

本文算法、IST算法和OMP算法的重建图像
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.